基于GO-FLOW的列控车载系统可靠性分析

李少雄， 齐金平，3， 周亚辉， 王 康

（1.兰州交通大学机电技术研究所，兰州730070；2.甘肃省物流及运输装备信息化工程技术研究中心，兰州730070；3.甘肃省物流与运输装备行业技术中心，兰州730070）

0 引 言

车载系统作为动车组列控系统的重要组成部分，担负着接受地面信号以及向车站传输列车状态的任务，其一旦发生故障，不仅会造成整条线路运输紊乱，还会直接危及乘客安全和造成重大经济损失［1-2］。实际运营途中，车载系统各部件相互协作，保证系统的高可靠性和可用性［3］。由于系统结构复杂，部件类型繁杂，故障组合表现为典型的多状态系统，同时，在维修途中为了保证系统的工作效率，应限定维修工数量和维修优先权。

GO-FLOW方法是一种以成功为导向的、有效的系统可靠性分析方法［4］，能够避免传统的故障树、Markov等方法在分析时存在状态数会随着系统规模的不同出现爆炸性问题［5］。文献［6］中提出了可修系统部件维修率的等效模型，并且在冗余泵单元中验证了所提出模型的有效性和可行性。文献［7］中将布尔代数引入GF模型可靠性分析中，解决了GF模型中存在循环的反馈环，并且将GF模型可靠性分析结果与GO法结果相比较，验证GF法的可行性。文献［8］中在GF模型定量分析时，采用降阶法对共有信号进行修正，选取适当的时间间隔观察可靠度随时间的变化趋势。文献［9］中在高速铁路接触网GF模型中考虑了部件失效率随时间的变化，使得GF模型计算多时序、多状态系统的结果更接近于实际运行情况。文献［10］中的GF模型中，在性能分析时结合共因失效和系统的冗余性，提出了可修系统的定量计算方法，利用定性或定量GF运算得到系统的可靠性分析结果。文献［11］中提出了多状态可修系统的GO法定量计算公式，并将故障率分析结果与故障树模型分析结果对比。以上对系统或部件的故障分析方法并未同时考虑到复杂冗余系统的故障组成多状态性和部件可维修性两方面的因素。

本文为了避免高速列车可靠性分析领域GOFLOW方法仅用于定量分析不可维修系统的应用局限，通过改进操作符功能后用于可维修系统，并结合可维修系统多状态概率计算模型，在定量分析多状态可维修复杂冗余系统的问题上对GO-FLOW方法的应用进行了扩展。以高速列车车载系统可靠性分析模型为例，对所建模型进行验证和分析，相比于GO模型，GOFLOW法更侧重对信号流的模拟和系统动态特性的反映。

1 可维修系统

1.1 可维修系统状态

假设某系统包括M个可维修单元，则其有M+1个状态，各状态表示如表1所示［12-14］。

表1 可维修系统状态图

1.2 可维修部件可靠性等效模型

可维修系统中串联结构较多，设有M个单元的串联结构（见图1），每个单元的可靠性特征量为

图1 串联结构GO图

当M个单元完全独立时，串联结构的成功概率是所有单元成功概率的乘积，串联结构的等效故障率是所有单元故障率之和，计算式为

并联结构可以包含停工相关、维修相关和备用相关等相关性，先得确定单元总数M、成功数K、停工故障数I、维修工数L和备用指示J等参数：

状态转移率

各状态概率

工作概率

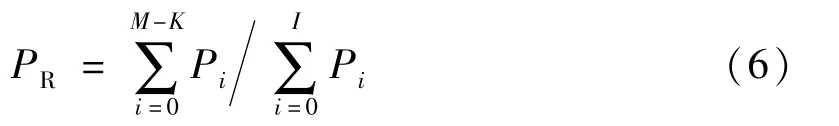
计算的等效故障率和等效维修率分别为：

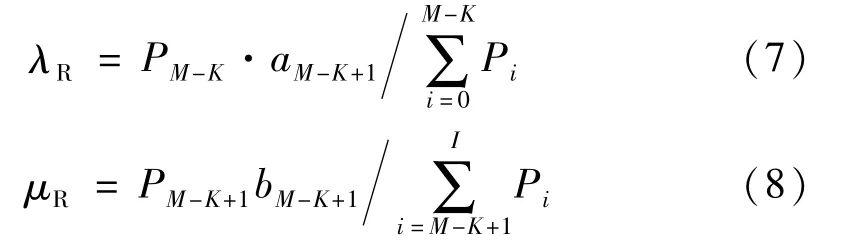
1.3 考虑维修的操作符运算规则

考虑维修的操作符运算采用如图2所示的组合模型。进行系统状态概率分析时，将n1和n2操作符作为整体模块。

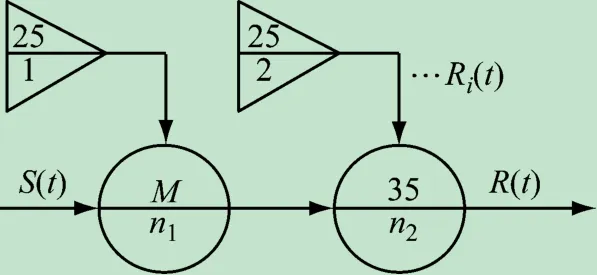
图2 可维修系统GO-FLOW组合模型

将类型35操作符用于描述某类可维修部件的组合模型，并且μ≠0，对应算法为

将图2中的35操作符分别用考虑维修的37和38操作符代替，组合运算式分别为：

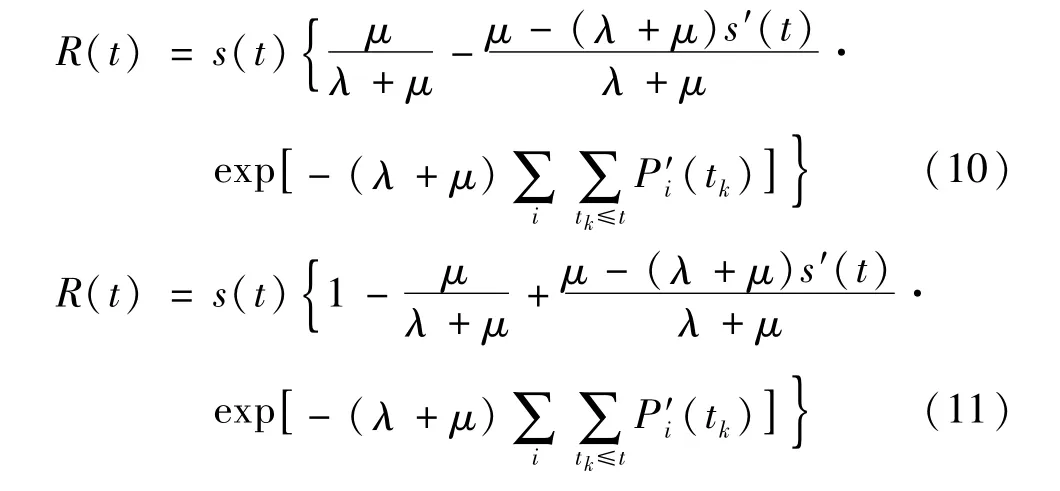
2 多状态可维修系统GO-FLOW模型

2.1 可维修部件可靠性参数等效模型

以3个部件组建的可维修系统为例，假定有1个维修工并且维修优先权1＞2＞3，则各部件的状态方程为［15］：

部件2的等效维修率μ′2=μ2P1（t），是时间的变量，但GO-FLOW法只能处理失效率和维修率是常数的情况，因此将部件2的维修率近似等效为

同理可得：

为了让模型的适用性更加普遍，推广到任意m部件n（n≤m）个维修工的系统，并且各部件的维修优先权1＞2＞…＞m，总结出部件i的状态方程为

其中：

式中：Prob，i为维修优先权在部件i之前的所有部件中有k（0＜k＜i）个发生故障，i-1-k个正常工作的概率。

与3个部件一个维修工的计算模型相比较，得到部件i等效维修率的一般表达式：

2.2 多状态可维修系统参数模型

通过实际考察，对检修故障重叠的情况进行修正，需防止因检修扩大系统已发生故障范围。如在两设备叠加系统中［16］，应除去一设备处于故障和检修状态时将另一设备退出运行状态进行检修的情况。因此两设备存在：F+N；F+F；M+N和M+F（故障：F，正常：N，检修：M）4种情况。

多部件系统中，考虑F+N和F+F两种系统状态，除系统部件j外，其余部件处于正常或故障状态的概率为

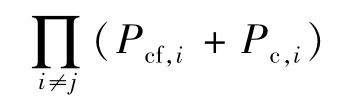
则由部件j故障引发的系统故障率为

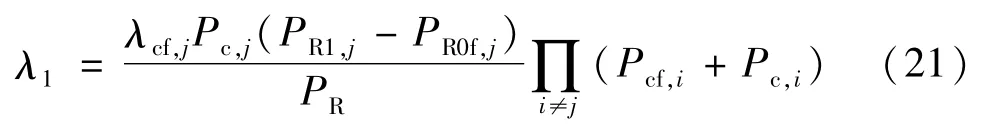
类似地，考虑M+N和M+F两种系统状态，由部件j故障引发的系统故障率为

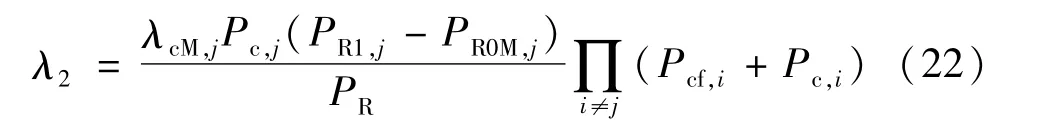
推理得多状态可修系统故障率为

3 案例分析

3.1 车载系统的结构并建立GO-FLOW模型

以列控系统车载子系统为例，限制维修工的数量和维修优先权的情况下使用GO-FLOW法进行可靠性分析，车载系统结构图如图3所示。

图3 CTCS-3级列控车载系统结构示意图

通过对车载子系统内部设备互相之间关系的分析，考虑部件可维修以及故障数据的模糊性的情况下建立车载系统的GO-FLOW模型，如图4所示。

图4 车载系统GO-FLOW模型

车载子系统GO-FLOW可靠性分析模型分别包括24个信号流和操作符，代表含义如表2所示。

表2 车载子系统GO-FLOW模型各操作符含义

3.2 可靠性分析

根据车载系统的工作原理与各部件间的逻辑关系，在GO-FLOW模型分析车载系统的可靠性型时，将整个工作过程划分为7个时间点，如表3所示。

表3 时间段划分

综合定量计算模型，分别计算操作符在7个时间点的输出信号强度，结果统计如表4所示。

表4 车载子系统GO-FLOW模型各操作符信号强度

3.3 系统仿真

取总时长t=1 500 h，以Δt=500 h为采样时间，初始输出信号强度O（0）=1，利用Matlab进行仿真分析，分别得到了GO模型和GF模型对车载系统的输出信号强度分析结果如图5所示。

图5 GO模型数值解与GO-FLOW法计算结果

由图5可知，采用GO-FLOW模型计算的系统输出信号强度略小于GO模型的分析结果，两者相对误差的最大结果仅为0.9%，并且GF模型在t=0～100 h仿真的结果与定量计算结果一致，可见GO-FLOW模型更能反映系统实际分析的精度要求。

4 结 语

将GO-FLOW模型用于多状态可维修系统中，并且限制维修工的数量和各部件间的维修优先权，从3个部件1名维修工组建的可维修系统出发，推导出多个部件多个维修工的可修系统可靠性计算模型。

以CTCS-3级列控车载系统为例，建立多状态可修系统的GF模型，结合系统工作原理，找出0～100 h工作过程中的7个关键时间点，定量分析各时间点操作符的输出信号强度。利用Matlab分别对GF与GO模型的定量分析结果进行仿真，得到了0～1 500 h车载系统可靠度的变化曲线，在0～500 h过程中系统的可靠度下降猛烈，1 500 h时系统的输出信号强度接近于0；并且系统工作在0～100 h的过程中，GF模型的仿真结果与定量计算结果相一致。验证了对多状态可修系统进行可靠性分析的GF模型是有效可行的，并且计算结果更加精准，使得GO-FLOW模型用于分析系统可靠性的能力得到进一步提升。

通过整理兰新客专2018年CTCS-3级列控车载系统现场维护数据，验证了分析结果准确性和有效性。