从概率论的发展史谈数学期望
潘小峰 胡 坤 (江苏省外国语学校 215104)
1 概率论的发展史和数学期望的最早提出
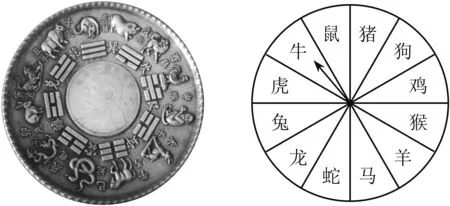
概率论是一门研究随机现象规律的数学分支.概率论起源于17世纪中叶,当时一个关于赌博的问题促使数学家们率先思考概率论的问题.数学家费马向另外一位著名数学家帕斯卡提出这样的一个问题:“两个赌徒做了一个赌局,规定谁先赢z局谁就胜利,当赌徒X赢x局(x 要想理解数学期望这一概念,我们先来看一个问题:甲乙两学生学期末考试成绩分别如表1、表2,请问哪个学生的学习成绩好? 表1 表2 可以发现这两位学生的总分是一样的,如果计算平均分,平均成绩也是一样的,所以说两位学生的学习水平应该是一样的.但是如果加入限定条件“在这个年级中,每周语文有10节课,数学有8节课,而生物只有2节课”,该如何计算才能更加合理?这个时候以平均成绩进行评价是没有考虑到这三个科目的相对重要性的,而评价学生成绩时,这个因素不能不考虑,因此我们用下面的方法来计算平均成绩似乎更合理些: 初中学习的普通平均是加权平均的一种特例,这时所有的权相等.平均值按其大小总在原始数据当中,因此它反映了一组数据的中心趋势(central tendency). 日常生活中我们也经常会遇见一些用到数学期望的案例.例如集会上的转盘游戏,若将圆盘分为十二等份,每份代表一个生肖,顾客任选一个生肖,旋转转盘,转到所选生肖,以1比10得到赏金,不中者其押金归店家(图1). 图1 为了对这种游戏有实质性的了解,最好考察一个玩家当他押上1元之后的期望所得,显然其分布列为: 现在的福利彩票3D是由百位、十位、个位三个数字组成一注.个、十、百三位上分别从0-9中任意选择一个号码组成一个三位数进行投注.中奖规则分为三种:(1)单选:投注号码与开奖号码完全相同且排列顺序一致,就中奖,每注1 000元;(2)组选三:开奖号码中必须有两位是相同的数字,投注号码与开奖号码相同,顺序不限,就中奖,每注320元;(3)组选六:投注号码与开奖号码相同,顺序不限,就中奖,每注160元. 上述关于游戏和彩票的讨论集中于分析未来不确定事情的后果,体现了数学期望概念的重要性,普及概率知识有助于杜绝赌博现象.其实概率论的发展史也说明了理论与实际之间的密切关系,许多研究方向的提出归根到底是有其实际背景的,反过来,当这些方向被深入研究后,又可指导实践,进一步扩大和深化应用范围.2 以一个成绩分析问题直观理解数学期望

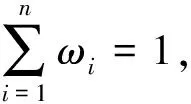
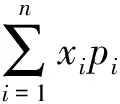
3 利用数学期望认清生活中的博弈现象

4 结语

