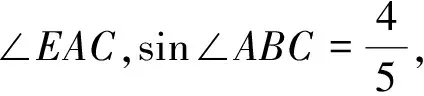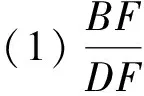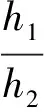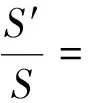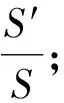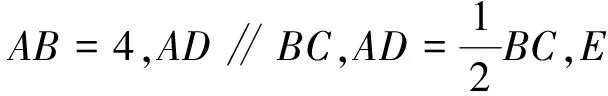一道苏州中考数学压轴题的分析与思考

柳月明 (江苏省苏州市吴中区木渎实验中学 215100)

2020年苏州市中考数学压轴题(第28题，满分10分)是一道动态型综合题，涉及的图形有三角形、四边形、圆，涉及的知识点有相似、全等、二次函数、勾股定理等，涉及的方法有面积割补、函数建模、以静制动等．此题源于课本的习题，又加入圆进行了变化创新，让学生觉得似曾相识，同时又有变化和深化，可见命题者独具匠心，是一道受到师生普遍称赞的好题．

1 原题呈现

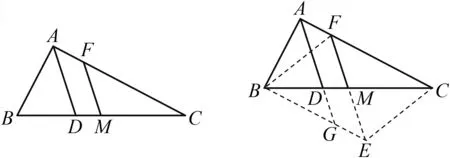
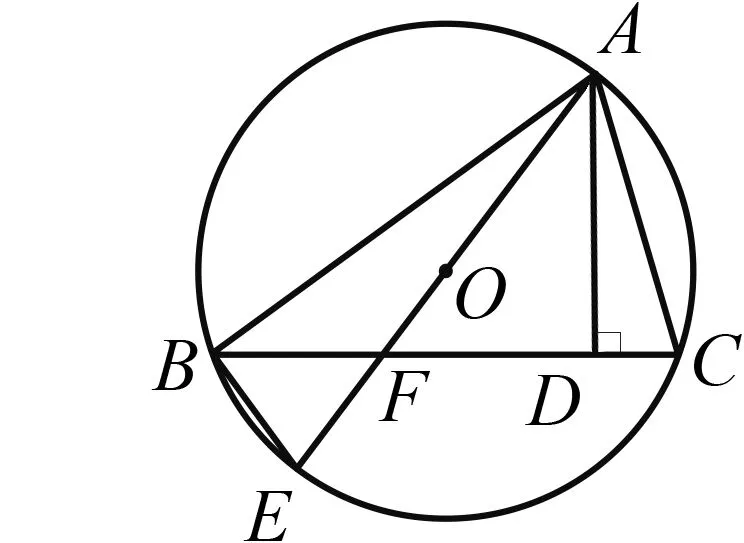
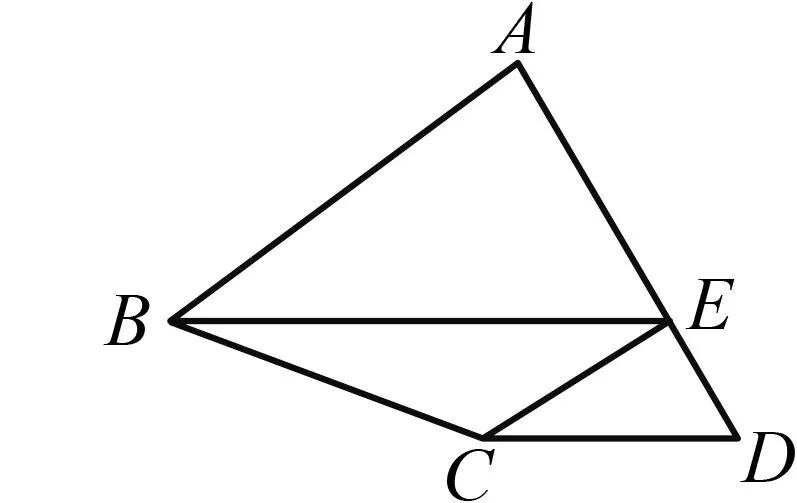
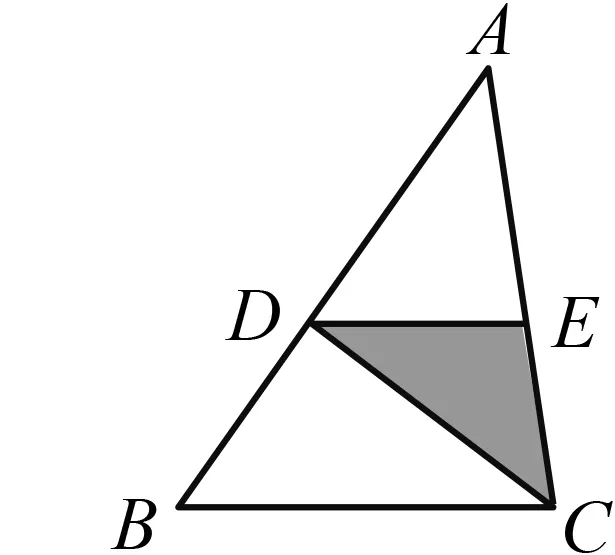
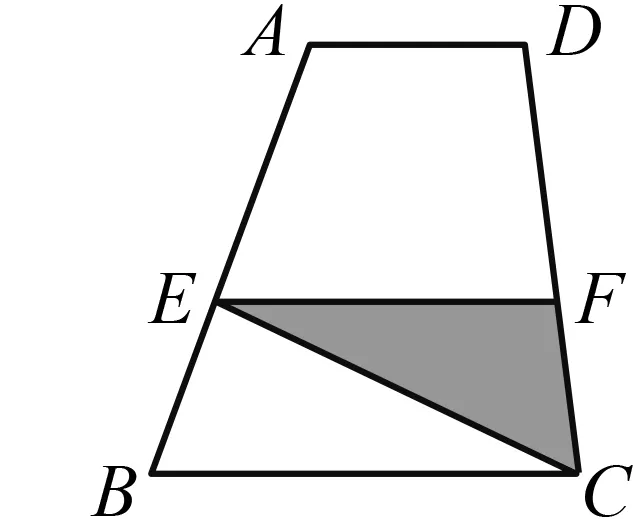
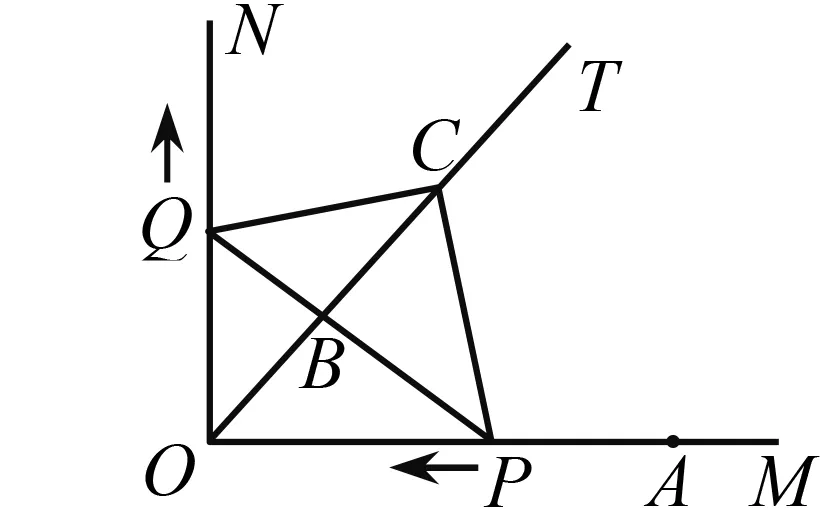
如图1，已知∠MON=90°，OT是∠MON的平分线，A是射线OM上一点，OA=8 cm．动点P从点A出发，以1 cm/s的速度沿AO水平向左作匀速运动，与此同时，动点Q从点O出发，也以1 cm/s的速度沿ON竖直向上作匀速运动．连结PQ，交OT于点B．经过O,P,Q三点作圆，交OT于点C，连结PC,QC．设运动时间为ts，其中0

图1

(1)求OP+OQ的值．

(2)是否存在实数t，使得线段OB的长度最大？若存在，求出t的值；若不存在，说明理由．

(3)求四边形OPCQ的面积．

2 似曾相识，意料之中

通过和课本中习题的对比，发现此中考题主要是由课本习题改编而来．

2.1 题目来自于课本

如图2，如果去掉圆的部分，就能发现该题来源于课本的三个地方：

图2

苏科版七下《证明》一章中的实验：画∠AOB=90°并画∠AOB的平分线OC．(1)把三角尺的直角顶点P落在OC的任意一点上，并使三角尺的两条直角边分别与OA,OB垂直，垂足分别为E,F(图3)．度量PE,PF的长度，这两条线段相等吗？(2)把三角尺绕点P旋转，三角尺的两条直角边分别交OA,OB于点E,F(图4)，PE,PF相等吗？

图3 图4 图5

苏科版八上第二章“2.4线段、角的轴对称”中的习题2.4第11题：七年级通过实验可以得到PE=PF的结论，现在请你证明这个结论．

苏科版八上第二章“2.5等腰三角形的轴对称”中的习题2.5第12题：如图5，在△ABC中，

∠ACB=90°，AC=BC，D是AB的中点，点E在AC上，点F在BC上，且AE=CF．求证：DE⊥DF．可以发现，图2与上述教材中的图3—5基本类似．

2.2 方法来自于平常

第(1)问，连结AC，通过证明△CQO≌△CPA即可得OP+OQ=OA=8 cm．而三角形全等是证明线段相等并将线段进行转化的常规方法．

第(2)问，用含t的代数式表示OB，建立二次函数的模型，用二次函数的最值来求解．这也是一种常规的方法．

第(3)问，方法一，把四边形分割成两个三角形△OPQ,△CPQ，即可求解．方法二，由△CQO≌△CPA，把四边形转化成三角形△CAO．这些转化方法是常用的求面积的方法．

2.3 变化来自于课标

义务教育数学课程标准指出，在数学课程中，应当注重发展学生的几何直观、推理能力和模型思想．本题第(1)题就是考查学生的几何直观能力，根据图形和已知条件直观发现OP+OQ的长度是一个定值．本题的第(3)题也是考查学生的几何直观能力，通过分割发现四边形的面积是个定值．本题第(2)题通过构造二次函数模型，解决变化中的最值问题．

3 精彩在改变中

研究此中考题，发现命题者经过思考进行了适当的变化，主要突出能力的考查．

改变1 变旋转为动点．把三角尺的旋转改为两条边上各有一个动点，通过适当的变化，来考查学生的应变能力．

改变2 改直接证明线段相等为求OP+OQ的值．在问题设问上进行了变化，加深了难度，进一步考查学生的应变能力．

改变3 加入圆．这是本题的一大亮点．加入圆后，图形变得复杂了，圆中的知识可以综合利用起来，更能考验学生的综合应用能力．

改变4 加入二次函数．二次函数是初中数学的重点，也是难点，需要学生有较强的思考能力.在这里的变化中加入二次函数，可谓合理恰当，增加一定难度，从而考查学生深入思考的能力．

4 中考复习建议

对该中考综合题的研究分析启示我们：在应对中考复习时除了要注重基础知识、基本图形、基本方法，还要在此基础之上进行适当的变化，才能驾驭中考中的较难题．

4.1 以教材为本

既然题目来自于课本，就要立足课本．一是把课本上的题目弄清楚、想明白．弄清楚题目的条件和结论，想明白解题的方法和解题时涉及的数学知识点，熟悉题目的图形和图形所隐含的信息．

4.2 以常规方法为要

数学方法有很多，但要注重常规方法的训练和掌握，比如分析与综合、化归、建模、分类讨论、数形结合等．在平时的教学中要突出方法，在解题结束后要注意归纳方法、反思方法，做到真正掌握方法，形成有法可依的解题规律．

4.3 以深化为策

因为是面对中考，而中考中不会碰到一模一样的题，尤其是中考的较难题，所以变化是常态的．但是变化不是凭空发生的，常常有其背景和原来的模型，而背景或模型基本来源于教材，因此要基于教材进行深化．

·图形深化

比如从三角形变到四边形．三角形的中线、角平分线都是最基本的知识，但是三角形的中线倍长之后就能和平行四边形联系起来，这种变换是很巧妙的，也能使问题更加深入．例如，如图6，△ABC中，AB=4,AC=7，M是BC的中点，AD平分∠BAC，过M作MF∥AD，交AC于点F．求FC的长．

图6 图7

如图7，倍长FM后构造了FBEC和AGEF，得FC=BE,AF=GE，FC=AC-AF=7-AF①，BE=BG+EG=BA+EG=4+GE②．联立①②解方程组得AF=GE=1.5,FC=5.5．

·条件结论深化

图8

把等高三角形的面积比转化到了底之比，利用了等腰三角形知识和相似三角形对应边成比例的性质，加大了难度，深化了问题，可以通过这样的训练提高学生的解题能力．

·问题深化

图9

·小题组合

综合题顾名思义就是由许多元素综合起来组成的题目，这些元素是基本知识点、基本图形、基本方法，因此平时注意对一些课本小题目的研究，找到联系，有机组合，就可以编成综合题，训练学生的综合运用能力．

图10

图11

这两题有较多共同之处，知识点上都用到三角形相似的判断及性质和三角形面积计算方法．复习题21题进一步加入了函数关系式及二次函数的最值，难度随之加大．图形方面还是在三角形、四边形上面展开．方法上还是常规的求面积就作高，复习题21题第(3)小题通过二次函数最值探索大小关系，是比较新颖的方法．

当我们把这两道题组合起来看，可以发现苏州市2018年中考第27题就来源于这两题．

(苏州2018中考27题)如图12，在△ABC中，AB=4，D是AB上一点(不与A,B重合)，DE∥BC，交AC于点E，连结CD，设△ABC的面积为S，△DEC的面积为S′．

图12

图13

此题的第(1)(2)问研究了三角形的面积，涉及到相似三角形的性质，与上面的课本习题非常相像；第(3)问从三角形拓展到四边形，是对问题的进一步深化，较好地考查了学生的应变能力．

年年中考年年考，中考题目年年变，但变是基于课本、基于课程标准的，所谓百变不离其宗．因此，我们只要立足课标、研透教材，善于在课本原有题目上进行条件的变化、结论的变化、图形的变化、方法的变化，就能改编出好的题目供学生思考训练，从而提高解题能力．