基于WAEEMD和MSB的滚动轴承故障特征提取

郭俊超 甄 冬 孟召宗 师占群 谷丰收

1.河北工业大学机械工程学院，天津，300130 2.Centre for Efficiency and Performance Engineering,University of Huddersfield,Huddersfield，UK，HD1 3DH

0 引言

滚动轴承是旋转机械中使用最广泛的零部件之一，其运行状态是否正常直接影响整个机器系统的效率和性能[1]。如果没有预警，轴承故障将导致经济损失和严重的安全问题，因此，滚动轴承的失效预警对于确保机械系统的正常运行是必不可少的，近年来轴承故障诊断受到了越来越多的关注[2-3]。目前，许多先进的信号处理方法已被应用于滚动轴承的故障诊断，包括维格纳-威利分布(Wigner-Ville Distribution，WVD)、经验小波变换(empirical wavelet transform，EWT)、局部均值分解(local mean decomposition，LMD)和变分模态分解(variational mode decomposition，VMD)等。尽管这些方法已经被证明对于滚动轴承故障检测是有效的，但它们各自存在着一些局限性。例如，WVD具有较高的时频分辨率，但会受到交叉项干扰的限制[4]；EWT是一种出色的信号分解方法，但是它受到二进制频带分配的困扰[5]；LMD是一种用于非平稳信号的自适应分析方法，但它受模态混叠的影响[6]。VMD是一种自适应的准正交信号分解方法，但是很难确定其惩罚因子和分解层数[7]。此外，还有多种其他信号处理方法可用于滚动轴承的故障诊断[8-9]，但是这些方法中的大多数主要关注信噪比的提高，而忽略了振动信号中固有的调制特性。

近年来，调制信号双谱(modulation signal bispectrum，MSB)分析在故障诊断领域得到应用。该方法能够有效地利用调制特性且具有高性能的噪声抑制能力，此外，它还具有保留相位信息的能力。GU等[10]利用MSB诊断电动机的转子故障，并通过仿真和实验数据证实了该方法优于常规双谱分析方法。ZHANG等[11]提出使用MSB来监控齿轮磨损恶化的程度。TIAN等[12]开发了一种新颖的MSB检测器，在仿真和实验故障检测中该检测器比快速谱峭度(fast kurtogram，FK)更精确、更可靠。但是，这些研究工作假定振动信号是平稳的，因此在提取故障特征时可能会产生干扰频率分量，从而影响故障诊断的精度。

集合经验模态分解(ensemble empirical mode decomposition，EEMD)是由WU[13]提出的一种先进的非线性和非平稳信号处理方法，在故障检测中得到广泛应用[14-16]，但是如何选择最具敏感性的固有模态函数(intrinsic mode functions，IMF)仍然是一个棘手的问题。目前，已有文献报道了一些关于选择敏感的IMF的分析方法[17-20]。这些方法在选取敏感的IMF方面是有效的，但是它们没有考虑脉冲信号幅值和瞬时频率的变化，而这可能会影响故障诊断的准确性。为了解决这一问题，DENG等[21]提出使用Teager能量峭度(teager energy kurtosis，TEK)选择敏感IMF，该方法的有效性已得到证明[22]。

本文提出一种基于加权平均集合经验模态分解(weighted average ensemble empirical mode decomposition，WAEEMD)和MSB的滚动轴承故障特征提取方法。实验对比分析结果表明，WAEEMD-MSB方法在滚动轴承故障特征提取方面的性能优于快速谱峭度(FK)和EEMD-MSB方法。

1 调制信号双谱分析

1.1 MSB

MSB是一种基于常规双谱的先进解调方法[10]，它通过抑制随机噪声和干扰分量来解调振动信号中固有的调制成分。对于离散时间信号x(t)进行相应的离散傅里叶变换X(f)，MSB在频域中表示为[11]

BMS(fc,fx)=E〈X(fc+fx)X(fc-

fx)X*(fc)X*(fc)〉

(1)

式中，BMS(fc,fx)、E〈·〉分别为信号x(t)的调制信号双谱和期望算子；fc、fx分别为载波频率和调制频率；(fc+fx)、(fc-fx)分别为较高和较低的边带频率。

MSB总相位定义为

φMS(fc,fx)=φ(fc+fx)+φ(fc-fx)-

φ(fc)-φ(fc)

(2)

当fc和fx耦合时，它们的相位表示为

(3)

将式(3)代入式(2)，可以得出MSB总相位为零，并且其幅值将由四个分量幅值的乘积所确定,因此，在频率(fc,fx)处出现双谱峰值。此外，如果随机噪声分量没有耦合而是随机分布，则MSB的幅值大小接近零。这样，MSB可以有效地抑制振动信号中的随机噪声和干扰分量，从而更清楚地揭示与调制效果有关的成分。

为了更精确地量化边带幅值，通过使用幅值归一化消除fc的影响来改善MSB。为将这种改进与MSB区别开来，定义MSB边带估计器(MSB sideband estimator，MSB-SE)如下[12]：

(4)

其中，BMS(fc,0)为fx=0时的功率谱平方估计，其MSB-SE的典型分析结果如图1所示。

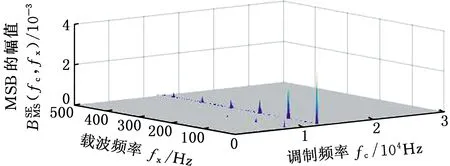
图1 MSB-SE的分析结果

1.2 MSB检测器

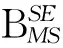
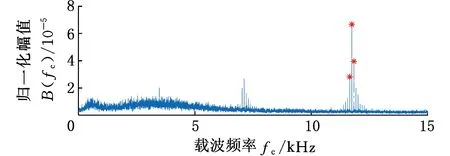
图2 MSB的切片的结果

(5)

式中，Δf为fx方向的频率分辨率。

为了获得更可靠的结果，采用图2中标有“*”的几个MSB切片的平均值来进一步得出MSB检测器，其表达式为

(6)

其中，N为所选切片的总数(在图2的情况下切片数为3)，该值取决于MSB的峰值。

MSB检测器如图3所示。

图3 MSB检测器的结果

2 加权平均集合经验模式分解

EEMD是一种非平稳、非线性信号的自适应分解方法[13]。该方法自适应地将复杂的振动信号分解为一系列不同频带的IMF。

(7)

式中，y(t)为测量信号；ci(i=1,2,…,G)为第i个IMF；G为IMF的数目。

为了避免丢失有用的故障信息，考虑到不同IMF在揭示故障特征时的有效性不同，本文采用基于Teager能量峭度(TEK)的加权平均方法获取WAEEMD滤波信号。综上所述，WAEEMD方法的具体流程如下：

(1)计算ci(t)的TEK值，其定义为[22]

(8)

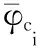
(2)计算加权平均系数w(i)，其定义为

(9)

(3)计算WAEEMD的输出结果z(t)，其表达式为

(10)

3 故障诊断方法的流程

基于WAEEMD和MSB的优势，本文提出WAEEMD-MSB方法用于滚动轴承的故障诊断。具体诊断步骤如下，其基本流程如图4所示。

图4 WAEEMD-MSB的流程

(1)使用EEMD将原始信号分解为一系列的IMF。

(2)使用式(8)计算每个IMF的TEK值。

(3)通过式(9)计算加权系数，并将其分配给相应的IMF，以获取WAEEMD滤波信号。

(4)应用MSB对WAEEMD滤波信号进行解调并提取故障特征频率。

4 仿真分析

为了验证所提出WAEEMD-MSB方法的有效性，针对滚动轴承外圈故障开展了仿真实验。滚动轴承外圈故障的仿真振动信号x(t)表示为

(11)

ti=t-(l/fo)

式中，Al(ti)为第l个脉冲的幅值；L为脉冲个数；u(ti)为单位阶跃函数；fo为故障特征频率，fo=88.5 Hz；α(ti)为阻尼系数；wr为共振频率；n(t)为带有信噪比为-7.14 dB的高斯白噪声。

图5示出了仿真信号的时域波形和频谱。从图5b中我们无法准确地提取故障特征频率。

(a)时域波形

为了更加准确地提取轴承外圈故障频率及其谐波，应用WAEEMD-MSB方法处理仿真信号。首先，将图5a中的仿真信号通过EEMD分解为18个IMF，其基于TEK的加权平均系数如图6所示。然后，将每个IMF与相应的加权平均系数进行乘积操作来获取WAEEMD滤波信号，其频谱如图7所示。此时仍然无法有效地提取故障特征频率fo及其谐波。最后，将MSB用于WAEEMD滤波信号，以分解调制分量并抑制背景噪声，从而提取故障特征频率，其分析结果如图8b所示，此时可以清楚地看到故障特征fo及其谐波。由此表明所提出WAEEMD-MSB方法能够有效地抑制噪声和分解干扰调制成分。

图6 基于TEK的加权平均系数

图7 WAEEMD滤波信号的频谱

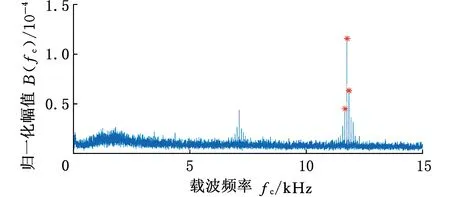
(a)MSB切片

5 实验验证

为验证所提出的WAEEMD-MSB方法的有效性，对感应电动机轴承外圈故障和平行轴齿轮箱轴承内圈故障的实验信号进行分析。滚动轴承试验台如图9所示，该试验台由直流发电机、感应电动机、平行轴齿轮箱、挠性联轴器和两个加速度传感器组成。在实验中，一个加速度传感器安装在感应电动机驱动端轴承座的垂直方向上，另一加速度传感器安装在平行轴齿轮箱壳体上。轴承的故障模式包括电动机轴承外圈故障和行星齿轮箱轴承内圈故障，如图10所示。表1和表2分别表示故障轴承的主要参数和故障特征频率。

图9 滚动轴承试验台

(a)外圈故障

表1 滚动轴承的主要参数

表2 滚动轴承的故障特征频率

5.1 平行轴齿轮箱轴承的分析结果

图11表示平行轴齿轮箱轴承内圈故障信号的时域波形和频谱。可以看出，被测信号非常复杂，而且有用的故障信息被背景噪声和干扰成分所掩没。从图11b很难识别故障特征频率fi及其谐波。为了更加准确地提取故障特征频率及其谐波，采用WAEEMD-MSB方法分析平行轴齿轮箱轴承内圈故障的振动信号。首先，将图11a中的振动信号通过EEMD分解为15个IMF，其计算的加权平均系数如图12所示。图13表示WAEEMD滤波信号的频谱。显然，由于强烈的背景噪声和干扰成分的存在，它无法有效地提取故障特征频率fi及其谐波。

(a)时域波形

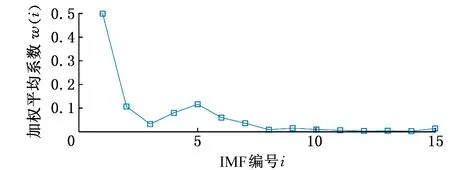
图12 基于TEK的加权平均系数(轴承内圈故障)

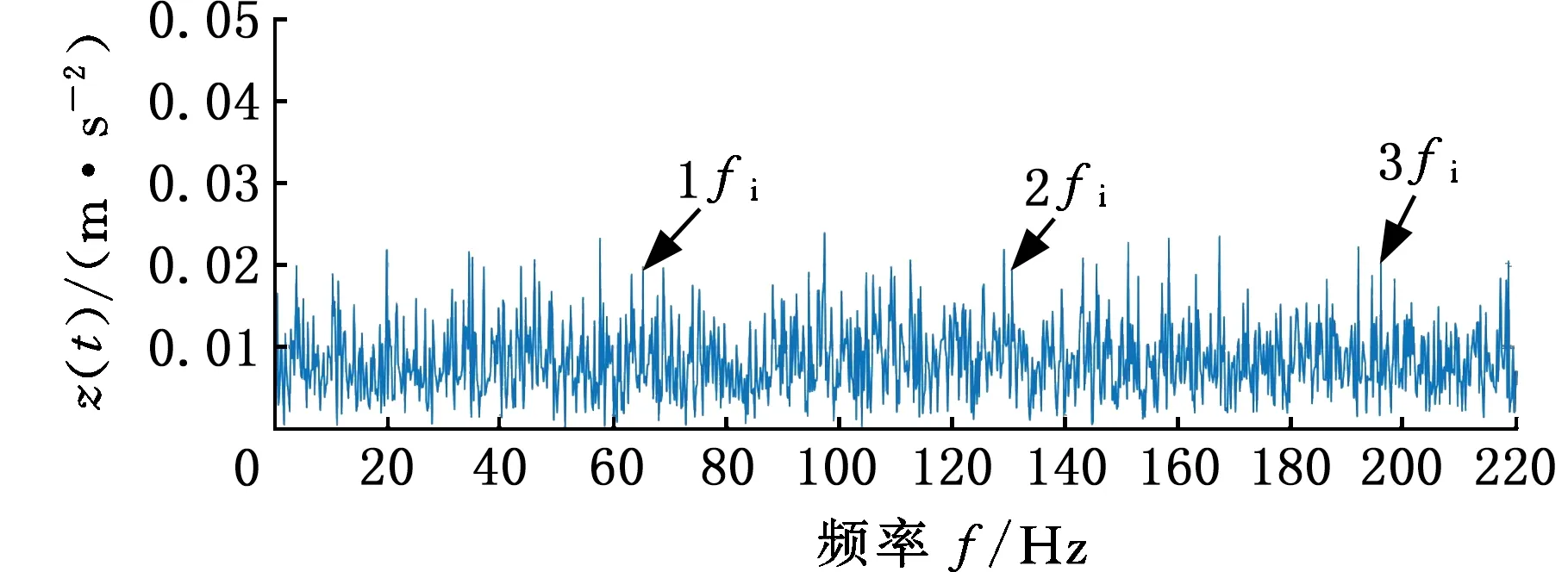
图13 WAEEMD滤波信号的频谱(轴承内圈故障)

然后，将MSB用于WAEEMD滤波信号，以分解调制分量并抑制背景噪声，从而提取故障特征频率，其分析结果如图14a所示。由图14a可以清楚地看到故障特征fi及其谐波。此外，应用快速谱峭度(FK)[23]和EEMD-MSB方法对平行轴齿轮箱轴承内圈故障信号进行分析，其分析结果分别如图14b和图14c所示。从图14b中可以看到故障特征频率fi及其谐波，但是FK的频谱混有大量的背景噪声，而且存在着一些干扰谐波。对于EEMD-MSB方法，选择IMF1(第1个IMF)作为最敏感的IMF，因为它具有最大的TEK值，这表明与其他IMF相比，IMF1含有最多的故障特征信息。图14c表明EEMD-MSB的频谱无法准确地获得故障特征频率。上述分析结果表明，相比FK和EEMD-MSB方法，WAEEMD-MSB方法能够更准确地提取轴承内圈故障特征信息。

(a)WAEEMD-MSB

为了进一步证明WAEEMD-MSB方法的有效性，采用特征频率强度系数(CFIC)来分别评估FK、EEMD-MSB和WAEEMD-MSB三种方法的性能，其定义如下[24]：

(12)

式中，Y(fj)为所选频带(0～220 Hz)中的幅值；Y(kf)为故障特征频率在第k次谐波处的幅值。

CFIC值越大，表明降噪方法的滤波效果越好。FK、EEMD-MSB和WAEEMD-MSB方法的CFIC值依次为0.73%、0.15%、7.66%。WAEEMD-MSB方法的CFIC值高于FK方法和EEMD-MSB方法，因此，进一步证明了WAEEMD-MSB方法比FK方法和EEMD-MSB方法更能有效地提取故障特征。

5.2 感应电动机轴承的分析结果

图15所示为感应电动机轴承外圈故障信号的时域波形和频谱。可以看出，被测信号具有很强的背景噪声和干扰成分，因此，很难识别电动机轴承外圈故障特征频率。

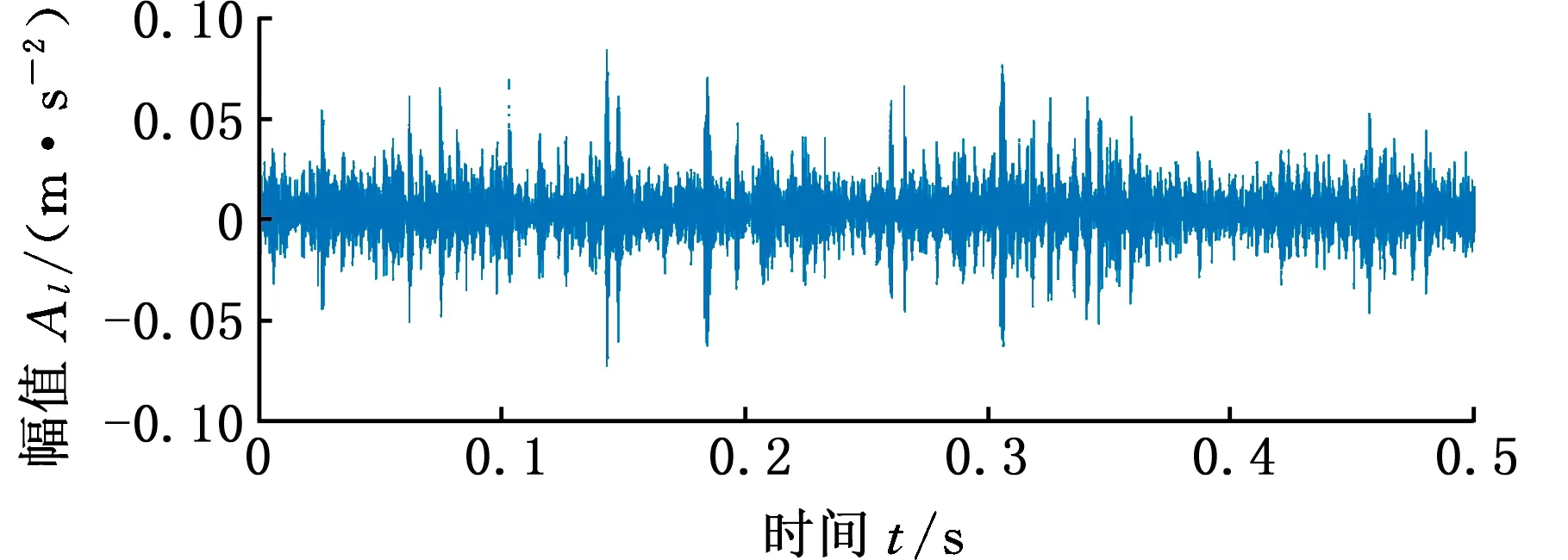
(a)时域波形

采用WAEEMD-MSB方法分析图15a所示的振动信号。首先，采用EEMD将感应电动机轴承外圈故障信号分解为15个IMF，其计算的加权平均系数如图16所示。WAEEMD的滤波信号的频谱如图17所示，无法有效地提取故障特征频率fo及其谐波。随后，将MSB应用于WAEEMD滤波信号，分析结果如图18a所示，可以清楚地看到故障特征fo及其谐波。此外，本文采用FK和EEMD-MSB两种方法对感应电机轴承外圈故障信号进行分析，其分析结果如图18b和图18c所示。基于FK分析的频谱可以反映故障特征频率，但是存在着大量的背景噪声和干扰频率(图18b)。尽管EEMD-MSB分析结果中也能够提取出故障特征频率及其谐波，但是在高次谐波处混有干扰频率成分(图18c)。为了进一步证明WAEEMD-MSB方法的有效性，仍然采用CFIC准则来评估上述三种方法。FK、EEMD-MSB和WAEEMD-MSB三种方法的CFIC值依次为4.26%、7.24%、26.62%。显然，WAEEMD-MSB方法优于FK方法和EEMD-MSB方法。因此，WAEEMD-MSB方法可以更准确、更有效地识别故障特征频率fo及其谐波。

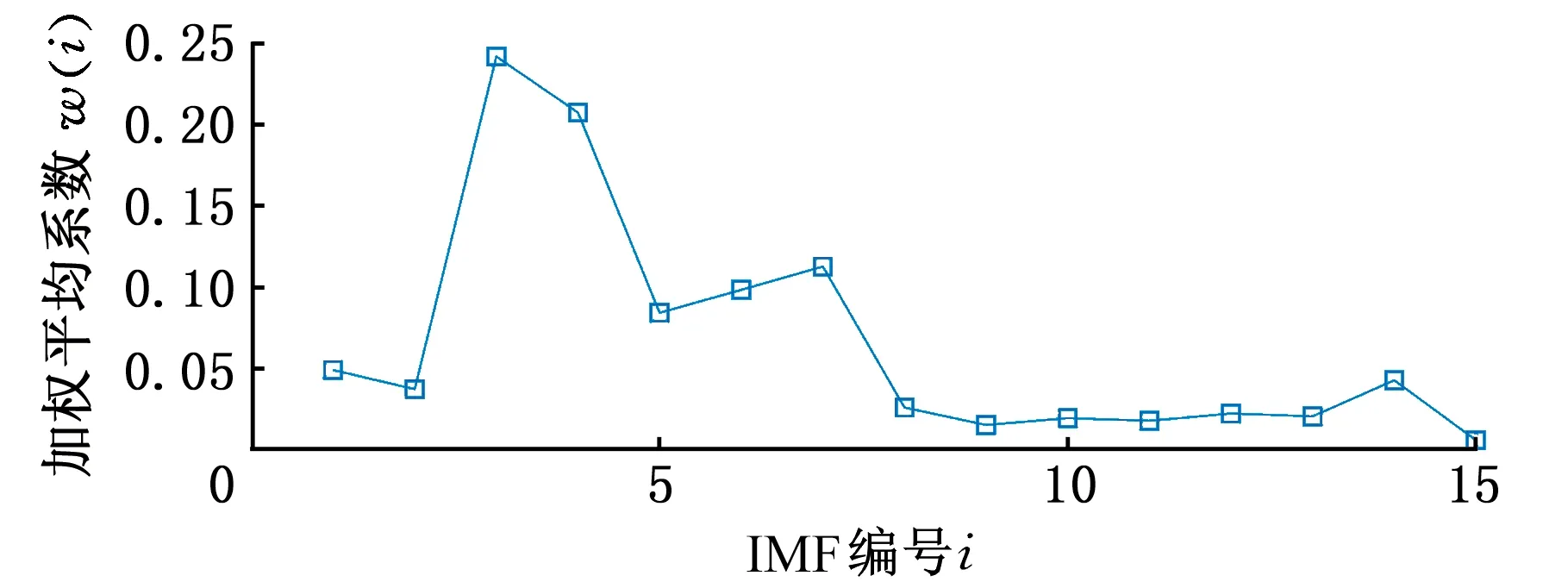
图16 基于TEK的加权平均系数(轴承外圈故障)

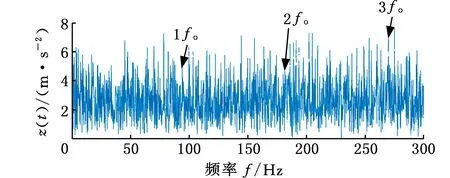
图17 WAEEMD滤波信号的频谱(轴承外圈故障)

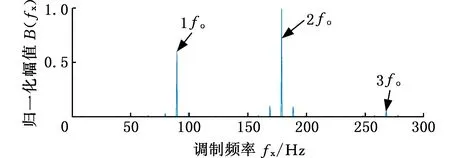
(a)WAEEMD-MSB

6 结论

本文提出了一种基于WAEEMD和MSB的滚动轴承故障特征提取方法。通过对平行轴齿轮箱轴承和感应电动机轴承故障诊断的研究，得出以下结论：

(1)基于TEK的加权平均系数能够突出显示敏感的IMF，同时减少来自其他IMF的干扰。

(2)WAEEMD可以有效解决MSB处理非平稳信号时的弱点，并进一步提高故障特征提取的精度。

(3)利用MSB对WAEEMD滤波信号进行解调以增强故障诊断的精度。

(4)通过对两种不同类型的滚动轴承故障的诊断，证明了WAEEMD-MSB方法的可行性和有效性。而且，WAEEMD-MSB方法比FK方法和EEMD-MSB方法更能够准确地提取轴承的故障特征。