基于响应面法的井下旋流分离器结构优化

邢 雷 李金煜 赵立新 蒋明虎 韩国鑫

1.东北石油大学机械科学与工程学院，大庆，1633182.黑龙江省石油石化多相介质处理及污染防治重点实验室，大庆，163318

0 引言

目前，我国油田含水率超过95%的油井多达四万余口，大量高含水油井的出现一方面使举升、集输和污水处理能量消耗及基建费用急剧增加，另一方面，污水处理化学试剂的大量使用使油田开发面临的环保压力越来越大[1]。如何降低油井举升及地面污水处理成本，实现油田中后期经济开采是保障国家能源战略的关键[2]。

同井注采技术可实现井下油水分离(即水相回注到地下水层，油相举升至地面)，可有效降低传统举升方式中的无效水循环及地面水处理负荷，减少地面注水管网建设，使高含水、特高含水油井实现经济开采，大幅提高采收率，为保障我国石油能源供给战略、实现稳油控水和节能降耗提供技术支撑。研发出适用于采用井筒内的油水分离设备以及进一步提高井下油水分离精度是保障同井注采工艺高效稳定运行的技术关键。

水力旋流分离器因具有设备小型、分离高效的特点已被应用于井下油水分离领域，为适应井下狭窄套管空间，赵立新等[3]、盛庆娇[4]、宋民航[5]相继提出了径向尺寸相对较小的可实现轴向进液的螺旋流道式及导流叶片式水力旋流器，并采用单因素法对两种旋流器进行了结构参数优选。王振波等[6]针对导叶式旋流器开展离散相运动行为分析，建立了粒级效率数学模型，研究得出最佳油水分离效率可达92.23%。赵传伟等[7-8]提出了一种切向进液式的井下两级式水力旋流器结构，并针对两级串联旋流器开展流场特性及分离性能评估，确定出了井下油层产量在120～140 m3/d范围内时，最佳分流比为0.36～0.74，为两级串联旋流器的进一步现场应用提供了指导和参考。王羕[9]、邢雷等[10]设计了一种井下轴入式两级串联旋流器结构，针对串联过渡区域开展结构参数优选研究，确定出了特定参数下最佳处理量为4.8 m3/h，最佳分流比为32%，并获得了处理量、分流比对流场特性及分离性能的影响规律。目前已经形成了多种形式的井下油水旋流分离器结构，相关学者采用数值模拟、流场测试及实验研究等方法对井下旋流器的流场特性、介质分布规律及分离性能等开展了大量研究，为拓宽旋流器应用范围，提高井下油水分离精度提供理论依据[11]。随着同井注采技术的进一步推广应用，所面临的井况愈加复杂化，井内出砂、含聚、含气及产液量的变化都会对井下旋流器的分离性能产生影响[12-14]，因此有必要开展旋流器的结构优化，以提高井下旋流器的适用性。部分学者采用单因素优选[15-16]、正交试验设计[17]等方法对水力旋流器的各项结构参数开展了大量研究，但上述方法无法构建各结构参数与优化目标间的数学关系，仅能在试验组所涉及的因素水平范围内进行参数优选。ZHAO等[18]采用响应面法对井下两级串联水力旋流器进行结构参数优化，构建了结构参数与底流管含油体积浓度间的数学关系模型，形成了水力旋流器的多参数优化方法，确定出了最佳结构参数配比，并通过实验对优化方法进行了验证，优化后结构的底流含油质量浓度较优化前结构的底流含油质量浓度降低了54.7%，该研究为井下旋流器的优化提供了思路。

目前关于井下轴入式水力旋流器的优化研究主要采用单因素法和正交试验法[19]，本研究在已有井下旋流分离器结构的基础上，基于响应曲面优化方法建立了可预测结构参数与分离效率及底流压力损失间的数学模型，并验证了模型预测及优化结果的准确性。

1 结构及工作原理

同井注采系统主要由采出泵、桥式通道、井下旋流分离器、封隔器、回注泵等配套装置构成，主要安装方式及流道布置如图1a所示。为了减少产出液在进入井下旋流分离器时的乳化现象，同时保障在采油井筒内实现分流比的实时调节，在井下分别设置采出泵及回注泵，形成双泵抽吸式井下油水分离及同井回注系统。系统工作时，井下产出液在地层压力作用下由入口进入到分离器内，经过螺旋流道后使液流的轴向运动逐渐转变为切向运动，在分离器的旋流腔内形成高速的切向旋转流场。在旋流场内离心力的作用下，密度较小的油相向轴心聚集，水相则运动至边壁。分离器轴心区域的富油相在采出泵的抽吸作用下，沿分离器的溢流口进入到溢流腔内，进而被举升至地面。分离后的净化水则在底部回注泵的抽吸作用下进入到底流腔内，进而经回注螺杆泵回注至地下水层，至此完成采油井筒内的油水分离器及同井回注。井下旋流分离器的主要结构形式如图1b所示，由溢流管、入口腔、螺旋流道、导流锥、大锥段、小锥段及底流管等部分组成，初始结构参数按照实验室前期通过单因素法优化后的数据确定[10]，主要结构参数尺寸见表1，其中Ls为螺旋流道长度，L1为导流锥长度，L2为大锥段长度，L3为小锥段长度，L4底流管长度L4，D为旋流分离器的主直径，du为溢流管直径。在构建流体域数值分析模型时，螺旋流道结构参数遵从文献[4]优化后结果，由于旋流分离器的径向尺寸受到井下空间的限制，因此在开展优化研究时需保障旋流器的径向尺寸不变，同时保持文献[20-21]确定的主直径、小锥段直径及底流管直径之间的最佳比例关系(图1b)不变，对分离器的导流锥长度L1、大锥段长度L2、小锥段长度L3、底流管长度L4以及溢流管直径du的参数尺寸进行优化分析。以上述5个结构参数为输入自变量，以旋流器分离效率以及压力损失为因变量，分别构建结构参数与分离效率及底流压力损失间的数学关系模型，进而确定出最佳的多参数优化匹配方案。

(a)同井注采系统工艺简图

表1 井下旋流分离器主要结构参数

2 研究方法

2.1 响应面法基本原理

响应面优化方法可以将复杂的未知函数关系在一定区域内用简单的一次或二次多项式模型拟合，在试验条件范围内寻优时，可对不同因素的不同水平实现连续分析，进而获得较为准确的最优解[22]。由于二阶多项式模型具有较高的精度且模型简单，可预测性强，因此本文选用二阶多项式模型，分别构建输入指标(导流锥长度L1、大锥段长度L2、小锥段长度L3、底流管长度L4以及溢流管直径du)与响应目标(分离效率及压力损失)间的函数关系。选用的二阶多项式模型基函数为[23]

(1)

其中，y为响应目标，本文中分别代表井下旋流分离器的分离效率及压力损失；xi、xj为独立设计变量，本文中代表被优化的结构参数；k为设计变量的数量，本文针对5个不同结构参数开展优化研究，所以k=5；β0为回归方程常数(即偏移项)；βi、βii、βij分别为回归方程的线性偏移系数、二阶偏移系数和交互系数。

2.2 数值模拟方法

2.2.1数学模型

数值模拟过程中水和油两相的连续性方程分别如下[24]：

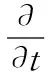
(2)

(3)

式中，φc、ρc、uc分别为连续相(水)的体积分数、密度和速度矢量；φd、ρd、ud分别为分散相(油)的体积分数、密度和速度矢量。

采用欧拉-欧拉的方法模拟水-油两相流，在此方法中，每一相都有单独的质量和动量守恒方程，对于不可压缩流体来说，以水相为例，其平均动量方程可表示为

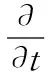
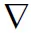
(4)

考虑油滴直径以及油水两相间的密度差相对较小，因此忽略升力和虚拟质量力对油滴的影响，只考虑曳力和湍流耗散力。其中曳力的计算表达式如下[25]：

(5)

其中，dd为离散油滴的直径；CD为曳力系数，根据Schiller-Naumann经验公式，CD可通过如下公式计算：

(6)

式中，Red为油滴的雷诺数。

湍流耗散力可表示为

(7)

式中，CTD为湍流耗散系数；υt，c为水相湍流运动黏度；Scd为油相湍流施密特数。

采用精确度较高的雷诺应力模型完成流场中湍流的计算。雷诺应力输运方程可表示为[26]

(8)

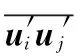
2.2.2参数设置及边界条件

油水两相间模拟计算采用多相流混合模型(Mixture模型)。以含水率为98%、产液量为96 m3/d的油井为研究对象，设置井下油水分离器入口为速度入口，入口流量为4.0 m3/h，依据产出泵与注入泵的抽吸比，设置溢流及底流的分流比为1∶4。同时依据现场原油物性参数，数值模拟时设置油相密度为850 kg/m3，油相动力黏度为1.03 Pa·s，水相动力黏度为1.003 mPa·s，油相体积分数为2%。选用双精度压力基准算法隐式求解器稳态求解，湍流计算选用Reynolds应力方程模型，SIMPLEC算法用于进行速度压力耦合，墙壁设置为无滑移边界条件，动量、湍动能和湍流耗散率设为二阶迎风离散格式，收敛精度设为10-6，壁面设置为不可渗漏、无滑移边界条件。

3 结果分析

3.1 CCD试验设计及方程构建

响应面分析的试验设计方法有中心组合设计(central composite design，CCD)和Box-Behnken设计(BBD)、二次饱和设计、均匀设计、田口设计等，其中较为常用的试验设计方法主要为CCD及BBD两种。CCD试验设计的空间点分布如图2所示，其中1表示设计因素的上水平，-1表示设计因素的下水平。CCD试验设计有利于更好地拟合出各个因素与输出指标间的响应关系，由于轴向点α值的存在，致使CCD获得最优解过程的搜索范围较BBD获得的搜索范围更广[27]，因此本文采用CCD试验设计方法确定结构参数对井下油水旋流分离器分离效率及压力损失影响的试验方案。将本研究团队前期采用单因素法获得的最佳实验结果作为本次正交试验的中心点，设计各因素水平及编码值如表2所示。

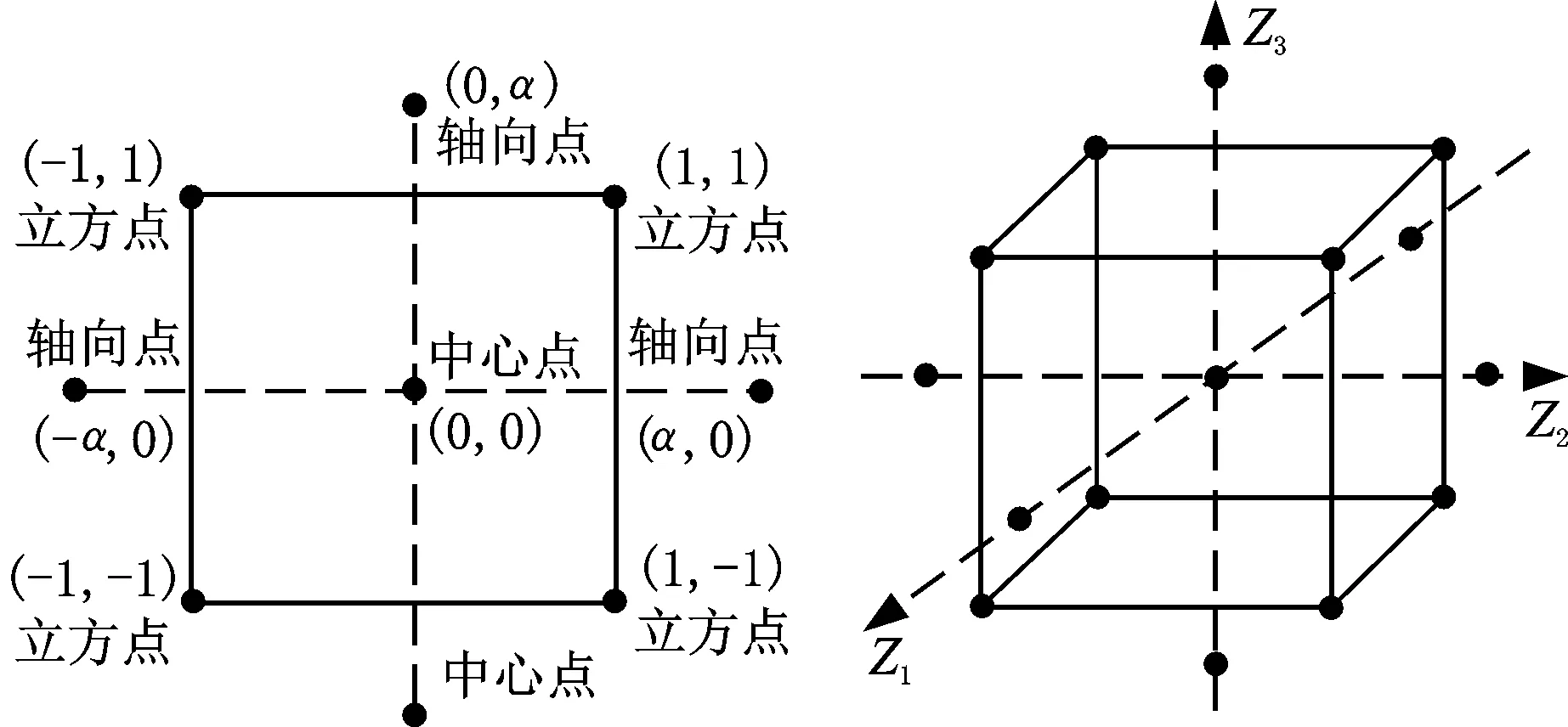
(a)设计点二维投影分布图 (b)设计点三维分布图

表2 CCD试验因素水平设计

基于CCD试验设计方法，以待优化的5个结构参数为自变量，设置因素数为5，中心点试验重复次数为8，轴向点α值为2.3784。因变量个数为2，分别为井下油水旋流分离器的分离效率Ez与底流压降值(压力损失)Δp。其中底流压力损失计算方法为入口截面上的平均静压值减去底流出口截面上的平均静压值[28]。分离效率的计算表达式如下：

(9)

式中，f为溢流分流比；Cd为底流出口油相质量浓度，mg/L；Ci为分离器入口油相质量浓度，mg/L。

基于表2中不同结构参数因素水平，形成CCD试验设计50组，按照不同试验设计组的结构参数分别完成井下旋流分离器的流体域模型建立，对模型进行相同水平的网格划分并开展数值模拟分析，再对不同试验组的分离效率Ez及底流压力损失Δp进行计算，最终得出响应面试验设计方案及数值模拟结果如表3所示。

采用二阶模型对表3所示的结果数据进行二次多项式拟合，通过多元线性回归分析可得出优化结构参数与井下旋流分离器的分离效率y1和底流压力损失y2之间的回归方程分别如下：

表3 CCD设计及试验结果

(10)

y2=451.062 48-3.102 71x1-2.331 14x2+0.014 554x3-0.032 99x4-3.047 23x5+0.015 048x1x2-

1.736 56×10-4x1x3-5.903 13×10-5x1x4+5.540 63×10-3x1x5-6.685 94×10-5x2x3+1.404 53×

10-4x2x4-4.782 81×10-3x2x5-6.822 19×10-5x3x4+1.295 94×10-3x3x5-1.135 31×10-3x4x5+

(11)

3.2 方差分析

采用方差分析法对响应面构建的5个结构参数与分离效率及压力损失间的数学模型分别进行显著性检验，可得出表4所示的方差分析结果。由表4可知，结构参数与分离效率y1及压力损失y2间的回归方程的P<0.0001<0.05，表明两个回归方程所反映的函数关系均显著，说明在表2所示的上下限参数变化范围内，可以用两个回归方程(式(10)和式(11))分别对井下旋流器的导流锥长度L1、大锥段长度L2、小锥段长度L3、底流管长度L4以及溢流管直径du多参数条件变量下的分离效率及底流压力损失值进行预测。

表4 回归方程的方差分析结果

为了验证回归方程的预测精度，对式(10)和式(11)分别进行误差统计分析，可得出表5所示的误差统计分析结果。由表5可知，相关系数R-Squared值越接近1，说明相关性越好；Adj R-Squared及Pred R-Squared值越大且越相近，说明回归模型可更加充分地反映输入与输出变量间的关系；变异系数小于10%，说明试验结果具有较高的精度及可信度；Adeq Precision为有效信号与噪声的比值，该值大于4说明模型合理。统计分析结果表明，所得的回归模型均符合上述检验原则，说明两个模型均具有较好的适用性。

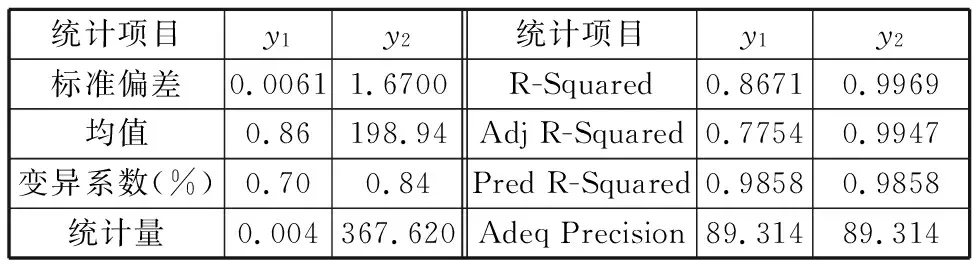
表5 回归模型误差统计分析结果

3.3 模型求解及精度验证

为了验证导流锥长度L1、大锥段长度L2、小锥段长度L3、底流管长度L4以及溢流管直径du五个结构参数在表2所示范围内变化时，反映结构参数与分离效率间的预测模型(式(10))以及反映结构参数与底流压力损失间的预测模型(式(11))的预测结果准确性，在各因素上限及下限范围内随机取值，开展10组不同于表3试验中参数匹配的随机附加试验，附加试验的结构参数取值如表6所示。

表6 附加试验组结构参数

按照表6所示附加试验的结构参数分别构建井下油水分离器流体域模型，采用与响应面试验相同的数值模拟方法对附加试验组开展数值模拟分析。通过将10组附加试验参数代入式(10)、式(11)可得出不同附加试验组的模型预测值与数值模拟实际值的对比情况，如图3所示。由图3可以看出，无论是分离效率还是压力损失，预测值及实际值随不同附加试验组均呈现出了相同的规律性，说明预测值与实际值呈现出了较好的一致性。为了对预测值的精度进行核验，采用下式对预测值与实际值的平均相对误差进行计算：

图3 模型预测值与数值模拟实际值对比

(12)

式中，ei为第i组附加试验的模型预测值；ti为第i组附加试验模拟得到的实际值；n为附加试验组数。

通过计算得出不同附加试验组分离效率的模型预测值与实际值的平均相对误差Δ1=0.104%，压力损失的模型预测值与实际值的平均相对误差为Δ2=4.562%。可以看出模型预测值与实际值间的平均相对误差很小，从而验证了模型预测结果的准确性。

3.4 优化结果及验证

采用最小二乘法对构建的结构参数与分离效率间的回归方程进行偏微分求导，计算得出可使分离效率取极大值的结构参数匹配方案即为响应面优化后的最佳设计点。计算得出优化后结构参数分别为导流锥长度L1=20.3 mm、大锥段长度L2=60.6 mm、小锥段长度L3=635.7 mm、底流管长度L4=489.2 mm、溢流管直径du=10 mm，优化前后井下旋流分离器的结构参数变化如图4所示。图5所示为大锥段及小锥段上，不同截面过轴心截线的油相体积分数分布曲线的对比。由图5可以看出，在截面Ⅰ及截面Ⅱ上，与优化前结构相比，优化后旋流分离器在轴心区域的油相体积分数明显更大，说明优化后的结构可使更多的油相聚集在临近油相出口的轴心区域，从而使更多的油相由溢流口流出，提高旋流器的油水分离性能。数值模拟结果表明，优化后结构的油水分离效率可达88.35%，明显高于优化前结构的油水分离效率86.01%。

图4 井下旋流分离器优化前后结构变化

图5 优化前后旋流器在分析截面上的油相体积分数对比

为了进一步验证优化后井下旋流分离器的高效性，针对优化前后井下旋流分离器的结构开展不同入口油滴粒径的数值模拟对比研究，入口油滴粒径分别设置为50 μm、100 μm、300 μm、400 μm、500 μm，数值模拟方法及边界条件与前述一致，对比在不同入口油滴粒径条件下优化前后旋流器的分离性能。数值模拟得出优化前后旋流器的分离效率对比情况如图6所示。由图6可以看出，随入口油滴粒径的增大，旋流器的分离效率均呈逐渐升高趋势。入口油滴粒径在50～500 μm范围内变化时，优化前结构的分离效率由58.92%提高到98.56%，优化后结构的分离效率由60.35%提高到99.48%，优化后结构的分离效率明显高于优化前结构的分离效率。这说明采用响应面优化后的旋流器结构对不同粒径油滴呈现出了更好的分离性能。

图6 不同油滴粒径条件下旋流器优化前后分离效率对比

为了验证不同含水率条件下优化后结构的适用性，开展了不同含水率条件下优化前后井下旋流分离器数值模拟对比研究。数值模拟时分别设置含水率为94%、95%、96%、97%、98%、99%，油滴粒径设置为300 μm，得出不同含水率条件下井下旋流器优化前后分离效率对比情况，如图7所示。图7结果显示，随着含水率的增加，旋流器的分离效率也逐渐提高。优化前结构的分离效率由74.61%提高到88.07%，优化后结构的分离效率由75.26%提高到91.56%。在不同含水率条件下优化后结构的分离效率均高于优化前结构的分离效率，优化后结构对不同含水率条件呈现出了较好的适用性。这充分验证了响应面优化结果的准确性及高效性。

图7 不同含水率条件下旋流器优化前后分离效率对比

4 结论

(1)采用响应面的中心组合设计(CCD)试验设计方法构建结构参数与分离效率及底流压力损失间的数学模型具有可行性。基于二阶多项式构建的分离效率预测模型的相关系数为0.8671，构建的底流压力损失预测模型的相关系数为0.9969。方差分析结果验证了模型具有较好的显著性及较高的精度。

(2)通过开展10组附加试验，验证了构建的数学模型可以对参数上下限范围内的分离效率及压力损失进行准确预测，分离效率的模型预测值与实际值的平均相对误差为0.104%，压力损失的模型预测值与实际值的平均相对误差为4.562%。

(3)基于构建的分离效率预测模型得出的优化结构参数可以有效提高井下旋流器的分离效率，针对油滴粒径在50～500μm范围内变化的采出液，优化后结构的分离效率最高可达99.48%，高于优化前结构的分离效率98.56%。针对含水率在94%～99%范围内变化的采出液，优化后结构的分离效率最高可达91.56%，高于优化前结构的分离效率88.07%。