直线共轭内啮合齿轮泵输出流量脉动的测试研究

陈宗斌 何 琳 廖 健

1.海军工程大学振动与噪声研究所，武汉，4300332.船舶振动噪声国家重点实验室，武汉，430033

0 引言

内啮合齿轮泵由于结构紧凑、简单可靠、流量脉动小等诸多优点，被广泛应用于注塑机、汽车传动、高端机床等领域。通常所指的内啮合齿轮泵为楔块式内啮合齿轮泵，又分为渐开线内啮合齿轮泵和直线共轭内啮合齿轮泵两类。由于齿形独特，直线共轭内啮合齿轮泵具有两大优势：一是困油容积小，且困油容积呈现逐渐增大的趋势，更有利于齿轮副的稳定传动；二是采用径向间隙固定式设计，无补偿措施，运行更加平稳，输出流量脉动更低，业界通常称其为安静性泵。

该泵最早由TRUNINGER[1]申请发明专利，但至今国外几乎没有相关研究文献和资料公开。SAUER、Bucher以及日本住友等公司购买了该专利并开发了成熟产品。国内关于直线共轭内啮合齿轮泵的研究最早始于1987年，煤炭科学研究总院上海分院周祥[2]研究了该型泵的运动学和动力学特性，此后董信根[3]分析了该泵的基本结构形式并研究了加工齿刀的线型，陈忠强等[4]通过解析式法推导了该泵的流量脉动特性。1992年，煤炭科学研究总院上海分院与上海航空发动机制造有限公司以国外第四代产品QT系列为研仿对象，开发了国内首款直线共轭内啮合齿轮泵——NB系列[5]。2004年，上海航空发动机制造有限公司又在上海理工大学的技术支持下，以国外第五代QX系列为研仿对象，形成了国内NBX系列直线共轭内啮合齿轮泵[6]，最高压力21MPa，容积效率87%。目前国产直线共轭内啮合齿轮泵的最高压力达32MPa，容积效率85%，振动噪声70 dB(A)左右，生产厂家主要有上海航空发动机制造有限公司、宁波布赫懋鑫液压技术有限公司、上海朋泰机械科技有限公司以及秦川机床集团有限公司等四家，相关企业的研发和设计能力不足，始终停留在试错与研仿阶段。近年来，SONG等[7]采用Litvin的数值建模方法，推导了直线共轭齿轮副设计方法，研究了该泵的流量脉动特性；魏伟锋等[8]采用参数化手段为直线共轭齿廓的设计提供了新方法；杨国来等[9]推导了齿形设计解析方法，采用Fluent流体仿真软件开展了初步仿真研究工作。低流量脉动是该泵的关键特性，但国内研究仍然集中在直线共轭内啮合齿轮副的齿形设计上，研究零散，系统性不强，很少有专门针对流量脉动的研究。

此外，由于泵源出口流量大，变化频率快，尚未有高频流量计可直接测定流量脉动，因此几乎没有专门针对该泵输出流量脉动特性的测试研究，少量研究也集中在流量推导和定性分析方面。为准确测量柱塞泵出口流量脉动，JOHNSTON[10]提出了伸缩管道测量法，通过测试不同长度管道下的压力信号计算出泵源阻抗和流量脉动，该方法测试流程繁琐，可操作性不高。余经洪等[11]提出了实用近似法，假设泵源流量与阻抗串联，分别测量油液综合体积弹性模量、终端阻抗、终端反射系数以及管路中某点处压力信号，进而根据管路波动方程计算出被试泵的流量脉动，该方法测试过程相对简单，但精确度不高。JOHNSTON等[12]提出了引入陪试泵的二次源测试方法，该测试方法准确方便，已被ISO推荐为标准测试方法[13]，该方法的难点在于测试数据处理复杂，影响测试精度的因素较多。近年来，徐兵等[14]也开展了二次源法的测试研究，但他们对具体的数据处理方法以及测试精度的影响因素并未开展深入研究，且研究对象主要集中于柱塞泵。

直线共轭内啮合齿轮泵流量脉动小，信噪比小，对测试的精度要求高，测试步骤和数据处理难度大。为准确了解该泵的输出流量脉动特性，本文针对该泵的流量脉动专门开展精确测试研究。在给出“二次源法”测试原理的基础上，重点研究了后期测试数据的处理方法，并详细分析了测试参数对测试精度的影响，给出了提高测试精度的建议，搭建测试平台并得到了直线共轭内啮合齿轮泵的实际流量脉动输出曲线。

1 测试原理

假设被测泵为泵源流量QS和泵源阻抗ZS并联的模型，如图1所示，图中，Po和Qo分别为泵源出口处的压力和流量，ZT为负载阻抗。基于波的传递理论和管道动态特性，可得

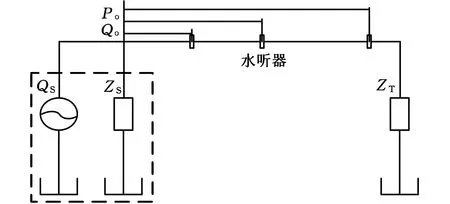
图1 被测泵简化模型

(1)

根据式(1)，为获取被测泵流量曲线，须先测得泵源阻抗ZS，为此，在管路终端引入陪试泵作为二次激振源。开启二次源陪试泵，视被测泵为负载终端，如图2所示，此时被测泵泵源出口处的流量和压力分别为QSo和PSo，则被测泵源阻抗

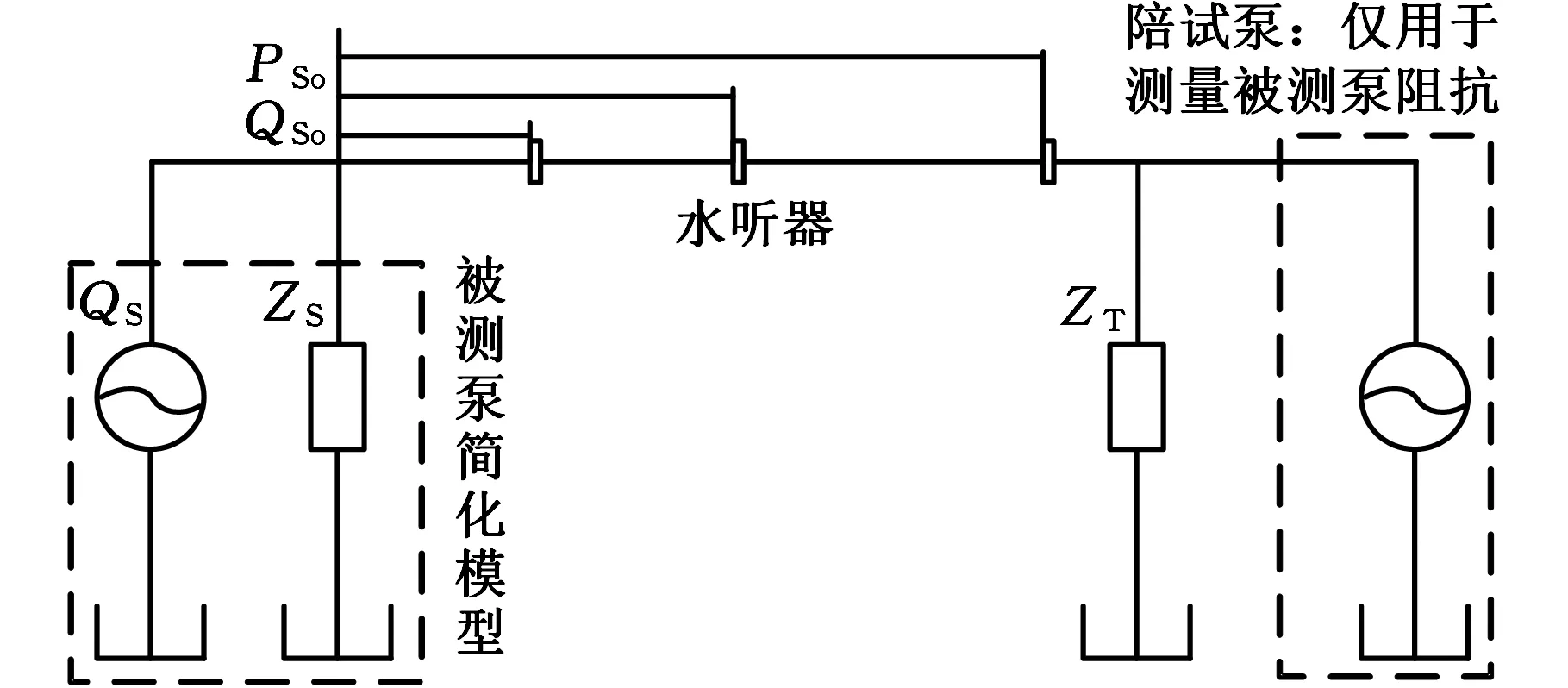
图2 二次源激振原理

(2)

根据管路波动方程，任一时刻管路中任一位置x处的压力流量有以下关系：

(3)

式中，ω为声波频率；γ为管路中声波传播常数；Z0为管路特征阻抗；F、G为边界条件系数。

流量测试难度大，压力容易测定。根据式(3)测定管路中两个不同位置x1和x2处的压力P1、P2，求解管路边界条件系数，即可得管路中的流量Q1和Q2。仅测试两个位置点的压力极易引入测试误差，同时若两点正好位于谐波波长整数倍处，则测试压力相等，数据无效，因此测试时至少选取三个测试点，显然测试点越多数据拟合精度越高。综合上述分析，二次源法测试泵源流量脉动可分为以下三步[12]：

(1)测试被测泵泵源阻抗。同时开启被测泵和陪试泵，应用式(3)得到被测泵泵源出口处QSo和PSo，应用式(2)求解源阻抗ZS。

(2)拟合全频带上的ZS值。步骤(1)中得到陪试泵谐频点处被测泵的阻抗值，采用线性插值法、分布参数法、集中参数法等不同拟合方法求解全频带上的泵源阻抗曲线。

(3)测试流量脉动。关闭陪试泵，开启被测泵，记录相同出口压力和流量工况下三个测点的压力脉动信号，应用式(3)得到被测泵泵源出口处的Po和Qo，应用式(1)求解泵源实际出口流量脉动。

2 测试精度影响因素分析

2.1 管路模型影响

根据不同假设条件，流体传输管道一般有三种模型：无损模型、线性摩擦模型以及耗散模型。为贴近实际情况，充分考虑黏性和热传递效应，实际测试中一般选用耗散模型。耗散模型引入了贝塞尔函数，增加了数据处理复杂程度，高频段计算结果存在不稳定性。为寻求合适的近似计算方法，常见的较精确近似方法有Foster等价剪切系数模型、高频近似模型以及一阶平方根近似模型等[15]，三种近似模型区别在于对管路修正系数处理不同。管路修正系数为

其中，λ为管路的等价剪切系数；J0和J1分别为第一类零阶和一阶贝塞尔函数。令

Foster等价剪切系数模型[16]、高频近似模型以及一阶平方根近似模型对应的贝塞尔函数B(λ)的简化函数如下：

三种不同模型下B(λ)的频率响应与贝塞尔函数精确解的对比曲线见图3和图4。低于10 Hz的低频段，三种模型的误差均较大；高频段，三组近似处理后的曲线与原响应曲线重合度较高；等价剪切模型在8 Hz左右有相位上的跳跃，高频近似模型在高频段重合度最高。直线共轭内啮合齿轮泵最小稳定运行转速下，流量脉动基频已大于100 Hz，因此低频段的估值误差可忽略不计。结合上述分析可知：管路的高频近似模型无论是在数据处理难度还是估值准确性上均优于其他模型，数据处理过程中建议选用管路的高频近似模型。

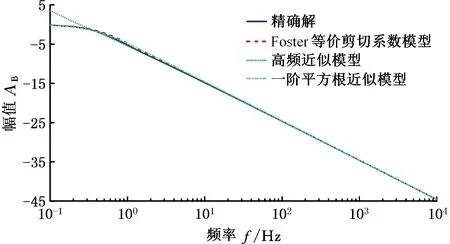
图3 B(λ)的幅值响应图

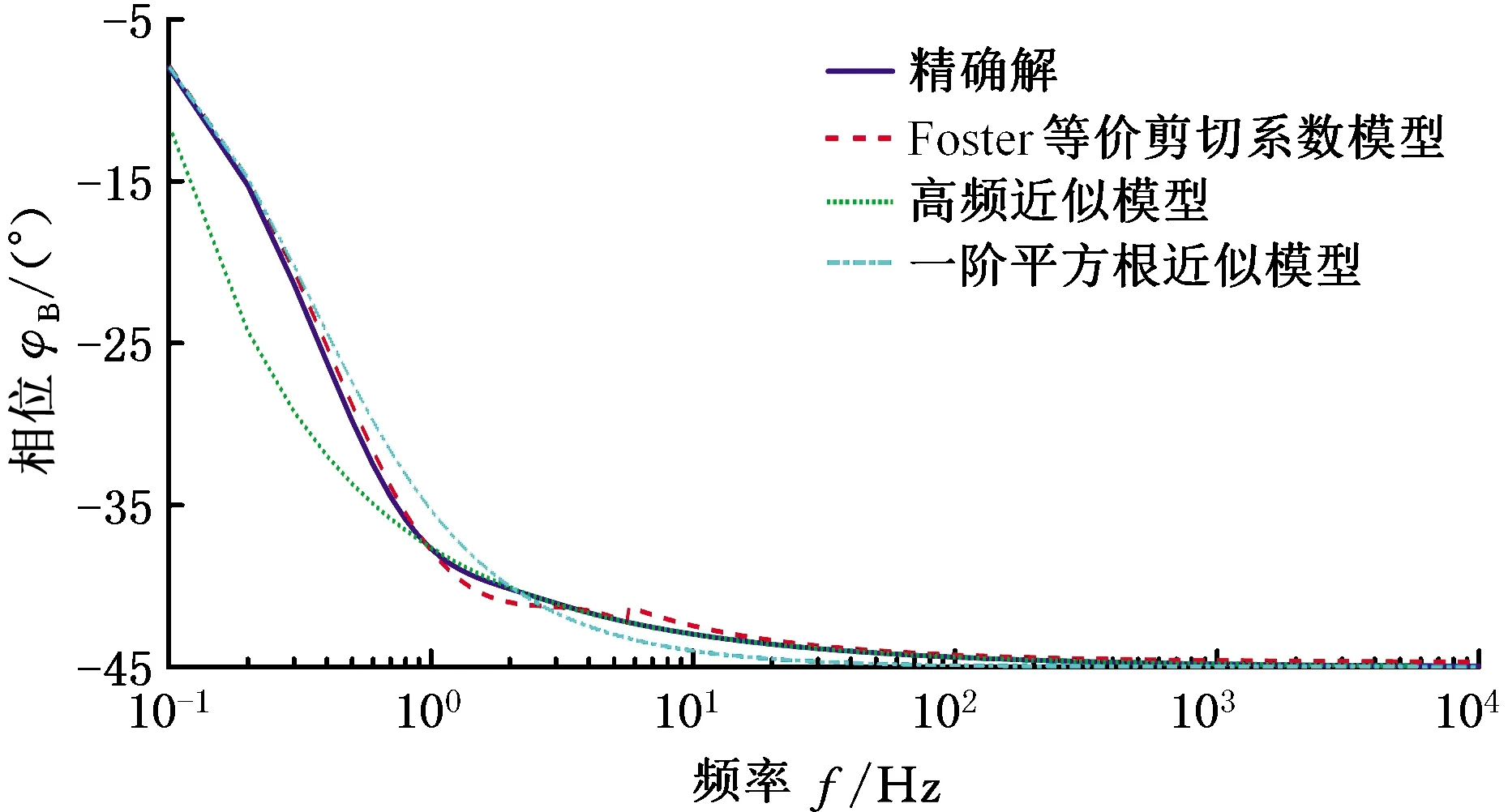
图4 B(λ)的相位响应图

2.2 体积弹性模量影响

在管路波动方程推导时，假设管壁为刚性。实际上大多数管壁均为弹性体，管内流体压缩时，管壁要同时发生膨胀，因此需要对弹性模量予以修正[13]：

式中，B、Beff分别为油液弹性模量和有效弹性模量；E为管材的弹性模量；d、e分别为管路的直径和壁厚；C1为测试管段支承情况的修正系数，弹性支承时C1=1。

为减小管路影响，实际测试时尽量选取壁厚较大、长直的硬质管，同时采用全周向包围弹性支承，减少管路的振动。测试过程中，液体中混入的气体也会影响油液的体积弹性模量[17]，即有

其中，x0为参考压力p0时的空气体积含量；xp为实际压力p时的空气体积含量；Boil、κ分别为油液的理论弹性模量和气体多变指数。油液中空气含量越高，体积弹性模量越小。为减小空气含量的影响，测试时应先启动泵源充分运行，稳定油温，以析出流体中的气泡，同时，要保证泵源吸油口吸油顺畅，防止吸空导致测试管路中产生气泡。

2.3 压力传感器安装形式影响

长度方向上，压力传感器距离泵源出口的位置应该互质，即压力测量位置应处于声波不同相位处，即

式中，Δx为传感器距离；c0为声速。

高度方向上，应避免图5所示的两种错误安装形式。如图5a的安装形式，插入的传感器易在管路中形成局部紊流，影响测试管路中层流流态的假设模型；如图5b的安装形式，传感器实际测试点距离管路中流体压力点仍有狭长流道，若流道内径为dt，长度为lt，传感器测试点压力pt，管路实际压力pa，则有[11]

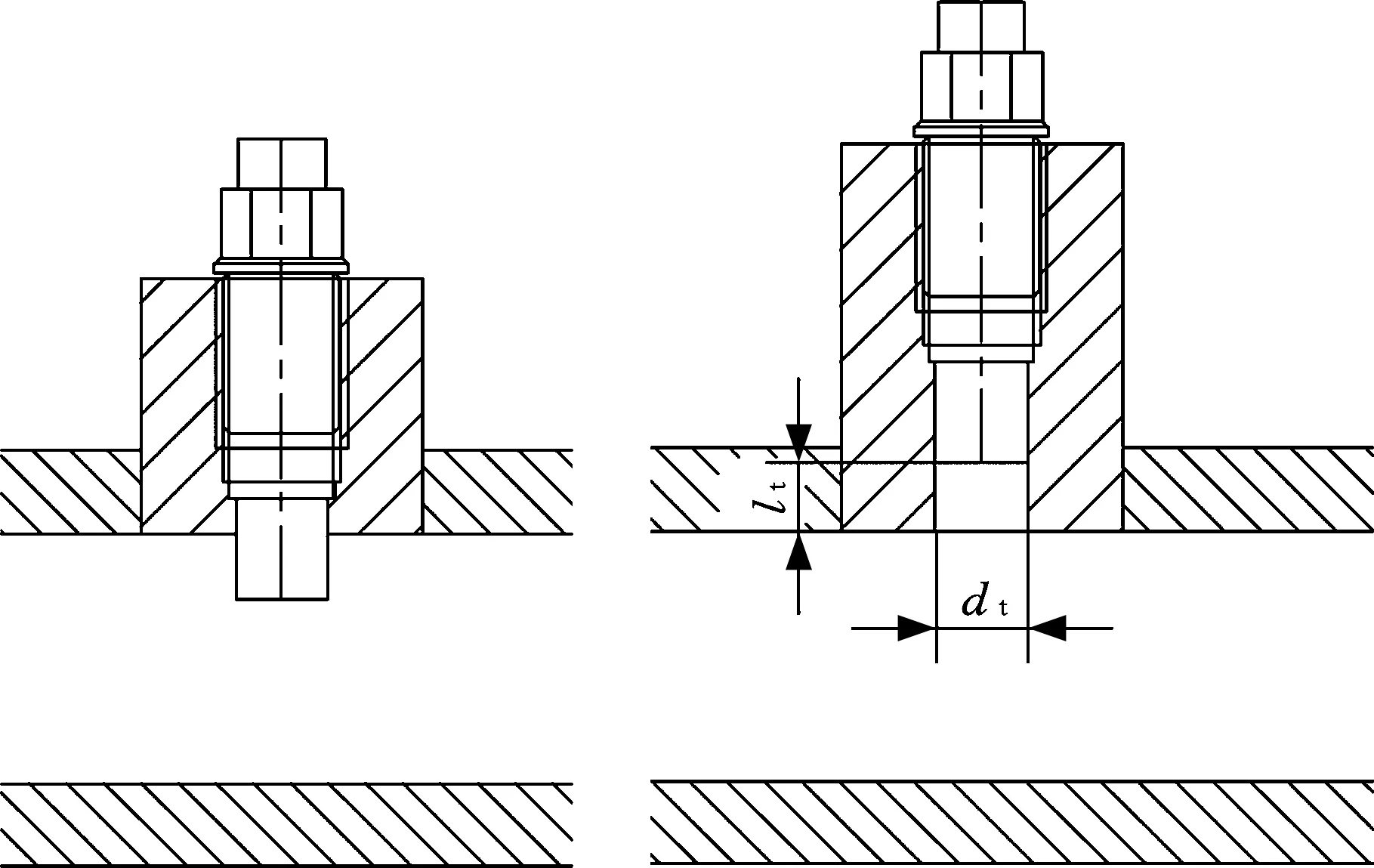
(a)传感器插入管内 (b)传感器端面远离管内壁

不同的流道孔径下，测试压力影响如图6和图7所示，传感器油道变化对测试结果的影响主要体现在1 kHz以上，实际测试时，测试频率至少达到3 kHz。为提高1 kHz以上高频段测试精度，建议尽量选择传感器油路为大孔短流道，保证传感器贴近测试管内壁。

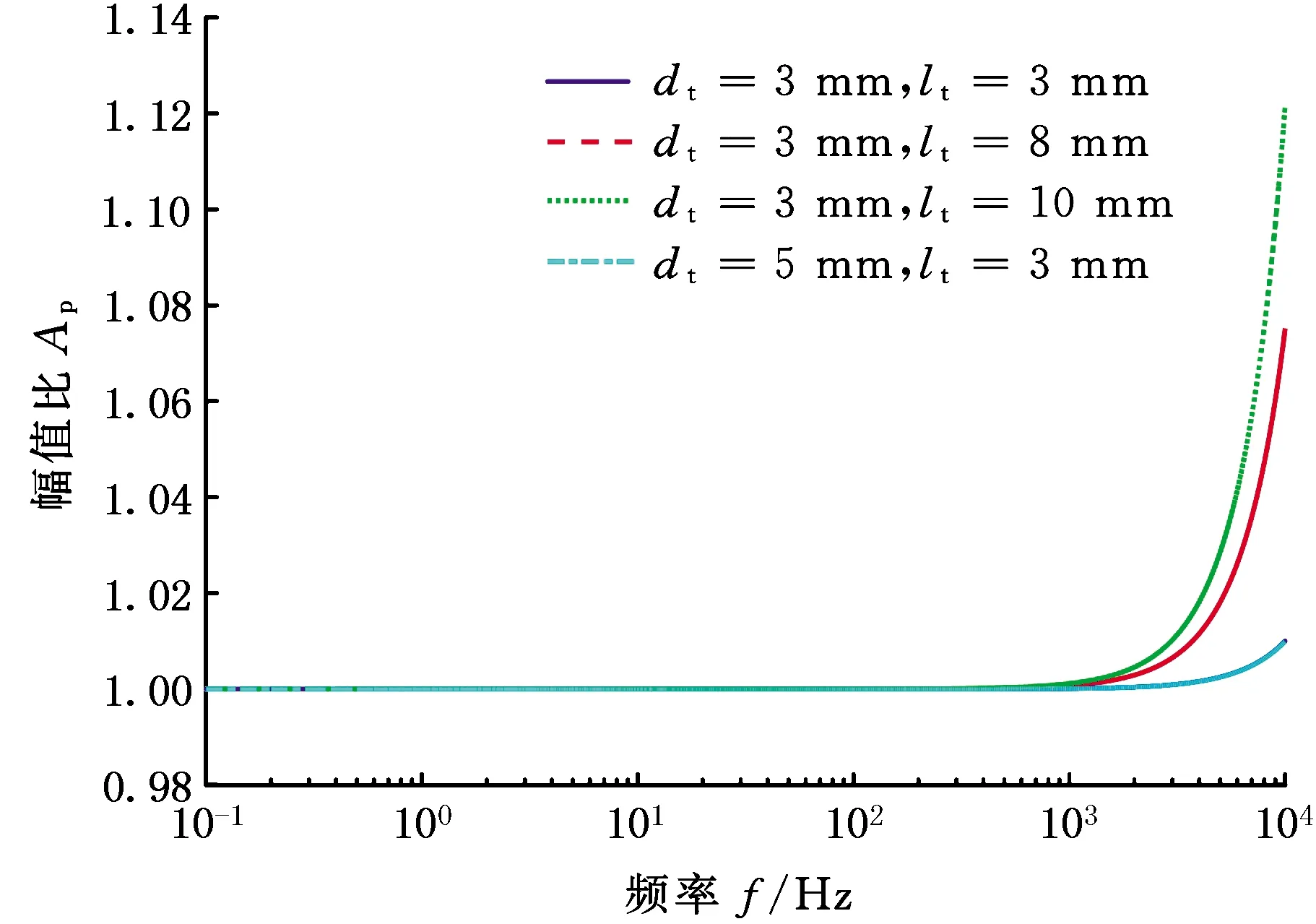
图6 pt/pa的幅值响应图

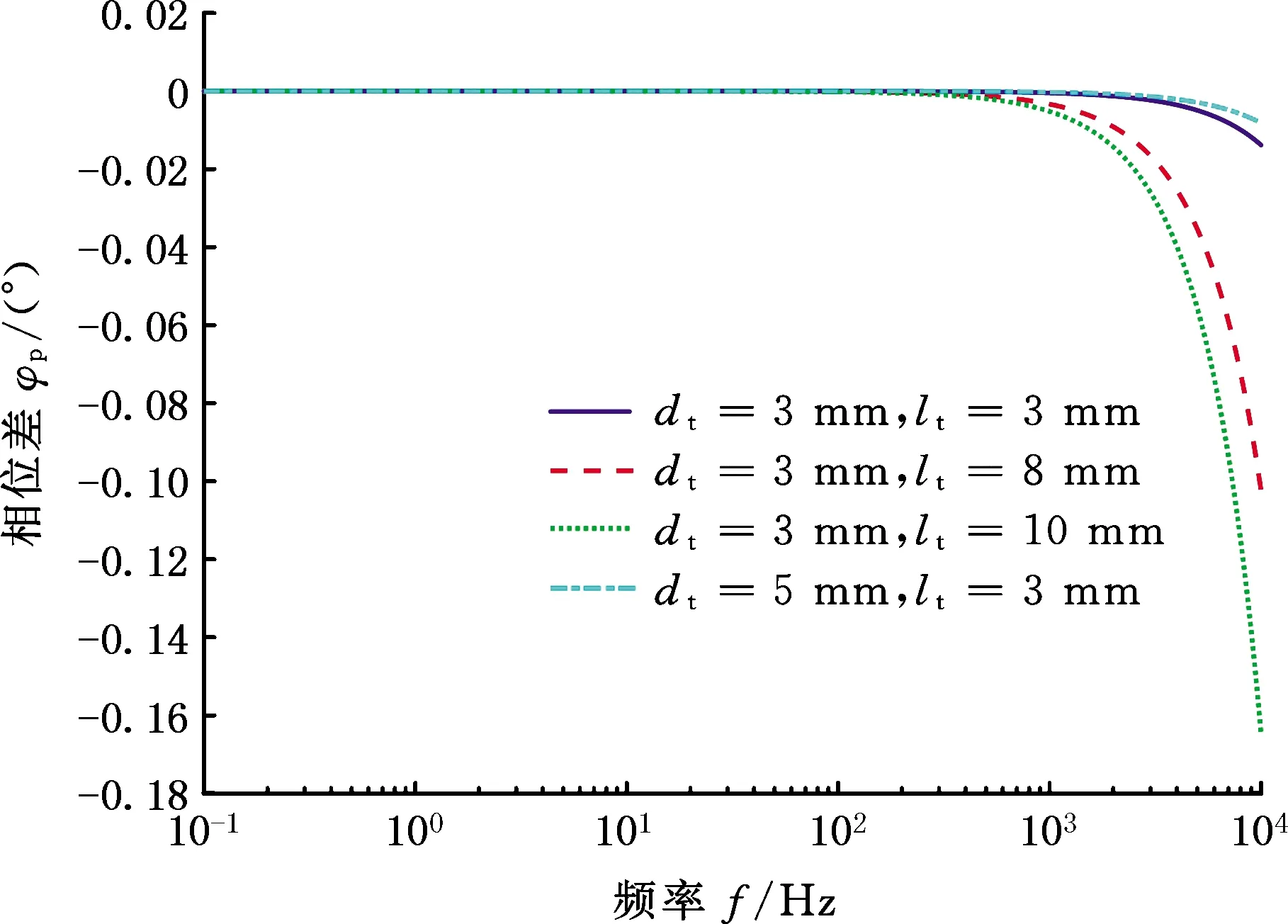
图7 pt/pa的相位响应图

2.4 全频带泵源阻抗拟合

泵源阻抗拟合是数据处理的难点，参与拟合的数据点越多，测试误差对结果的影响会减小，但在已获取测试数据点的情况下，拟合模型的选用以及有效数据点的取舍是决定计算精度的关键。选取不同的泵源阻抗模型，对应不同的阻抗拟合函数[13]。分布参数模型考虑了泵源的反共振特性，如图8所示。

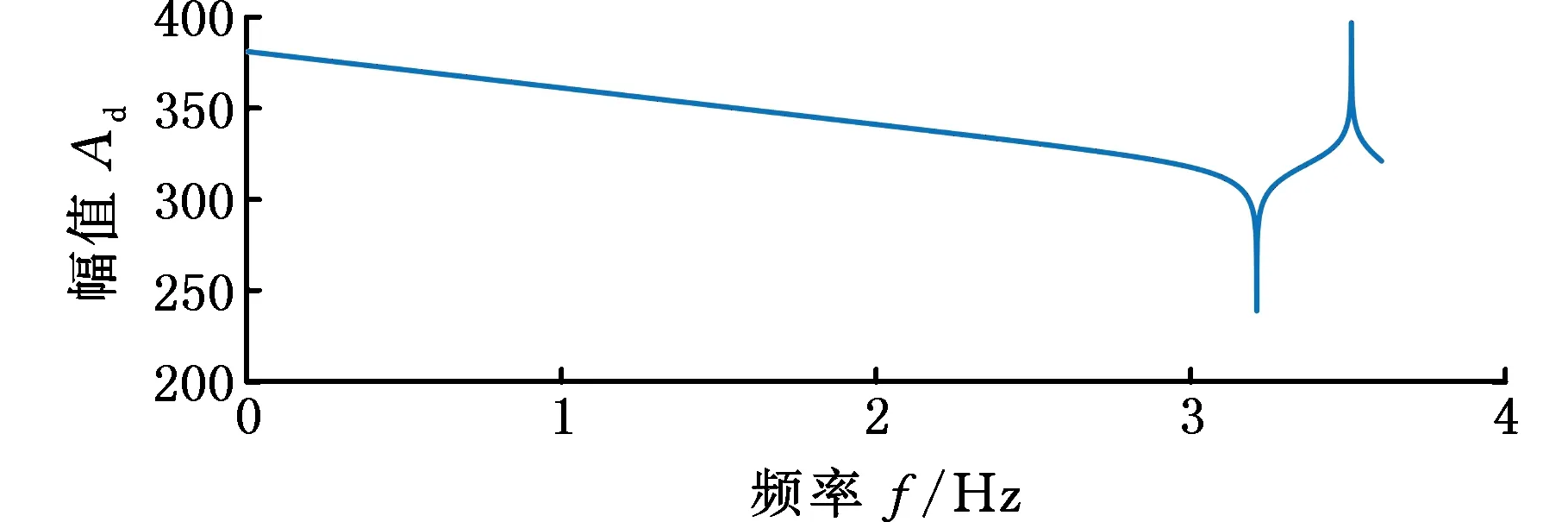
(a)幅值

假定阻抗函数模型为

式中，k1、k2为待拟合常数。

集中参数模型认为泵源阻抗为图9所示的线性函数关系，即

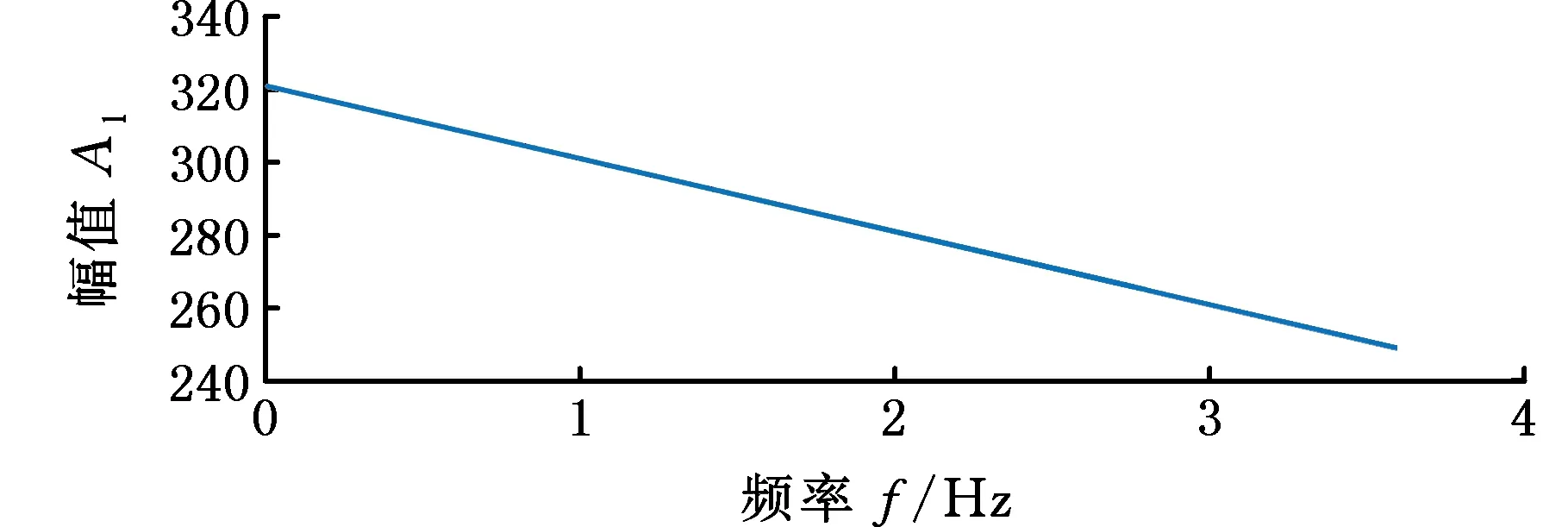
(a)幅值

式中，k3为待拟合常数。

在此基础上宋月超等[18]还提出采用线性衰减法拟合被测泵源全频带上的阻抗值。由于泵源阻抗幅值随频率变化范围广，故直接以拟合点阻抗幅值差值平方最小为目标函数易导致小阻抗幅值点拟合误差过大，甚至掩盖其本身测试数据信息。因此，本文提出采用三次样条插值的加权系数法分段拟合，对于任意测试频段f∈[fi,fi+1](i=1,2,…,n)，拟合函数为

式中，ak,i为待拟合系数。

设定拟合目标函数为

ΔE=i=lnbi(Zst,i-Zsm,i)2

式中，Zsm,i为拟合点；Zst,i为实测点；bi为各分段上的加权系数值。

对于不同频段上的拟合，可通过调整各分段bi值以最小化误差ΔE，获得较优的全频带拟合阻抗曲线。

3 测试步骤

3.1 测试平台搭建

根据上述分析，搭建的流量脉动测试标准平台主要有三部分：被测泵、二次源泵、测试管路。结合推导中所做的假设，以及测试精度影响因素，为提高测试数据的准确性，测试硬件需满足以下条件：

(1)被测泵应安装良好、吸油充分，运行工况可调。被测泵的安装直接决定测试数据能否反映泵源的真实状态，若对中偏差较大则易在系统中产生线谱噪声，若吸油不足则容易吸空，改变了理论中稳态层流的假设条件，因此被测泵需正确安装且运行良好。

(2)二次泵源安装良好，运行谐频点与被测泵谐频点错开。在计算测试主泵源阻抗曲线时，两泵源同时开启，若谐频点重合则被测泵作为负载终端的压力数据将被淹没。

(3)测试管道为长直的硬质管段，管道横截面积尽量无变化，水听器端面与管路内表面尽量取平。

(4)压力传感器以及数据采集设备采样频率尽可能高。若液压泵基频为150 Hz，则分析至十阶线谱即1.5 kHz，设备采样频率至少高于3 kHz。测试平台液压原理如图10所示，建设的实物如图 11所示，选用的元器件参数如表1所示。

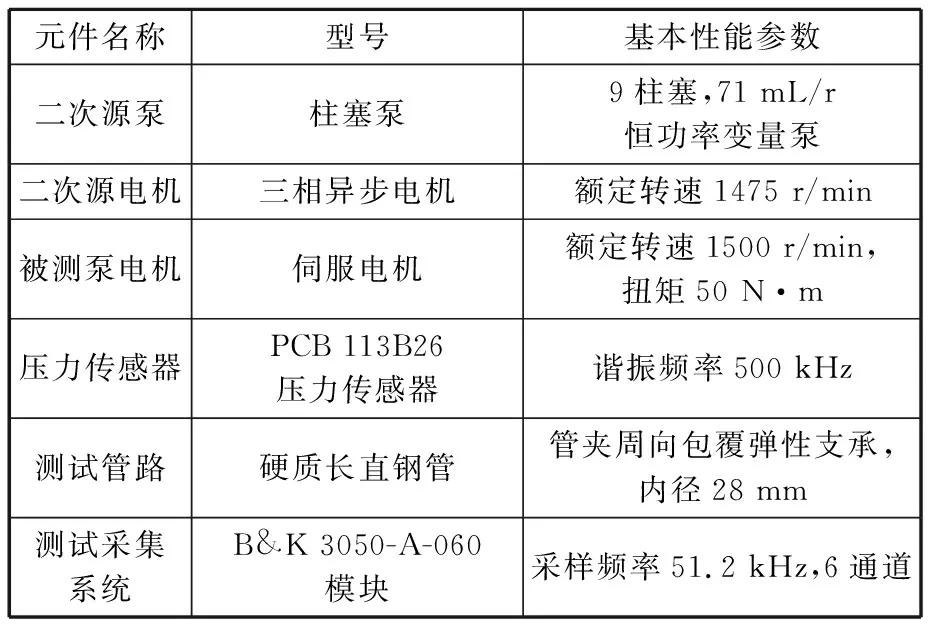
表1 测试平台选用的元器件

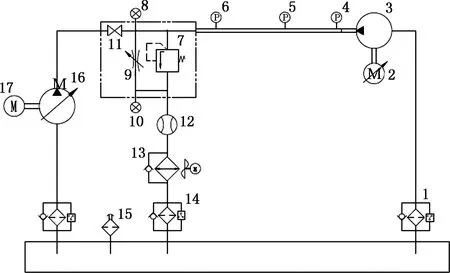
1.过滤器 2.伺服电机 3.被测泵 4～6.压力传感器 7.溢流阀 8.压力表 9.可变节流阀 10.压力表 11.截止阀 12.流量计 13.冷却器 14.过滤器 15.液位显示计 16.柱塞泵 17.三相异步电机

图11 测试平台实物图

3.2 测试步骤及数据处理流程

泵源流量脉动测试流程主要可分为以下几步：

(1)布置水听器数据采集系统，确认试验测试平台各元件连接良好，记录测试台管壁内径、壁厚以及水听器布置位置、油液密度、黏度等基本特性参数。

(2)同时开启被测泵和二次源泵，逐渐调至测试工况。

(3)持续运行一段时间，待系统油温、被测泵转速、出口压力等工况稳定后，记录水听器数据P1t，注意观察二次源泵和被测泵线谱是否重叠。

(4)关闭二次源泵，关闭对应截止阀11，调整可变节流阀9的开口，使其出口压力恢复至测试工况下的出口压力P，待运行稳定后，记录水听器数据P2t。获取相应试验数据后，试验数据完整处理流程如图12所示[18]。

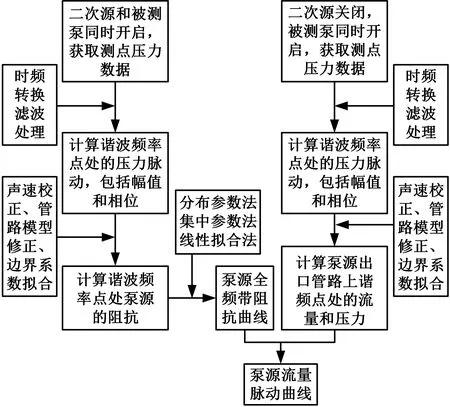
图12 流量脉动数据处理流程

试验数据处理过程较为复杂，涉及相关专业知识，过程耗时长，不利于工程化应用。为简化流程，编译了测试数据处理软件，其界面如图13所示。

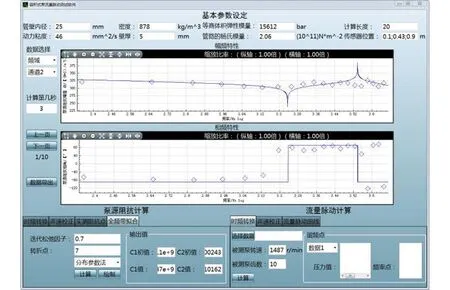
图13 流量脉动测试软件界面

软件基于C语言编写，可运行在不同操作系统平台上，方便测试人员及时分析数据，了解测试数据的有效性和结果的准确性。软件分为了三大区域，软件上部为基本参数设定区域；中部为数据曲线显示区，方便直观地看到测试结果；下部为计算步骤选择区。下部的计算步骤选择区按照数据处理流程给出，分为以下几个部分：

(1)泵源阻抗计算。①时频转换，读取记录的数据P1t，将原始数据由时域转化至频域；②声速校正，基于三测点间声速相等修正该工况下的声速和管路弹性模量；③实测阻抗点，获取二次源泵谐频点处的压力数据，计算该点阻抗；④全频带阻抗拟合，基于各点阻抗拟合全频带阻抗。

(2)流量脉动计算。①时频转换，读取记录的数据P2t，将原始数据由时域转化至频域；②声速校正，基于三测点间声速相等修正该工况下的声速和管路弹性模量；③流量脉动曲线，获取被测泵谐频点处的压力数据，根据泵源阻抗得到流量脉动曲线。

4 测试结果

4.1 数据计算流程

以被测泵1200 r/min稳定运行、出口压力5 MPa工况为例，采用上述数据处理软件，给出详细计算步骤。数据采集系统获取的P1t和P2t原始数据以及经滤波、时频变换得到的曲线分别如图14～图17所示，提取频域上前20阶线谱的压力脉动值P1f、P2f。根据基本边界条件参数，利用得到的前20阶压力脉动幅值，分别计算二次源开启前后测试工况下的声速和有效弹性模量，如表2所示。

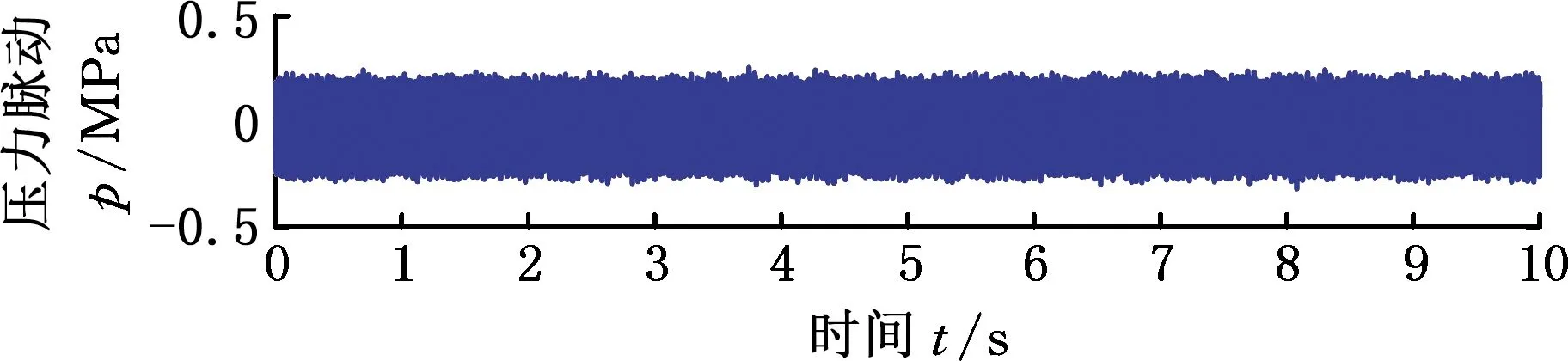
(a)1号测点

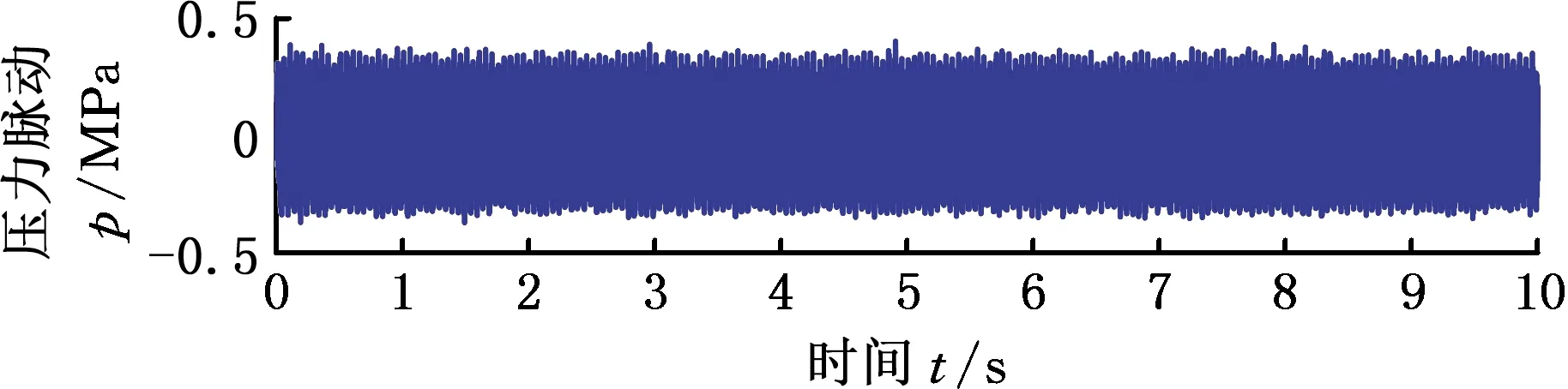
(a)1号测点

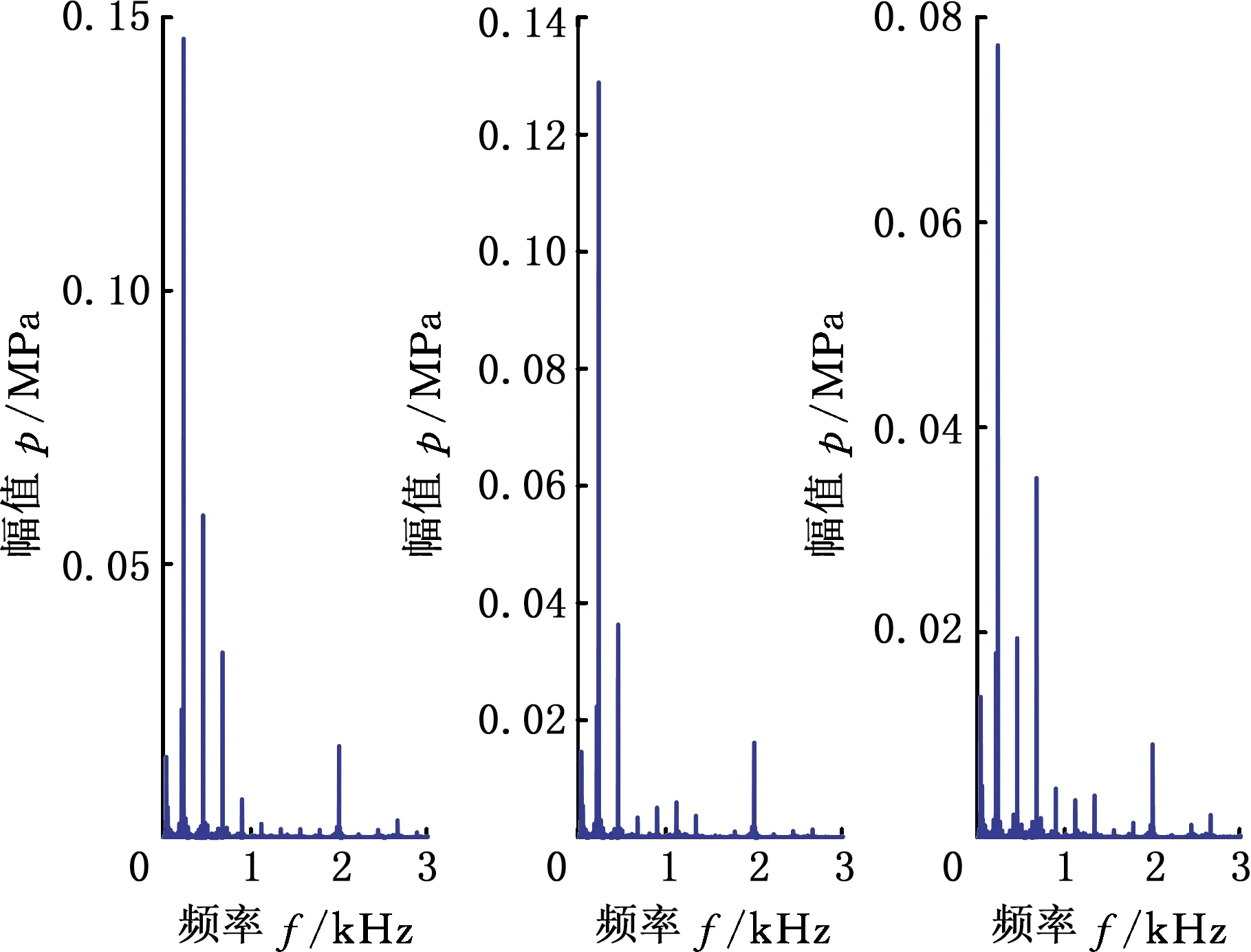
(a)1号测点 (b)2号测点(c)3号测点

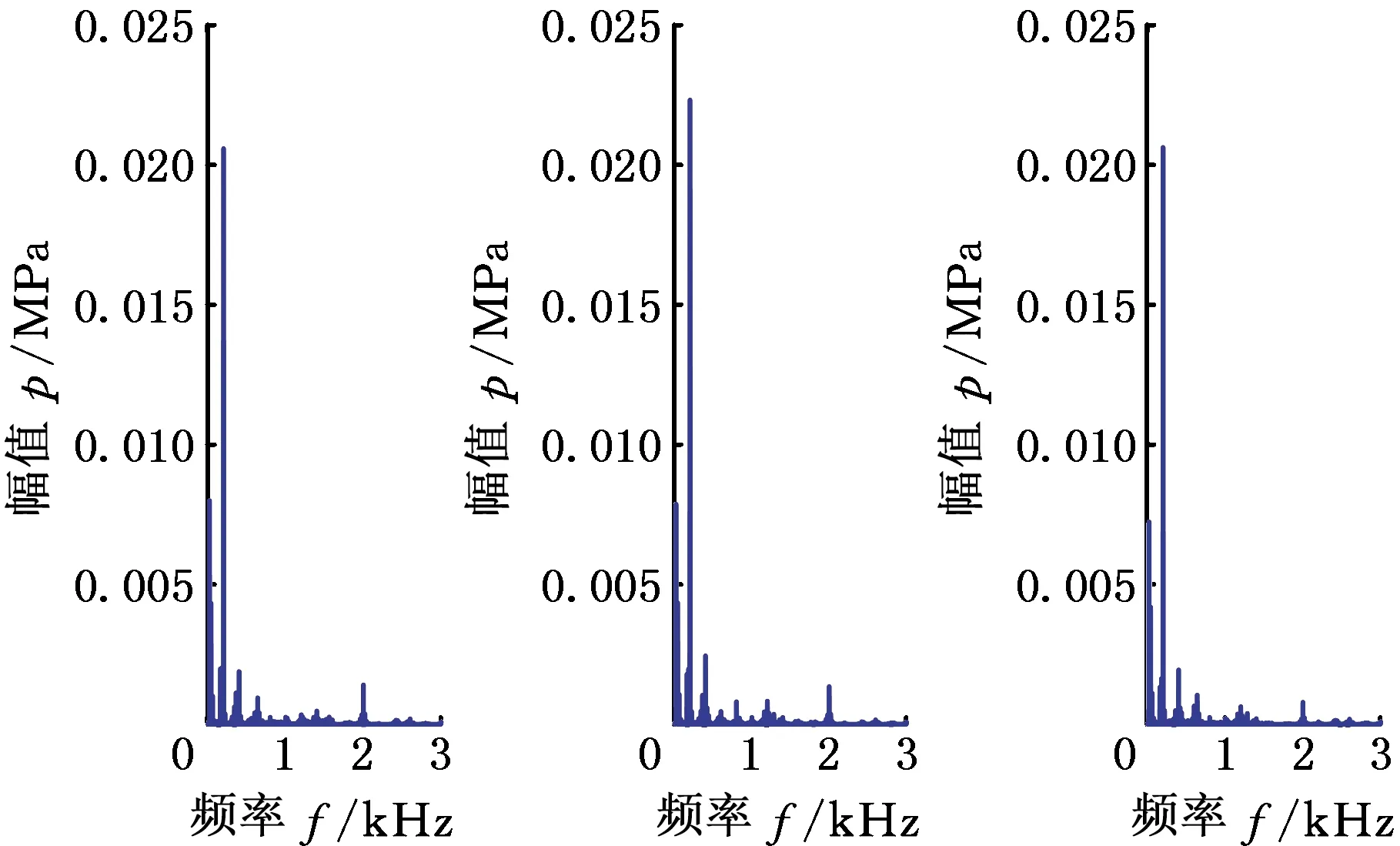
(a)1号测点 (b)2号测点(c)3号测点

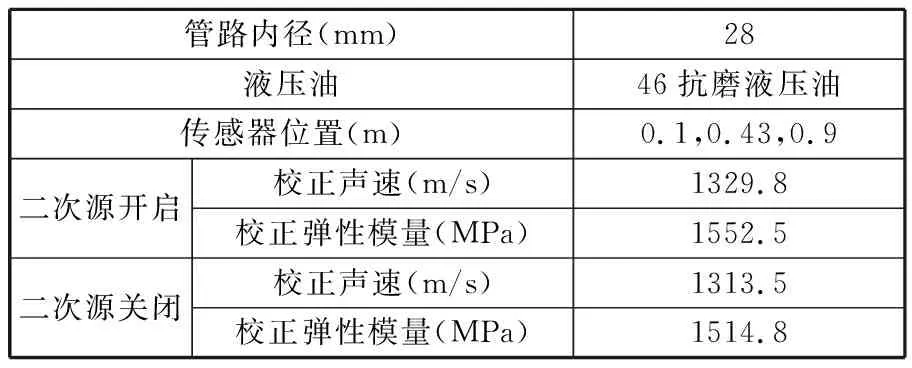
表2 基本边界参数

根据P1f求解得到二次源泵频率点处被测泵的阻抗，拟合得到被测泵全频域范围内的阻抗特性，计算得到阻抗点和拟合后的阻抗曲线见图18和图19所示。利用该工况下被测泵全频带阻抗值，结合P2f计算得到各脉动频率点流量脉动的幅值及其相位，如图20所示。将频域数据反变换可得流量脉动时域曲线：

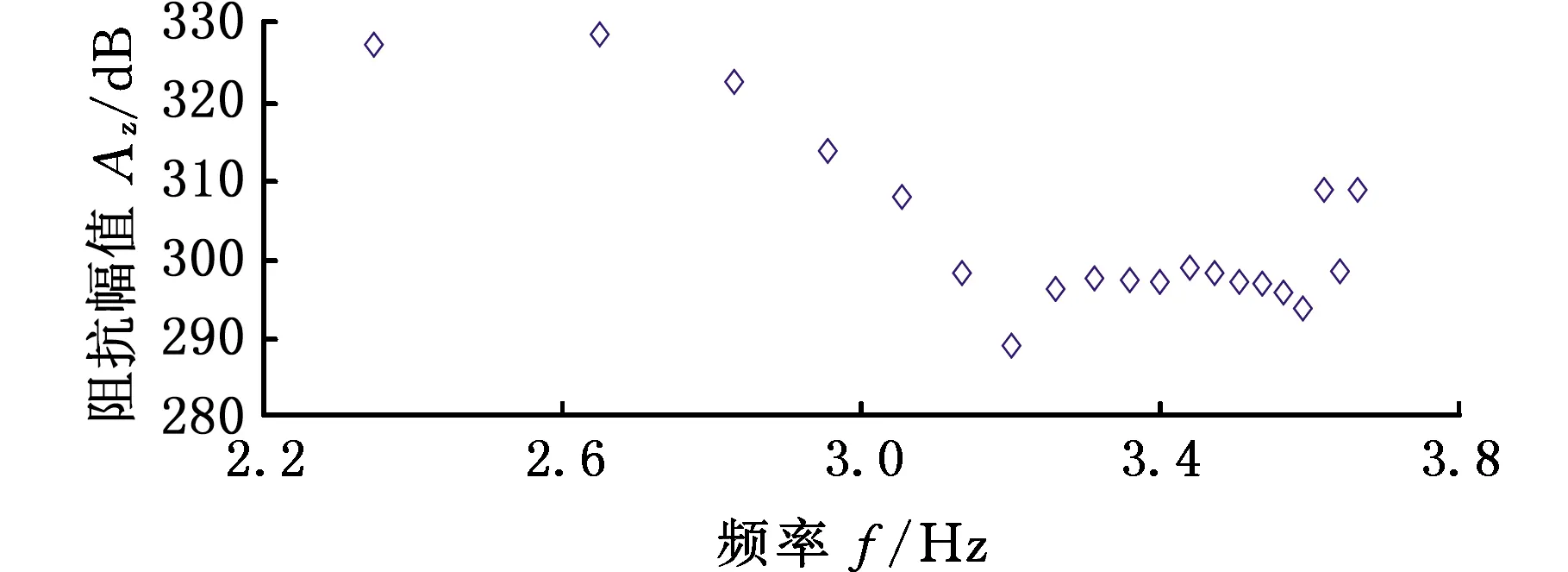
(a)幅频特性

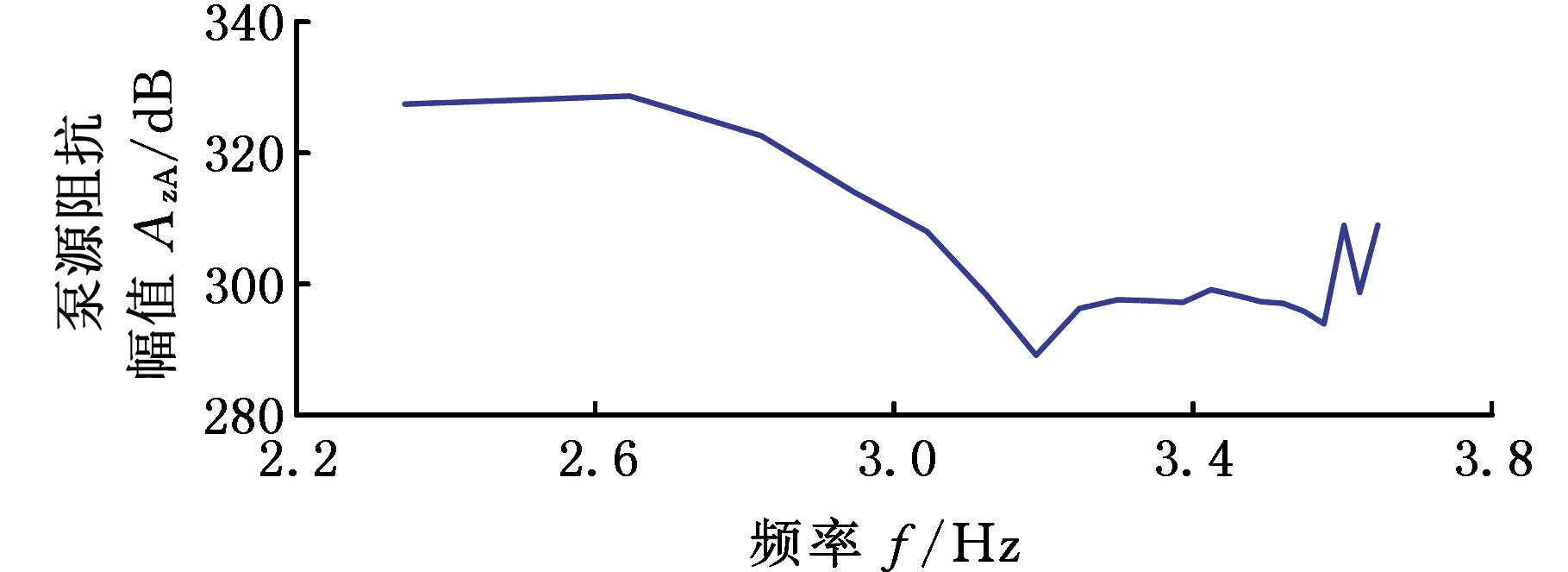
(a)幅频特性

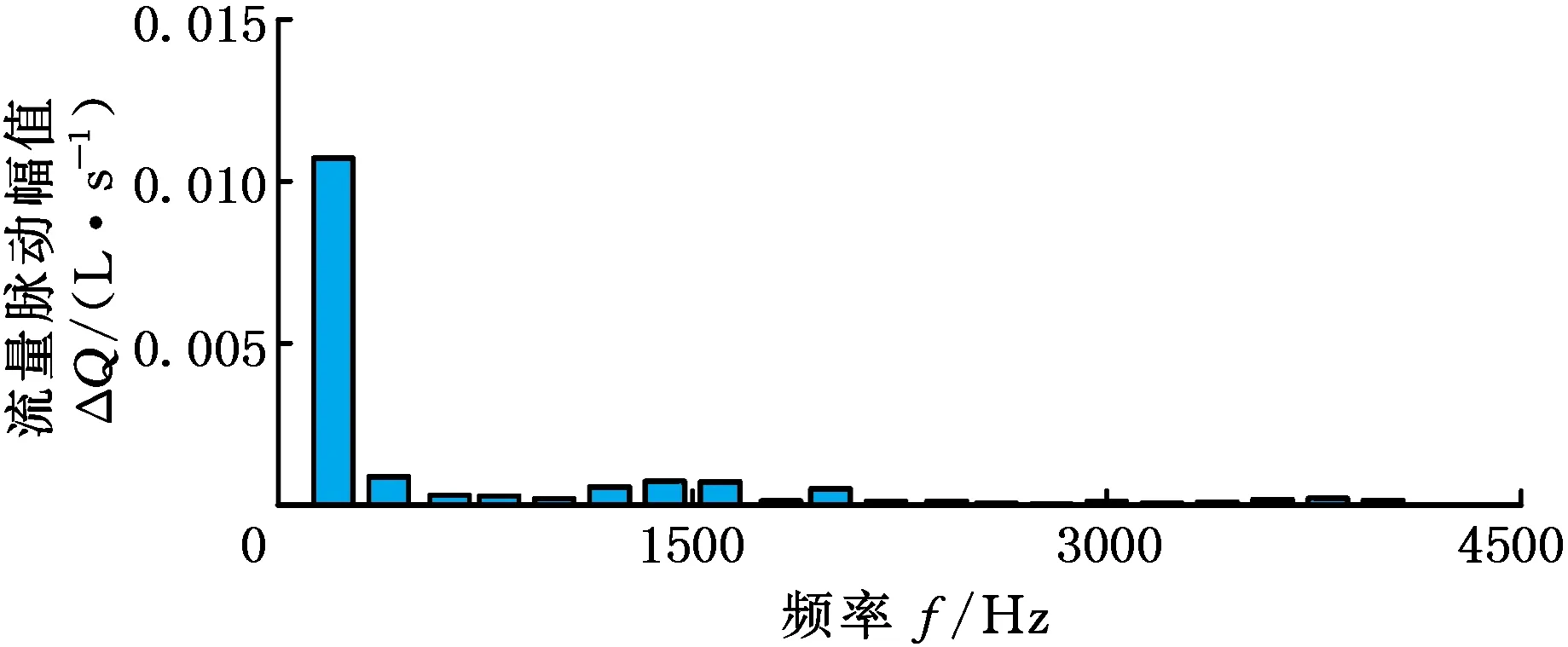
(a)幅值

最终得到的流量脉动曲线见图21。通过以上数据处理流程可知：①编译的数据处理软件有效可行，能够根据测试数据计算出该工况下泵源的流量脉动；②二次源开启前后，校正得到的声速和弹性模量略有差异,且二次源开启时，声速快、有效体积弹性模量大，这是二次源开启时管路中流量增大所致，与实际情况相符，表明通过声速和弹性模量校正算法能够充分考虑测试工况提高计算结果的精度；③直线共轭内啮合齿轮泵的输出流量脉动以一阶线谱成分为主，其他高阶频率处的脉动几乎可忽略。

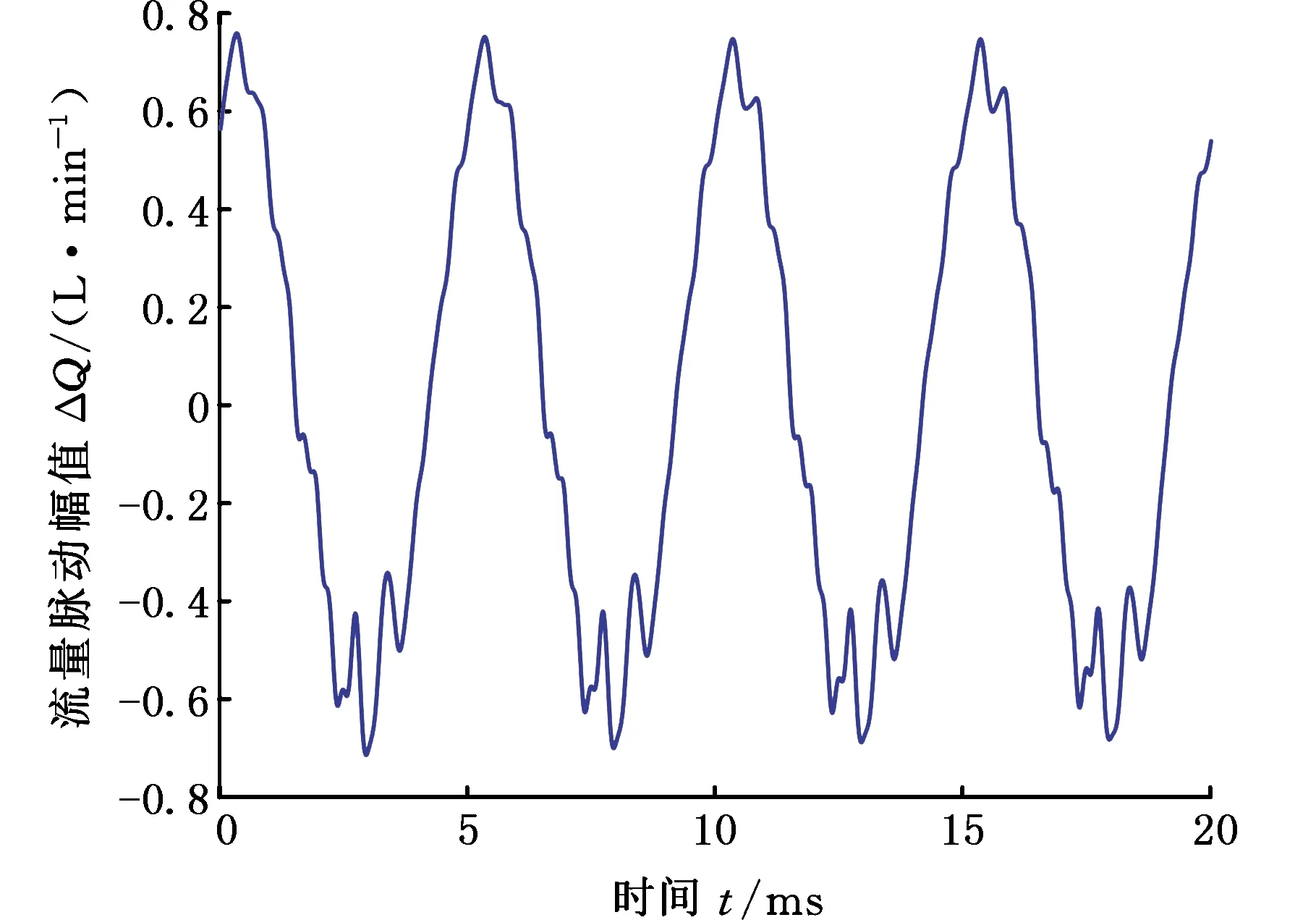
图21 泵源出口流量脉动幅值

4.2 不同拟合算法对比

相比于线性插值法，本文采用的加权系数法拟合曲线更光顺，更能反映出泵源阻抗的反共振点。如图22所示，在反共振点阻抗幅值达到最小，相位恰好由负变为正，相同的流量脉动激励，此频率点处将产生更小的压力脉动。实际系统设计时，应尽量让液压泵稳定运行的基频点靠近此点[19]，降低输出压力脉动。

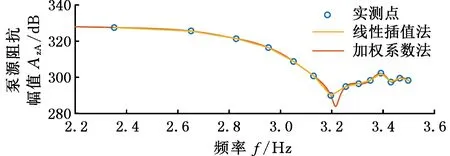
(a)幅频特性

4.3 实测值与理论值对比

被测直线共轭内啮合齿轮泵基本结构如图23所示，其主动轮齿数为10，因此其理论流量脉动周期为36°。理论排量为25.1 mL/r，设计工况为12.5 MPa，1200 r/min。根据齿轮泵的几何结构形式，数值计算可得其理论流量脉动曲线，数值计算过程中存在以下几点假设：①油液为理想液体，忽略油液的压缩性；②液压泵无泄漏，容积效率为100%；③无卸荷槽，不存在卸荷作用。实际工况下，压力越高，油液压缩越大，泄漏量越大，卸荷槽的卸荷作用越明显，引起出口流量脉动的幅值波动越大。因此可以预计，在低压测试工况下理论值与实测值一致性较好，高出口压力下误差将逐渐增大。不同压力运行工况下，理论流量脉动曲线与实测曲线对比如图24～图28所示。

图23 直线共轭内啮合齿轮泵结构形式

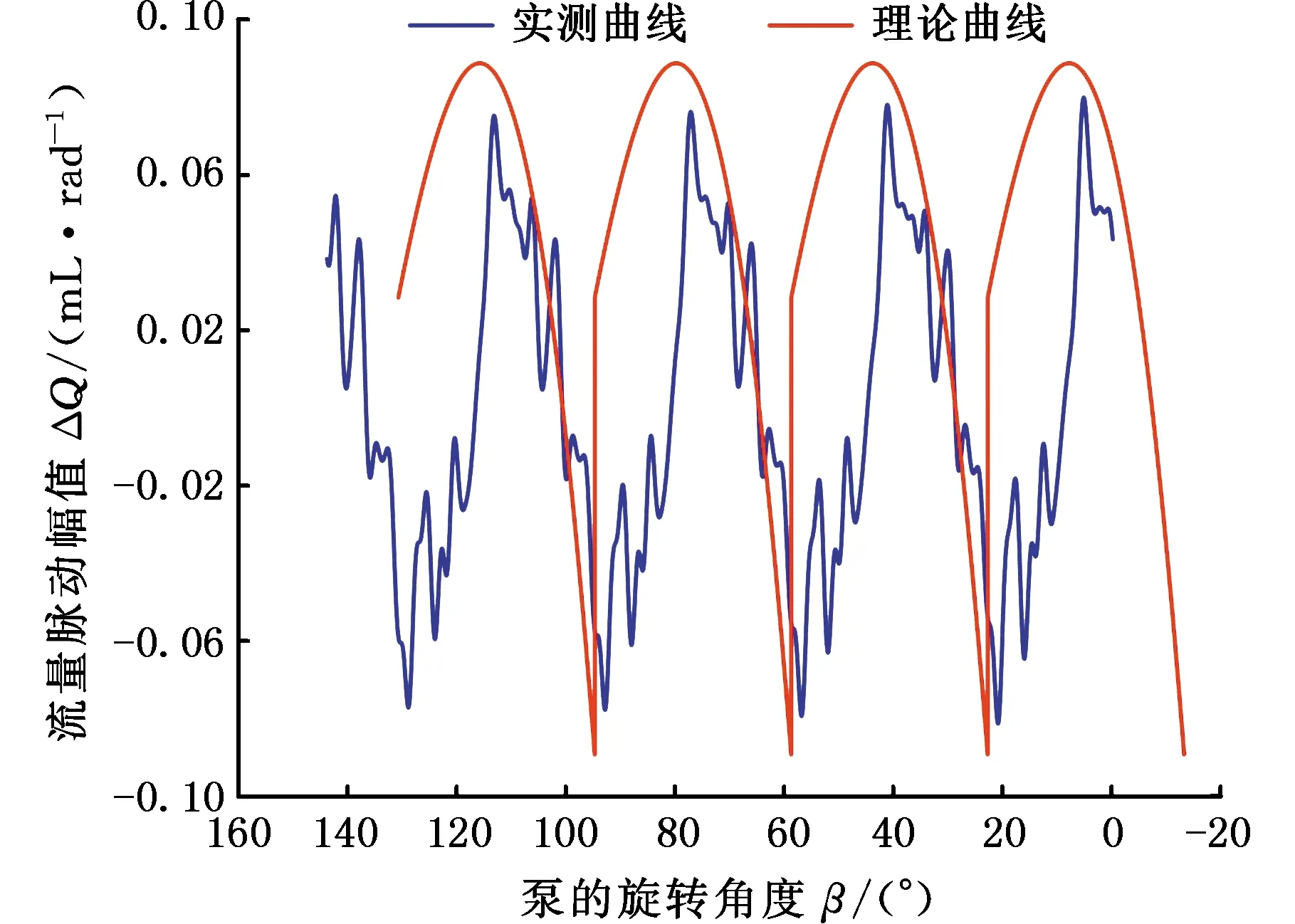
图24 2 MPa测试数据与理论曲线

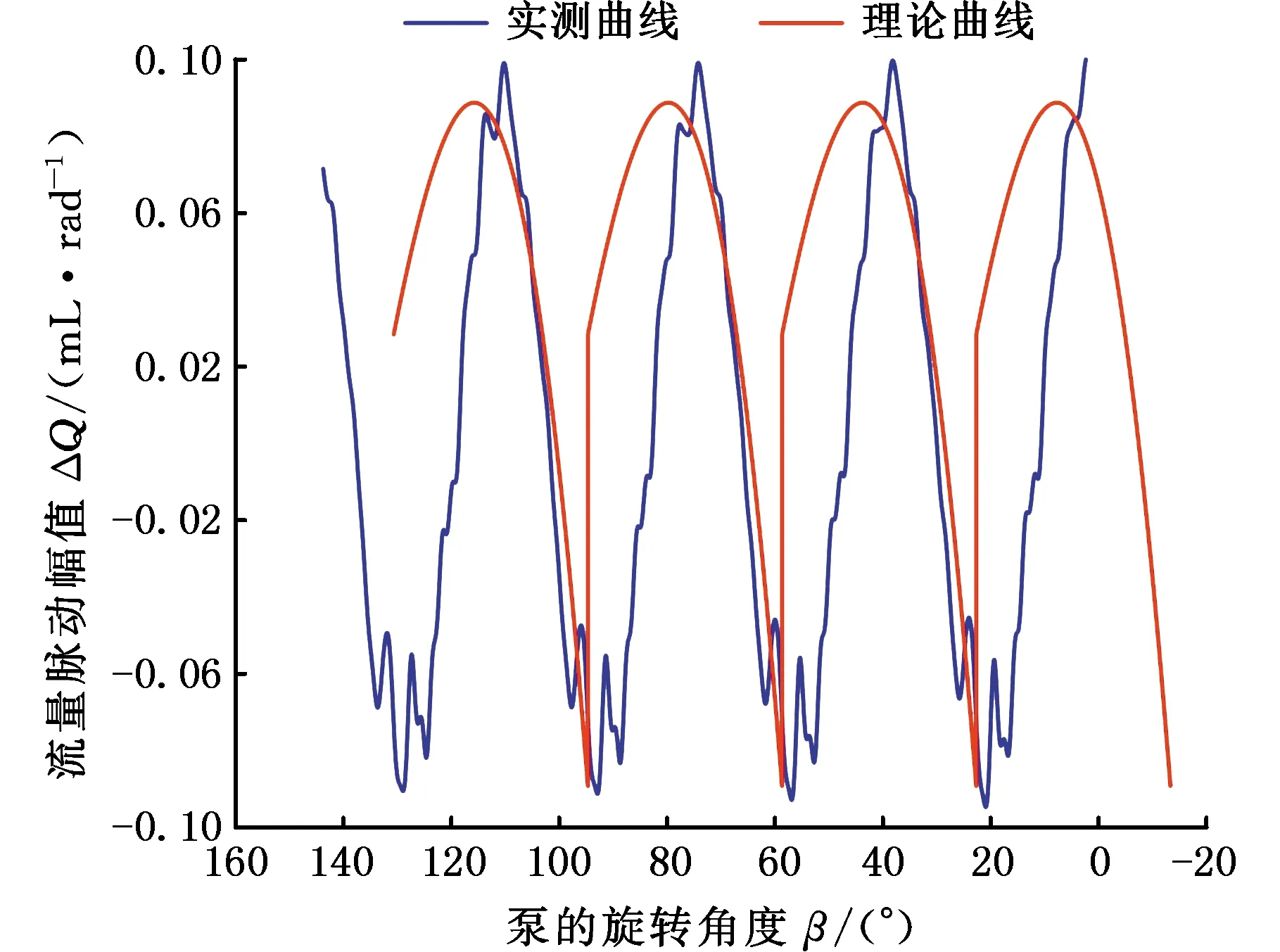
图25 5 MPa测试数据与理论曲线

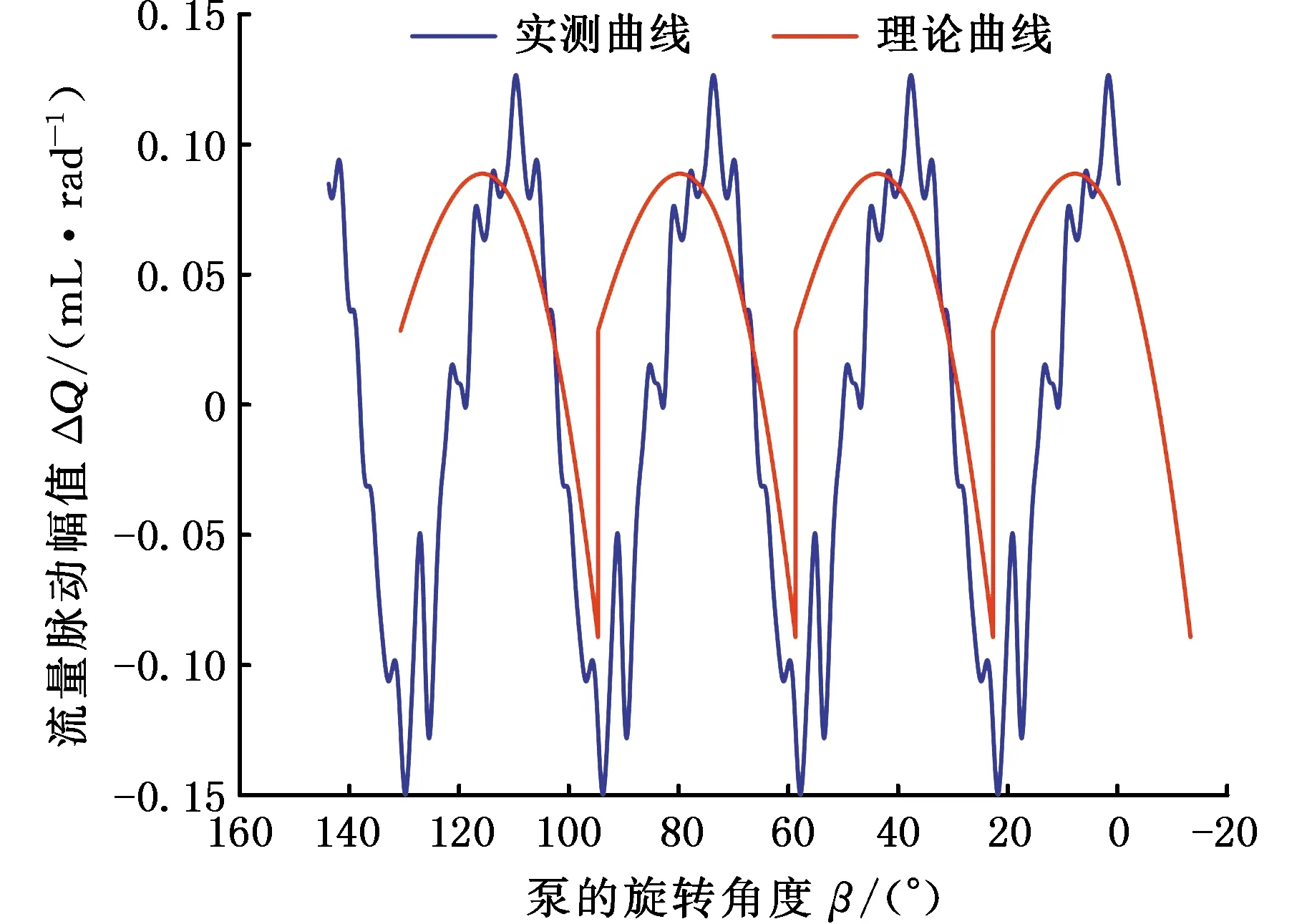
图26 7.5 MPa测试数据与理论曲线

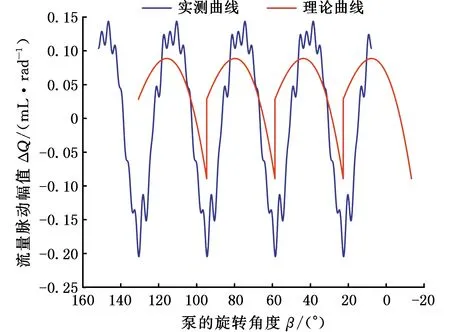
图27 10 MPa测试数据与理论曲线

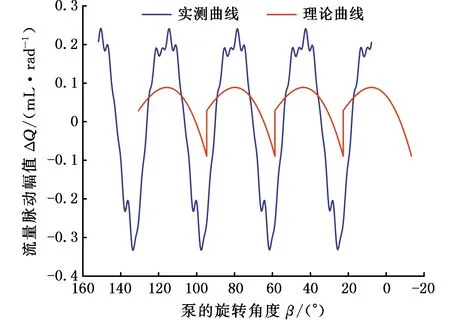
图28 12.5 MPa测试数据与理论曲线

根据对比结果，可得以下结论：①该测试方法和数据处理流程准确可行，能够测试出不同工况下泵源出口流量脉动值[20]；②理论流量脉动曲线与实测流量脉动曲线变化趋势和曲线形状相似，流量脉动周期均为36°；③在高出口压力工况下，理论流量脉动幅值与实测流量脉动幅值差别较大，与预期效果一致。出口压力越小，油液压缩性越小，泄漏量越小，流量脉动曲线匹配的一致性越好。随着出口压力增大，油液压缩变大，泄漏增大，导致实测流量脉动幅值与理论值的匹配误差也越大。

4.3 不同运行工况对比

测试该泵在不同转速、不同出口压力下出口流量脉动幅值和流量脉动率，得到其变化趋势如图29所示。

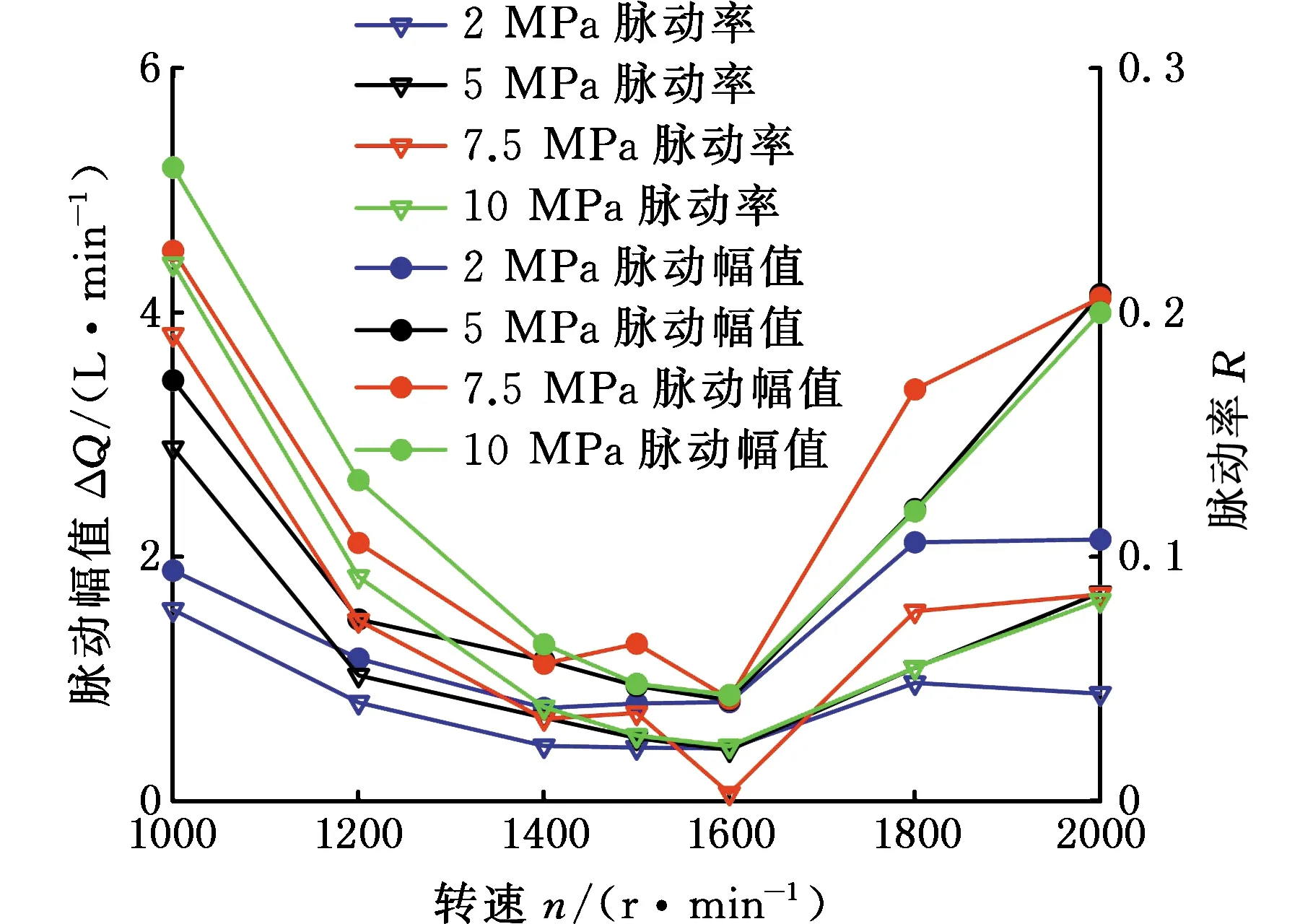
图29 不同工况下实测流量脉动幅值及脉动率

测试结果反映出直线共轭内啮合齿轮泵流量脉动幅值随转速先减小后增大，随出口压力升高而增大；计算过程中也反映出，各工况下该直线共轭内啮合泵的流量脉动特征均以一阶线谱为主，高次谐频处的流量脉动幅值相对较小[21]。

5 结论

本文推导了二次源法流量脉动的测试原理，讨论了测试精度的影响因素，给出了提高测试精度的方法和建议；分析了测试数据的处理方法，编译数据处理软件实现了测试的程序化和标准化。以直线共轭内啮合齿轮泵为研究对象，实际测试了泵源出口的流量脉动，得出以下结论：

(1)管路模型的简化方法、油液体积弹性模量、压力传感器安装方法以及阻抗数据拟合方法等多种因素均可能对流量脉动的最终测试结果产生影响，有效的处理方法可提高测试精度。

(2)本文采取的流量脉动数据处理方法准确可行，能够用于液压泵的输出流量脉动测试；采用的加权系数法能够很好地反映泵的反共振特性，可用于泵源的阻抗拟合中。

(3)该型直线内啮合齿轮泵流量脉动幅值随转速的增大先减小后增大，随出口压力升高而增大，高转速下输出流量更平稳；流量脉动特征以一阶线谱为主，高次谐频处的流量脉动幅值可忽略。