地震作用下组合梁斜拉桥刚度配置及合理体系研究

张世冀, 贾少敏

(1.贵州省交通规划勘察设计院股份有限公司, 贵州 贵阳 550001； 2.四川农业大学, 四川 成都 611830)

0 引言

随着我国“交通强国”、“西部大开发”战略的提出，高墩组合梁斜拉桥在我国山多沟深的西部地区得到充分发展。但我国是地震多发国家，探究地震作用下组合梁斜拉桥刚度配置和合理体系，不仅可以提高斜拉桥使用寿命和行车舒适性，还可以减小工程造价。

学者们对斜拉桥的抗震探究也不计其数。陈应高[1]等以贵州山区某世界级斜拉桥为研究背景，基于时程分析法探究了山区斜拉桥在地震作用下的合理体系，并对粘滞阻尼器的关键性参数进行了分析。夏修身[2]等基于OpenSees和Sap2000建立了中等跨度斜拉桥的动力分析基准模型，提出斜拉桥拉索初始应变的计算方法。MARTNEZ-RODRIGO[3]等探究了4种不同减隔震装置下某斜拉桥在纵向地震作用下的抗震性能，研究表明黏滞阻尼器可以最大限度地减小斜拉桥地震响应。杨庸[4]等研究了斜拉索重叠布置、塔间斜拉索、提高桥塔刚度等参数对三塔斜拉桥力学行为的影响规律，但仅局限于静力下的计算，并未考虑形如地震等动力作用下的计算。SHAHRIA ALAM[5]和RAHMAN BHUIYAN[6]等探究了强震作用下不同弹性橡胶隔震支6座参数对桥梁地震响应的影响规律。姜冲[7]、方圆[8]、詹建辉[9]等从影响斜拉桥关键控制性能的参数角度出发，探究了各参数对斜拉桥受力情况的影响，但未考虑地震荷载的影响。PENG[10]等和刘振标[11]等探究了某钢箱混合梁斜拉桥在静力、汽车荷载、地震以及风环境作用下的受力问题。李天恩[12]介绍了矮塔斜拉桥在受力性能、抗疲劳以及铁路建设领域的优势，也从主梁刚度角度探究了其抗风性能。张海[13]等以某矮塔斜拉桥为研究对象，对体系的约束、支座、锚固等进行了研究，但未涉及整体受力及抗震性能的计算。

基于上述研究，本文以贵州某高墩组合梁斜拉桥为研究对象，研究地震作用下不同塔墩高度、不同塔梁刚度和不同约束体系对塔顶位移、塔底内力以及主梁跨中挠度的影响，为同类桥梁设计做参考。

1 工程背景及有限元模型

本文以贵州省某特大组合梁斜拉桥为工程背景，探究地震作用下组合梁斜拉桥刚度配置及合理体系。全桥长1 697.5 m，桥梁主梁为(72+212+560+212+72)m 双塔双索面组合梁斜拉桥，桥宽27.5 m。主桥约束方式为：组合梁在索塔下横梁上设置竖向支承，辅助墩、交界墩与桥台上设置竖向支承。主梁为钢-混组合梁。钢主梁为双工字型截面，砼桥面板厚28 cm，工字形主梁上翼缘版顶部加厚50 cm，主梁全宽27.5 m，其桥型布置见图1。

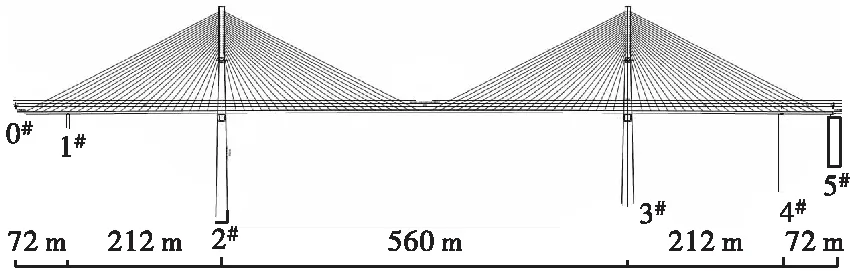
图1 桥型布置图

2#(高288 m)和3#(高268 m)桥塔均为菱型C50桥塔，采用矩形空心截面。每个上塔柱均布置了22对斜拉索，上部20对斜拉索采用钢锚梁锚固形式。

本文基于Sap2000建立有限元模型，通过改变桥墩高度、塔梁连接方式和塔梁刚度，以此探究地震作用下斜拉桥刚度配置及合理体系研究，其有限元模型原型见图2，原体系塔梁处采用半漂浮体系，基础固结，桥台、辅助墩及交接墩释放纵向约束。

图2 斜拉桥有限元模型

2 地震动确定

本文按表1所选的7条实测地震作为有限元模型的地震激励，选取依据是根据该桥所在桥址处地震特征，并结合规范得到的规范目标反应谱。

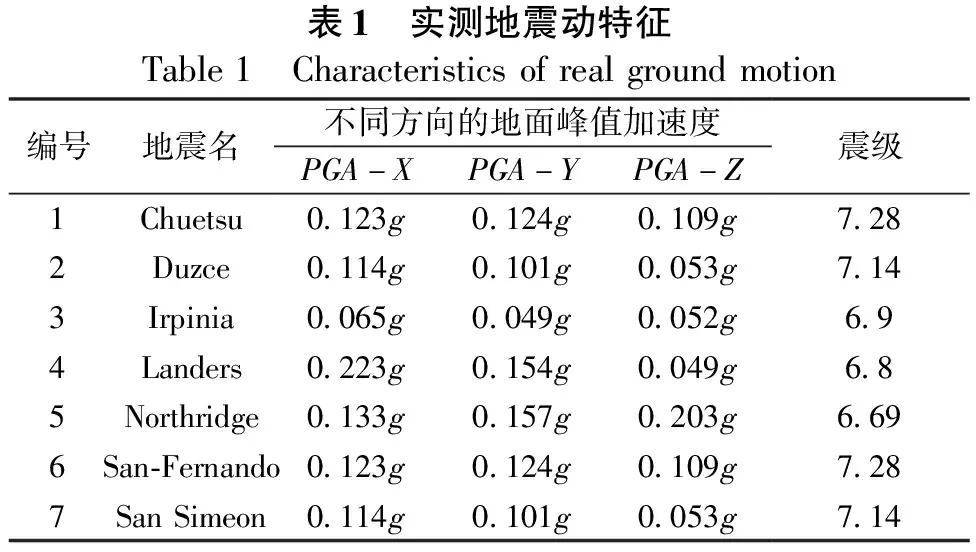
表1 实测地震动特征Table1 Characteristicsofrealgroundmotion编号地震名不同方向的地面峰值加速度PGA-XPGA-YPGA-Z震级1Chuetsu0.123g0.124g0.109g7.282Duzce0.114g0.101g0.053g7.143Irpinia0.065g0.049g0.052g6.94Landers0.223g0.154g0.049g6.85Northridge0.133g0.157g0.203g6.696San-Fernando0.123g0.124g0.109g7.287SanSimeon0.114g0.101g0.053g7.14

3 自振特性分析

结合有限元中桥梁结构自由振动基本特性的相关算法，得出该斜拉桥前10阶的振动频率和振型描述见表2。

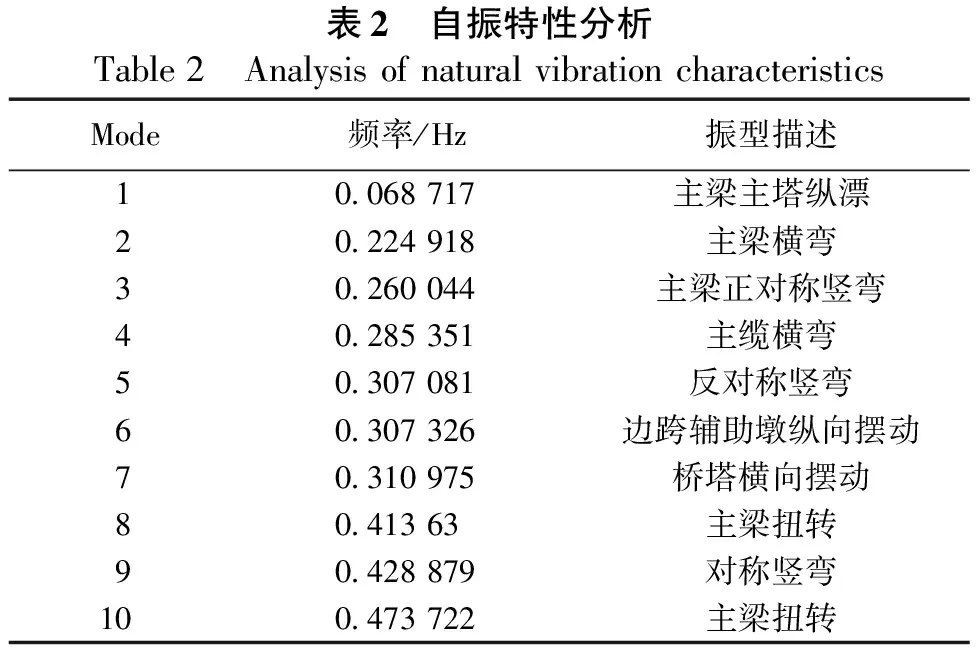
表2 自振特性分析Table2 AnalysisofnaturalvibrationcharacteristicsMode频率/Hz振型描述10.068717主梁主塔纵漂20.224918主梁横弯30.260044主梁正对称竖弯40.285351主缆横弯50.307081反对称竖弯60.307326边跨辅助墩纵向摆动70.310975桥塔横向摆动80.41363主梁扭转90.428879对称竖弯100.473722主梁扭转

4 地震响应分析

4.1 桥墩高度变化

2号和3号索塔总高分别为288 m和268 m，其中上塔柱高71 m，中塔柱高77 m，下塔柱高55.5 m，2号和3号塔墩高分别为84.5 m和64.5 m。可见两个桥塔均为超高墩桥塔，为研究桥墩高度对高墩多塔斜拉桥静力特性的影响，保持除墩高外的结构参数不变，分别建立2个塔墩的高度都增加30、20、10、0(原塔墩体系)、-10、-20和-30 m的有限元模型，以此考察地震作用下塔顶位移、塔底弯矩和跨中挠度的变化情况，此处负号表示在原体系上减小相应数值的塔墩高度。

a.塔顶位移。

在两种地震组合方式(纵+竖、横+竖)下的两个塔顶变位分别见图3和图4。图3和图4中2#(横向+竖向地震)表示在横向+竖向地震作用下2#塔顶的结构响应，其余类推。

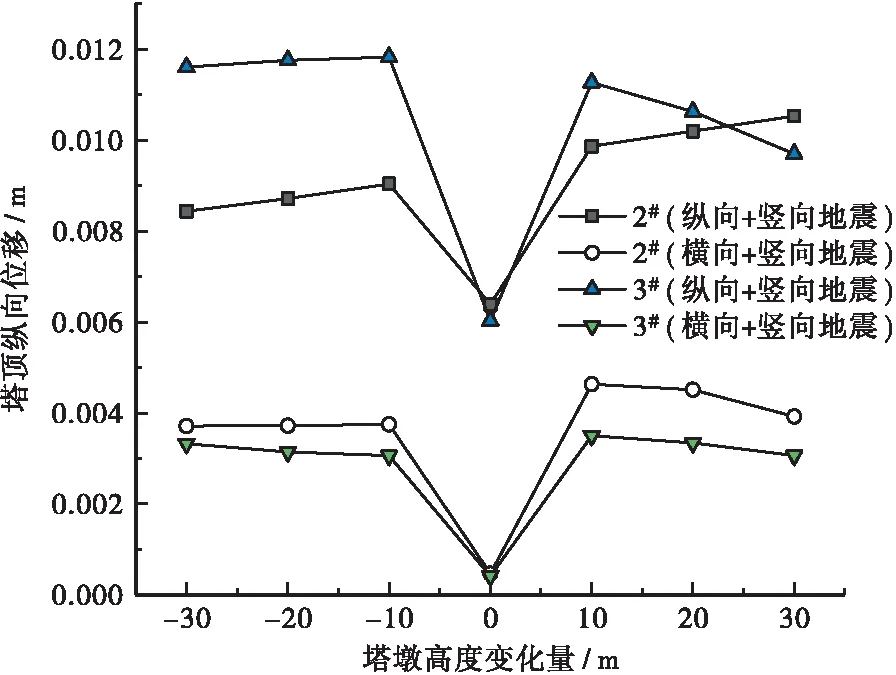
图3 塔顶纵向位移

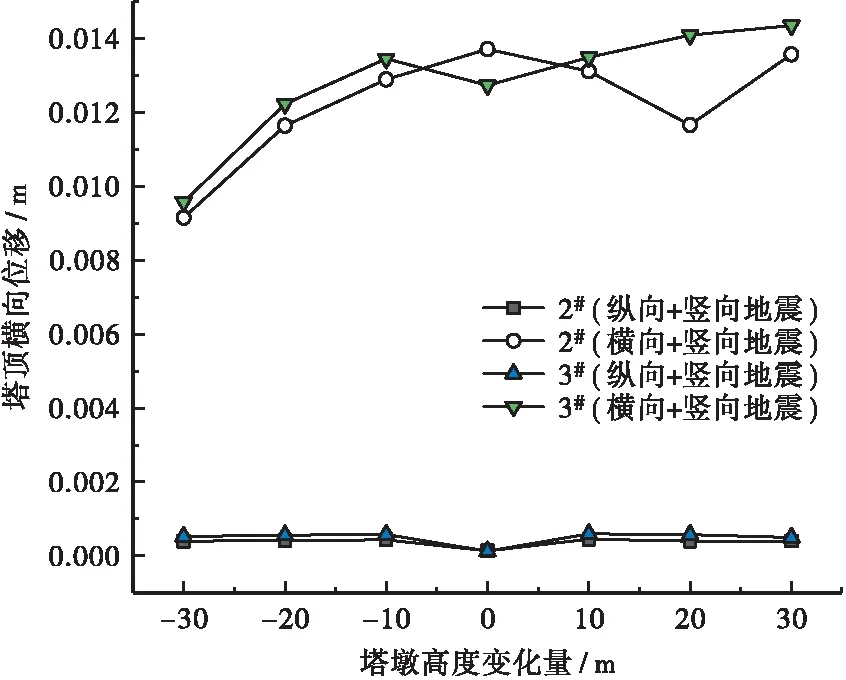
图4 塔顶横向位移

据图3可知，在纵向+竖向地震作用下塔顶纵向位移要大于塔顶横向位移，塔墩高度不增加时的2#和3#塔横向位移均为零，且此时的纵向位移也最小，因此从塔顶纵向位移角度考虑，原塔墩高度体系最为合理。

据图4分析可知，当塔墩高度减小30 m时，在横向+竖向地震作用下的塔顶横向位移最小，约为0.011 m。纵向+竖向地震下的塔顶横向位移基本为零，除了原体系，但此时位移也较小，为0.014 m。2#和3#塔顶横向位移在横向+竖向地震作用下随塔墩高度增加而增加。因此，从塔顶横向位移角度而言，塔墩高度可在原体系上调整±20 m。

b.塔底内力。

2#和3#塔底内力在两种地震组合方式下随塔墩高度的变化规律见图5和图6。

分析图5和图6可知，2#和3#塔底内力整体上随塔墩高度增加而增加。2#塔底内力以及3#在横向+竖向地震下塔底内力在原体系处增加有所减缓，结合塔顶位移而言，原体系塔墩高度更为合理。

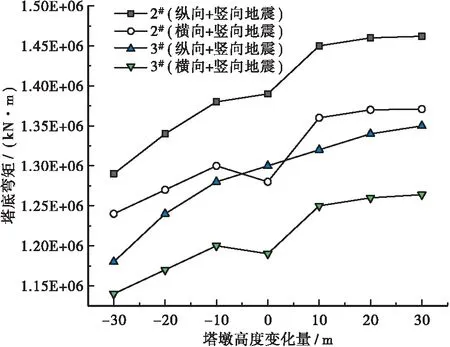
图5 塔底弯矩

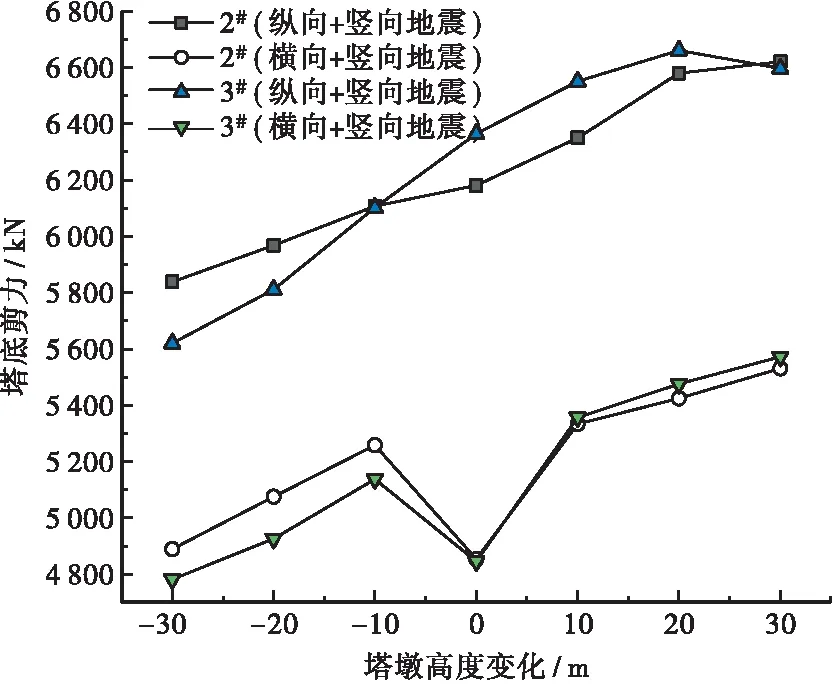
图6 塔底剪力

c.跨中挠度。

主梁跨中竖向挠度在纵向+竖向地震和横向+竖向地震作用下随塔墩高度增加的变化 情况如图7所示。据此分析可知，横向+竖向地震作用下的跨中挠度要大于纵向+竖向地震作用下的跨中挠度，这是由该桥的自振特性决定的。两种地震输入方式下的跨中挠度均在原体系处取得最小值，可见此时的塔墩高度最为合理。

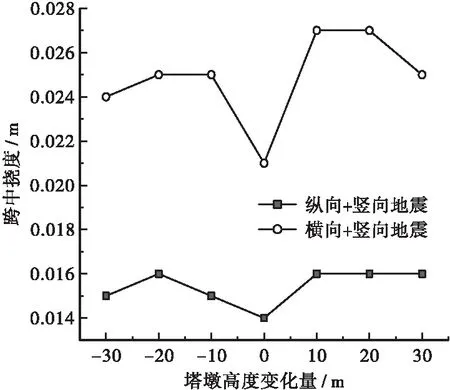
图7 跨中挠度

4.2 塔梁连接方式变化

塔梁约束方式对斜拉桥的力学性能和动力特性有着显著的影响，本文所选桥梁原型主桥采用半漂浮体系。保持桥台、辅助墩约束情况不变，2个塔梁处均改变相同的连接方式，以此探究地震作用下不同约束体系对斜拉桥内力及变形的影响问题。

本文设置3种斜拉桥体系，体系1为全漂浮体系；体系2为桥塔、主梁和塔墩三者进行固结；体系3为半漂浮体系，其约束情况见表3。

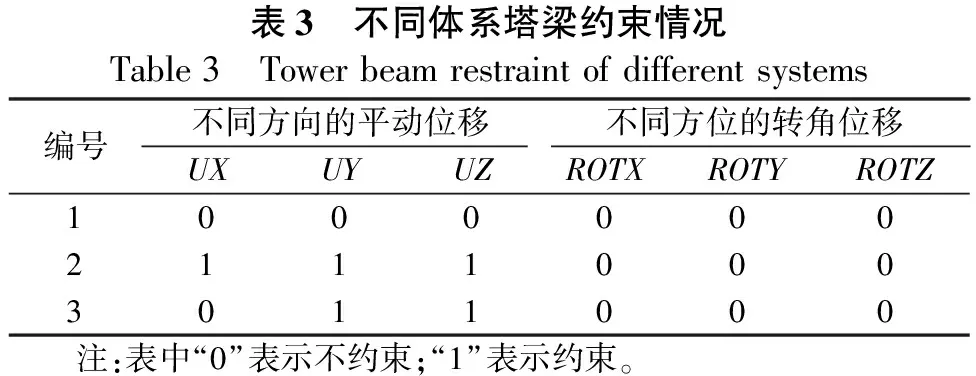
表3 不同体系塔梁约束情况Table3 Towerbeamrestraintofdifferentsystems编号不同方向的平动位移不同方位的转角位移UXUYUZROTXROTYROTZ100000021110003011000 注:表中“0”表示不约束;“1”表示约束。

a.塔顶位移。

3种设计约束体系下的塔顶纵向位移和塔顶横向位移在两种地震输入方式下的变化规律分别如图8和图9所示。

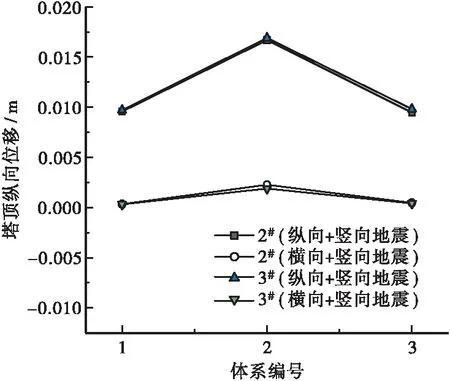
图8 塔顶纵向位移

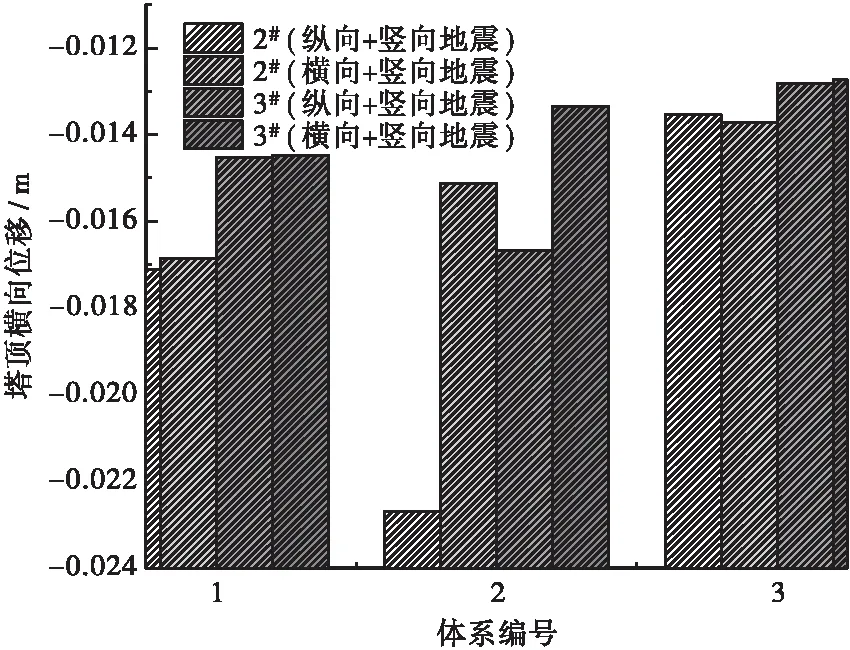
图9 塔顶横向位移

据图8分析可知，纵向+竖向地震下的2#和3#塔顶纵向位移均要大于横向+竖向地震下的塔顶纵向位移，这是因为纵向激励下会激起桥梁的纵向振动，因此纵向位移大于横向位移，反之亦然。体系2下的塔顶纵向位移要大于另外两种体系，这是因为塔梁固结后，塔梁具有相同的变形，而主梁在纵向地震作用下振动较大，因此出现该现象。

据图9分析可知，体系3下的塔顶横向摆动幅度最小，体系1下的塔顶横向位移最大，而体系2下塔顶横向位移略大于体系1。综合图8和图9可知，半漂浮体系为最优选择，但体系2的塔顶摆动位移不是很大，也可考虑。

b.塔底内力。

3种体系下的塔底内力见图10、图11，分析可知，体系2下的塔底内力均小于另外两种体系，这是因为固结后，主梁振动带动桥塔振动，导致桥塔内力较小。而其他两体系变形小，因此桥塔内力大。从塔底内力角度而言，体系2为最佳合理体系。

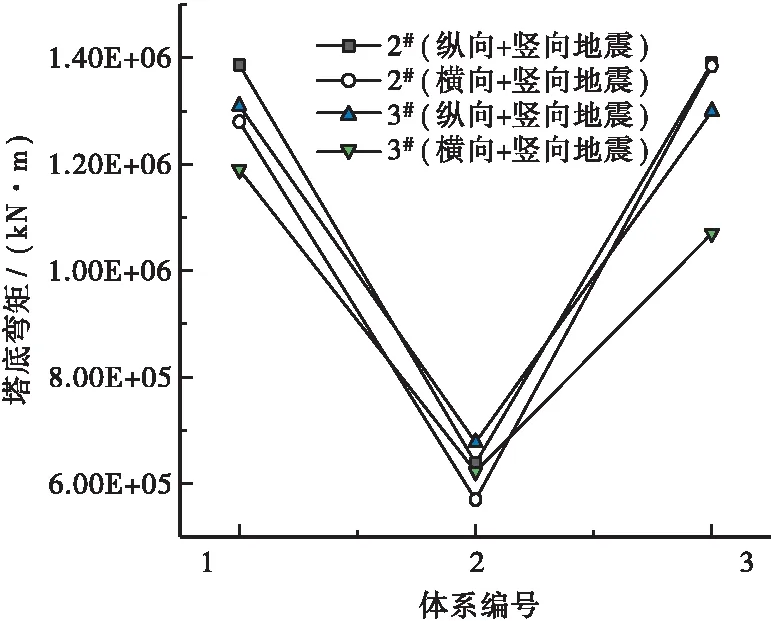
图10 塔底弯矩

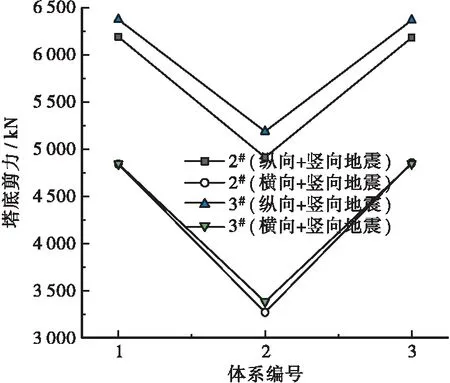
图11 塔底剪力

c.跨中挠度。

两种地震组合方式下的跨中挠度见图12。分析图12可知，体系1的跨中挠度最小，体系2的跨中挠度最大，但最大挠度与最小挠度相差不到20 cm，说明不同体系对跨中挠度影响不大。

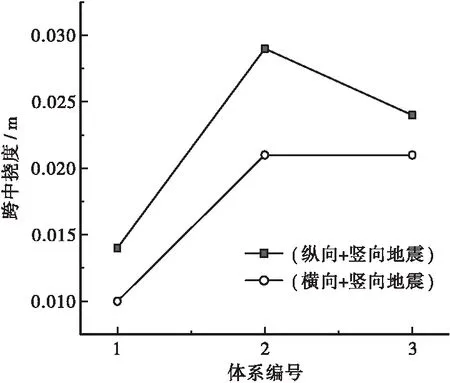
图12 跨中挠度

4.3 塔梁刚度变化

为探究合理的塔梁相对刚度，保持主梁刚度不变，将桥塔刚度在原桥刚度的0.5EI到1.5EI范围之间等梯度变化，变化梯度为0.1EI，分析各种不同的塔梁刚度组合下桥梁结构内力和变形的变化趋势。

a.塔顶位移。

塔顶位移在两种地震组合方式下随塔梁相对刚度的变化见图13和图14。分析图13可知，横向+竖向地震作用下2#和3#塔顶纵向位移均很小，不到1 mm，可忽略不计。纵向+竖向地震作用下2#和3#塔顶纵向位移接近0.01 m，也较小，可忽略不计，说明塔梁刚度对塔顶纵向位移影响不大。

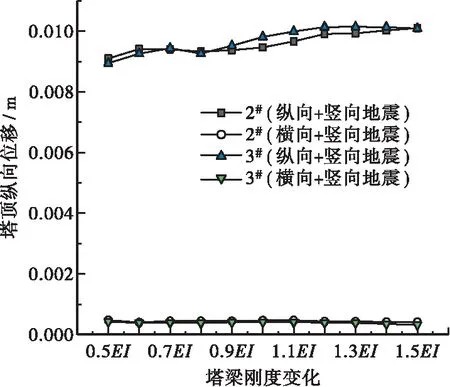
图13 塔顶纵向位移

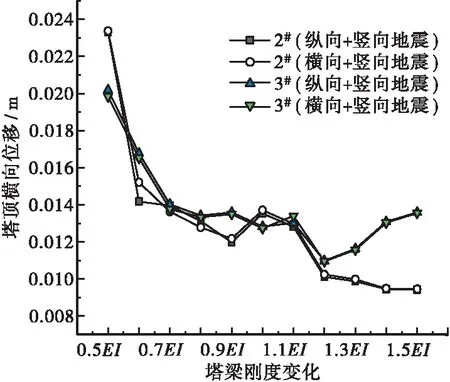
图14 塔顶横向位移

据图14分析可知，塔顶横向位移基本上随塔梁刚度增加而减小，2#和3#塔顶横向位移在两种地震组合方式下的变化规律相似，说明塔顶横向位移对地震动输入方式不敏感。

b.塔底内力。

2#和3#桥塔的塔底内力在地震作用下随塔梁刚度的变化规律见图15和图16。据图15分析可知，塔底内力基本上随塔梁刚度增加而线性增加。结合塔顶位移分析可知，当塔梁刚度在0.7EI至1.1EI范围内时的塔顶位移和塔底内力均较小，可作为工程需要的斜拉桥体系。

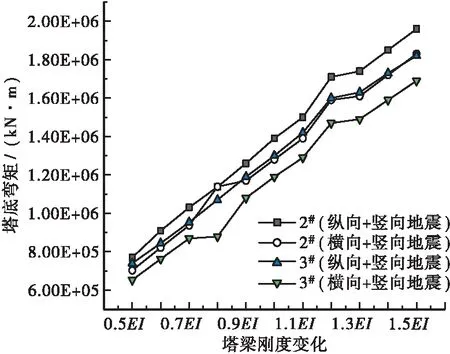
图15 塔底弯矩

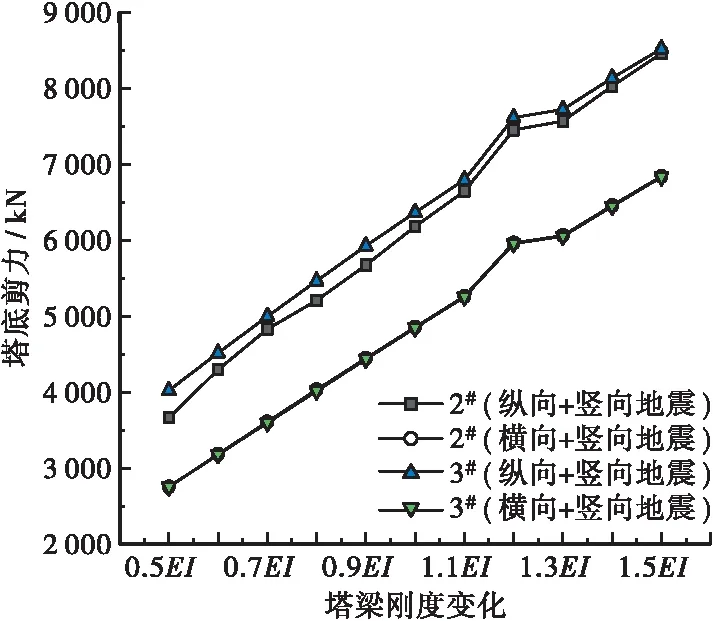
图16 塔底剪力

c.跨中挠度。

跨中挠度在地震作用下随塔梁刚度的变化趋势见图17。分析图17可知，跨中挠度和塔顶横向位移变化规律一致，皆随塔梁刚度的增加而减小。塔梁刚度在0.7EI至1.1EI时跨中挠度波动不大，可以作为工程需要的斜拉桥体系。

图17 跨中挠度

5 结论

本文进行了地震作用下斜拉桥刚度配置以及合理体系的研究，主要结论如下：

a.通过改变塔墩高度，探究了塔顶位移、塔底弯矩和跨中挠度的变化规律，以此确定最合适的塔墩高度，研究表明在地震作用下原体系的塔墩高度为最合适塔墩高度，此时塔顶位移和跨中挠度最小，而塔底内力也不大。

b.3种体系下位移响应相差不大，但体系2下的塔底内力最小，因此半漂浮体系为最合适体系。

c.塔梁刚度对塔顶位移影响不大，跨中挠度随塔梁刚度增加而减小，而塔底内力随塔梁刚度增加而增加。综合考虑，当塔梁刚度在0.7EI至1.1EI范围内的体系均可作为工程需要的体系。