基于MASTA的圆锥滚子轴承的低成本滚子母线设计

王修坤, 刘飞涛

（上海汽车集团股份有限公司 技术中心, 上海 201804）

1 前言

圆锥滚子轴承因能够承受轴向和径向的组合载荷、且预紧后轴系刚度好，被广泛应用于汽车变速箱承受重载的位置上。圆锥滚子轴承的滚子母线形状对于圆锥滚子轴承内部的应力分布及使用寿命具有重要影响。滚子母线是直线的圆锥滚子轴承在实际应用和理论分析中，已经被证明是不可取的，其受到载荷后滚子边缘和滚道之间有一个弹性趋近量，这个弹性趋近量使滚道靠近滚子端部的区域被拉伸，使滚子端部发生应力集中。滚子沿轴向的应力呈现哑铃形，即所谓的“边缘效应”[1-2]。“边缘效应”导致滚子端部接触应力飙升，而轴承的寿命和滚子接触应力的 7次方成反比[3]。“边缘效应”产生的高应力会使滚道边缘提前发生疲劳、剥落，剥落随后向滚道中央迅速扩展，使轴承发生早期失效，降低轴承的旋转精度和使用寿命，并引发整车 NVH 问题。

为克服滚子的“边缘效应”，将直线型母线修改为曲线型母线是根本思路，这是因为经过优化设计的曲线型滚子母线可以改善滚子和滚道之间的应力分布、避免发生应力集中。除此之外，曲线型滚子还能改善滚子和滚道的润滑条件，也能改善由于轴承安装、加工误差和轴系工作时挠曲而发生的滚子偏载问题。Lundberg[4]使用解析法建立了对数母线公式，基于此公式中的母线形状，滚子可以获得理论上均匀的矩形接触痕迹。P. M. Johns 和 R. Gohar[5]在 Lundberg 公式基础上增加了滚子接触痕迹的半长和半宽尺寸，建立了理论上更为合理的对数母线公式。日本 NTN 的Hiroki FUJIWARA[6]和 Tatsuo KAWASE 进一步优化出可以考虑滚子偏转的对数母线公式。

计算机技术的进展，使数值分析法优化设计滚子母线变得更加便捷。马家驹[7]基于影响系数法分析了直线型、圆弧型、圆弧-直线型、对数型和直线加对数型滚子修形曲线在均匀载荷下滚子的应力分布。夏新涛[8]等采用 ANSYS 软件分析了滚子凸度偏移对于滚子应力分析的影响。圆弧型和对数型母线都能很好地解决滚子的“边缘效应”问题。

现行的滚子凸度加工工艺主要有贯穿磨削法和贯穿超精法[9-10]，前者在普通无心磨床[11]上用特制砂轮和特制导轮，引导滚子以一曲线的轨迹通过磨削区，获得滚子修形曲线；后者主要通过双导辊引导和油石精研的方法获得修形曲线[12]，前者的机床成本和工艺难度都要低于后者。据滚子加工供应商的统计，加工高精度的对数型母线的机床成本是加工圆弧型母线机床成本的三倍以上。因此，从技术经济性的角度考虑，本文研究汽车变速器中圆锥滚子轴承的圆弧型和圆弧-直线型滚子的优化设计。

MASTA 是由英国 SMT 公司开发的一款基于the Microsoft.NET 架构建立的齿轴系统开发工具，可以完成齿轴系统的设计计算和分析。轴承滚子凸度设计和分析是 MASTA 的重要功能。MASTA 的操作界面友好，可以快速完成轴承滚子母线的设计，但尚未有文献介绍，本文基于 MASTA 10.2版本的计算分析功能，以某款手动变速箱中间轴上后端圆锥滚子轴承的滚子母线优化问题为例，用正交试验法优化出合理的滚子母线形状。

2 建模

2.1 基于 MASTA 建立变速箱计算分析模型

图 1 是以一款五速手动变速箱为例，使用MASTA 建立的变速箱计算分析模型。输入轴两端依靠球轴承支撑，中间轴两端依靠圆锥滚子轴承支撑，图 1 中框选的即为本次分析的圆锥滚子轴承，其标准代号为 30205，具体参数见表 1。

表1 轴承的结构参数

图1 使用MASTA建立的变速箱二维剖面图

为保证各个样本分析计算的一致性，本次计算中的轴承的预紧均为 0，且分析的工况都是轴承最大受力的工况。当滚子母线为直线时，受力最大的滚子在发动机满扭下的应力曲线如图 2 所示。由下图看出，除滚子两端区域外，滚子在轴向方向受力很不均匀，靠近滚子小端的应力大，靠近滚子大端的应力小，且呈线性递减。在滚子两端区域内，发生了严重的“边缘效应”， 最大边缘应力已经达到 4 000MPa，达到了滚子的应力极限。

图2 承受最大载荷的滚子沿轴向的应力分布

2.2 滚子的两种圆弧类修形

滚子的圆弧修形曲线分为两种，一种是将滚子母线修为圆弧形，即为纯圆弧修形；另一种是将滚子母线修为中间呈直线，两端是圆弧的修形方式，即为圆弧-直线修形。

2.2.1 纯圆弧滚子修形

令滚子母线中点为坐标原点，直线母线为 x轴，垂直于母线且过坐标原点的直线为 y 轴，那么第一种圆弧形的曲线公式如式（1）所示：

其中，R 表示圆弧修形的圆弧半径，a 表示圆心距离滚子中心截面的距离，图 3 是去除滚子两端倒角后，当圆弧半径为 2 000mm、a = 2mm时的修形母线。

图3 纯圆弧型滚子母线轮廓

2.2.2 圆弧-直线滚子修形

第二种修形方式是将滚子两端修形为圆弧，中间修形为直线，其修形曲线部分公式：

直线部分公式：

当滚子中直线段长度为 4，圆弧直径为 2 000mm 时的完整修形曲线如图 4 所示：

图4 圆弧-直线滚子母线轮廓

根据解析几何的相关知识，公式（1）、公式（2）和公式（3）可以统一为下面的公式：

3 分析

为便于分析，将17 粒滚子按照角度从小到大、逆时针的顺序排列，并将第 5 号滚子放在90°的位置上，如图 5 所示：

图5 轴承滚子的序号定义

当滚子无修形时，即滚子母线为直线时，各个滚子最大应力如图 6 曲线所示，当滚子母线为直线时，5 号滚子受到的应力最大、载荷最大，最大应力为 4 019.520 1MPa。

图6 各个滚子的最大应力

考虑到各个滚子的载荷和应力大小不同，因此本文将所有滚子中受力最大的滚子的应力作为评价滚子修形曲线优劣的标准。

3.1 纯圆弧型修形曲线的应力分析

根据公式（1）中展示的函数关系，影响滚子修形母线的因素只有圆弧半径 R 和母线中心偏移量 a，根据实际的常用工艺参数，将滚子修形母线圆弧半径和母线中心两个因素各取五个水平，分析的因素和水平如表 2 所示：

表2 影响纯圆弧滚子应力的因素和水平

根据现有两种因素、五种水平，可以建立如表 3 的全因子分析表格，运用直观分析的方法，可以发现偏心量对于滚子应力的影响更大：

表3 纯圆弧滚子应力的全因子水平试验分析表格

图 7、图 8 和图 9 是根据表中数据绘制的趋势图，根据趋势图和试验数据，可以判定偏心量是比圆弧半径更为重要的影响滚子应力的因素；最优的圆弧半径是1 000mm，最优的偏心量是1mm。

图7 圆弧半径对于纯圆弧滚子最大应力的影响机制

图8 偏心量对于纯圆弧滚子最大应力的影响机制

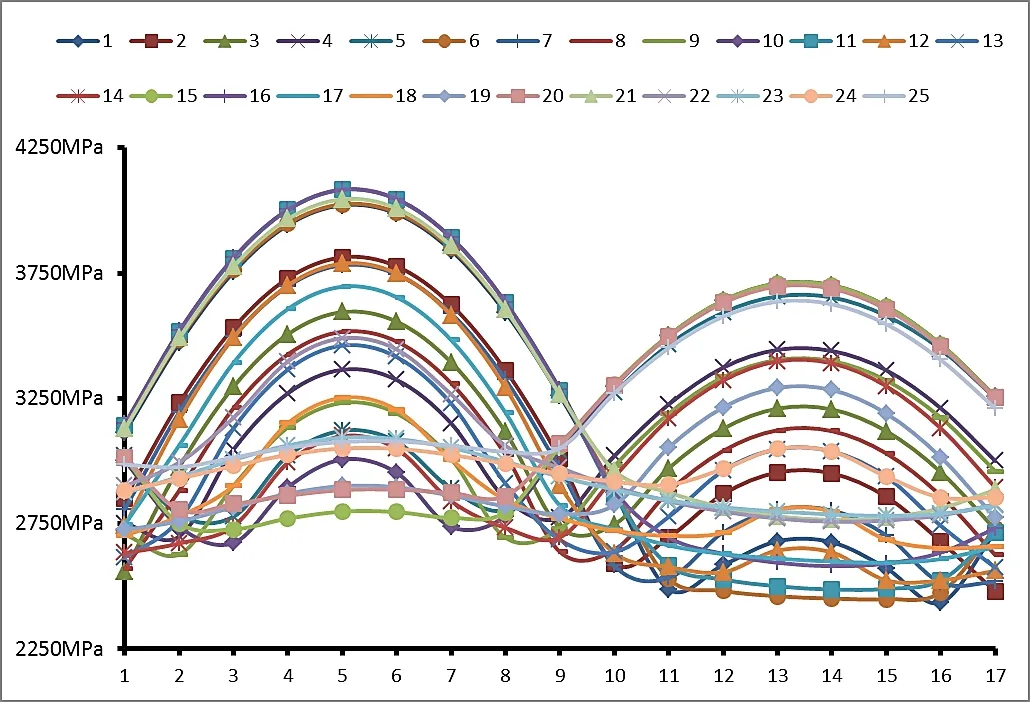
图9 表3中25种圆弧母线下各个滚子的最大应力

由图 7、图 8 和图 9 可以看出:

① 随着圆弧半径变小，轴承滚子的最大应力下降，且各个滚子的最大应力也趋于更加一致。当偏心量从 0 向 -2 变化时，轴承滚子的最大应力上升；但当偏心量从 1 向 +2 变化时，滚子应力先变小后升高；当偏心量为 +1 时，滚子应力最小。

② 就单个轴承受力而言，17 粒滚子受力呈现双峰值的特性，即第 5 粒滚子和第 13 粒滚子分别代表上下半圈滚子应力的峰值，滚子应力的优化主要是降低第 5 粒滚子和第 13 粒滚子的应力。

③ 从正交分析的结果可以看出，对于滚子应力大小影响的顺序为：圆弧半径＜圆弧偏心量。

3.2 圆弧-直线型修形曲线的应力分析

为保证所有影响应力变化的因素都能被考虑进凸度修形的优化工作中，同时分析的额数量又尽可能地减少，建立如表 4 的因子水平表格和表 5 的正交分析试验表格。

表4 影响圆弧-直线型滚子应力的因素和水平

表5 圆弧-直线的正交试验分析表格

根据表 5 中的数据分析，对于滚子应力影响最大的因素是偏心量，其次是滚子的修形半径，影响最小的是滚子修形中的直线长度。最优的水平组合是修形半径为1 000mm、偏心量为1mm、修形直线长度为 1mm。根据上表中数据建立的趋势分析图如下所示。

图11 偏心量对于圆弧-直线型滚子最大应力的影响机制

图12 直线长度对于圆弧-直线型滚子最大应力的影响机制

图13 各种圆弧-直线母线下各个滚子最大应力的情况

针对正交试验分析的影响，得出圆弧半径、偏心量和直线长度对于滚子接触应力的影响机制，从图 10 ～ 13 可以看出：

图10 圆弧半径对于圆弧-直线型滚子最大应力的影响机制

① 增加修形母线中的直线部分前后，圆弧半径和偏心量对于滚子应力的影响机制不发生变化。

② 就单个轴承受力而言， 17 粒滚子受力呈现双峰值的特性，即第 5 粒滚子和第 13 粒滚子分别代表上下半圈滚子应力的峰值，滚子应力的优化主要是降低第 5 粒滚子和第 13 粒滚子的应力。

③ 随着滚子修形圆弧半径的减小，轴承滚子的最大应力不断下降，且各个滚子的最大应力也趋于更加一致。从整个试验来说，随着修形圆弧半径的下降，滚子应力下降；当滚子圆弧中心向大端偏 1mm 时，滚子的应力最小，此时向滚子大端或小端偏斜时，应力迅速上升，因此偏心量的合理区间为 [0, 1.5]。

④ 从整体而言，直线段越短，越有利于降低滚子的接触应力，直线段长度对于轴承滚子应力的影响趋势和圆弧半径对于滚子应力的影响趋势刚好相反。

⑤ 从正交分析的结果可以看出，对于滚子应力大小影响的顺序为：圆弧半径＞圆弧偏心量＞直线长度，其中随着圆弧半径变大，应力变大，这是因为圆弧半径越大，修形量越小；随着偏心量向右移动，应力变小，因此在实际加工中，应使圆弧中心在 [0, 1] 的范围内浮动；直线段越长，应力变大，因此实际加工中，应尽量减少直线段的长度。

由上文可知，最优圆弧-直线组合是修形半径为 1 000mm、偏心量为 1mm、修形直线长度为 1mm，此时计算出的滚子最大应力是 3 052.06MPa，仍略大于纯圆弧的最优曲线下的最大应力 3 050.73MPa（基于修形半径为 1 000mm、偏心量为 1mm 的组合）。可见，纯圆弧的滚子母线要优于圆弧-直线的母线。

4 结束语

本文考虑到手动变速箱低成本的特性，将滚子圆弧修形作为改善滚子应力分布的优化目标，使用 MASTA 和正交试验法作为优化设计工具，找出最优化的圆弧：

① 应优先选择纯圆弧型滚子母线，应尽量降低滚子母线的修形圆弧半径，最好在 2 000mm以下，偏心量应尽量选择在 [0, 1.5] 的范围内。

② 如选择圆弧-直线型滚子母线，同样应尽量降低滚子母线的修形圆弧半径，最好在 2 000mm以下，偏心量应尽量也应选择在 [0, 1.5] 的范围内。对于直线段长度，应尽量减少，在 1mm以内为优。