基于效率优化的混合动力车辆强化学习能量管理策略研究*

杨宁康，韩立金，2，刘 辉，2，张 欣

（1.北京理工大学机械与车辆学院，北京 100081；2.北京理工大学前沿技术研究院，济南 250300；3.中国北方车辆研究所，北京 100072）

前言

效率作为机电复合传动系统车辆的重要研究内容，可用于传动系统的设计和能量管理策略的制定，建立一个通用的综合传动系统效率模型具有重要意义。Mashadi等［1］对THS的效率进行分析时，只涉及到了发动机和电机A、B的效率。Kim等［2］对一双段式机电复合传动车辆控制策略的研究建立在动力系统总效率的观点上，但在计算时假定经过机械部分无功率损失，仅考虑了电机损失。清华大学朱元等［3］假设所有机械传动效率都为100%且没有齿轮冲击等。北京理工大学阚振广等［4］建立和研究了某车辆综合传功装置直驶机械工况下的功率损失模型，但各部件功率损失模型较简单。以上已有的传动系统效率的研究各有缺陷，须建立普适且更加精确的效率模型。

作为混合动力车辆的重要研究领域，能量管理对于改善车辆性能、提升经济性及动力性有重要作用。根据已有的研究，众多能量管理方法大体划分为两类：基于规则和基于优化。基于规则的策略包括确定性规则［5］和模糊规则［6］。由于其方便实现的优点，基于规则的策略仍是目前工程实际中应用最广泛的方法；但较差的适应性和不涉及最优化的问题约束了其性能。基于优化的策略包括全局优化，如动态规划［7］、二次规划［8］、粒子群优化［9］和极小值原理［10］；实时优化，如等效燃油消耗［11］、模型预测控制［12］。对于全局优化，虽可得出理论上的最优结果，但繁重的计算负担和对工况完整知识的需求限制了其应用。对于实时优化，其局部优化的特性难以获得满意的结果，对实时性的高要求也为实际使用设置了阻碍。

目前，强化学习被逐渐引入到能量管理的研究，由于其良好的性能而得到迅速发展，并被视为未来的重要方向［13-14］。强化学习有两个主要优点：（1）由于良好训练的智能体根据奖励的长期积累做出决策，单步贪婪的策略实际上也是长期最优；（2）强化学习不需要建立精准的控制系统的模型，只须学习与系统交互产生的经验，从而避免了引入模型带来的偏差。

传统能量管理策略中仅以发动机燃油消耗作为经济性指标，将传动系统的效率取为定值，未考虑效率的动态特性，与真实车辆存在偏差。以综合效率作为目标能更加全面地反映行驶时的实际情况，从而提升能量管理策略的性能。但综合效率的计算涉及各个部件的模型，有众多的变量和复杂的方程，该缺陷限制了效率作为优化目标的应用。如采用传统方法制定策略，计算负担重，优化问题求解困难，因此引入强化学习作为优化方法。在强化学习中，智能体与对象的交互产生经验，通过学习经验，从中得出最优控制策略，从而避免了求解复杂方程的困难。

本文中分析各关键部件的效率建模方法，并在此基础上进一步完善效率影响因素，得到更加精确的效率模型。之后分析耦合机构的效率随电功率分流系数的变化情况，进而建立综合效率计算模型。然后以综合效率最优作为目标，提出基于强化学习的能量管理策略，并进行仿真验证。最后搭建试验台架，验证了所提出的效率模型和能量管理策略。

1 混联式混合动力系统方案

混联式系统如图1所示。该系统主要由发动机、电池组和传动系统3部分组成。传动系统包括功率耦合机构和前传动。其中功率耦合机构由2个行星排、2个永磁同步电机A、B和1个定轴齿轮副组成。该传动系统通过耦合机构可实现两种动力输出方式：EVT1模式（分速汇矩式）、EVT2模式（分速汇速式）。

图1 混联式系统

EVT1模式：离合器分离，制动器接合，主要用于车辆行驶速度较低、需求转矩较大时。

EVT2模式：离合器接合，制动器分离，主要用于车辆行驶速度较高、需求转矩较小时。

2 机电复合传动系统关键部件效率模型研究

2.1 定轴齿轮效率模型

定轴齿轮的功率传递效率通常都较高，所以在使用定轴齿轮效率时常采用经验值。为进一步提高计算精度，将采用理论计算的方法获得齿轮啮合效率。

目前定轴齿轮效率计算公式以苏联学者库德略夫公式和日本学者两角宗晴公式应用最为广泛。库氏公式精确性差，比较粗糙；两角宗晴公式忽略了摩擦力对驱动力矩的影响。基于上述两种方法，本文中考虑齿廓间摩擦力对驱动力矩的影响，采用更加精确的齿轮效率计算公式。在齿轮传动过程中，滚动摩擦损失很小，一般忽略不计，只考虑滑动摩擦损失对效率的影响。外啮合下齿轮效率的精确公式［15］为

式中：z1、z2为齿轮齿数；f为摩擦因数；α'为啮合角；kε1、kε2和kε为 与ε1、ε2有 关 的 系 数 ，其 中ε1=αa2为两齿轮的顶圆压力角，其计算方法由节点位置决定，如表1所示。

表1 kε1、kε2和kε的计算式

2.2 行星机构效率模型

对于行星机构的效率，啮合功率法使用较多，但须准确确定功率流的方向，在多行星排中使用极不方便，且难以保证精度。因此选择相对功率法计算行星机构效率，计算效率时假设如下：

（1）只计算和相对运动有关的齿轮啮合损失，与牵连运动有关的损失忽略不计；

（2）相对运动的齿轮啮合损失与定轴齿轮传动相同。

单行星排的效率损失等于它的相对功率Pr经一对外啮合和一对内啮合齿轮时的功率损失。若外啮合效率为ηe，内啮合效率为ηi，则相对运动效率ηr为

而相对功率Pr为

式中：Ts为太阳轮转矩；ns为太阳轮转速；nc为行星架转速。取P为行星排输入功率，则行星排效率ηc为

多行星排传动效率损失等于各排相对功率损失之和，其效率为

式中：η'r、η″r为各行星排的相对运动效率，决定于行星排的啮合次数和结构；β'、β″为各行星排的相对功率系数。

2.3 带排损失计算

多片湿式离合器在分离状态下可简化为图2所示的一对摩擦副。摩擦片与对偶钢片之间充满了冷却润滑油，摩擦片相对于对偶钢片以角速度ω旋转。忽略摩擦片上沟槽的影响，并假定对偶钢片被固定。

图2 分离状态下摩擦副几何模型

在润滑油流量一定的情况下，相对转速较低时，由于离心力较小，离合器摩擦片之间始终充满润滑油，因此带排转矩将随转速差的增大而不断增大。当相对转速升高时，离心力变大，润滑油由于受到更大的离心力而不再充满在整个摩擦片之间，即油膜半径发生了变化。所以此时须引入等效油膜半径进行计算，如图3所示。

图3 高速下油膜收缩模型

整个湿式多片离合器的带排转矩［16］为

式中：n为湿式离合器的摩擦副数；μ为冷却润滑油的动力黏度；ω为摩擦片相对于对偶钢片的角速度；ho为摩擦片与对偶钢片之间的分离间隙；Re为等效油膜半径；Ri为摩擦副内径。其中，等效油膜半径Re可由式（8）计算求得。

式中：ρ为冷却润滑油密度；Q0为冷却润滑油流量。

另外，须考虑润滑油黏度随温度的变化，参考Rost给出的基于50℃参考温度下的黏温特性方程［17］可得

式中：μ'为通过试验拟合出的计算系数；μ40为参考温度为40℃时的润滑油动力黏度；T为润滑油的实际工作温度。

综上，最终得到考虑温度因素后的湿式离合器带排功率损失数学模型为

2.4 动力电池组效率模型研究

本文中采用动力电池组的等效内阻模型进行效率特性分析。为简化模型，只考虑SOC与电池开路电压的关系及温度与电池内阻的关系。通过恒电流充放电试验，测量并记录电池内阻随温度的变化数据，并通过最小二乘法曲线拟合可得到电池内阻与温度的关系表达式。郭宏榆等［18］研究发现4阶多项式可较精确地反映一般锂电池单体放电内阻和温度之间的关系：

由试验结果，当锂电池SOC在0.1～0.9范围内且在特定温度T0下时，开路端电压U与SOC之间存在关系如图4所示。

图4 锂电池单体SOC与开路电压曲线

特定SOC所对应的开路电压可由实验数据插值得出。

分析电池等效电阻模型的充放电过程，可得锂电池充放电效率关于温度Tb、SOC和充放电功率Pele的关系式为

式中：ηdis为锂电池放电效率；ηcha为锂电池充电效率。

2.5 其他效率模型

除上述效率计算模型，发动机与电机的效率采用效率MAP图插值获得。轴承、密封、搅油和风阻损失所占的比例很小，可忽略不计。

3 机电复合传动系统效率影响规律研究

3.1 耦合机构效率变化规律

耦合机构作为混联传动系统中重要的组成部分，其效率的变化对整个传动系统有重大影响，在考虑整个传动系统前，必须先研究耦合机构的效率。

耦合机构由行星机构和两电机组成，在进行功率传递时，一部分功率经行星机构组成的机械路传递，另一部分经两电机组成的电路传递，当两条路线传递的功率不同时，最终的耦合机构效率也不同，所以研究其功率分流特性对耦合效率的计算和优化有重要意义。

首先，要得到不同拓扑结构下电功率分流系数的数学模型。按图5所示，过程如下：

图5 复合传动系统结构图

令βele=为电池功率比例系数，Pi为耦合机构输入功率，Pele为电池组输出功率；当Pele＞0时，电池组放电；Pele＜0时，电池组充电。同时取βA=为电机A功率分流系数，I=为速比。

EVT1模式下，功率流传递形式如图6所示。

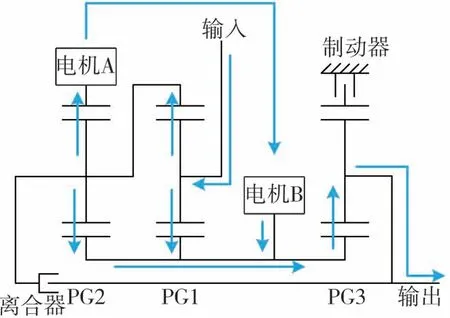
图6 EVT1模式耦合机构功率流（分速汇矩式）

结合功率平衡方程：

式中：PA为电机A功率；PB为电机B功率；ηA为电机A效率；ηB为电机B效率。可得出耦合机构效率ηcoup的计算式为

式中ηM'为双行星机构效率。

其变化规律如图7所示。

图7 EVT1模式耦合机构效率变化规律

从图7中可以看出，耦合机构效率ηcoup关于电机A的功率分流系数βA呈明显的非线性关系，且效率随功率分流系数先增大后减小。当电机功率分流系数在零附近时，效率较高。同时，ηcoup还与电池功率比例系数βele有关，当βele=0、βA=0时，系统不存在电功率流的传递，此时耦合机构效率最高，为机械传动效率。

EVT2模式下，功率流传递形式如图8所示。

图8 EVT2模式耦合机构功率流（分速汇速式）

结合功率平衡方程，ηcoup的计算式为

其变化规律如图9所示。

图9 EVT2模式耦合机构效率变化规律

显然，与EVT1模式相比，EVT2模式下耦合机构效率ηcoup关于电机功率分流系数βA呈复杂的非线性关系。因每个电机功率分流系数对应两个行星机构效率，所以，耦合机构效率在每个电池功率比例系数下也对应两个效率值。且ηcoup关于βA呈先增后减的趋势。当两电机功率分流系数在零附近时，耦合机构效率能维持在高效区。

3.2 综合效率模型

在耦合机构效率的基础上，考虑到发动机、电池组、前传动和主减速器的功率损失可得系统综合功率传递效率ηz表达式为

式中：Pi、Po为耦合机构输入、输出效率；ηe发动机效率；ηF为前传动效率；ηT为减速器效率。

4 基于效率优化的能量管理

4.1 能量管理策略的制定

在完成耦合机构效率变化规律的研究和系统综合效率模型的建立后，以综合效率最优为目标，进行能量管理策略的制定。

作为最基本的强化学习算法，Q学习因其有效性与简洁性而被广泛使用。在本文中，状态变量S为

式中Pdem为需求功率，kW。

控制变量A为

式中：ne为发动机转速，r/min；Te为发动机转矩，N·m。

奖励函数为

式中：ηz为系统综合效率；λ＜0，ΔSOC=SOCSOCpre，用于限制电池组SOC的变化范围。

Rt取为在单个时间步长t的奖励，为估计长期收益，用回报Gt来表示t时刻后奖励Rt的累计值，其递推形式为

式中γ∈(0，1)为折扣因子。

策略b是从状态到选择每个动作的可能性的映射。将状态值值函数vb(s)定义为从状态s开始并且遵循策略b的期望回报，表示为

式中St为t时刻的状态。

同时，动作值函数qb(s，a)也定义为从状态s开始、采取动作a并且遵循策略b的期望回报：

式中At为t时刻的动作。

之后，其递推形式也可以得出：

式中：st、st+1表示t及t+1时刻的某一特定状态；at、at+1表示t及t+1时刻的某一特定动作。

将最优动作值函数q*(s，a)定义为在所有策略中的最大动作值函数，其递推形式可以表述为

如果q*(s，a)已知，则最优策略b*可通过最大化q*(s，a)来获得。

由于最优动作值函数的真实值难以获得，采用q*(St，At)的估计值——Q(St，At)来代替。在包括Q学习的时序差分方法中，估计值Q(St，At)与更优估计值Rt+γQ(St+1，At+1)之间的差值用于更新Q(St，At)：

式中α为学习率。

在Q学习算法中，At+1按下式选择：

因此，Q学习算法中Q(St，At)的更新公式［19］为

表2展示了Q学习算法的伪代码，其中的一幕即为一个完整的循环工况。在多次尝试比较性能后，学习率α与折扣因子γ分别取为0.9与0.95。控制步长为1 s。

表2 Q学习算法伪代码

策略b是关于Q的ε-贪婪，如式（29）所示：

4.2 仿真结果

为证明所提出的能量管理策略的有效性，将其与基于规则的策略进行对比，并采用图10所示的标准UDDS工况进行验证。

图10 测试工况

随着工况的运行，每次更新时Q值的改变量也逐渐减小。图11为每个完整工况下Q值的平均差异的变化。当平均差异小于1时，认为算法收敛，则在108次循环后，策略学习结束。

图11 Q值的平均差异

图12为两种策略下SOC的变化轨迹，初始SOC为0.6。相比于基于规则的方法，所提出的策略不仅波动较小，而且能更好地维持结束时的SOC。图13展示了整个工况中发动机与电池组之间的功率分配。可以看出，基于学习的策略中，发动机功率更加平稳、波动更小。

图12 SOC轨迹

图13 功率分配

图14为两种策略下的发动机工作点。显然，相比于基于规则的方法，基于学习的策略中的工作点不仅更加集中，而且更多地位于低燃油消耗区中，从而实现更合理的分布。

表3为两种策略的仿真结果，其中综合效率是以传动系统输出的总能量除以柴油完全燃烧所释放的能量计算而出。基于学习的策略相对于基于规则只消耗91.42%油耗，而综合效率有较大提高。显然，本文中提出的能量管理策略在实现较好的燃油经济性的同时也能维持电池组的SOC。

表3 仿真结果

5 试验验证

为验证耦合机构效率模型的正确性和所提出能量管理策略的有效性，搭建机电复合传动试验台，其示意图如图15所示。由一台涡轮增压柴油发动机、两台永磁同步电机、一组动力电池组、电涡流测功机、惯量组、耦合机构传动箱和相应的控制系统和数据采集系统等组成。

图15 机电复合传动系统试验台架示意图

机电复合传动系统试验台架实物图如图16所示，系统动力由涡轮增压柴油发动机和两个永磁同步电机通过耦合机构输出，测功机用于模拟路面负载。耦合机构传动轴上装有转速转矩传感器，用于实时测量传动系统的转速转矩信息。动力电池与电机控制器之间装有直流电流传感器，用于实时测量电池充放电电流，从而估计电池SOC的变化状态。其主要设备基本参数如表4所示。

表4 机电复合传动台架设备参数

图16 机电复合传动系统试验台架

首先进行耦合效率模型的试验验证。在EVT2模式下，根据发动机正常工作下的转矩范围，设定加速踏板行程分别为30%、35%、40%、45%、50%和55%，同时功率耦合机构输出端加载To=180 N⋅m的负荷。各部件的输出特性如图17所示。

图17 各部件输出特性试验结果

在得到以上试验数据之后，可计算出耦合机构的试验效率，结果如图18所示。

图18 耦合机构试验效率曲线

根据上文所提出的耦合效率计算模型式（15），可计算出耦合机构效率的理论值，进而计算出理论值与试验值的差值。同时将传统效率计算方法作为对比，将定轴齿轮的效率取为定值0.98，采用普通的啮合功率发计算行星机构的效率，并且采用经验插值计算带排损失，其结果如图19所示。

图19 耦合机构效率误差变化曲线

由图19可以看出，基于本文提出方法的耦合机构计算效率与试验效率两者误差主要控制在0.015以内，而传统的效率计算方法的误差普遍在0.03以上。由表5可知，在采用新的效率计算方法后，效率的平均绝对误差由0.038 9下降到0.010 1，而最大绝对误差由0.052 2下降到0.017 9。证明了耦合机构效率数学模型的准确性和有效性。

表5 效率计算误差

表6展示了所提出的能量管理策略仿真与试验结果的偏差。各部件仿真模型精度与试验台架中实际特性存在差距，导致燃油经济性的实际值与仿真值存在差异。在初始值相同的情况下，最终SOC接近，燃油消耗的偏差维持在10.04%，证明了所提出的能量管理策略的有效性。

表6 燃油消耗试验结果

6 结论

本文中以一辆混联式机电复合传动车辆为研究对象，提出新的效率模型和基于效率最优的能量管理策略。

（1）建立了混联式混合动力系统各个关键部件精确的效率模型。

（2）分析了电功率分流系数对耦合机构效率的影响规律，并建立了综合效率的计算模型。

（3）提出了以系统效率最优为目标，基于强化学习的能量管理策略，并进行仿真。结果表明，相比于基于规则的方法，能大幅度改善燃油经济性并更好地维持SOC的稳定。

（4）搭建了试验台架，验证了所提出了效率计算模型的正确性以及能量管理策略的有效性。