基于蚁狮-差分进化算法的可借贷灵活期限项目组合选择模型

伍健栋，刘勇军

（华南理工大学工商管理学院，广州 510640）

随着市场经济的不断发展，企业间竞争日益加剧，如何在众多与企业经营发展密切相关的项目中选择合适的项目进行投资，进而加强企业自身的盈利能力、抗风险能力以及竞争力等已成为企业最关注的问题.而项目组合选择研究的正是如何在一组有限的可选项目中挑选若干合适的项目，进而在满足资源限制等约束的前提下，最大限度地实现组织目标的问题［1］.

作为投资组合领域的一个重要分支，项目组合选择问题可追溯至Markowitz于1952年提出的均值-方差模型［2］.之后，一些学者结合项目管理背景，展开了对该问题的研究.Ghasemzadeh等［3］提出了项目组合选择的0～1整数规划模型.Carazo等［4］引入多目标规划模型解决项目选择与调度问题.Beşikci等［5］研究了资源紧缩政策下的多项目环境问题.Kalashnikov等［6］将精益六西格玛项目组合表示为一个双目标二次规划问题并求解.Liesiö等［7］利用偏好规划构建鲁棒项目组合优化模型.王勇胜等［8］建立了不确定多期滚动项目组合选择模型.陶莎等［9］考虑了项目间交互作用及参数不确定性，提出项目组合选择鲁棒优化模型.Song等［10］基于可接受性分析方法解决了多准则项目组合问题.李星梅等［11］将鲁棒优化理论拓展到主动打断项目组合选择问题中.闫庆友等［12］构建了动态主动打断项目组合选择模型.

已有研究大多只考虑了在固定期限内进行项目的选择与调度.但由于组织目标及资源限制等多种因素的影响，投资者很难事先主观设定合适的期限进行投资；若设定不当，则会影响组织目标的实现.因此，Jafarzadeh等［13］提出了基于所选项目执行期来确定投资期限的项目组合选择整数规划模型.随后，Liu和Zhang［14］提出了考虑消费因素与破产风险控制的灵活时间期限项目组合选择模型.然而，这两个模型都是在不可借贷的假设下建立的，而现实中投资者通常是允许借贷的.因此，本文考虑了资金的可借贷因素，在借贷利率不一致且存在借款限额的情况下，提出了具有灵活时间期限的项目组合选择模型.针对所提出的非线性规划模型，设计了蚁狮-差分进化算法进行模型求解.最后，结合数值算例与模型对比分析阐明了模型和算法的有效性，并通过参数灵敏度分析探讨了借款限额对投资决策的影响.

1 项目组合选择模型的构建

记αt表示在时刻t因项目组合提前完工获得的奖励或超期完工遭受的罚金；当t0，当t>T时，αt<0，否则αt=0.则项目组合因期限调整产生的奖惩额ΔWe为

记rB,t和rL,t分别表示时刻t的借入与贷出利率；Wt表示投资者在时刻t进行项目投资支出并收回完工项目收益后的资金净额；Bt表示时刻t的借款限额.那么，在完成投资前的任意时刻t，投资者若按最大限额借入资金Bt，其资金总额不得为负值，即Wt+Bt≥0.则当时刻t=1时，W1为投资者初始财富扣除此时产生的项目投资支出，得到

而当t=2,…,T*-1时，若此时资金不足(Wt<0)，则借入资金|Wt|，并在时刻t+1支付利息rB,t|Wt|；若此时仍有资金剩余(Wt>0)，则全部贷出，在时刻t+1获取利息收入rL,t Wt，即

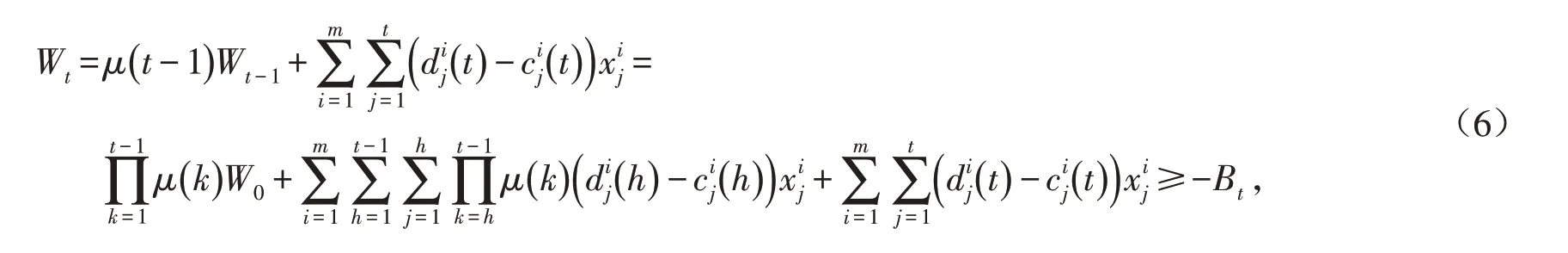
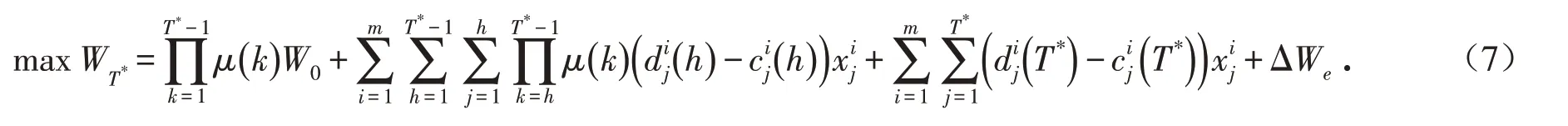
因此，本文通过进行最优项目组合选择与调度，在允许范围内决定实际投资期限，并在满足最大借款限制等约束的情况下，实现投资者最终财富的最大化，得到模型P如下：

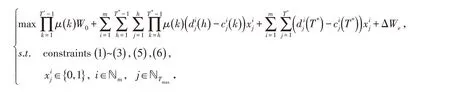
2 蚁狮-差分优化算法

2.1 蚁狮优化算法基本原理

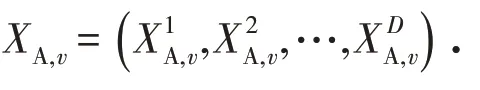
1）蚂蚁随机游走.每只蚂蚁为寻找食物在所有维度进行随机游走，随机游走的公式如下：

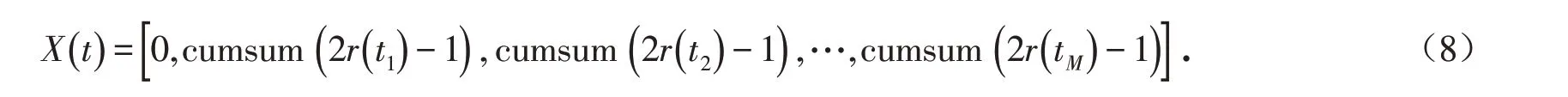
式中：t为蚂蚁游走的步数；cumsum为游走位置的累积值；M是算法最大迭代次数；r(t)为0或1的随机数.为确保蚂蚁在解空间内进行游走，需对游走位置进行归一化处理：

2）蚂蚁误入陷阱.蚁狮的位置可视为陷阱中心.每只蚂蚁基于蚁狮的适应度值，通过轮盘赌方式选择所误入的蚁狮陷阱，因此蚂蚁随机游走的范围边界受到蚁狮位置的影响：

式中：Rs(t)是蚂蚁围绕轮盘赌选择的蚁狮的随机游走；Relite(t)则是围绕精英蚁狮的随机游走.

3）蚂蚁滑落穴底.蚁狮刨出沙土迫使蚂蚁下滑，表现为陷阱边界随着迭代次数增加而减小：

其中：当t≤0.1M时，I=1；否则I=10w t M（w=2，t>0.1M；w=3，t>0.5M；w=4，t>0.75M；w=5，t>0.9M；w=6，t>0.95M），M为最大迭代次数.

4）蚁狮重筑陷阱.将蚂蚁与蚁狮按适应度排序，挑选适应度最优的N个位置更新蚁狮位置.

2.2 蚁狮-差分优化算法设计

基本ALO算法在求解复杂优化问题时仍存在早熟收敛和易陷入局部最优的问题，因此一些学者在其基础上开展了改进工作，如吴伟民等［19］提出了包含双重反馈机制的ALO算法，Dong等［20］在ALO算法中引入了动态随机游走方法和动态反向学习策略等.本文针对所提出的离散型非线性规划模型，通过采用适当的编码和约束处理方法，改进ALO算法部分环节，并引入差分进化算子等，从而设计了蚁狮-差分进化（Antlion Differential Evolution，ALDE）算法.

2）边界收缩限制.通过离散化连续变量来求解离散优化问题时，若连续变量变化幅度很小，离散化后的离散变量很可能未发生变化，因此蚁狮捕食范围在迭代后期的过度收缩会加剧算法难以跳出局部最优的问题.因此，本文对陷阱上界即式（13）进行改进如下：

式中：κd表示第d维变量离散化后可能取到的整数个数，继而限制了陷阱上界的收缩范围.

3）精英化的线性递增处理.为了提高算法前期的全局搜索能力，缓解算法早熟收敛的问题，将式（12）的精英化处理改为线性递增形式，降低个体前期受局部最优解的影响程度，如下：

式中：λ(t)=λmin+(λmax-λmin)⋅t M，λmin和λmax分别取0和0.5.

4）差分进化算子.差分进化算子的变异与交叉操作常用于改进算法全局搜索能力，如下：

式中：Uv为第v只蚁狮变异后的位置，a，b和c为随机选择的互不相同的蚁狮序号，F是[0.2,0.8]内的随机数，PCR控制交叉概率，θ为[0,1]内随机数，d0为{1 ,2,…,D}内随机数.记适应度函数为Fit(⋅)，当进化后的个体适应度更优，则替换原来的个体，即

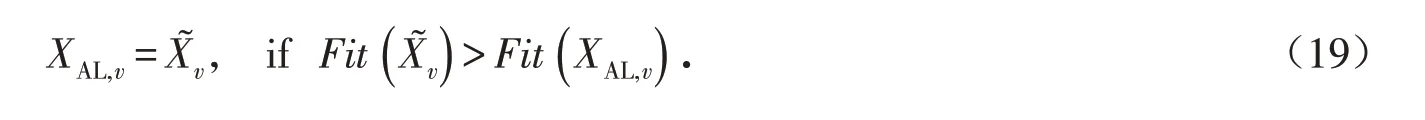
5）约束处理方法.本文采用自适应惩罚函数法［21］进行约束处理.记约束优化问题的目标函数为f(X)，第j个约束条件为gj(X)≤0，则解X的违反约束程度V(X)=∑j=1max(gj(X),0).记当前的最优适应度和最大违约程度分别为Fitg和Vg，则X的适应度值为

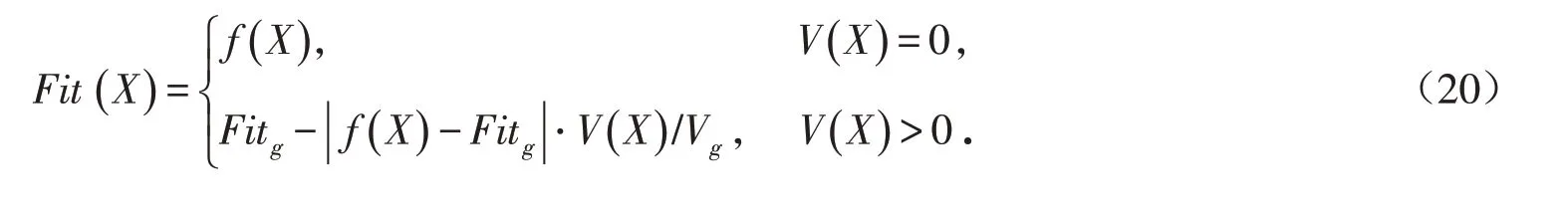
6）算法步骤.

Step 1：设置算法参数，随机生成初始的蚂蚁和蚁狮种群，计算相应的适应度值，记录初始的最优适应度和最大违反约束程度，令t=1.

Step 2：采用轮盘赌方式选择蚁狮，利用式（14），（15），（10）和（11）计算陷阱边界，利用式（8），（9）和（16）计算蚂蚁在陷阱中随机游走后的位置，计算适应度值.

Step 3：在所有蚂蚁和蚁狮中挑选适应度最优的N个位置对所有蚁狮位置进行更新.

Step 4：执行差分进化算子并更新蚁狮位置，更新最优适应度和最大违反约束程度.

Step 5：将精英蚁狮位置更新为当前适应度最优的蚁狮位置.

Step 6：令t=t+1，若t>M，则算法求解结束，否则返回Step 2.

3 算例分析

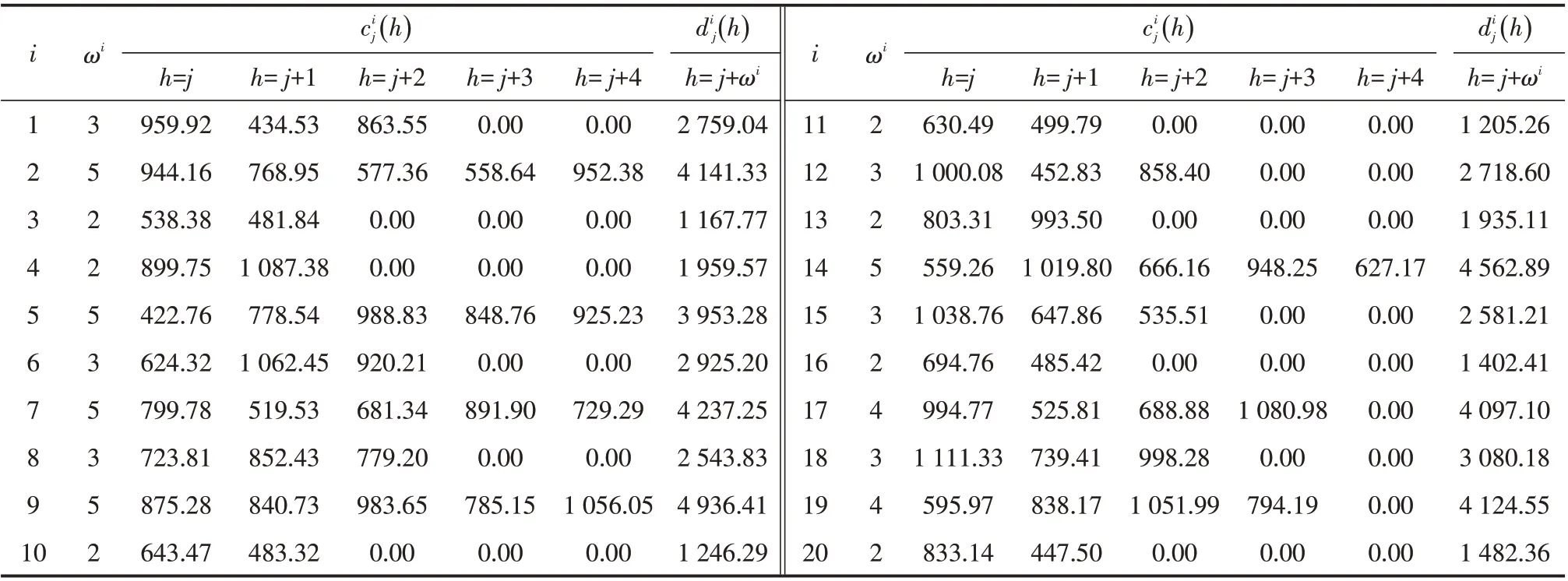
表1 可选项目的投资期数、投资支出与收益数据Tab.1 Implementation periods，expenditures and returns of the alternative projects

表2 期限调整奖惩值Tab.2 The amount of gain or loss due to adjusting the time horizon

为了说明ALDE算法的有效性，对基本ALO算法进行了对比测试，两者均运行100次.结果显示，ALDE算法求得的目标值的平均值、最大值、最小值和标准差分别为7 581.90、7 652.22、7 324.66和48.11，而ALO算法求得的对应结果则分别为7 004.42、7 436.36、6 506.13和203.85.图1展示了两个算法分别求得最大目标值的一次运算的迭代曲线.由此可见，ALDE算法的全局搜索能力更强，其求解效果及求解稳定性都明显优于ALO算法.

图1 ALDE和ALO算法的迭代曲线Fig.1 Iteration curves of algorithms ALDE and ALO

此外，为了阐明灵活时间期限及资金借贷因素对模型结果的影响，本文还与模型P在固定期限下的变体模型Pfixed以及不考虑资金借贷的灵活期限项目选择模型FTPP［13］进行了对比分析.表3展示了三个模型的求解结果，其中，各项目所对应数值j表示该项目开始投资的时间，若对应“－”则表示不投资该项目，WT*为完成投资时的最终财富值.如表3所示，本文模型P共选择了16个项目，如项目1、17和20在时刻1开始投资，项目19在时刻3开始投资等；实际投资期限T*=14，共逾期了4期完成投资，因此产生逾期罚金ΔWe=-925，最终财富WT*=7 652.22.而在固定期限下，由于前期资金不足及不能延期投资，模型Pfixed只能投资11个项目，其最终财富比模型P低了586.62，可见灵活时间期限决策赋予企业获取更高收益的机会.而不允许借贷的FTPP模型的实际投资期限T*=15，比模型P多推迟了一期，但最终只投资了13个项目，说明当不可借贷时企业在该期限内仍面临资金不足的问题，不能投资所有优质项目，最终财富值也比本文模型P低了930.17.

表3 不同模型下的投资策略及投资结果Tab.3 The investment strategies and results under different models

图2 借款限额取不同值时投资者的财富曲线及最终财富值Fig.2 Investor’s wealth curves and final wealth values with different upper bounds of borrowing amounts

4 结语

本文考虑了资金的可借贷性，在借贷利率不同且存在借款限额的情况下，提出了具有灵活时间期限的项目组合选择模型.然后，设计了蚁狮-差分进化算法来求解该模型，取得较好的求解效果.最后，通过算例分析，得出灵活时间期限决策以及允许资金借贷均有利于提高项目组合收益的结论.而参数灵敏度分析结果也表明，更高的借款限额使投资者有机会在更短期限内完成更多项目的投资，从而获取更高的回报.鉴于灵活时间期限决策的优越性，未来可考虑构建多类资产的灵活时间期限混合投资组合模型，探讨灵活时间期限对混合资产组合决策的影响.