基于张量网络的多脑运动想象脑电信号分类

傅倩婧，孔万增

(杭州电子科技大学计算机学院，浙江 杭州 310018)

0 引 言

脑机接口(Brain Computer Interface, BCI)是人脑与外部设备之间的接口，无需依赖动作，通过大脑来控制外部设备[1]。稳态视觉诱发电位和运动想象(Motor Imagery, MI)是最常见的脑机接口范式。运动想象脑机接口(MI-BCI)不仅可以给健康人提供更丰富的娱乐方式，还可以帮助有运动障碍的人恢复运动功能[2-4]。然而，MI-BCI系统存在识别率低、稳定性差等问题。为此，Nijholt等[5]采用多脑BCI技术进行脑机接口的研究，证实了其在脑机接口应用中的可行性。多脑BCI来源于超扫描思想，超扫描技术可以同时测量2个及以上被试的脑电信号[6-7]。相关研究表明，当多个被试处于同一环境进行交流时，大脑会产生同步共振现象[8-9]。传统方法处理脑电数据时，一般转换成向量的形式，这样会打乱数据的内部结构从而影响实验结果[10]。张量表示方法与神经网络之间有着紧密联系，可以把神经网络的数据转换成张量的形式。Novikov等[11]采用张量分解进行图像数据集的分类，取得了较好的分类效果。Yang等[12]在大规模视频数据集的分类任务中，使用张量链分解压缩门控循环单元(Gated Recurrent Unit，GRU)，结果表明张量链模型不仅可以减少参数数量，而且提高了分类性能。Wang等[13]采用张量环方法来压缩深度神经网络的全连接层和卷积层，减少了网络中的参数数量。虽然张量表示方法在处理大规模图片数据取得了一些成效，但是上述方法只学习了隐藏空间中的动态关系。本文针对高维数据输入问题，采用张量网络方法[14]来实现多脑运动想象脑电数据的分类，在输入空间中进行高维数据处理与模型参数压缩，以提高张量网络的性能。

1 多脑脑电数据采集

1.1 采集设备与被试

实验招募10名18～25岁的健康被试，随机分成5组，每组的2名被试，分别命名为“S1”和“S2”。通过2个相连的62通道Neuroscan放大器同步采集多脑脑电数据，2名被试同时进行相关任务。多脑脑电数据同步采集装置如图1所示。

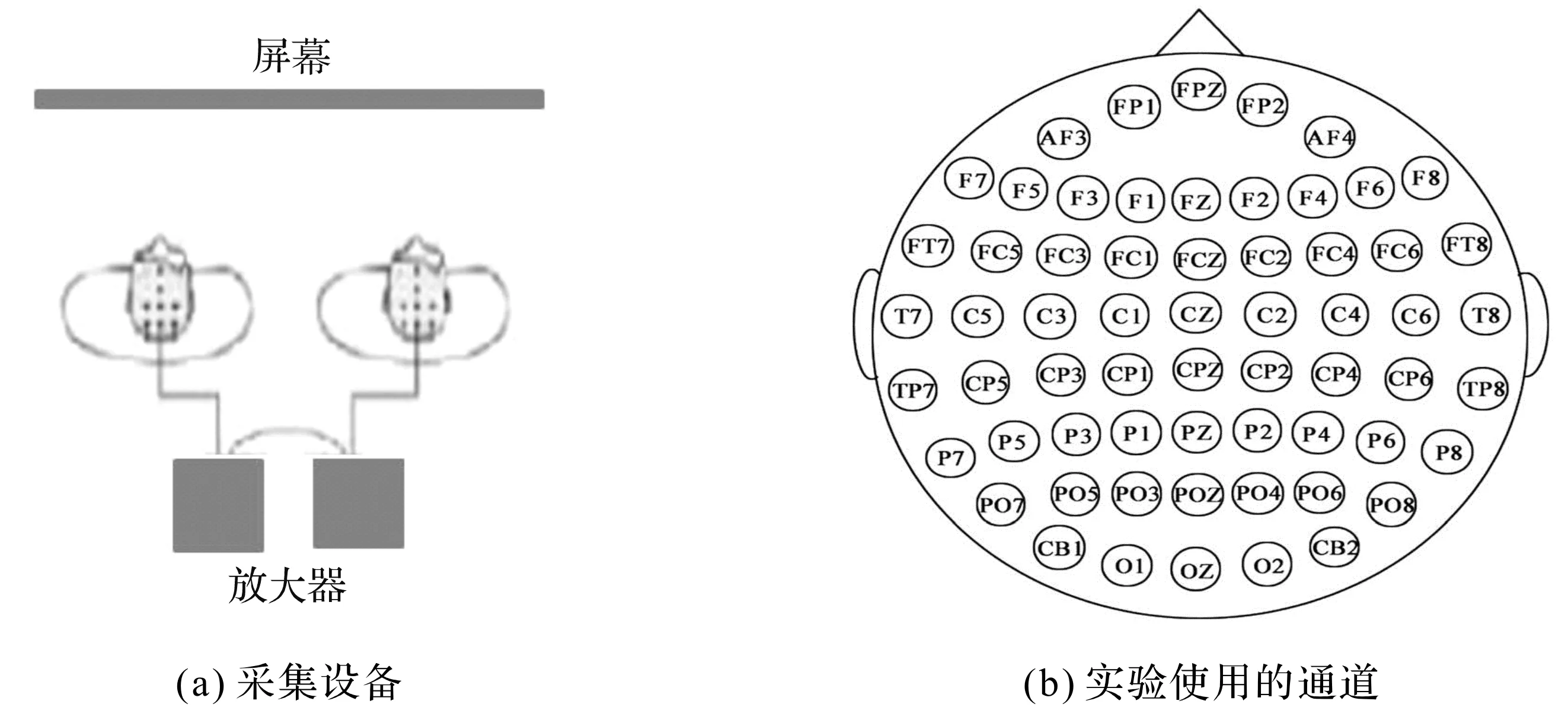
图1 多脑脑电数据同步采集装置

1.2 实验流程

实验包含4个阶段，其中1个是测试阶段。每个阶段包含125个实验，总共有375个实验。每个被试共有1 875个样本数据，单个样本大小为62×250。实验流程如图2所示。每个实验包括1.0 s的视频诱发，该阶段随机呈现3种状态(左手、右手、空闲)的视频。被试根据屏幕上呈现的任务提示，进行5.5 s大脑运动想象任务或空闲任务状态。由于实验过程比较漫长，随后进入2.0 s休息状态。

图2 实验流程

1.3 数据获取与预处理

原始脑电信号包含噪声数据，需要进行预处理以去除干扰成分。脑电数据中最主要的伪迹是眼电，借助EEGLAB工具包删除眼电干扰成分，脑电信号进行0.5～45.0 Hz的带通滤波。为了降低不同被试之间差异产生的影响，采用z-score函数进行数据归一化操作。采集得到5组脑电数据，对每组的2名被试沿着脑电数据通道维度进行拼接融合[15]。随机划分数据，80%作为训练集，20%作为测试集，训练集中选取10%作为验证集，用于张量网络模型训练过程中最佳参数值的确定。

2 实验方法

本文提出一种基于张量网络的多脑运动想象数据识别方法，通过共空间模式(Common Spatial Patterns，CSP)提取多脑运动想象脑电数据的空间分布特征，张量网络将提取的空间分布特征转化成张量的形式，输入张量网络进行多脑运动想象数据识别任务，使用张量分解方法来压缩网络的参数数量以解决张量网络中参数众多的缺点。多脑运动想象脑电数据分类方法如图3所示。

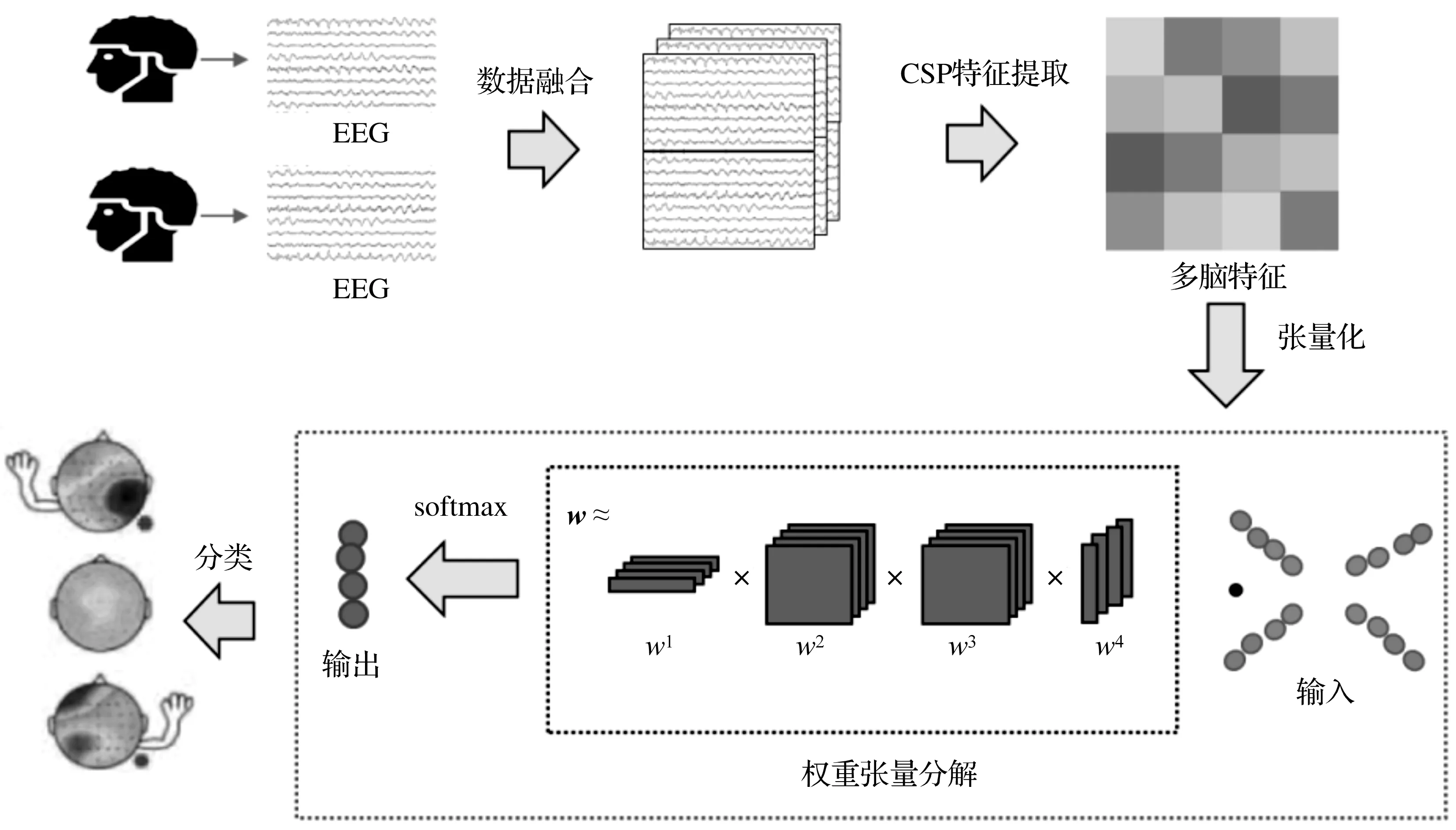
图3 多脑运动想象脑电数据分类方法

2.1 脑电特征提取

CSP广泛用于运动想象脑电数据的特征提取[16]，同时对角化两类任务的协方差矩阵，从多通道的脑电数据中提取出每一类样本的空间分布特征[17]。空间协方差矩阵表示如下：

(1)

式中，Z表示样本数据，trace函数表示矩阵对角元素之和。CSP算法目的是找到一组最优空间滤波器进行投影，使得2类信号的方差值差异最大，从而得到具有较高区分度的特征向量。由于多脑运动想象数据有3种状态信息，分别为左手、右手、空闲，因此，本文设计了一种针对三分类任务的CSP特征提取方法。实验中，针对3种状态，选取其中2个类别合成1类，并和剩下的1类进行计算投影矩阵。

2.2 权重张量分解

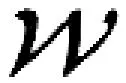
张量分解是低秩近似表示高阶数组的一种方法。目前流行的张量分解方法包括Canonical Polyadic(CP)分解[18]、Tucker分解[19]和Tensor Train(TT)分解[20]。

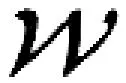
(2)

式中，∀r∈[1,…,R],g1,r∈Rm1，g2,r∈Rm2，g3,r∈Rm3，R∈Z+是CP分解对应的秩一张量的数量，称为CP-rank。“⊗”表示克罗内克积。权重张量的CP分解如图4所示。

图4 权重张量的CP分解

Tucker分解就是通过1个N阶张量∈RR1×R2×…×RN和N个因子矩阵B(n)∈RIn×Rn(n=1,2,…,N)相乘得到原始张量。Tucker积在所有模上进行乘法运算，3阶权重张量∈RR1×R2×R3可写为：

(3)

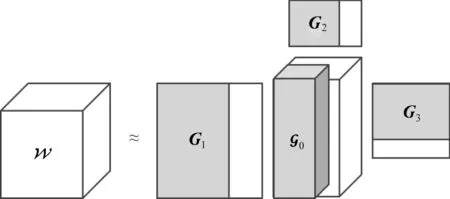
图5 权重张量的Tucker分解

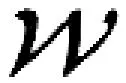
(4)

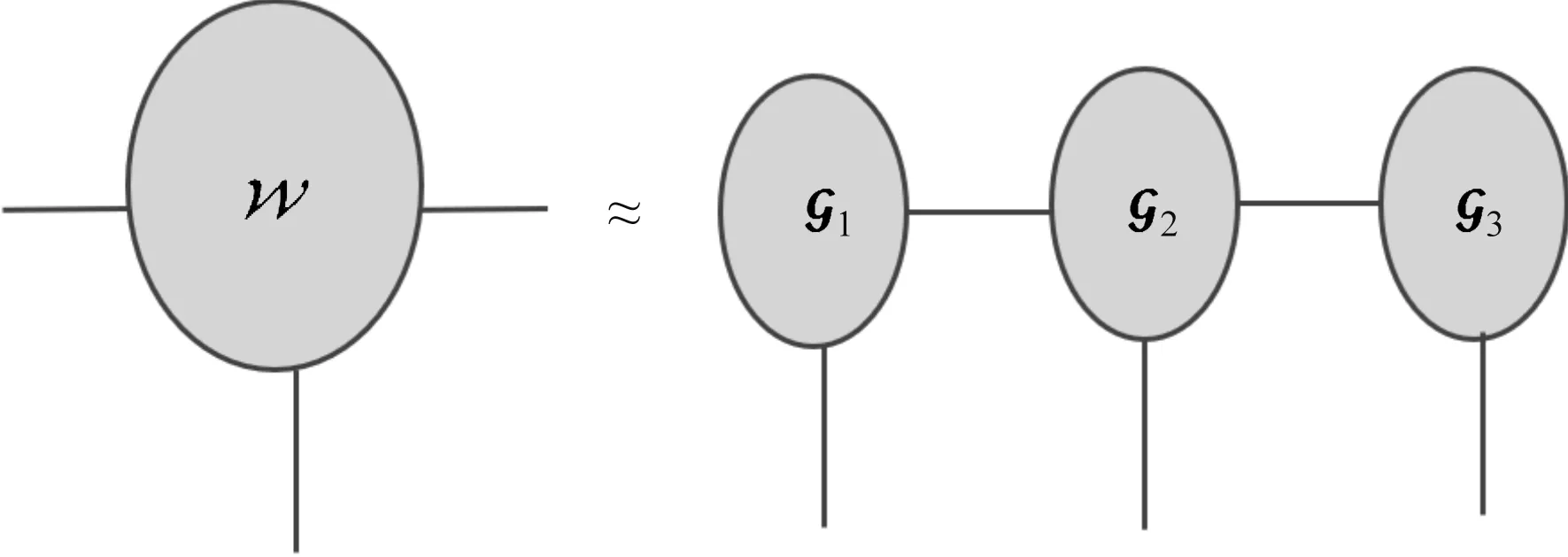
图6 权重张量的TT分解

2.3 参数张量化

张量网络包括以下的线性变换函数：

y=wx+b

(5)

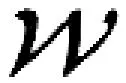
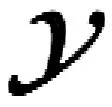
(6)

2.4 张量GRU网络

张量GRU网络表示如下：

(7)

式中，zt表示更新门，决定进入t时刻的信息。rt是重置门，决定丢弃多少信息，两者共同决定隐藏层ht的值。TL对应于不同的张量分解方法组成的目标函数，“∘”表示向量之间乘积。综上，可以得到CP-GRU，Tucker-GRU，TT-GRU张量网络模型。

3 实验结果与分析

为了评估张量网络识别准确率及其压缩参数的能力，在pytorch实验环境中，通过多脑运动想象脑电数据重复进行5次实验，分析比较张量网络识别准确率和压缩参数的效果。

3.1 单个被试和多脑的识别准确率对比

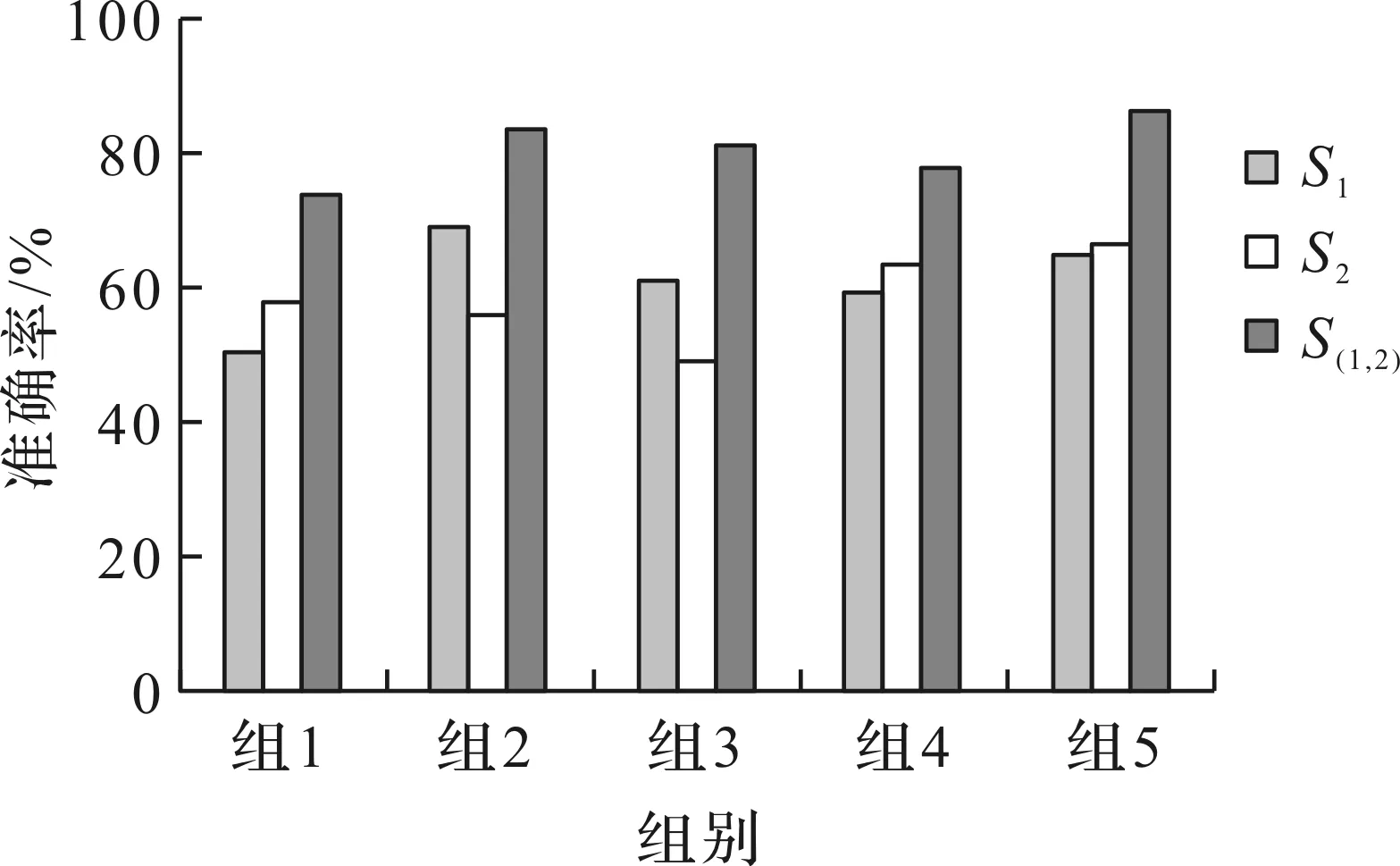
图7 每组被试识别准确率

对单个被试、多脑融合数据重复进行5次实验得到平均识别准确率，结果如图7所示。图7中，S1，S2分别表示同一组中2名被试的识别准确率，S(1,2)表示2名被试数据融合后的识别准确率。从图7可以看出，多脑融合数据识别准确率普遍比单个被试高，最高可达86.6%，提高了17.2%。与传统的CSP方法[6]相比识别准确率提高了2.8%，张量网络能够识别更多的特征信息，从而提高了准确率。

3.2 不同模型的识别准确率和参数量对比

实验采用GRU模型作为对照组，选择不同的秩运行CP-GRU，Tucker-GRU，TT-GRU模型，实验结果如表1所示。与GRU模型相比，CP-GRU，Tucker-GRU，TT-GRU模型的识别准确率都有所提高，参数数量均小于GRU模型。与其他3种模型相比，TT-GRU模型的识别准确率最高。

4 结束语

本文提出一种基于张量网络的多脑运动想象数据识别方法。在神经网络参数众多的情况下，使用张量分解方法来压缩神经网络中权重张量的参数数量，提高了张量网络的识别准确率。但是，本文实验样本较少，后续将采集更丰富的样本，增加对比组的分析，得到更有说服力的结果。