基于随机矩阵和能量双联合的协作频谱感知

石 新，刘顺兰

(杭州电子科技大学电子信息学院，浙江 杭州 310018)

0 引 言

随着无线通信技术的快速发展，多媒体业务呈指数型增长，有限的频谱资源变得越来越稀缺，但是，很多频谱资源的利用率并不高。面对这个问题，Mitola博士在1999年提出了“认识无线电”的思想，通过对频谱空洞进行感知，在次级用户不影响主用户通信的情况下，接入主系统进行通信[1]。传统的频谱感知技术主要以能量检测[2]、匹配滤波器检测[3]和循环平稳特征检测[4]为主，其中能量检测技术因不需要知道信号的先验信息，复杂度较低，广受关注，但能量检测技术受噪声的影响较大。随着随机矩阵理论的发展，文献[5-6]提出了两种新型的频谱感知算法，最大最小特征值之比(Maximum Minimum Eigenvalue，MME)算法和最大最小特征值之差(Difference between Maximum and Minimum Eigenvalue， DMM)算法，在低信噪比下，获得较高的检测概率，但检测速率较慢，同时门限阈值服从Tracy-Wisdom分布，没有固定的分布函数，使用时需要查表取值，不够灵活。文献[7]对MME算法进行改进与优化，使门限阈值服从正态分布，能准确计算门限值。针对上述频谱感知技术的不足，本文提出随机矩阵和能量双联合协作频谱感知算法(本文简称RMED算法)，在优化MME算法的基础上，联合能量检测算法进行频谱感知。算法既保留了能量检测算法和MME算法的优势，又提高了检测概率和检测速率，具有良好的感知性能。

1 RMED频谱感知系统模型

RMED频谱感知系统模型如图1所示。模型由2个次级用户(the Secondary User ，SU)和1个主用户(the Primary User ，PU)组成。RMED频谱感知系统的作用是在不干扰主用户正常通信的前提下，2个次级用户SU1和SU2进行协作感知，借助频谱空穴进行通信。假设系统信道为瑞利衰落信道，SU1和SU2各自对来自PU的信号进行感知与判决，将判决结果发送给融合中心(Fusion Center, FC)，FC根据AND准则进行最终判决。判决为H1，表示频谱繁忙，主用户使用该频谱；判决为H0，表示频谱空闲，主用户未使用该频谱。

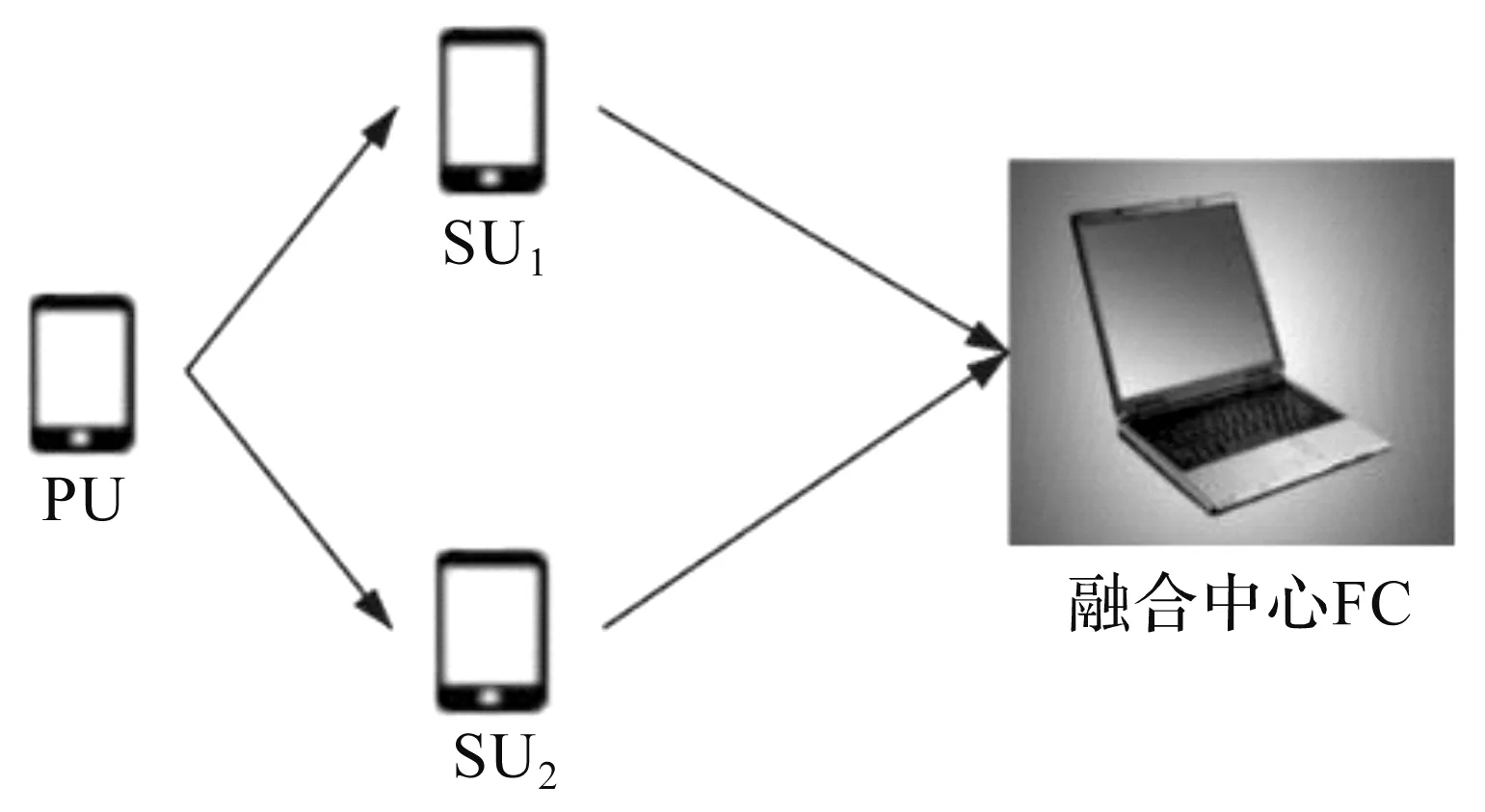
图1 RMED频谱感知系统模型

根据统计学中的二元假设模型，SUi接受信号可表示为：

(1)

式中，i=1,2，yi(k)为SUi接收到信号，xi(k)为待测的PU信号，hi(k)为SUi接收信号的路径损耗因子，wi(k)表示加性高斯白噪声，其均值为0，方差为σ2。

2 RMED频谱感知算法

SUi对接收到的信号进行奈奎斯特采样，其接收信号为yi(k)。根据SUi接收到的信号，计算其能量统计量E：

(2)

将统计量E与门限值γ1进行判决，若统计量E比门限值γ1大，则判决结果为H1，表示主用户繁忙，不存在频谱空穴；若统计量E比门限值γ1小，则计算信号的协方差矩阵，求出特征值并加以分析。根据式(1)，L个连续抽样信号向量表示为：

Yk=[yk,yk-1,yk-2,…,yk-L,yk-L+1]T

(3)

Xk=[hkxk,hk-1xk-1,hk-2xk-2,…,hk-Lxk-L,hk-L+1xk-L+1]T

(4)

其中，L为平滑指数，yk为SU接收的样本信号，xk为PU发送的样本信号。按照采样数N对SUi进行采样，得到矩阵Yk的维度为L×N：

(5)

接收信号的采样协方差矩阵RY(N)的维度为L×L：

(6)

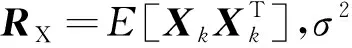
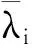
(7)

式中，i=1,2，γ2为判决门限值。

SUi将各自的判决结果发送给融合中心，融合中心根据AND准则，进行最终的判决。

RMED频谱感知算法的具体步骤如下。

(1)次级用户各自对接收信号进行奈奎斯特采样。

(2)根据虚警概率，设置合适的判决门限γ1和γ2。

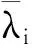
(4)融合中心依据AND准则，对接收的结果进行最终判决。

3 RMED频谱感知算法的门限值和虚警概率分析

RMED频谱感知算法由能量检测算法和改进的MME算法两部分构成，假设能量检测算法的虚警概率为Pf1,门限值为γ1，改进的MME算法的虚警概率为Pf2,门限值为γ2，则RMED频谱感知算法的虚警概率Pf表示为：

Pf=Pf1+(1-Pf1)Pf2

(8)

由式(8)可知，对于固定的Pf，Pf1和Pf2有多种不同的组合来实现。当Pf1过高时，RMED算法的Pf主要由能量检测部分决定，在一定程度上降低了RMED算法的运算量，提高了检测速率，但改进的MME算法部分却降低了低信噪比情况下的检测概率；相反，当Pf1过低时，RMED算法主要由改进的MME算法部分决定，在一定程度上增加了RMED算法的复杂度，但也提高了检测概率。针对上述问题，需采用一个折中的办法，令Pf1=Pf2，则有：

Pf=Pf1+(1-Pf1)Pf2=2Pf1-P2f1

(9)

(10)

对于能量检测算法部分门限值γ1，可根据传统能量检测门限计算公式[8]求得，即

(11)

(12)

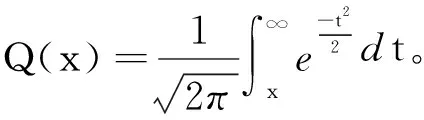
对于改进的MME算法部分门限值γ2进行分析。

由M-P定理可知，对于一个L×N的矩阵B，其中元素满足独立同分布[9]。当L→∞,N→∞时，L/N→α(0<α<1)，则矩阵B的最大特征值表示为：

(13)

根据式(6)可知，当主用户处于H0状态时，只有加性高斯白噪声，则RX=0。SUi接收到的信号平均能量表示为：

(14)

则有：

(15)

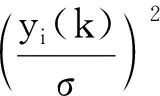
(16)

由式(14)和式(15)可得：

(17)

由式(10)、式(13)及式(17)可推导出虚警概率Pf2：

(18)

根据式(10)和式(18)，得到门限值γ2：

(19)

4 仿真实验结果与分析

仿真环境由1个主用户和2个次级用户组成，采样点N=512，信号采用二进制相移键控(Binary Phase Shift Keying，BPSK)调制。SU1到PU的距离为0.5，SU2到PU的距离为0.9；融合中心FC采用AND准则进行最终判决。分别采用RMED算法、能量检测算法、MME算法、特征值改进算法[7]进行1 000次Monte Carlo仿真，从信噪比、虚警概率概率、采样点数以及检测速率等4个方面来分析4种算法的感知性能。

信噪比为-12 dB，虚警概率范围为0.01～0.50，以0.05的速率变化时，4种算法在不同虚警概率下的检测概率结果如图2所示。从图2可以看出，随着虚警概率的逐渐增大，检测概率逐渐增大，其中RMED算法的检测性能明显优于其他算法，在低虚警概率的情况下，检测概率大约提升了43%。

采样点数为512，虚警概率Pf=0.01，信噪比范围为-15～0 dB时，4种算法在不同信噪比下的检测概率结果如图3所示。从图3可以看出，RMED算法检测性能最优。RMED算法检测性能远远强于能量检测算法。在低信噪比情况下，RMED算法的检测概率强于文献[7]的特征值改进算法；随着信噪比的增加，检测概率也逐步增加，当信噪比为-7 dB时，RMED算法、文献[7]特征值改进算法、MME算法的检测概率基本接近1。能量检测算法的感知性能相比其他算法差距过大的原因在于该算法受噪声影响较大，在信噪比为-4 dB时，检测概率才接近1。

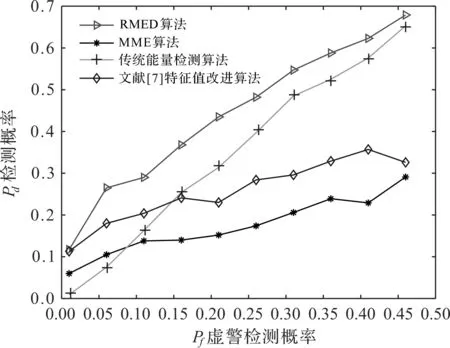
图2 不同虚警概率下，4种算法的检测概率

图3 不同信噪比下，4种算法的检测概率

不同采样点数下，虚警概率Pf=0.01，信噪比范围为-15～0 dB时，4种算法在不同采样点数下，不同信噪比的检测概率结果如图4所示。从图4可以看出，随着采样点数的增加，4种算法的检测概率都在逐步提升，但RMED算法检测概率的提升幅度明显比MME算法和能量检测要快许多。当采样点数为1 024时，RMED算法在信噪比大于-12 dB时，检测概率接近1，其他2种算法在信噪比大于-9 dB时，检测概率才接近1。采样点数越大时，相比MME算法和能量检测算法，RMED算法具有更好的频谱感知性能。当采样点数为512时，RMED算法的检测概率优于文献[7]特征值改进算法，在采样点数为1024时，2种算法的曲线走势基本一样。由此可以看出，在低采样点情况下，RMED算法比文献[7]特征值改进算法具有更好感知性能，检测概率大约提升了2%。

在不同信噪比情况下，4种算法的检测时间如图5所示。由图5可以看出，信噪比小于-5 dB时，相比其他3种算法，能量检测算法的检测效率最高；信噪比小于-11 dB时，文献[7]特征值改进算法、MME算法的检测效率高于RMED算法。这是因为RMED算法由两部分构成，在信噪比小于-11 dB时，RMED算法以改进的MME算法部分感知结果为主，即先进行能量算法部分感知，再进行改进的MME算法部分感知，导致检测效率低下。但是，随着信噪比的增加，RMED算法逐渐以能量检测算法部分为主，检测效率逐渐增加，在信噪比大于-11 dB时，检测效率优于MME算法和文献[7]特征值改进算法，在信噪比为-4 dB时，检测速率提升到最大，大约提升了52%。在信噪比大于-5 dB时，基本与传统能量检测算法的检测效率一样。

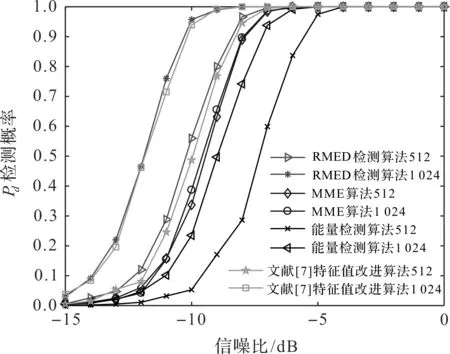
图4 不同采样点数下，4种算法在不同信噪比的检测概率

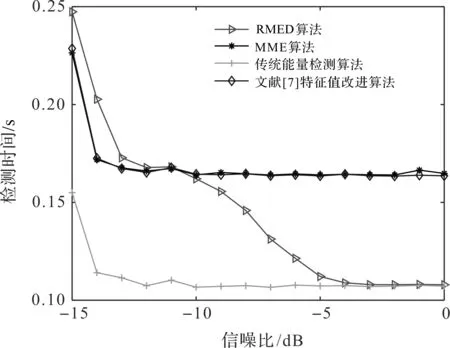
图5 不同信噪比下，4种算法的检测时间

通过以上分析可以发现，相比于其他3种算法，RMED算法在保证较高检测概率的同时，一定程度上提高了检测速率。在低虚警概率、低采样点数的情况下，RMED算法的检测概率最高。

5 结束语

本文提出一种随机矩阵和能量双联合频谱感知算法，利用能量检测算法和改进MME算法的互补关系进一步提高了检测概率和检测效率，在保证检测概率的同时，缩短了检测时间，更加适合未来复杂环境的无线通信。但是，本文算法复杂度较高。后期研究中，考虑将数学理论运用到频谱感知算法中，比如将本文中的随机矩阵理论替换成哈达玛矩阵理论，进一步降低算法复杂度，提高感知性能。