非牛顿流体减速带二次优化方案∗

陈波佑 陈亦新 张双焱

（长安大学公路学院 西安710021）

1 引言

近几年非牛顿流体凭借其特性在国内外工业领域得到了广泛的应用［1，9，15］，这种材料的二次开发也逐渐普及到了各个工程行业中，这种流体因为其剪切速率与剪切应力之间存在着一定的关系，即其根据速度梯度不同分为胀塑性（剪切增稠）流体、假塑性（剪切稀化）流体以及理想流体。非牛顿流体的流变性能和流变规律较为复杂，不同类型的非牛顿流体呈现出不同的流动曲线［1］，如图1所示，其中假塑性流体则当其剪切速率γ由0→γ1时，剪切黏度保持常数，而当γ由γ1→γ2时其剪切粘度降低，此后流体剪切粘度趋于一个定值，概括其流动规律即在稳定的剪切流动下，其流体粘度随着剪切速率的增加而减少。

图1 五种非牛顿流体流动曲线

当前国内减速带的现状为主要有道钉减速带、驼峰减速带、水泥台减速带、路面凹形槽减速带等，其实这些减速带共同的作用［2~3］就是通过改变道路某段的高度或材料，根据心理、生理原理［2，8］即当机动车以较高车速通过减速带时，产生的振动会从轮胎经由车身及座椅传递给驾驶人，垂直曲线将产生一个垂直方向的加速度，进而产生强烈的生理刺激以及心理刺激，降低了驾驶人对道路环境的安全感从而强制机动车减速，以达到安全的目的。但这么做不仅让驾驶员的驾驶体验在通过减速带是因产生的颠簸感而降低，而且规格固定的减速带对于国内多种车体无法全面适配，容易出现过带时损坏底盘的现象，且司机因心理作用在过减速带时单侧通过减速带，这会造成车身倾斜，受力不均，会对车辆造成一定损坏。

对此问题国外研究者发明了一种新型智能减速带，这种减速带内含非牛顿流体，由于假塑性流体在较低剪切应变速率的变化过程中其剪切应力变化幅度大，而其他非牛顿流体则由于自身流动性质原因难以在较低车速或别的因素下迅速变换自身结构，因此考虑使用假塑性流体用于减速带的填充物，在机动车以较高速度通过这种减速带时，由于假塑性流体流动特性，流体会呈现固化现象，以此来达成一般减速带的减速作用，而在车速较低的情况下假塑性流体内部的切应力较低，呈现出流动现象，机动车可以平稳通过，底盘元器件也不会因为震动而受损，同时驾驶员的过带舒适度也会提升。

这样的非牛顿流体减速带便拥有着提高行车安全及过带舒适度的可行性，不过这种智能减速带因内含流体的量没有一个标准或范围导致载重量大的车辆通过时会出现含液体多的减速带刚度失效的可能，同时含液体量低的减速带无法起到抑制快速汽车的作用。同时在生产中，这种流体减速带需要在路面上固定住，其内部的温度便成为了影响减速带的重要指标之一，并且为了保障减速效果，其内填充流体的填充量也是需要考虑的核心问题之一，研究填充量则对非牛顿流体减速带的泛用性的提升有着重要的意义。

文中将对假塑性流体的特性展开进一步的研究，进而分析计算得出填充量与温度及车速之间的关系并研究出一种计算不同温度下的保证减速效果的临界车速的算法，给生产过程提供理论参考。

2 建立理论模型

在道路上常见的两种减速带即梯形截面和椭圆形截面驼峰减速带中，实验［3，12］证明，机动车通过椭圆形截面减速带速度减少量明显大于通过梯形截面减速带的速度减少量，且在通过椭圆形截面减速带后大范围减速的比例要比通过梯形减速带后的减速比例大。考虑实际生产问题，为提高减速效果，减速带模型采用类椭圆形截面。

当车速达到v0即使减速带呈现为刚体时车轮接触减速带时，在理想情况下根据力的作用效果将减速带提供给车轮的支持力F进行正交分解。水平方向有：

竖直方向有：

其中Δvx指汽车在接触减速带的过程中速度水平方向的分量，从上式分析可得机动车在此情况过带时收到刚体化非牛顿流体减速带给予的力的效果体现在F1的大小和Δvx的大小上。简化模型图［2］如图2所示。

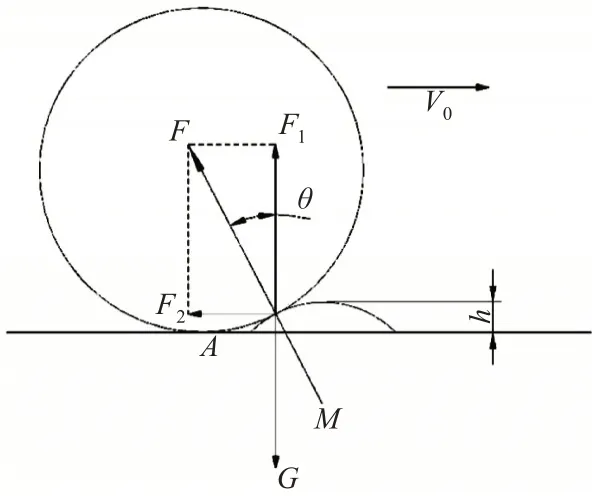
图2 非牛顿流体（刚体状态）受力简化模型

为简化计算，将确定减速带内部假塑性流体的含量多少转化为h的大小，在一定h值下减速带能对机动车产生的作用反映在F1的大小上，F1越大说明机动车过带时震感越明显，Δvx越大说明理论减速效果越佳由几何关系易得h与θ之间的函数关系为

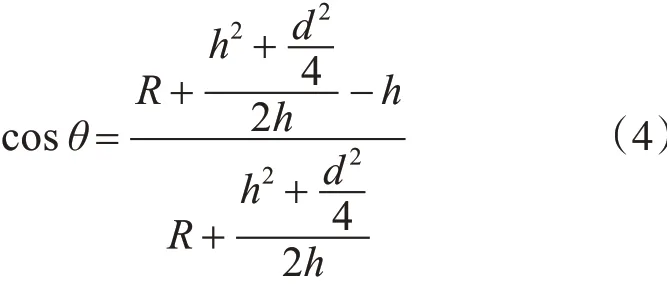
其中R为车轮半径，d为减速带宽度。

要确定h的值需要对F进行分析，根据实验得出生产中认为水泥生浆为符合幂律模型的假塑性流体，这种流体不具备结构性［4，6］，在关内阻力分布与牛顿流体相同其本构方程如下：

对式（5）移项可得：

等式左右同时积分得：

其中τ为切应力、m为流变指数、ηe为稠度系数（ηe是粘度的度量，但数值上不等于粘度值）、h0为静态时减速带的垂直高度。

在实际情况下想要获得切应力大小与相关参量之间的关系时涉及因素较多，难度较大因此可以选用控制在一定条件下的两个相关参量之间的拟合关系来描述［4，13］。对于式（7）而言，要确定的物理量仅为m与ηe，由幂律流体的性质［7］得知其流变指数与稠度系数皆与温度T相关，已有学者通过旋转粘度计较为精确地测得了一组温度与基本参数的数据［5］，如表1所示。

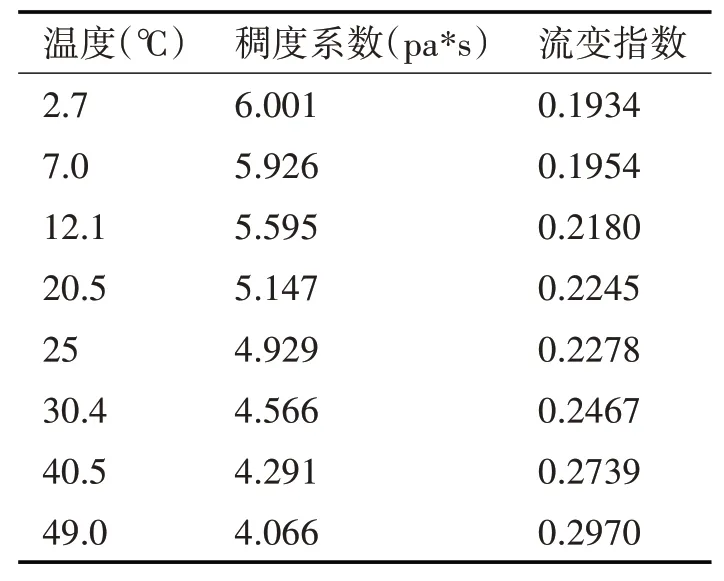
表1 温度与稠度系数和流变指数关系

对表1中的数据进行数据分析，在进行多项式拟合时不宜采用高次多项式拟合［5，10］，阶次太高会产生龙格现象，即在已知点数据误差为零，但点之间可能会有很大的误差，曲线表现为全部穿过已知点，但有很大的振荡。在不断试验中选用5次多项式拟合稠度系数与温度之间的关系曲线，拟合效果如图3所示。

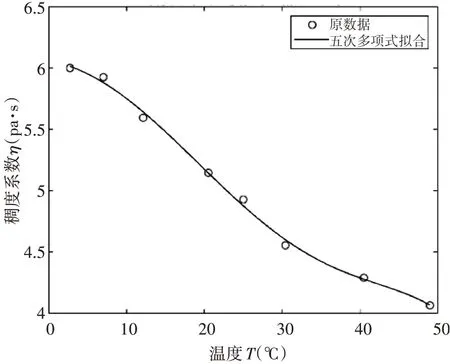
图3 稠度系数η与温度T的关系

此时拟合结果得出的自由度、残差范数如表2所示。

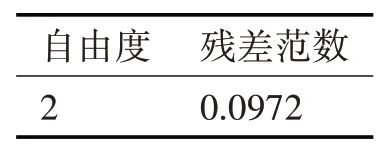
表2 稠度系数与温度多项式拟合误差估计

由结果可以分析得出拟合效果较好，残差范数较低，且得出ηe与T之间的关系式为

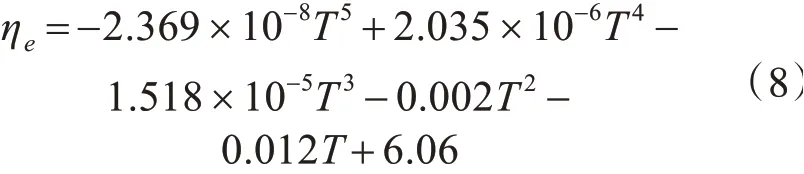
同理可以得到流变指数与温度的5次多项式拟合曲线如图4所示。

图4 流变指数m与温度T的关系

此时拟合结果得出的自由度、残差范数如表3所示。

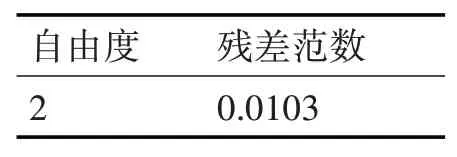
表3 流变指数与温度多项式拟合误差估计

得出m与T之间的关系式为

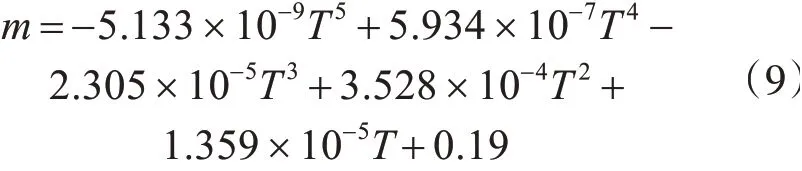
3 仿真研究

基于Matlab平台进行仿真研究［13~14］，在研究h的合适值时应采用控制变量法，由式（5）可得在理论计算中需要控制的变量为温度T，为简化计算探寻规律，采用低温、常温、高温三种环境温度进行研究并认为流体温度等于环境温度。温度数据来源于2019年西安市的全年温度曲线图，低温T1=-3℃、常温T2=25℃、高温T3=35℃，根据式（8）及式（9）得出三种温度下的流变指数和稠度系数，如表4所示。

表4 三种温度下的流变指数与稠度系数

以下分三种情况进行讨论：

低温环境下，得到幂律流体本构方程为

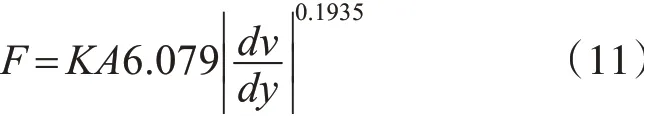
同理，常温环境下有：

高温环境下有：

其中K涉及因素较多需要根据实际情况判断取值，现认为减速带变形程度dy≤0.001m时呈现刚性，得到如下关系式：

临界情况下Fcosθ=G，已知生产减速带的企业生产时，有一个较为统一的标准［11］：减速带宽度不得超过30cm，垂直高度不得超过5cm。现取机动车重量为1500kg，即G=7500N，K=36000［1］。设机动车轮胎外半径R=0.3m，减速带宽度d=20cm，车胎与减速带接触面积A=80cm2联立式（4）、（14）进行三次多项式拟合得出三种温度下v0与h关系如图5所示。

图5 三种温度下v0与h拟合关系

拟合曲线的多项式结果如下：35℃时有：

此图说明的是在保证减速效果生效的情况下减速带内部的填充水泥生浆量与过带瞬间车速之间的关系即得出在不同温度下，可以得到相同水泥生浆填充量即相同垂直高度下，低温环境中使减速带减速效果生效的临界车速最高，高温环境下的最低，三种温度下的临界车速及相互间的差值随着减速带垂直高度的提升而提升；相同临界车速下，要使减速带减速作用生效，高温环境需要填充的水泥生浆最多。总体上看，使减速带的减速作用生效临界车速受其内流体温度影响交大。

若驾驶员遵守交通规则慢速通过，非牛顿流体会呈现流动现象，从原有的高度h受压降低，已有文献说明以现有的车辆减振装置系统判断减速带降低25mm~40mm（具体数值根据实际生产时的减速带垂直高度确定）时，人过带时产生的震感和不适感会极大的下降，汽车可以平稳地通过减速带。此时根据式（7）得出需要满足的条件为

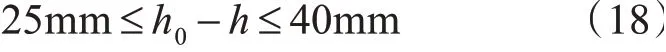
此时30mm≤h0≤50mm，采用推理的方法进行分析，设置h0-h=30mm，温度条件为25℃，机动车过带时的车速为1.5m/s，其余条件不变，联立式（3）、（4）、（7）、（14）得到F1与h0的关系图如图6所示。

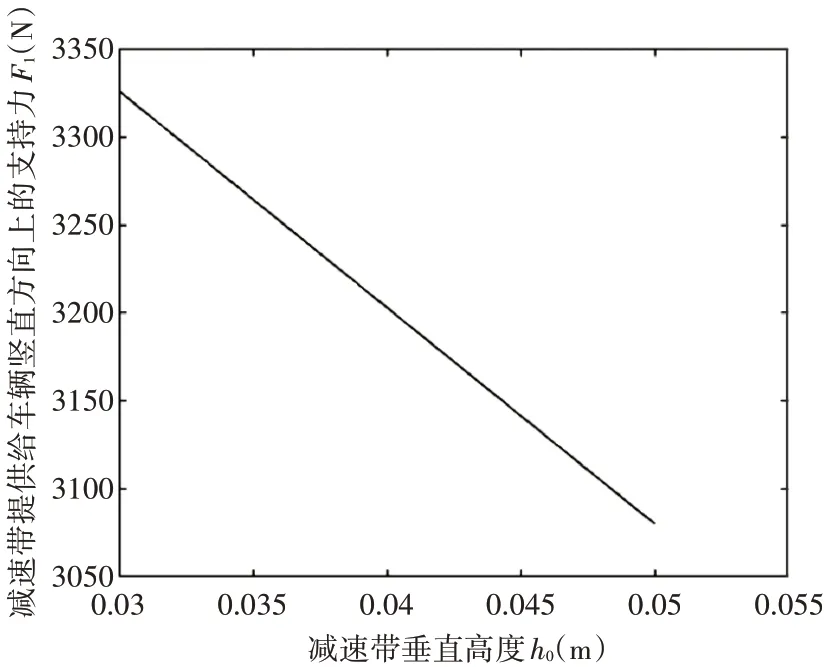
图6 常温条件下h0与F1理论线性关系

由图6分析可得增加减速带垂直高度理论上可以降低震感即F1的大小。

4 结语

1）在实际生产这种非牛顿流体减速带时需要将当地气温作为重要指标考虑进去，进而考虑减速带具体宽度，通过来往车辆的平均重量、车胎与减速带接触面积的平均值、车辆过带的平均速度、车辆平局底盘高度以及修正系数等因素来确定减速带的垂直高度即非牛顿流体的填充量。

2）经过仿真研究可知理论上非牛顿流体的填充量在满足实际需求的情况下越多，汽车在过带时的速度范围更大，相同的较低速度下非牛顿流体填充量多的减速带降低驾驶员震感提高其过带舒适度的效果更佳，但过多的填充量会造成低温环境下保证减速带减速效果的临界车速过高，汽车在过带时的减速效果不能得到保障，因此确定合适的填充量需考虑多方边界条件。

3）该研究提供了一种计算非牛顿流体减速带填充量的理论算法，但在实际情况下这种非牛顿流体减速带的性能还与覆盖面材料、覆盖面的导热性等因素相关，并且流体减速带受压时情况较为复杂，因此论文还存在一定局限性，今后可以在考虑非牛顿流体减速带覆盖面与流体之间的热交换及受压时存在的耦合现象的基础上进一步展开研究，以提高结果的精确性。