带LC滤波器的UPS三电平NPC逆变器改进模型预测控制∗

吴 拓 庞科旺 经鹏宇

（江苏科技大学电子信息学院 镇江212000）

1 引言

在过去几十年里，功率变换器在很多领域都有着良好的应用效果，如能源转换、传动装置、分布式发电系统等，功率变换器的控制方案得到国内外学者的广泛研究［1］。文献［2~4］给出脉宽调制在逆变器中的相关应用，也证实了控制方案的有效性。随着微处理器技术的发展、计算速度不断提高、功能逐渐增强，一些新的且更为复杂的控制方案得以实现。其中包括模糊控制、滑膜变结构控制等，文献［5~6］给出模糊控制在逆变器中的应用。智利Ro⁃driguez R教授将FCS-MPC应用于电机控制、并网逆变器等，取得了很好的控制效果［7］。与传统控制器相比，模型预测控制没有复杂的参数整定，对系统多约束条件易于实现，控制过程非常灵活，具有非常强的鲁棒性，因此，MPC非常适合对大功率变换器的控制［8］。

在UPS系统中，通过逆变器输出端加入LC滤波器来提高系统性能，以满足对电能质量要求较高的场合。由于系统运行时对数据采样以及算法计算存在一定时间，将其定义为系统延迟时间，该延迟会导致实际值与预测值之间存在偏差，使系统达不到理想控制效果［9］。针对传统FCS-MPC存在的延迟问题，文章采用一种改进模型预测控制，用两步预测代替一步预测，使预测系统在当前采样时刻便确定下一采样时刻的最佳开关状态组合。文章通过仿真对不同负荷下输出电压波形、THD值等性能指标与传统单步预测进行比较，结果表明了该方法的良好性能。

2 三电平NPC逆变器模型

2.1 逆变器结构原理

文章所采用的三电平NPC逆变器结构如图1所示，其中LC滤波器位于图中虚线框中，负载未知（可能为线性或者非线性）。

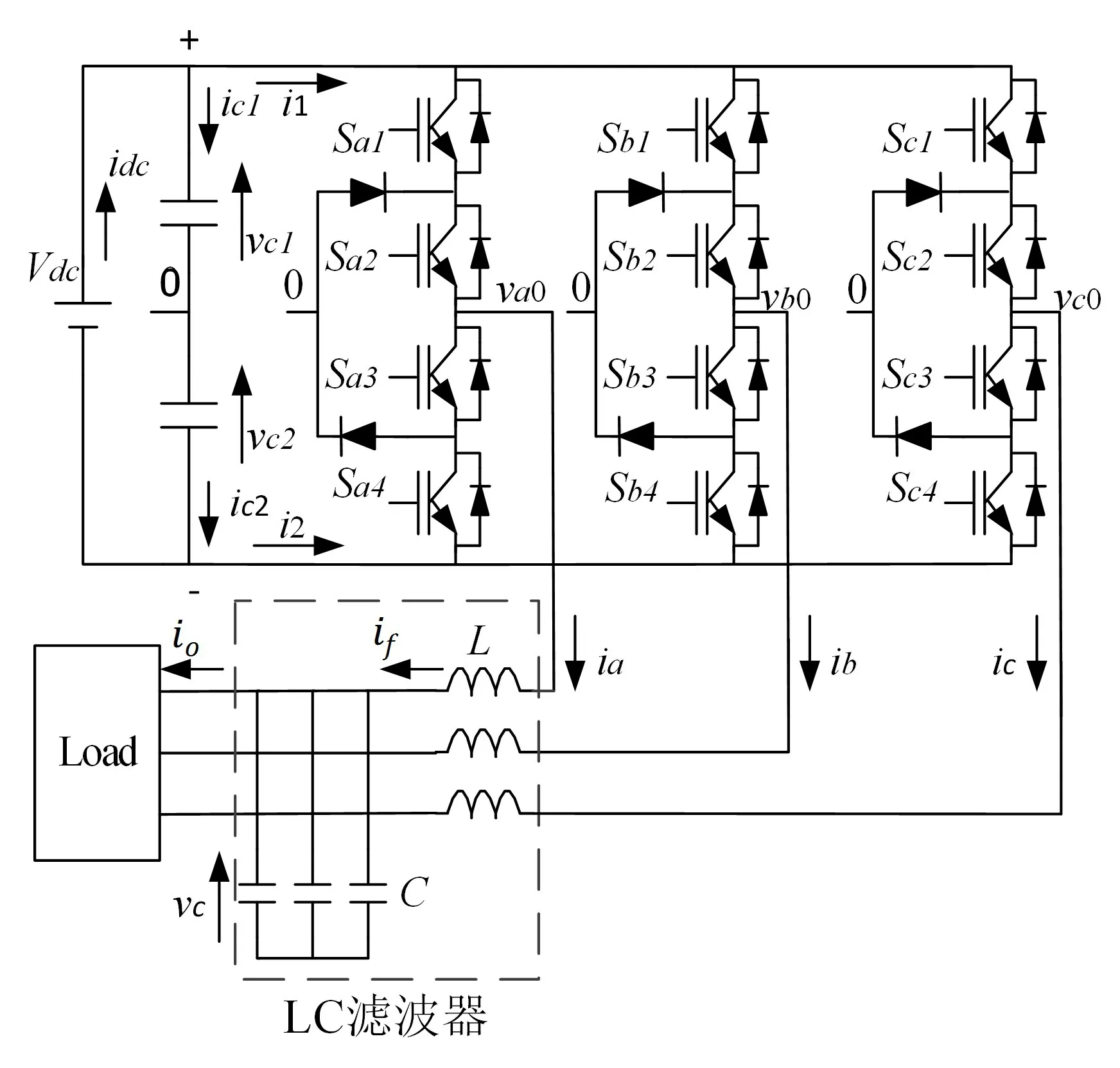
图1 逆变器系统结构图

若用x表示a、b、c三相，即x=｛a，b，c｝，则变量Sx表示x相开关状态，用+、-、0三种可能的状态值，分别代表逆变器输出相位中产生Vdc2、-Vdc2和0的开关组合，其中Vdc为直流侧电压。这里给出x相的开关状态表如表1所示。

表1 x相的开关状态表

考虑三相所有开关组合，共可产生33=27种开关状态，而不同的电压矢量有19种，如图2所示。

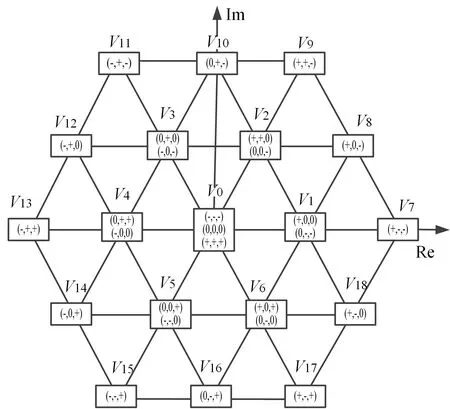
图2 逆变器电压矢量和开关状态

由输出电压空间矢量定义：

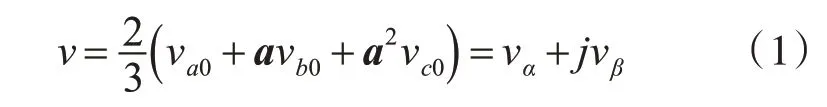
式中，a=ej(2π/3)，vα、vβ为v在两相静止坐标系α β下的分量。

对于滤波器电感电流if、电容电压vc、输出电流io用矢量可表示为

图3 给出LC滤波器模型，该模型可以用电感、电容两个差分方程进行描述。

图3 LC滤波器模型

式中，L为滤波电感，C为滤波电容。

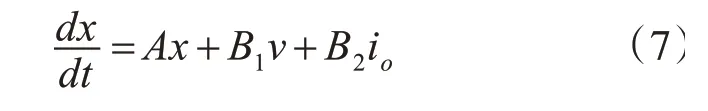
由图1可知，系统输出电压vo即为滤波电容两端电压vc，用状态方程表示为

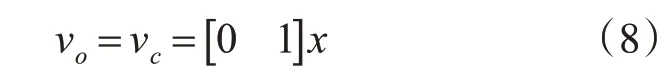
2.2 系统离散时间模型

给定采样时间Ts，由式（7）得到的系统的离散时间模型为

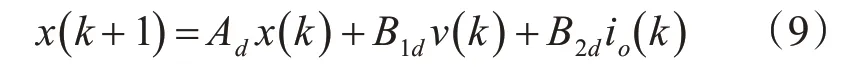
在图1中文章未给出具体负载特性，而利用式（9）对输出电压进行预测需要知道输出电流io的值，该值通常不进行测量，可由式（10）得到。

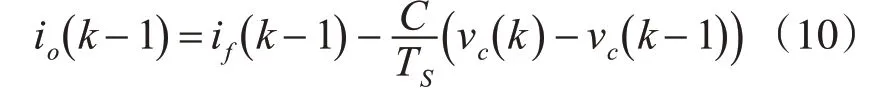
当采样时间TS很小时，我们可以假设负载电流在一个采样间隔不会发生很大改变，因而有

针对NPC逆变器，需要考虑中点电位平衡问题，不同的开关状态，对DC环节电容器而言具有不同的充放电效果。中点电位的不平衡会使交流侧输出电能产生低次谐波，输出电压发生畸变，严重影响系统性能和设备寿命［10］。文章通过对DC环节电容电压vc1、vc2离散化，得到其离散时间模型，并将其作为优化目标在代价函数中寻找最优解，即两者差值近似为零，以实现中点电位的平衡。

对电容电压vc1、vc2充放电的动态过程可以用以下差分方程进行描述。

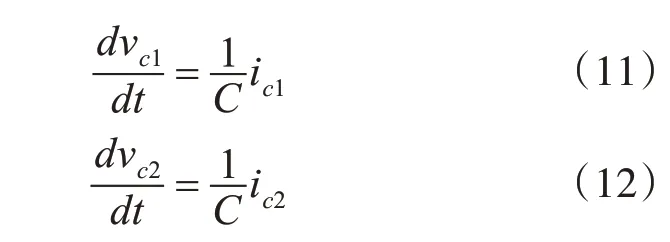
式中，C为电容值，ic1、ic2分别为流经两电容的电流。

文章采用前向欧拉法［11］对式（11~12）进行逼近，得到相应离散时间模型。

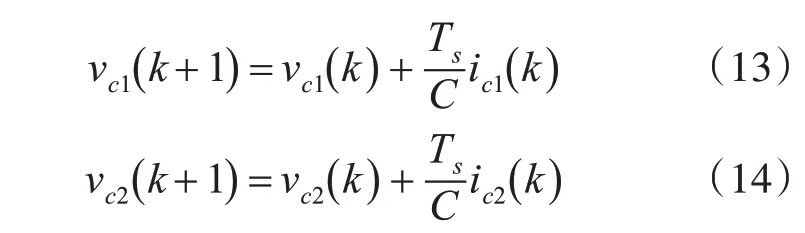
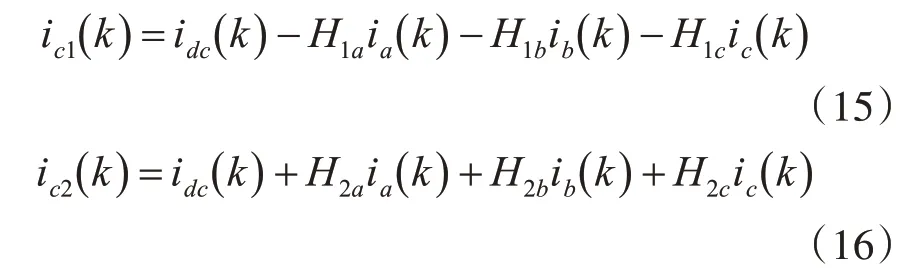
式中，idc为直流侧电压源所产生电流，开关状态H1x、H2x定义如下：

式中，x=a，b，c。

以上得到的离散时间模型即为控制器的预测模型。

3 改进模型预测控制器

3.1 模型预测控制

模型预测控制属于一种优化控制算法，通过代价函数对某一指标的最优化来确定未来的控制动作［12］。它一般由三个部分组成：预测模型、滚动优化和反馈矫正［13］，在系统受到外界不确定因素影响时，MPC可以利用滚动优化和反馈矫正环节进行补偿，从而提高系统的抗干扰能力和鲁棒性。

传统FCS-MPC实际为单步预测，控制过程如图4所示。图中，在每个控制周期预测得到的最佳开关状态组合如实线所示，而虚线代表着实际算法运行过程的开关状态组合。以S3为例，S3是模型预测控制系统在tk时刻得到最佳开关状态，若S3作用于tk时刻，则可达到预期效果，如图虚线所示，但实际S3作用时刻为tk+tz，tk+1时刻实际值为导致偏差的存在。延迟时间tz是系统进行数据采样和控制算法计算所带来的，由于这种偏差的存在，会直接影响系统的控制效果。

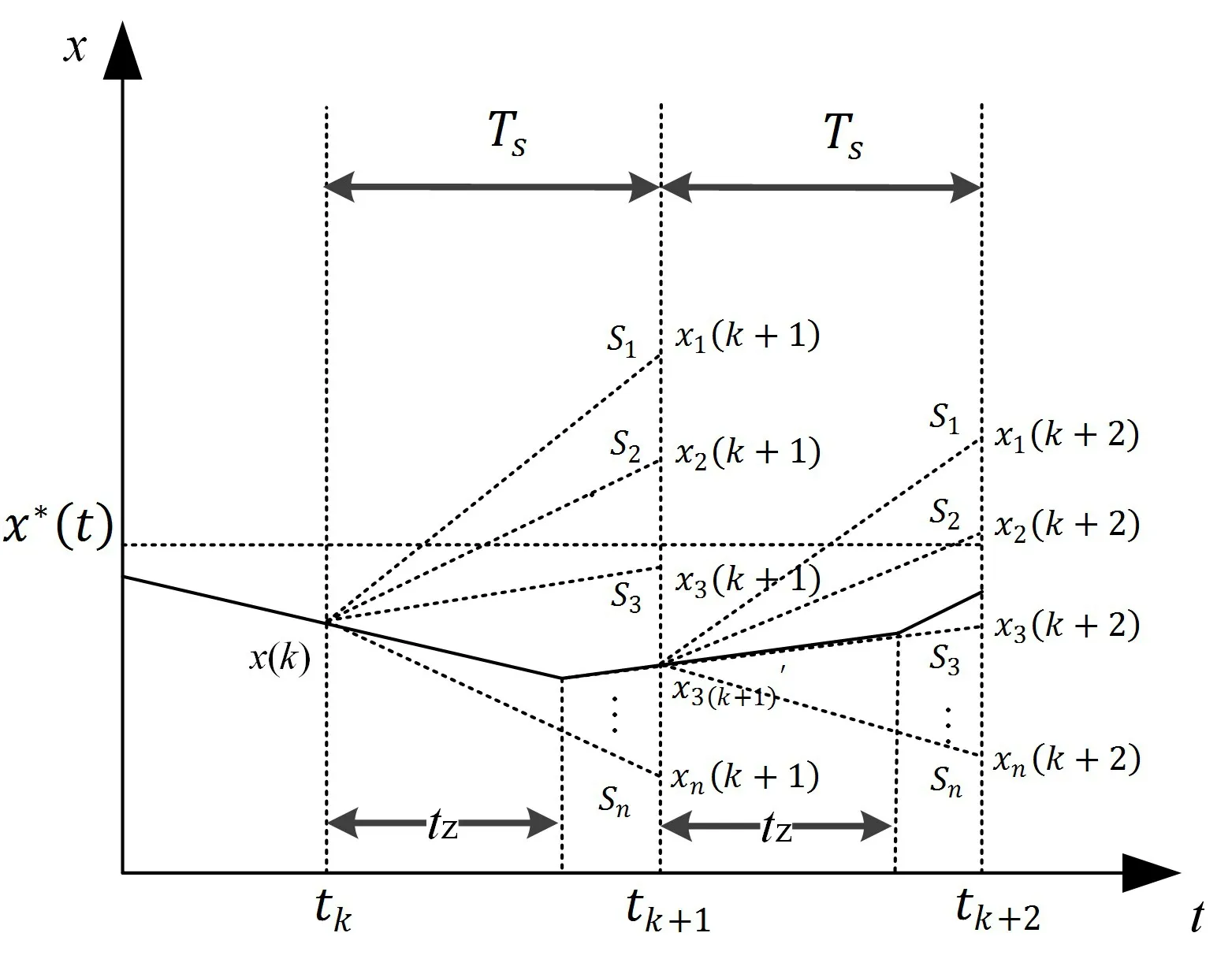
图4 传统FCS-MPC控制过程

为解决延迟对系统的影响，文章采用一种改进模型预测控制，用两步预测代替传统一步预测，其原理如图所示。在tk时刻通过采样计算得到tk+1时刻预测值，并在此基础上，以tk+1时刻预测值为测量值进一步预测tk+2时刻预测值，利用代价函数选择出最佳开关状态组合，并作用于tk+1时刻，从而在tk时刻就确定了tk+1时刻的开关状态组合。通过在三电平NPC逆变器中的应用，表明采用两步预测在不同负载下具有更好的控制效果。

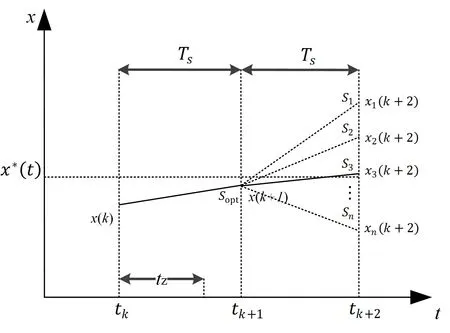
图5 改进MPC控制过程

采用两步预测的带LC滤波器的三电平NPC逆变器结构原理图如图6所示。

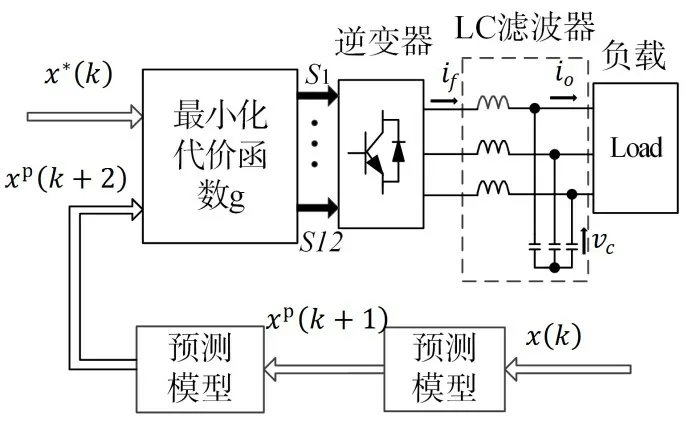
图6 改进MPC逆变器控制原理图

3.2 MPC代价函数

针对输出带LC滤波器的三电平NPC逆变器控制，文章主要实现两个目标：一是实现对给定电压的快速无差跟踪；二是实现对中性点电压的平衡。因此，在选择代价函数时，要能够实现对以上目标的控制。

文章给出代价函数g如下所示。

式中，v*

cα、v*

cβ为输出电压参考值在两相静止坐标系α β下的分量，为预测输出电压在α β下的分量，N为预测步数，λ为权重系数。

对于λ=0时代价函数，表示系统未将中性点电压的平衡作为目标优化，文章通过对λ=0和λ=0.1两种情况下DC环节电容器电压曲线进行仿真分析，结果表明在代价函数中通过设定权重系数λ，可以有效实现对中性点电压的平衡。

4 仿真分析

文章利用Matlab/Simulink工具对图1所示逆变系统分别在线性和非线性负载进行仿真，并与单步预测进行比较，来验证所采用控制策略的有效性及良好性能。

给出系统仿真参数如表2所示。

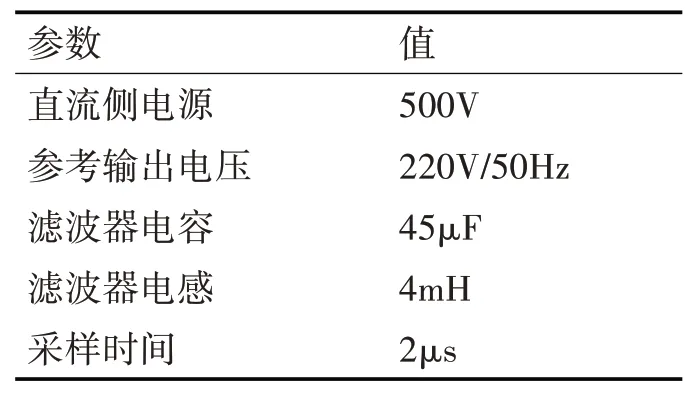
表2 系统仿真参数

针对线性负载，文章以纯阻性负载为例，对100Ω、1000Ω、1MΩ负载进行仿真，得到相应输出电压以及输出a相电压THD曲线图。传统FCS-MPC仿真结果如图7~9所示。

图7 100Ω负载下传统FCS-MPC仿真曲线

图8 1000Ω负载下传统FCS-MPC仿真曲线

可以看出，传统单步预测控制在负载较小100Ω时输出电压良好，畸变率小。在0.015s时THD值已达3%，0.027s时便降至1%以下，并逐渐趋近于零。但系统稳态时间以及THD值均随电阻变化有明显改变，1000Ω负载下，输出电压在0.1s才渐进正弦，而THD值在仿真时间内均在5%以上。1MΩ负载下，明显可以看出输出电压质量已经很差，THD值达到20%以上。

对相同电阻负载下，改进模型预测控制仿真结果如图10~12所示。

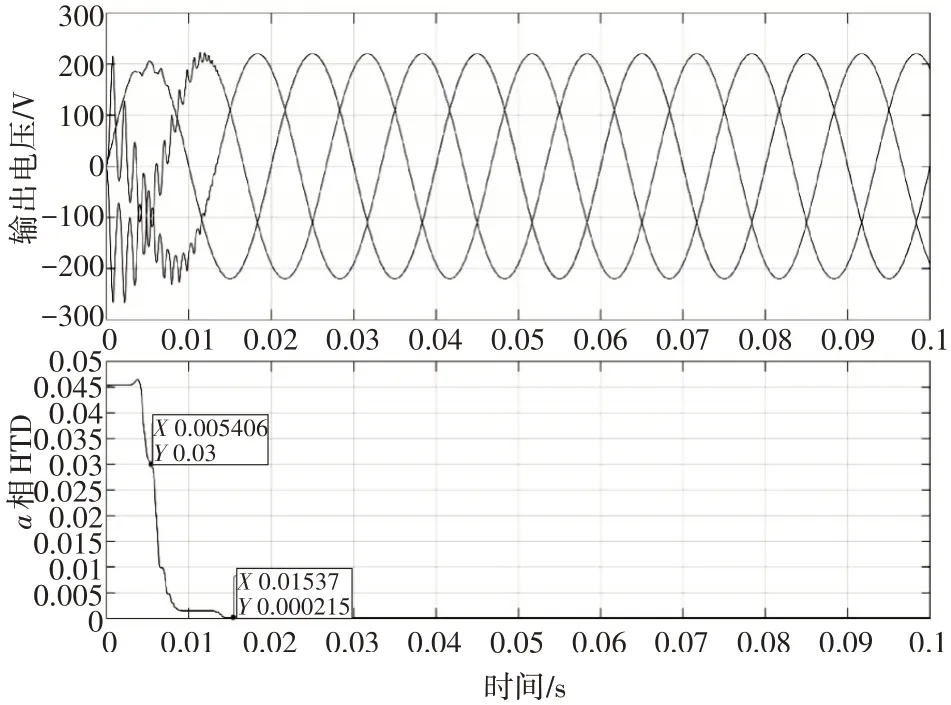
图10 100Ω负载下改进MPC仿真曲线

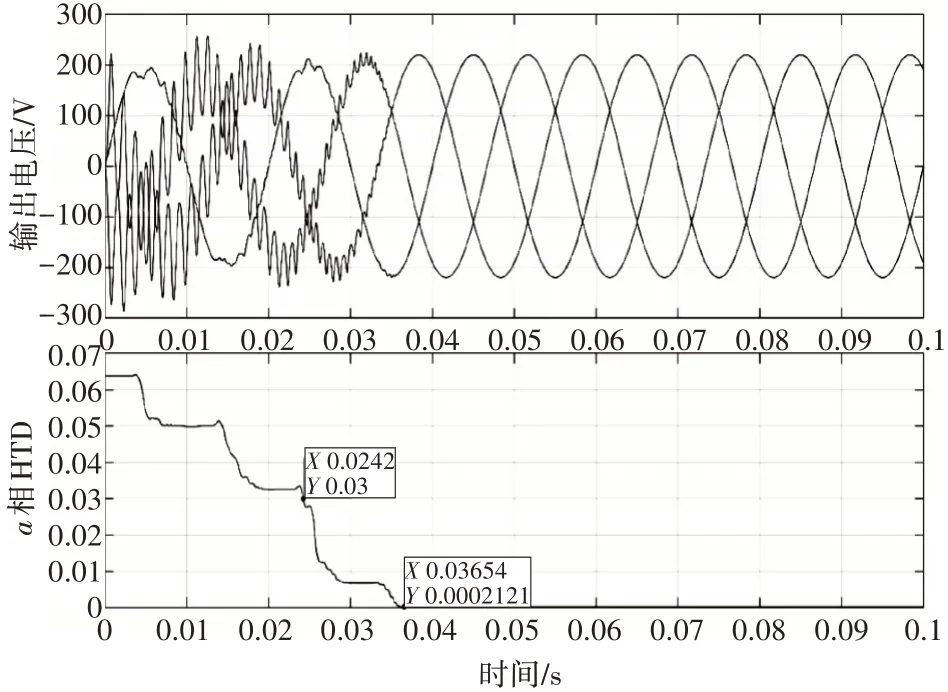
图11 1000Ω负载下改进MPC仿真曲线

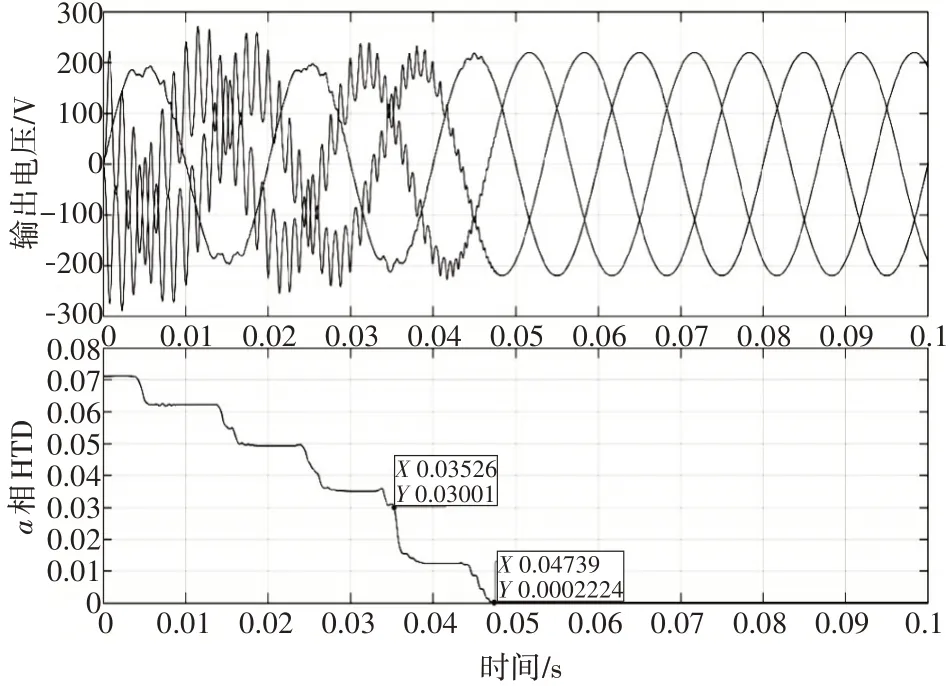
图12 1MΩ负载下改进MPC仿真曲线

可以看出，100Ω负载下，THD值在0.0054s便降至3%，仅约为0.27个周期。在0.015s时已趋近于零，可以认为电压为标准正弦波。1000Ω负载下，THD值在0.024s也降至3%，约为1.2个周期。1MΩ负载下，THD值在0.035s降至3%，约为1.75个周期。可以认为，在不同负载下都可以很快进入稳态，而且不同负载下的性能曲线十分相似，THD值最终都趋于零，意味着，不同负载下改进模型预测控制均可获得较高质量的输出电压，相对于传统单步预测，有较大性能提升。

针对非线性负载，文章给出一种三相不控整流电路如图13所示。

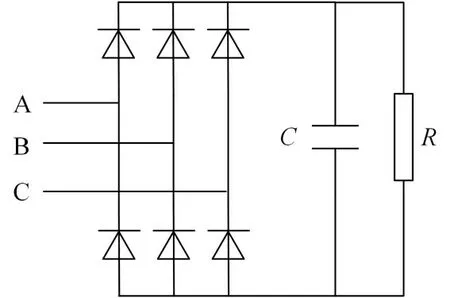
图13 三相不控整流电路

在整流电路R=100Ω、C=100μF下两种控制策略仿真图如图14~15所示。

图14 传统FCS-MPC仿真曲线

图15 改进MPC仿真曲线

从图中可以看出，传统FCS-MPC在非线性负载下稳态时间相对较长，在2.94s时THD值才达到3%，并逐渐减小。对输出电压也而言，2.94s之后正弦化程度越来越好。而改进MPC稳态过渡非常短，THD值在0.034s便已达到3%，仅约为1.7个周期，在0.048s时已趋近于0，系统特性与纯阻性线性负载非常相似。

针对改进MPC，表3~表4列出整流电路不同R、C值的仿真结果。

表3 R=100Ω，不同电容值

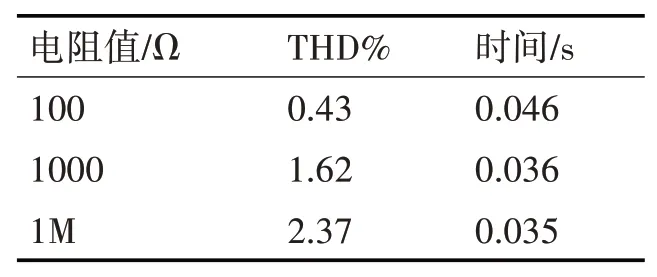
表4 C=1000μF，不同电阻值

另外，在改进MPC对中点电位平衡权重系数λ不同取值，仿真结果如图16所示。

图16 DC环节上下电容电压

从图中可以看出，通过在代价函数中加入权重系数λ便可方便实现对中性点电压的平衡，对给定直流侧电源500V，实现DC环节上下电容达到250V平衡，差值近似为0。

5 结语

文章针对带LC滤波器的三电平NPC逆变器提出一种基于两步预测的改进MPC控制策略，并与传统单步FCS-MPC进行比较，结果表明，改进MPC性能要优于传统FCS-MPC。无论线性还是非线性负载以及载荷大小变化，改进MPC稳态时间很短，两个周期（0.04s）内THD值便降至3%以下，并趋近于0，输出电压波形趋于标准正弦波，系统性能得到很大改善。