基于学生经验的数学教学理解与实践


【摘 要】研究者以2019年人教A版“函数y=Asin(ωx+φ)”为例,阐述对基于学生经验的数学教学的理解与实践,主张教学要基于学生已有的认知经验进行教学设计与组织,用好认知起点,激活思维,积累活动经验。
【关键词】学生经验;数学教学;理解与实践
【作者简介】丁益民,高级教师,全国新青年数学教师工作室创始人之一,主要研究方向为高中数学教材教法研究。
【基金项目】江苏省教育科学“十三五”规划课题“深度学习视域下高中数学单元教学设计与实践研究”(C-c/2020/02/50);苏州市“十三五”规划课题“高中数学中观教学设计与实践研究”(192110555) 一般認为,学生最有效的学习是在原有经验基础之上的再建构。奥苏贝尔说:“如果我不得不将所有的教育心理学原理还原为一句话的话,我将会说,影响学习的最重要因素是学生已经知道了什么,根据学生的原有知识状况进行教学。”[1]新课程改革关注学生发展,强调要以学生已有的经验为基础进行教学,真正突出学生的主体建构。基于学生的经验进行教学,这是学习建构本质的要求。在理念上,我们都认同经验的重要性,在设计教学活动时也强调让学生在已有经验基础上学习。但在实际教学中,很多教师对学生的经验并没有给予足够的重视,现实的课堂脱离学生实际的现象还非常普遍,这反映出很多教师对经验问题缺少足够的认知。
一、基于学生经验的教学内涵阐述
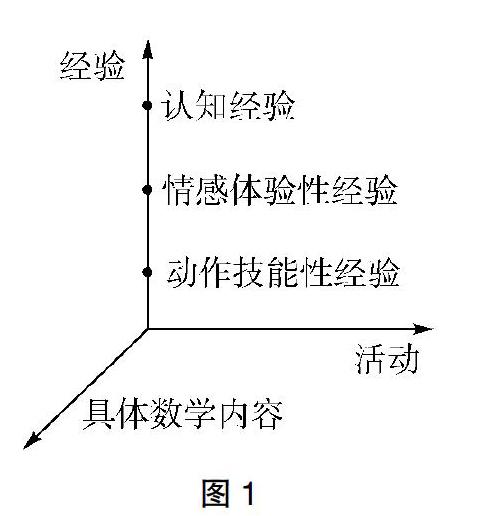
数学教学是学生已有经验与知识交错递进中发展和深化数学思维和数学理解的过程。学生在数学活动中获得的经验,是具体数学内容、活动和经验三个基本因素相互作用下,产生动作技能性经验、情感体现性经验与认知经验等构成的整体,我们可用数学活动经验直观模型图(如图1)加以表征。学生的数学活动经验形式上就是由这三维坐标构成的元素“点”的集合体[2]。
从学生层面来看,在学习之初学生已有三种经验,即原有学习方法的经验、已习得知识的经验和生活的经验。每个学生的生活经验都存在着差异,在学习方法上也会形成个性独特的风格,这些都将不断地内化为他们的学习经验体系,并且这些经验在适当的情境中可以激发出来。学生每学习一个新知识,都将为后续学习积累知识结构上的经验。这些经验通过思维活动、表征活动、同化顺应活动等形成新的认知经验(如图2)。另外,学生的已有经验有三种情况:一是学生已具备的丰富经验,只需要教师加以点拨,就能帮助他们“唤醒”;二是学生有了一定的经验,但还不足以达成学习目标,需要教师“加固”他们的经验;三是学生缺少相应的经验,需要教师提供新的经验或为学生提供获取新经验的机会。一般地,在不同背景下,学生的经验情况会有所不同,应根据不同的目标需求设计活动,并形成新的认知经验结构。
从教师角度来看,分析学生的已有经验是教学设计的第一步,只有充分了解学生的经验,才能有针对性地安排教学活动。在设计和组织教学时,教师应充分考虑学生已具备哪些经验,这些经验处于何种状态等,以便找到学生进一步学习的“最近发展区”,让新知的学习能更好地纳入学生原有的认知结构中。因此,教师要以学生经验为起点,设计合理的活动,为学生提供更多的机会进行观察、实验、思考、内化、反思等。笔者以2019年人教A版高中数学必修第一册“函数y=Asin(ωx+φ)”教学为例,对基于学生经验的数学教学进行研究。
二、教学设计
(一)对接经验,创设情境
情境1:苏州金鸡湖摩天轮。
提出问题:摩天轮在转动过程中,每个座舱距离地面的高度与时间存在什么样的函数关系?
情境2:如图3,筒车是中国古代发明的一种灌溉工具,它省时、省力、环保、经济,现代农村还在大量使用。明朝科学家徐光启在《农政全书》用图4描绘了人们利用筒车的圆周运动进行灌溉的工作原理。
设计意图:教师运用身边的生活情境和数学史料,引导学生与已有的生活经验对接,进入情境的表征活动中,让学生自然而然地产生认知需求,在熟悉的情境中激发生活经验,产生认知驱动力。
(二)运用经验,抽象模型
为了更好地研究问题,教师将情境1和情境2中的问题改编为以下数学问题。
如图5,假设筒车的直径是10m,筒车距离水面最高的高度为8m,该筒车匀速转动一圈需3min。那么,你能用一个合适的函数模型来刻画筒车上某一个盛水筒P距离水面高度H随时间t(min)的关系吗?
问题1:如何研究这个问题?
教师引导学生建立合适的直角坐标系(如图6),将实际问题数学化。
活动:请根据数据写出问题中的数学模型y=5sin(120t+φ)+3,其中φ表示刚开始转动时的初始角,它与选取的初始位置有关。
问题2:上述函数表达式为何不加绝对值?
该问题的提出旨在让学生认识到,这里的“高度”其实类似于之前他们学习正负数时的“海拔”一样也有正负之分。
设计意图:该教学环节是运用已有的基本活动经验进行新的建构活动,即通过建立直角坐标系将实际问题进行数学建模活动,进而抽象出函数模型,为学生进一步的学习打好基础。教师要唤醒学生大脑中已具备的认知经验,让学生在已有经验下进行熟悉的认知活动,这样才可能让学生进行自主建构。
(三)借鉴经验,启发思考
将上述模型一般化后得到本节课要学习的函数模型:y=Asin(ωx+φ)。
问题3:如何研究函数y=Asin(ωx+φ)中A,ω,φ对该函数图象的影响?
问题4:在之前的学习中,我们用怎样的经验来研究类似的问题呢?
教师引导学生回忆初中研究的二次函数y=x2与y=a(x-h)2+k(a≠0)的关系,采用从特殊到一般和控制变量的方法进行研究(如图7)。
不妨先研究φ对图象的影响。为了便于研究,我们可以取特殊的φ值(如φ=π6)进行研究,研究路线如下(如图8)。
问题5:根据上面的探究,你能归纳出φ对函数y=sin(x+φ)图象的影响的一般化结论吗?
教师引导学生进行讨论研究后,用课件出示以下内容。
一般地,当动点P的起始位置P0对应的角为φ时,对应的函数为y=sin(x+φ)(φ≠0),将正弦曲线上所有的点向左(φ>0)或向右(φ<0)平移φ个长度单位就得到y=sin(x+φ)的图象。
设计意图:借鉴之前学习二次函数的活动经验来认识参数φ对y=sin(x+φ)(φ≠0)图象的影响,让学生经历从特殊到一般,再从一般到特殊的思维过程。思维走向是从某个(些)点的变化到所有点的变化规律,再到整个图象的变化规律,从而将特殊的φ对图象的影响规律推广到一般的φ对图象影响的规律。这个过程既包含已有认知经验的再运用,又有新的认知经验的再运用,加强了认知经验在大脑中的重构,使得活动经验更加丰富。
(四)强化经验,形成新知
问题6:你能借助上面探究的过程来研究ω(ω>0)对y=sin(ωx+φ)图象的影响吗?
问题7:根据上面的探究,你能归纳出参数ω对函数y=sin(ωx+φ)图象的影响的一般化结论吗?
问题8:你能用学得的经验研究参数A对y=Asin(ωx+φ)图象的影响吗?
问题9:根据上面的探究,你能归纳出参数A对函数y=Asin(ωx+φ)图象的影响的一般化结论吗?
问题10:通过对这节课的学习,谈谈我们用什么方法研究函数y=Asin(ωx+φ)的图象?你学到了什么研究经验?
课后探究:你还能重新选择A,ω,φ的研究顺序来探究它们对y=Asin(ωx+φ)图象的影响吗?
设计意图:问题6~问题9是相同经验下的同构认知活动,是认知的同化与顺应活动,而且这样的过程还可以延展到课后进一步探究,这对建构学生完整、逻辑连贯的认知过程非常有必要。
三、反思认识
(一)找准经验起点,整体把握内容
数学知识点不是孤立存在的,任何新知都是基于旧知生成,找准新知与旧知的关联点,让学生在似曾相识中对旧知进行回顾,对新知进行建构,主动实现旧知与新知的逻辑关联。因此,准确把握学生的经验起点是实施基于学生经验的教学前提,教师应努力找准知识起点,用好经验起点,激活学生思维。在本节课之前,学生已经学习了正弦函数、余弦函数、正切函数等基本函数的概念、性质及图象等,这是本节课的知识起点;学生已经掌握了研究函数的“基本套路”(从现实生活中抽象出函数模型→对函数模型进行定义→研究函数模型的性质与图象→应用函数模型解决问题),这是本节课的经验起点;也逐步感悟到认识对象的过程都是从具体到复杂的过程(即从初等基本函数到复杂函数),这是本节课的思维起点。之前的认知线路是以“刻画周期性现象的函数模型”这一核心任务展开的(如图9)。[3]而且学生从初中到学习本节课的内容之前,学会了用已学的初等基本函数的经验范式去研究更为复杂的函数,然后又从复杂函数“退化”到简单函数,这样从简单到复杂,再从复杂到简单的双向认知过程是认识函数主要的活动经验。
从这个角度看,基于学生经验的教学体现了单元教学的特質,将单元中具有相同或相似活动过程作为“经验单元”不断地重复激活,运用相同或类似经验进行系统的认知活动,让单元知识在已有活动经验的指引下不断地同化、调整、丰富或重构,最终形成稳定牢固的知识结构留在大脑中。这样的认知过程体现了经验的整体性和单元教学的逻辑连贯性。
(二)实现承上启下,促进自主建构
研究表明,学生是基于已有知识去建构和理解新知识的,每一个新经验都有过往经验的成分,同时也会影响和改变后续经验[4]。因此,在教学时,教师既要考虑到此次活动经验的起点是什么,还要考虑到此次活动为后续学习留下哪些有价值的活动经验,这就是经验的承上启下。本节课中,在研究参数对图象影响的探究方式上,借鉴研究函数y=a(x-h)2+k图象的变化规律与y=x2图象产生联系的经验,自然迁移到将函数y=Asin(ωx+φ)的图象与函数y=sinx的图象产生同化与顺应。在具体研究参数对图象的影响时,既考虑到初中已学二次函数的活动经验[如参数a对y=a(x-h)2+k图象开口大小的影响],又考虑到当前活动经验对后面学习其他参数时所起的思维示范作用。换言之,只要将参数φ这一探究活动讲到位,学生就可以在研究其他参数时进行自主建构。一般情形下,经验具有一定的连续性和可复制性。在设计活动时,教师要运用经验的连续性和可复制性引导学生进行相似的建构与理解,让学生在一定思维范式的引领下进行经验的对接和思维的联结,实现自主建构。
(三)重构原有经验,实现认知提升
如果在教学中不去关注学生的原有经验(有些可能是不好的或不恰当的经验),那么原有经验和新知识的学习就可能发生冲突,对新知识的建构就会形成阻碍。教师在教学中关注学生原有经验,引导他们去体会和认识原有经验中出现偏差或错误的原因,不仅能很好地建构新知识,而且还能使原有不完整或错误的经验成为促进学习的积极因素。比如本节课在研究参数φ对图象的影响时,学生很可能受初中“左加右减”口诀的影响,这种口诀式的“经验”是非理性的,也是肤浅和机械的。只有引导学生分析图象变换的本质才是可靠的,要让他们知道是点的变化才引起图象的变化,点的变换是图象变换的关键,寻找到图象变换前后的对应点,将认知活动的重心聚焦在变换前后对应点的坐标关系上。这样的活动自然成为后面认识其他参数时的先行组织者。数学活动中那些具体数学规律(如本节课中参数对函数影响的规律)的发现要么是被已有认知结构所吸收(同化),要么就是引起已有认知结构的改造(顺应),产生新的认知结构[5]。学生学习新知的过程就是已经获得的经验在新情境中进行检验和迁移的过程,学生的认知结构在这个过程中发生了同化和顺应,逐步实现对原有知识结构的重新组织,即实现了经验的重构。
总之,在实际教学中,教师要充分关注学生的认知经验,设计前后逻辑连贯的数学活动,让学生在活动中进行整体的认知活动,以此促进学生对数学概念的深度理解,真正提升学生的数学核心素养。
参考文献:
[1]江世春.基于学生学习起点的有效教学[J].教学与管理,2013(14):23-24.
[2]仲秀英.学生数学活动经验的内涵探究[J].课程·教材·教法,2010(10):52-56.
[3]丁益民.实施中观教学 促进深度学习[J].数学通讯,2020(20):6-8.
[4]约翰·杜威.我们怎样思维·经验与教育[M].姜文闵,译.北京:人民教育出版社,1991.
[5]刘斌.从构建学生数学认知结构看高中数学教材的编写[J].课程·教材·教法,1998(5):25-28.
(责任编辑:陆顺演)

