具有启动期的Geo/Geo/1/(SWV+MV)离散时间排队模型的稳定性研究
程慧慧,王文娟
(华北水利水电大学,河南 郑州 450046)
0 引言
1970年以来,休假排队系统得到很大的关注[1],且广泛应用于许多领域,比如库存系统、电信网络等.2002年,Servi和Finn[2]提出了一种“半休假策略”,即工作休假策略.与休假策略不同的是,它要求处于工作休假期的服务器不完全停止工作,而是以更低的速率为顾客提供服务.2008年,Li和Tian[3]利用拟生灭过程和矩阵几何解法研究了具有单重工作休假的Geo/Geo/1离散时间排队模型,并进一步求出了模型的随机分解结构.
目前许多文献考虑了休假排队和工作休假排队[4],也有人为了实际需求将启动期加入到排队模型中.2011年,王竟竟[5]研究了具有启动期的Geo/Geo/1/MV离散时间排队模型,并利用矩阵几何解法得到了系统稳定时的平均队长和平均逗留时间.近年来也有少数人研究了两阶段休假策略的排队模型.2017年,Ye和Liu[6]在研究M/M/1连续型排队模型时提出了一种包含单重工作休假和多重休假的新的休假策略(SWV+MV).类比连续型排队模型,Ye和Liu[7]利用矩阵几何解法研究了具有两阶段休假策略的Geo/Geo/1离散时间排队模型,并进一步求出了系统稳定时的平稳分布和随机分解结构(平均队长和平均逗留时间),与此同时建立了连续型与离散型时间排队模型之间的联系.关于Geo/Geo/1离散时间排队模型更多详细的描述可以参考文献[8-10].
本文在Ye和Liu所研究的模型的基础上引入了启动期,并利用矩阵几何解法研究了模型稳定的充要条件和平稳分布,进而研究了模型的随机分解结构、忙循环分析以及数值分析.本文在两种休假策略的基础上引入启动期会使模型的研究更具有实际意义.在现实生活中,两阶段休假策略也得到了很广泛的应用,如果能够在这种休假策略的基础上加入启动期,不仅可以给服务台工作人员提供很多休息时间,还可以起到设备维护保养的作用.
比如在服务中心有两种服务窗口,分别为公司业务服务窗口和个人业务服务窗口.当公司业务窗口的顾客相对较少时,服务中心会保留一个窗口为顾客提供服务,此阶段可以理解为工作休假阶段;若此阶段结束后一直没有顾客接受公司业务窗口的服务而个人业务窗口人数较多时,公司业务窗口全部停止服务并开始为个人业务窗口的顾客提供服务,此阶段可以理解为休假阶段.综上所述,公司业务服务窗口的工作机制可以视为两种休假策略的混合模式.若工作休假结束时公司业务窗口的顾客相对较多而正好是服务人员休息或者机器维修时,那么此阶段可以理解为启动期阶段.
本文的结构如下:第一部分主要是对模型进行了详细描述并得到系统稳定的条件(Markov链的遍历性条件);第二部分通过计算得到系统的平稳分布以及系统稳定时系统的随机分解结构;第三部分是忙循环分析;第四部分是数值分析.
1 模型描述及平衡条件
1.1 模型描述
本文考虑具有启动期和两阶段休假策略的Geo/Geo/1排队模型,关于模型的详细描述如下.
(1) 本文考虑的是晚到的离散时间排队模型.在离散时间排队模型中,顾客的到达、离开和休假的结束都有可能同时发生.为了表达更加明确,假设潜在到达发生在时隙(m-,m)处,其中m-表示在m之前的那一刻.潜在离开发生在(m,m+)处,其中m+表示在m之后的那一刻.
(2) 设系统中顾客到达时间间隔T的概率分布函数为
(3) 服务时间S1和S2的概率分布函数分别为
其中:S1为正规忙期的服务时间;S2为工作休假期的服务时间,μ2<μ1.
(4) 设假期时长V1和V2的概率分布函数分别为
其中:V1为工作休假时长;V2为休假时长.
(5) 启动时间U的概率分布函数为
假设随机变量T、S1、S2、V1、V2、U相互独立.关于模型的工作机制的具体描述如下:
记a—正规忙期,b—工作休假,c—休假,d—启动期.当a结束时系统变空,则进入b阶段;当b结束时,若系统变空进入c阶段,否则进入d阶段;当d结束时进入a阶段;当c结束时,若系统变空再次进入独立同分布的c阶段,否则进入a阶段.
接下来是利用拟生灭链的方法建立Markov链,由此得到系统稳定的条件.
1.2 平衡条件
设Qm表示t=m+处系统中的顾客数,Jm表示t=m+处服务器的状态,即
易知{Qm,Jm}是一个Markov链,其状态空间为
Ω={(0,0),(0,1)}∪{(k,j):k=1,2,…;j=0,1,2,3}.
对任意的实数x∈(0,1),有

转移概率矩阵为
其中:

易知{Qm,Jm}是一个拟生灭链过程.
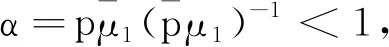
(1)
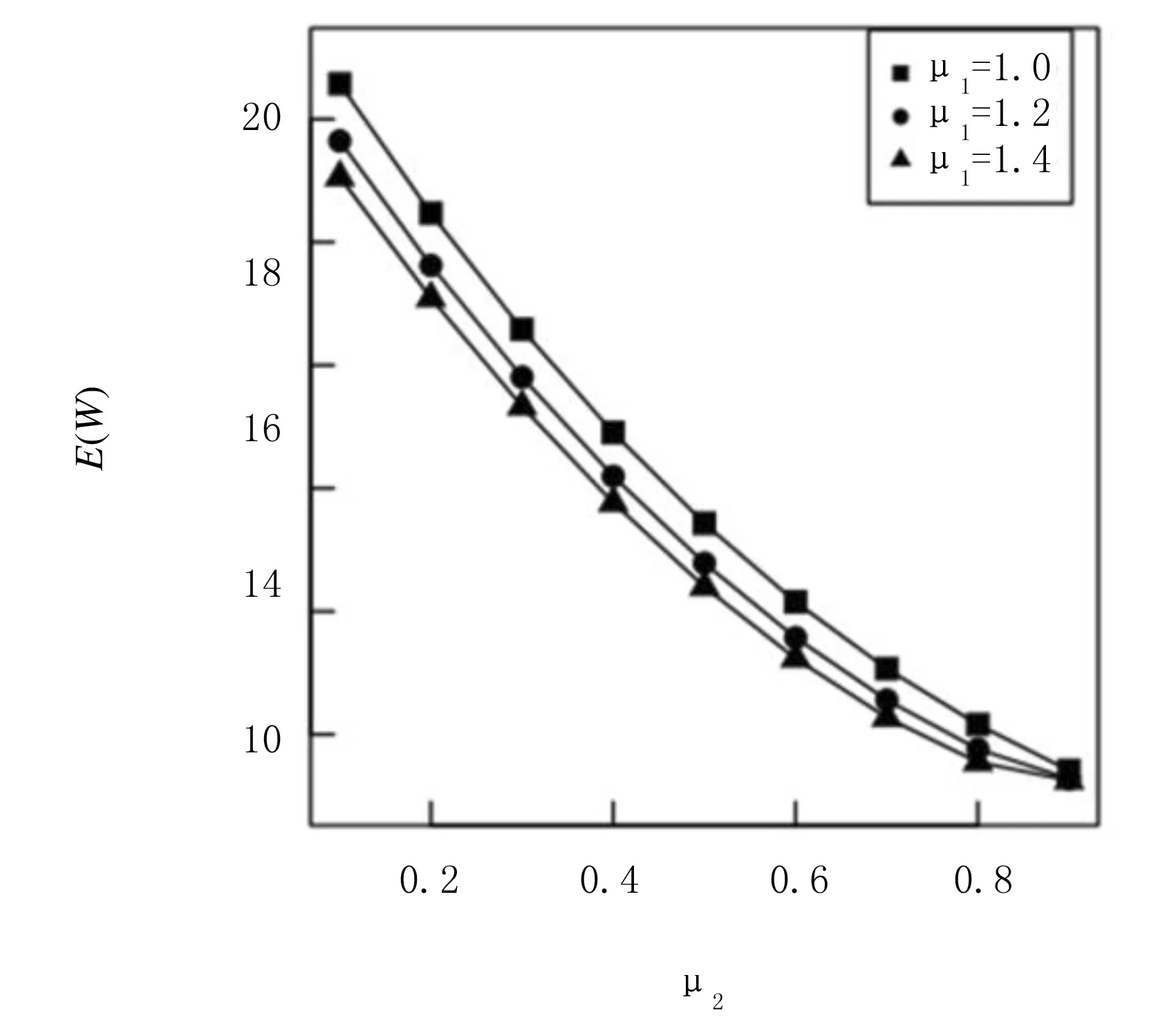
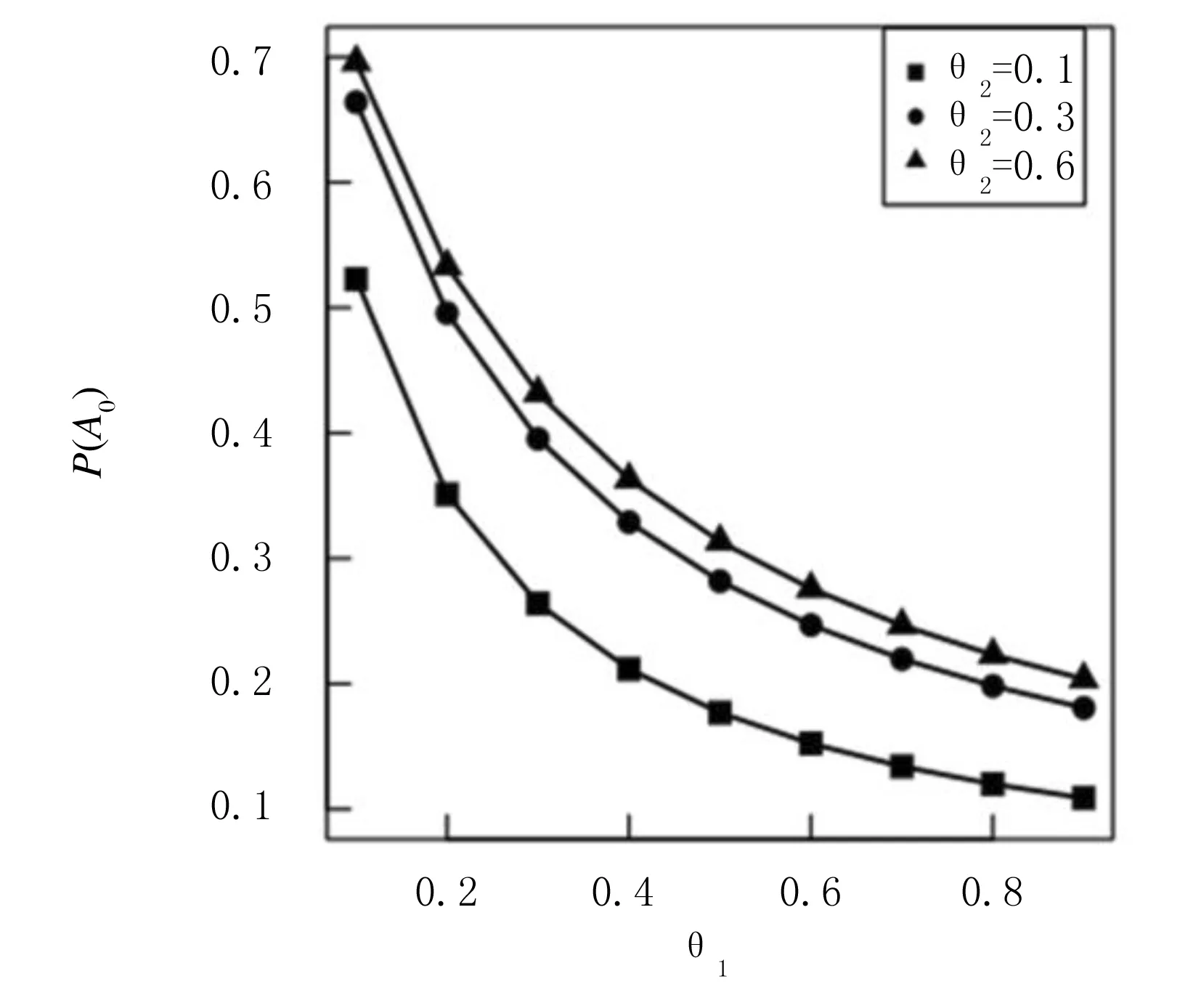
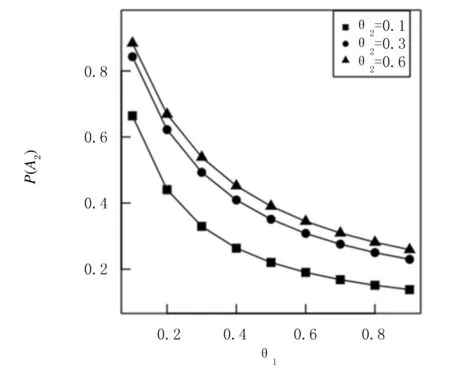
其中0 (2) (3) (4) 证明因为矩阵B0,B1,B2均为上三角矩阵,所以率阵R也为上三角矩阵,即 (5) 把式 (5)代入矩阵方程R=R2B2+RB1+B0,可得 (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) 由 (7) 和 (11) 易得:r12=r23=0.由 (6) 易知二次方程有两个根,一个根为(2) 中的表达式r,另一个根为 (16) 定理2Markov链{Qm,Jm}正常返当且仅当α<1. 证明Markov链{Qm,Jm}正常返当且仅当率阵R的谱半径SP(R)小于1且方程组 (π00,π01,π10,π11,π12)B[R]= (π00,π01,π10,π11,π12) 易知B[R]是一个正则随机矩阵,以B[R]为系数矩阵的方程组有正解.因为r<1且β1<1、β2<1,所以 SP(R)=max(r,α,β1,β2)<1 成立当且仅当α<1.定理得证. 通过定理1和定理2的证明,得到了系统稳定的充要条件,接下来计算系统的平稳分布. 由定理2可知,当α<1时,Markov链{Qm,Jm}正常返,则平稳分布存在. 定义 π0=(π00,π01),πk= (πk0,πk1,πk2,πk3),k=1,2,… 定理3当α<1时,{Qm,Jm}的平稳分布为 (17) 其中: 证明由矩阵几何解法可知 πk=(πk0,πk1,πk2,πk3)= (18) (π00,π01,π10,π11,π12,π13)B[R]= (19) 对式(19)进行展开,得 (20) (21) (22) (23) (24) (25) 通过计算式(20)~(25)可得含有π00的式子,即 由式(1)可得 其中 把(π10,π11,π12,π13)和Rk-1代入式(18)可得含有π00的πk0、πk1、πk2、πk3的表达式,进一步利用归一化条件 可得π00的表达式,将其代入可以得到式 (17).定理得证. 由定理3易知, 本节主要研究的是系统平均队长的随机分解结构. Qd=δ0X0+δ1X1+δ2X2+δ3X3+δ4X4, 其中 证明由方程 (17) 可得系统顾客数Q的概率母函数,即 (26) 其中 又因为 (27) 所以将式(26)代入式(27)可得 (28) 其中 d1= 通过对式(28)计算整理可得 (29) 其中δ0、δ1、δ2、δ3、δ4的表达式见定理4.通过验证易知δ0+δ1+δ2+δ3+δ4=1,故Qd(z)为Qd的概率母函数.定理得证. 由定理4可知其均值为 本节主要研究的是系统平均逗留时间的随机分解结构. 定理5若α<1且μ1>μ2,逗留时间W=W0+Wd,W0为经典无休假排队模型系统稳定时的逗留时间,附加延迟Wd是一个关于随机变量Y0、Y1、Y2、Y3的表达式,即 其中 证明由 (27) 和 (29) 可得 (30) (31) (32) (33) (34) 把(31)~(34)代入 (30) 可得 又因为 所以式 (35) 也可以写成 W(s)=W0(s)Wd(s), 其中经典Geo/Geo/1排队模型逗留时间的概率母函数为 定理得证. 由定理5易知其均值为 本节研究的是系统的其他指标忙循环. 令A0=(Jm=0)、A1=(Jm=1)、A2=(Jm=2)、A3=(Jm=3).假设A3为服务器连续地以服务速率μ1提供服务的时长.由于正规忙期会发生在启动期结束瞬间或休假结束瞬间,故忙循环G由A3、A0、A1和A2构成,即G=A0+A1+A2+A3. (36) 由式(36)可得 (37) 同理可得 (38) (39) (40) 由 (37)、(38)、(39) 和 (40) 易知 E(G)=E(A0)+E(A1)+ E(A2)+E(A3). 本节主要是通过改变某些模型参数来研究其对系统的影响. 例1研究参数μ1和μ2对平均系统大小和平均逗留时间的影响.假设p=0.6,θ1=0.3,θ2=0.4,λ=0.1,当μ1固定时,μ2的变化对平均队长E(Q)和平均逗留时间E(W)的影响的变化趋势如图1和图2所示,都会随着μ2的不断递增而呈现下降的趋势.当固定μ2时,μ1对E(Q)和E(W)有类似的影响.这是因为μ1和μ2的不断递增代表平均服务速率的不断提高,由此导致E(Q)和E(W)的不断递减. 图1 E(Q)随μ2的变化趋势 图2 E(W)随μ2的变化趋势 例2研究参数θ1和θ2分别对P(A0)、P(A1)、P(A2)以及P(A3)的影响.假设p=0.6,μ1=1.6,μ2=0.3,λ=0.1,当固定θ1时,P(A0)和P(A2)的变化曲线如图3~6所示,发现均随着θ2的不断递增而递减,P(A1)和P(A3)均随着θ2的不断递增而递增;但是当固定θ2时,发现θ1对P(A0)、P(A1)、P(A2)以及P(A3)的影响变化趋势恰好与θ2的相反. 图3 P(A0)随θ1的变化趋势 图4 P(A1)随θ1的变化趋势 图5 P(A2)随θ1的变化趋势 图6 P(A3)随θ1的变化趋势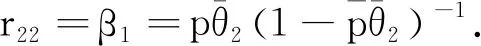
2 系统稳定时的队长分布和随机分解结构
2.1 系统稳定时的队长分布
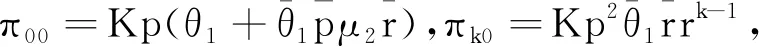
(π10,π11,π12,π13)Rk-1,k≥1,
(π00,π01,π10,π11,π12,π13).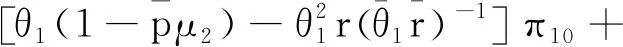

2.2 系统稳定时的平均队长
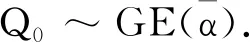
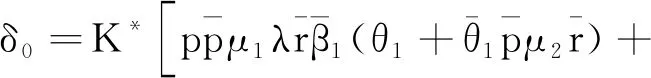
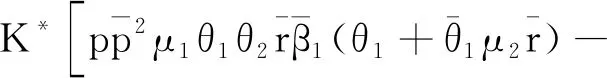


2.3 系统稳定时的平均逗留时间
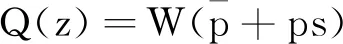

3 忙循环
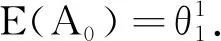
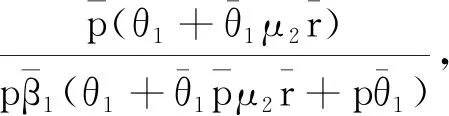

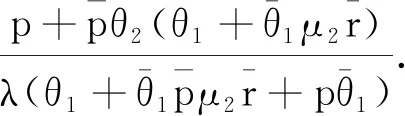
4 数值分析