一类一般随机环境中单边二重随机游动的常返性

张 培

(宿州学院 数学与统计学院,安徽 宿州 234000)

0 引言

M V kozlov[1]在20世纪70年代，首次给出随机环境中的随机游动(简记RWRE)模型.后来Solomon[2]研究了全直线上的RWRE的若干性质.随后诸多概率论工作者研究了随机环境中的随机游动，并且取得许多丰富的结果[3-5].然而随机环境中随机游动的推广——随机环境中的二重随机游动却很少有人研究.随机环境中的二重随机游动是物理学中的一个非常重要的模型，具有较强的实用意义.Toth B和Alili S较为系统地研究了二重随机游动并得到若干结论[6-7]；汪荣明研究随机环境中二重生灭链的马氏性[8]；任敏研究了独立随机环境中单边二重生灭链的常返性[9].本文作者研究了两两不相关随机环境中单边二重生灭链的常返性[10].

本文主要讨论在0点上具有反射壁的一类一般随机环境中单边二重随机游动的常返性，在环境满足一定的条件下给出该模型的正常返和零常返的判别准则.

1 定义与符号

定义1称取值于非负整数集Z+={0,1,2,…}上的随机过程{Xn,n≥0}是随机环境中的单边二重随机游动，若

P(X0=0,X1=1)=1,P(Xn+1=k|X0=0,

X1=1,…,Xn-1=i,Xn=j)=Pij,k，

且

其中

0<βj,αj<1(j≥1),{βj}j≥1，{αj}j≥1

是随机变量序列.

随机变量序列e={βj,αj,j≥0}称为随机环境，其每个现实都称为环境.

因为Xn是不可约的二重马氏链，所以讨论该二重随机游动的常返性，只要讨论在某一点的常返性.不失一般性讨论0点的常返性.

记

2 主要结果及其证明

引理1[2]若对几乎所有的环境{Xn,n≥0}都具有某一性质，则此随机环境中的马氏链{Xn,n≥0}具有此性质.

引理2[8]{Xn,n≥0}为固定环境中的二重随机游动，则

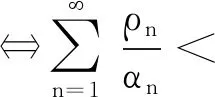
引理3设{ξn,n>0}是方差有界的随机变量序列，且当|i-j|→+∞时,有cov(ξi,ξj)→0成立，则{ξn,n>0}服从大数定律.即对任意的ε>0,有

成立.

证明因为随机变量序列{ξn,n>0}方差有界，所以存在常数M>0，使得

Dξn≤M，

且

对上述ε>0，当n→∞时,有

即{ξn,n>0}服从大数定律[11].

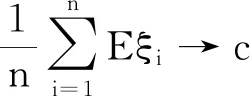
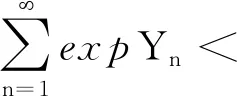
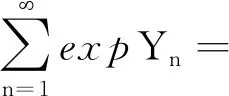
证明因为{ξn,n≥1}是方差有界的随机变量序列，且当|i-j|→+∞时,有cov(ξi,ξj)→0成立，由引理3得{ξn,n≥1}服从大数定律，即对任意的ε>0都有

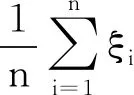
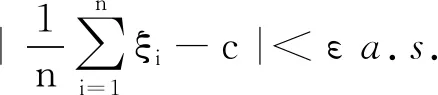
(1)如果c<0时，存在N2∈N+，当n>N2时,有

成立.则有

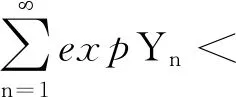
(2)如果c>0，存在N3∈N+，当n>N3时有

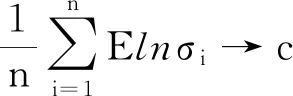
(1)如果c≥0，则{Xn,n≥0}常返；

(2)如果{Xn,n≥0}非常返，则c<0；

(3)如果c>0，则{Xn,n≥0}正常返；

(4)如果c=0，则{Xn,n≥0}零常返.

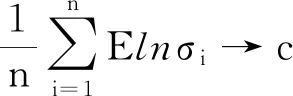
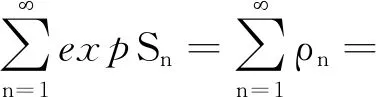
下证结论(3)和结论(4).结合引理3知，如果c>0则有

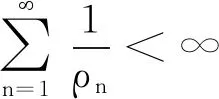
如果c=0，则有

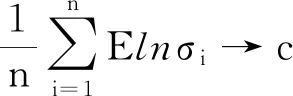
(1)c≥0 ⟺{Xn,n≥0}是常返的；

(2)c<0 ⟺{Xn,n≥0}是非常返的；

(3)c>0 ⟺{Xn,n≥0}是正常返的；

(4)c=0 ⟺{Xn,n≥0}是零常返的.

证明首先证明(1)和(2)的充分性.由定理1(1)可知(1)的充分性成立.

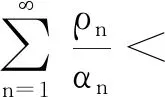
下证必要性，对于(1)若{Xn,n≥0}常返，则必有c≥0，反之如c<0，由(2)的充分性知{Xn,n≥0}非常返，矛盾， 故可得结论(1)的必要性成立.

同理可以证得结论(2)的必要性成立.由定理2的(1)和定理1可知(3)、(4)成立.