巧构基本图形，关注核心素养——2019 年南京市数学中考题第22 题解法赏析

江苏省南京市溧水区东庐初级中学 王 静

一、试题的呈现

二、特色解读

（一）图形简约，内涵丰富

本题呈现方式简约，主要由圆和两条相等的弦（两条弦相交于点P）组成。虽然图形简洁，但考查的内容很丰富，如可用到的知识点：“等角对等边”“全等三角形的判定”“全等三角形对应边（对应角）相等”“在同圆或等圆中，同弧（等弧）所对的圆周角相等”“圆心角、弧、弦三者之间的关系”“垂径定理”“勾股定理”“圆的内接四边形对角互补”“相似的性质与判定”“平行线的性质”“等式的性质”“同角（等角）的补角相等”“三角形内角和定理”“外角的性质”等。考查的能力也很多，如逻辑推理能力、识图能力、构图能力、转化能力、直观想象能力、迁移能力、数学建模能力等。

（二）巧妙构图，关注素养

由于图形本身简约，在解题时需要联想到一些基本图形，如可构造三角形、猫耳朵模型、飞镖模型、“8”字形、“A”字形、圆的内接四边形等，要用到这些基本图形，首先要思考，如何构造这些基本图形，再用构造出来的基本图形解答题目，这正体现了数学的直观想象素养。每一种构图方法，需要严谨的逻辑推理，这也体现了逻辑推理素养。本题图形之所以简洁，是因为其本身是不完整的基本图形，是由基本图形抽出部分元素形成，所以在解答的过程中，需要填补上相应的元素，命题者此种出题方式正是逆用数学抽象的核心素养。添加元素构造基本图形解决问题，更是体现了数学建模素养。由于版面关系，本文只呈现了部分结题思路。

三、解法赏析

（一）利用等角对等边证明线段相等

解法1：构造三角形

如图2，联结BD，因为AB ＝CD，所以＝AB=CD，

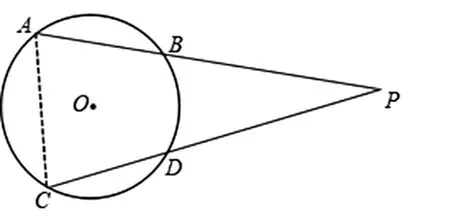
图2

所 以AB+BD ＝CD+CB， 即AD＝CB，

所以∠C ＝∠A，所以PA ＝PC。

解法:2：构造半径和三角形

如 图3， 联 结AC、OA、OB、OC、OD，因为在⊙O 中，所以OA ＝OB=OC=OD，所以∠OAC=∠OCA。

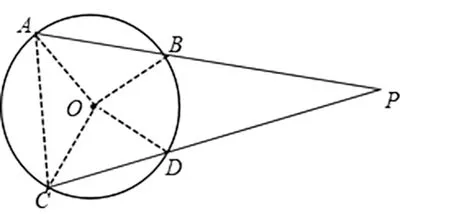
图3

因 为∠OAB+ ∠OBA+ ∠AOB=180°，所以∠OCD+∠ODC+∠COD=180°。

所以2 ∠OAB+∠AOB=180°，2 ∠ OCD+ ∠ COD=1 8 0 °，所 以 ∠OAB= ∠OCD， 所 以∠OAC+∠OAB=∠OCA +∠OCD，所 以∠PAC= ∠PCA， 所 以PA ＝

PC。

解法3：构造同弧（等弧）所对的圆周角

如图4，联结AC、BC、AD，因为BD ＝BD，所以∠PAD ＝ PCB。

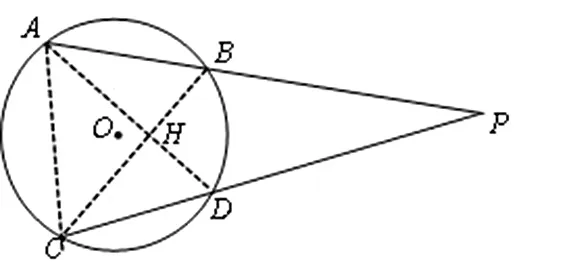
图4

因为AB ＝CD，所以AB ＝CD，所以∠BCA ＝∠DAC。

因为∠PAD ＝∠PCB，∠BCA＝∠DAC， 所 以∠PAD+∠DAC ＝∠PCB+ ∠BCA， 所 以 ∠PAC ＝∠PCA，所以PA=PC。

（二）利用三角形全等证明线段相等

解法4：构造猫耳朵模型

如 图4，联结AC、BC、AD，因为AC ＝AC，所以∠ABC ＝∠CDA。因为AB ＝CD，所以AB ＝CD，所以∠BCA ＝∠DAC，因为在△ABC 与△CDA 中，

∠ABC ＝∠CDA，

∠BCA ＝∠DAC，

AC=CA

所 以△ABC ≌△CDA（AAS），所以∠BAC ＝∠DCA，所以PA=PC。

（三）利用对应线段成比例证明线段相等

解法5:构造横向“A”字形和“8”字形

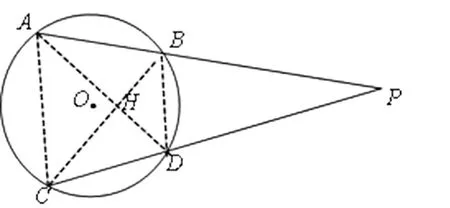
图5

四、教学启示

（一）注重探究过程，积累构图经验

本文的多种不同的解法，涉及到构造“猫耳朵”模型、“飞镖”模型、“8”字形、“A”字形、三角形、圆内接四边形等，这些构造法都很常见。在平时的教学中，课本的例题或是定理的探究过程中，有许多需要“构图”才能解决，如在证明勾股定理逆定理时，需要另外构造一个直角三角形，而有很多教师在讲解勾股定理逆定理时，直接告诉结论，导致很多学生对这种构造法毫不知晓。从本文所探究的中考题，可看出试题重在考查识图、构图能力，这些能力的培养，教师应在日常教学中，一以贯之地落实知识的探究过程，积累一些数学方法、数学模型，才能让这些方法成为解决新题的构图经验。如果教师在平时教学中，注重知识的探究过程，那么这种思维过程，也将成为一种构图经验，成为学生解题时的一种灵感顿悟。

（二）立足基本图形，注重构图过程

基本图形在学业考试考查中主要围绕基本图形的叠加、隐藏的综合应用，解决这类问题的关键是平时要做好基本图形的积累，加强分离、补形、构造的相关训练，掌握解决这类问题的基本策略。“构造”即“构图”，指构造出基本图形，构图过程其实包括四个环节：储图、想图、构图、用图。四个环节相辅相成，缺少任一环节都不能顺利地解决相关习题，但想图、构图的过程是整个构图过程的关键环节。在实际教学中，教师为了节省时间，对于一些必须构图才能解答的习题，没有给学生想图、构图的时间，直接给出构图方法。以致学生碰到类似题型时，仍然不会构图。因此，教师应给学生充足的探究时间，这样经过思考后，即使没有构出图形，等到教师讲解时，也能加深对此题的印象，再遇到同类型的题目时，便能调用头脑中的知识储备，找到解题的突破口。同时在教学中，教师应该向学生介绍为何这样构图。如何想到的，这其实就是要引导学生知道构图的依据是原有的基本图形。每一种构图方法，其实都源于一种基本图形。因此解题教学中，教师应注重构图过程，并启发学生思考这样构图的依据是什么，才能达到“解一题，同一类，会一片”的效果。

（三）注重一图多“构”，关注核心素养

在数学解题过程中，一题多“构”不仅能培养学生的发散思维，而且能培养学生的直观想象能力。《义务教育数学课程标准》（2011 年版）指出：教学活动必须建立在学生认知发展水平和已有经验基础上。由于每个学生的最近发展区不一样，所以不同的构图方法可能适合不同的学生。因此，教师应注重对一道习题采取多种构图方法，不仅有利于调动学生的知识内存，提升学生的综合解题能力，更能促进了学生知识系统结构化。需要构图才能解决的习题，说明原图被抽出了部分元素，这正逆向训练了学生的数学抽象素养。有些构图法在解决某些习题时可能比较烦琐，但是对别的题目，可能是简单的方法。因此，平时教学中注意“一题多构”能加强知识的纵横联系，帮助学生构建合理的知识结构与知识系统，提升学生在新问题情境下准确把握核心知识、形成解题决策的能力。因此，构造多种基本图形解决问题，建立几何模型，实际上更是一种数学建模素养。