吊舱SINS/GNSS组合导航多杆臂效应在线估计算法

翁 浚，刘健宁，寇 科，连天虹，李鹤群，陈学忠

(西安理工大学机械与精密仪器工程学院，西安710048)

机载光学吊舱安装有光电、红外、激光、合成孔径雷达等设备，能够实现飞机对地目标的跟踪监视、地形测绘成像、重点区域巡逻监视和地形规避等功能。随着精确制导武器的不断发展，机载侦察/瞄准吊舱已成为现代战机实施精确打击的重要组成部分。

随着机载光电探测技术的不断进步，对获取光电模块的实时姿态精度要求也不断提高。飞机一般都配有机载惯导设备，其导航精度较高。现有大部分的吊舱可通过转位机构的框架角，将飞机的姿态角转化为光电测量设备的姿态角。激光陀螺捷联惯导系统作为主流的航空惯导设备，具有高动态、抗冲击、高精度等优势，但其陀螺信号去抖所需的高阶数低通滤波器[1-5]及导航信号数据链路的传输[6,7]都不可避免地引入时间延迟问题。且吊舱光学设备与机载惯导必然不会安装在相同位置，机身挠曲变形引入的姿态误差同样不可忽略[8,9]。

由于安装于吊舱内部的子惯导、吊舱和卫星天线的几何中心在空间的安装位置不同，必然存在杆臂误差。子惯导内部三只加速度计间的杆臂误差又称作尺寸效应，可通过转位机构翻转的系统级标定方法获得[10]，补偿尺寸效应后的惯导系统在高动态环境下有着更好的速度精度[11,12]。惯导与卫星天线之间的杆臂误差参数可作为Kalman 滤波参数建模，以在线估计的方式进行补偿[13,14]，亦可以直接测量吊舱中心到卫星天线测量中心的杆臂参数，在滤波器量测处直接减去[11]，引入的速度和定位误差与飞机本身的姿态变化有关。吊舱与子惯导之间的杆臂误差一般提及的较少，距离几厘米到几十厘米不等，其值虽然可能小于吊舱/卫星天线之间的杆臂误差，但其引入的速度和定位误差与吊舱框架角的变化有关。在执行任务期间框架角的变化很可能非常剧烈，如果不对其进行补偿，则必将影响SINS/GNSS 组合导航滤波器的稳定性。本文推导了SINS/GNSS 组合导航算法中相关坐标系的姿态转换关系，考虑了多种杆臂效应的影响，提出了一种适用于吊舱SINS/GNSS 组合导航的多杆臂效应在线估计算法。

1 姿态转换关系

为了精确补偿杆臂效应的影响，需要知道吊舱子惯导、吊舱框架、飞机主惯导（Master Inertial Navigation System, MINS）之间的姿态转换关系。姿态转换将涉及如下几个直角坐标系：

1)子惯导载体坐标系b系：原点ob位于子惯导几何中心处，子惯导与光学仪器一同捷联安装于转位机构的内部台面上；xb轴沿子惯导壳体的右侧；yb轴沿子惯导壳体向前；zb轴沿子惯导壳体向上；

2)吊舱实时坐标系p系：原点op位于吊舱三轴转位机构的几何中心处；xp轴沿吊舱内部安装面的右侧；yp轴沿舱内部安装面向前；zp轴沿舱内部安装面向上；

3)吊舱初始坐标系p0系：当吊舱转位机构3 个框架角为0 时，p0系与p系重合；

4)机翼坐标系a系：坐标系与吊舱/机翼间的安装面固联，原点oa位于安装面上；xa沿安装靠面向右；ya沿安装靠面向前；za沿安装靠面向上；

5) 主惯导坐标系m系：原点om位于飞机主惯导几何中心处，主惯导捷联安装于机舱内部；xm沿主惯导壳体的右侧；ym沿主惯导壳体向前；zm沿主惯导壳体向上；

6) 导航坐标系n系：原点on位于飞机几何中心处；xn沿当地东向（E）；yn沿当地北向（N）；zn沿当地垂线向上（U）。

图1 为吊舱、子惯导、主惯导、卫星天线的空间位置关系几何示意图。由图1 可知：

图1 吊舱SINS/GNSS 组合导航设备空间位置关系几何示意图Fig.1 Geometric diagram of spatial position relationship of pod SINS/GNSS integrated navigation equipment

其中，为子惯导与导航坐标系间的转换矩阵，为同样安装于框架内部台面上的光学仪器提供实时的姿态信息；为吊舱到子惯导的转换矩阵，由于子惯导捷联安装于框架内部安装面上，其为常值矩阵；为飞机到吊舱初始坐标系的转换矩阵，由于吊舱捷联安装于飞机机体上，其为常值矩阵；(t)为主惯导到飞机的转换矩阵，一般主惯导安装于机舱内部，而吊舱安装于机翼下，矩阵实时变化的原因在于随机的机身/机翼挠曲变形角。

为转位机构的实时转动引入的吊舱坐标系转换矩阵，以图1 为例，吊舱初始坐标系p0系到吊舱实时坐标系p系的旋转依次沿y-x-z方向，转动角度为 Θy, Θx,Θz。忽略时间变量t，则：

当然，若实际吊舱的转动次序与图1 不同，可采用类似式(2)的姿态矩阵链乘的形式获得计算公式。

由式(1)很容易得到：

式(4)就是利用主惯导姿态矩阵和实时框架角 Θi(i=x,y,z)近似计算子惯导姿态矩阵(t)的公式。由于挠曲变形、主惯导信息传输延迟、安装角标定不准确等因素的影响，直接使用式(4)计算得到的姿态信息很难保证其准确性，不过可以作为组合导航开始时刻子惯导的姿态初值。

2 杆臂效应

吊舱SINS/GNSS 组合导航系统中存在多组杆臂效应的影响，下面分别进行描述。

（1）加速度计组件的尺寸效应

如图2 所示，由于每支加速度计的测量中心与子惯导惯性测量单元的中心ob必然存在杆臂效应，一般称作加速度计组件的尺寸效应。其引入的加速度计输出测量误差：

加速度计组件的尺寸效应误差属于惯性测量单元的内部参数，可以在实验室通过专门的标定试验获得[16]，该误差理应在产品出厂前做好标定补偿工作。

图2 加速度计组件尺寸效应的空间示意图Fig. 2 Spatial diagram of the size effect of the accelerometer component

（2）吊舱内杆臂

如图1 所示，子惯导中心ob与吊舱中心op间的内杆臂为bp→L，两中心点间的位置差异

其中，pSINS,pPOD分别为子惯导和吊舱中心点位置；L,λ,h分别为当地的纬度、经度和高度； RM,RN分别为当地子午圈、卯酉圈半径；为内杆臂在子惯导坐标系下的投影，由于子惯导与吊舱安装面为刚性连接，为常值向量；为导航系下的位置偏差到纬度、经度、高度偏差的转换矩阵。

随着吊舱框架角的转动，内杆臂还会使得子惯导与吊舱中心导航系下的速度存在差异，其值为：

其中，时间间隔Δtk=tk-tk-1应尽量小，使得更新频率1/Δtk能覆盖吊舱转动的环境带宽。

（3）飞机外杆臂

如图1 所示，吊舱中心op与卫星天线测量中心oG间的外杆臂为Lp→G，两中心点间的位置差异：

随着飞机的转动，外杆臂还会使得吊舱与卫星天线测量中心的速度存在差异，其值为：

当然，类似尺寸效应的补偿方式，如果能够直接测量得到内、外杆臂的值，则可以直接通过式(6)(8)(9)(10)进行补偿。考虑组合导航算法的通用性，及杆臂直接测量的难度较大，下面提出一种能够在线补偿内、外杆臂的吊舱SINS/GNSS 组合导航滤波器设计。

3 吊舱SINS/GNSS 组合滤波器设计

为了实时估计补偿内、外杆臂的影响，设计的滤波器状态如下，

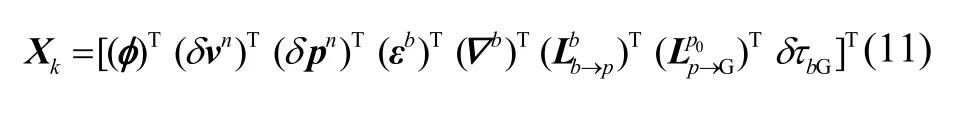
状态转移矩阵：

其中，矩阵“0m×n”表示m行n列的零矩阵。

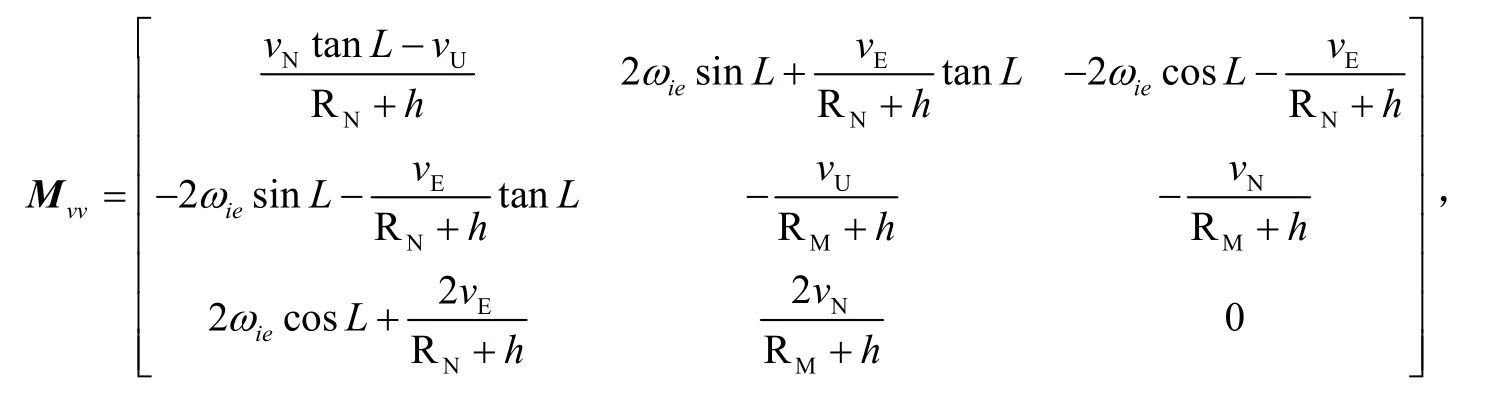
τg,τa为陀螺仪、加速度计的相关时间常数。

GNSS 接收机计算得到导航信息用于构建卡尔曼滤波器的量测信息，参考3 节中的杆臂效应及SINS/GNSS 时间不同步的影响，k时刻的位置量测：

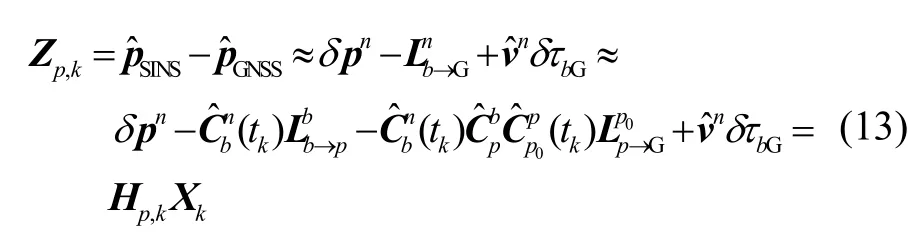
其中，位置量测矩阵：

k时刻的速度量测：

其中，速度量测矩阵：

式(11)～(16)构成了考虑杆臂效应与时间延迟影响的适用于吊舱的SINS/GNSS 组合导航滤波器。

4 飞行试验与数据分析

吊舱组合导航系统的性能验证试验在某固定翼飞机上进行，飞机主惯导为高精度激光陀螺惯性导航系统，航向精度优于0.06 °。GNSS 卫星接收机、吊舱框架角信息直接通过串口总线发给子惯导，主惯导信息则需要通过主控设备数据打包处理后，再通过航空总线转发给子惯导，存在一定的时间延迟。吊舱内安装有数据记录仪以存储所有导航相关的离线数据。子惯导采用0.3 °/h 的低精度光纤陀螺，100 μg的挠性加速度计作为惯性元件，GNSS 采用北斗/GPS 双频单天线接收机，定位精度15 m，速度精度0.1 m/s。

某次飞行试验的数据如图3-5 所示。

图3 飞行速度及轨迹Fig.3 Flight speed and trajectory

由图3 可知，本次飞行的机动较为丰富，包含：上升、下降、转弯、巡航等，飞行高度大于3000 m，飞行速度可达220 km/h。

从图4 中主惯导的姿态角变化可以看出，飞机的横滚和俯仰角度变化相对较小，主要为飞机转弯机动引起的航向角变化。吊舱框架角的变化比飞机姿态角更为剧烈，转动主要集中在吊舱的x,y两个轴向。

图4 吊舱框架角与主惯导姿态角Fig.4 Pod frame angle and main inertial navigation attitude angle

由图5 可知，正是由于飞机和吊舱框架的角度变化频繁，吊舱内子惯导的陀螺仪输出的最大角速度可达到100 °/s，加速度计三个轴向的输出都可达到1g量级。假设杆臂长度为0.1 m，若不对其进行补偿， 转动引入的速度误差可达到100 ° /s ×0.1m ≈0.17m/s ，大于GNSS 的速度精度。

图5 吊舱惯导系统的陀螺仪与加速度计输出Fig. 5 Gyroscope and accelerometer output of the pod inertial navigation system

为了验证组合导航的姿态角精度，对式(4)简单移项并结合实时的吊舱框架角，可将计算得到的实时子惯导姿态转换为主惯导姿态。

如图6 所示，实线为子惯导结合吊舱框架角计算得到的飞机姿态，虚线为主惯导输出的飞机姿态，两者的姿态角曲线十分接近，证明转换公式的准确性。

图6 组合导航姿态角对比Fig.6 Integrated navigation attitude angle contrast

为了使主惯导的姿态信息能够作为子惯导的真实姿态参考，应当尽量减小飞机挠曲变形、时间延迟的影响。参考飞行速度和框架角曲线，选取飞机近似直线飞行且框架角变化平缓的点，取点间隔大约5～10 min。作为对比，设计了16 维卡尔曼滤波器，滤波状态与式(11)类似且包含时间延迟误差，但不考虑内、外杆臂参数。两种滤波算法的姿态误差如图7 所示。

图7 组合导航的姿态误差Fig.7 Attitude error of integrated navigation

可以看出，在线估计了内、外杆臂的滤波器，其姿态误差波动要明显较小。经计算，在线估计杆臂的姿态角误差均方差为：东向0.0363 °，北向0.0599 °，天向0.0771 °；未估计杆臂的姿态角误差均方差为：东向0.0822 °，北向0.0566 °，天向0.2079 °，与传统组合导航算法相比，本文提出的算法航向精度提高了1 倍。

图8 为内、外杆臂的在线估计结果。上图为外杆臂在线估计曲线，下图为内杆臂在线估计曲线。可以看出在3000 s 附近，随着飞机和吊舱框架转动的充分，内、外杆臂的估计曲线已收敛到稳态值。外杆臂没有事先测量，但考虑到实际飞行时GNSS天线安装位置与吊舱中心十分接近，估计结果基本符合实际情况。内杆臂最终的估计结果为x方向-12 mm，y方向119 mm，z方向20 mm。通过结构设计的图纸上直接测量得到的内杆臂值为x方向0 mm，y方向125 mm，z方向10 mm，两者间误差仅在1 cm 左右。

图8 内、外杆臂的在线估计结果Fig.8 Online estimation results of the inner outer level-arms

5 结 论

由于吊舱在执行任务过程中，吊舱框架与飞机都可能产生频繁机动，多种杆臂效应的存在影响了实际系统的量测精度，进而降低了组合导航的姿态精度。本文推导了吊舱SINS/GNSS 组合导航系统中有关坐标系的姿态转换关系，分析了杆臂效应的影响，并在此基础上提出了一种适用于吊舱的SINS/GNSS 组合导航滤波器。飞行试验证明了本文提出的滤波算法能够准确在线估计出组合导航系统的杆臂值，相比传统滤波算法姿态精度有明显提高，航向精度较传统组合导航算法提高了1 倍，具有一定的工程应用价值。