基于改进麻雀搜索算法的无人机集群置信传播协同定位方法

熊 智，李欣童，熊 骏，陈明星，刘建业

(1. 南京航空航天大学自动化学院导航研究中心，南京 211106； 2. 先进飞行器导航、控制与健康管理工业和信息化部重点实验室，南京 211106)

近年来，无人机飞行任务已经从单一无人机向集群无人机的方向发展，无人机集群通过信息的相互合作与传输，执行多个无人机的特殊编队任务[1]。它不是简单意义上“量”的增加，而是在智能上有“质”的突破，具备在复杂动态环境下能实现大规模自主性的集群协同效应的能力，有着任务分散化、分布式智能化、去中心自主化等潜在价值。

无人机任务执行中需要高精度定位信息，在近距离编队飞行系统中，无人机需要准确、实时的定位信息来进行避碰、任务调度和精确控制[2][3]。受成本与无人机机载的约束，只有少量无人机能携带高性能传感器[4]。针对大规模集群无人机的定位精度问题，国内外学者对协同定位算法进行了探究。与传统的仅依赖单个无人机传感器的多源融合方法相比，协同定位充分利用了协同网络中所有节点之间的几何关系和所有机载传感器的观测数据[5,6]。文献[7]针对非线性模型，设计了一种动态非参数置信传播算法获得无人机位置信息，但计算量较大，只对二维空间进行了仿真，不适合大规模集群无人机使用。文献[8]提出了一种基于相对位置估计和置信传播的协同定位框架。利用消息传递算法的优势结合卡尔曼滤波，实现低成本近距无人机编队协同定位。

实时性是集群无人机协同定位的一项技术痛点，网络中存在大量过剩冗余的协同信息，对定位精度贡献度不高，导致计算负荷大且无法满足精度及实时性需求。如何对节点的协同信息进行筛选，找到稳定可靠的信源无人机是集群无人机中需要解决的难题。集群的协同精度不仅与自身的传感器设备有关，还与飞行构型有关，构型的优劣可以用几何精度因子（GDOP）量化，GDOP 越小，对集群定位就越有利。文献[9]分析了节点数量和传感器精度对无线传感器网络定位精度的影响，提出了定位精度下限的计算方法。文献[10]使用无人车辅助无人机的导航，无人车位置设计用于减少无人车和无人机之间的GDOP，仿真结果显示大幅降低了无人机的定位误差。因此对集群无人机导航中的信源节点进行筛选，可以简化协同定位算法的过程。麻雀搜索算法（Sparrow Search Algortihm, SSA）是2020 年由shen 提出的一种最新的群智优化算法，比传统的优化算法具有精度高，稳定性好等特点[11]，常用于处理非线性复杂系统的优化问题，适用于集群编队这类实时性要求高的应用场景。将SSA 算法应用到信源无人机的筛选中，利用GDOP作为筛选标准，可以选择出最优的组合方式。因此研究基于SSA 优化的无人机集群协同定位方法，从而提高导航系统性能，具有重要的研究意义。

本文提出了一种基于改进SSA 的无人机集群置信传播（Belief Propagation, BP）协同定位方法，利用BP 框架不断进行信息更新推断，在无人机进行信息交互时，提出了以GDOP 值为适应度函数的改进SSA，寻优得到最优几何构型，与该最优构型中的无人机进行信息交互，从而实现了对低贡献度信息的排除和筛选，在确保精度的基础上减少计算量，最终仿真验证本方法的有效性。

1 集群无人机置信传播协同定位方法

假设有N架无人机，无人机i从0 时刻到t时刻的所有状态信息量观测量包括卫星和相邻无人机的相对测距信息。假设具有一阶马尔可夫性，即根据贝叶斯定理，预测和更新过程为

式(1)为预测过程，t时刻之前所有观测量式(2)为更新过程，通过t时刻获得的最新观测信息按照式(2)更新。初始化条件为因此可得后验概率分布为

通过式(3)构建因子图，进而采用置信传播算法求解。无人机群定位问题通过因子图模型的形式进行建模，即可求得任一节点的状态，协同定位问题即为计算t时刻前机载导航信息和观测信息的后验概率分布，即位置置信度(Positional Belief, PB)：

根据集群协同定位的特征，将与变量有关的因子分为预测因子和修正因子。其中修正因子包含两类：自身观测信息,iselfz和与邻节点相互观测信息(j属于i节点的一个邻节点)。由此建立无人机集群协同定位过程的因子图模型[12]。如图1 为BP 图模型推理。

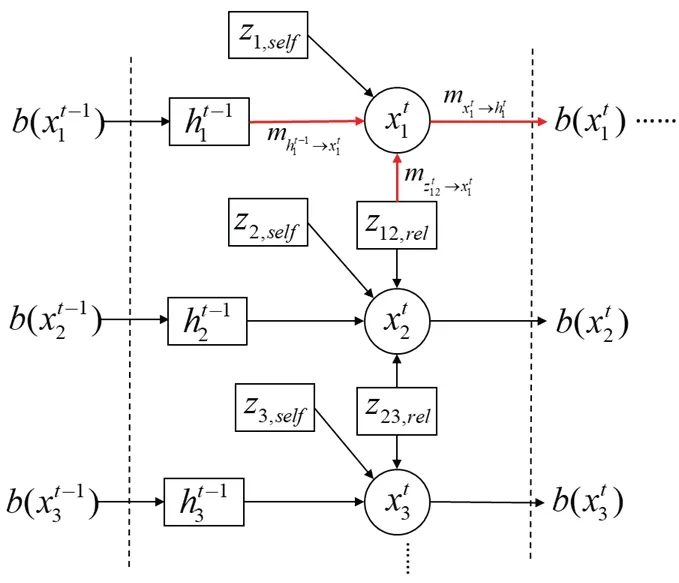
图1 编队无人机协同定位因子图Fig.1 FG of swarm UAVs localization system

结合集群无人机的实际情况，给出下列合理假设：

① 所有无人机的初始位置信息和状态信息更

新过程是相互独立：

③ 无人机自身的观测信息在不同时刻相互独立的，且只和无人机当前时刻以及前一时刻的状态有关：

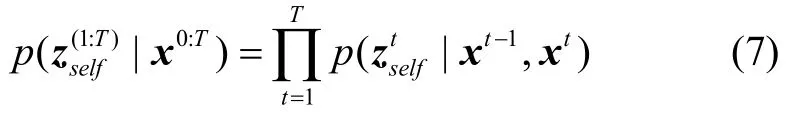
④ 第i架无人机的自身观测量只和它自身的状态量有关，即不同无人机之间的自身观测量是相互独立的；并且相邻无人机之间的相对观测信息是条件独立的：

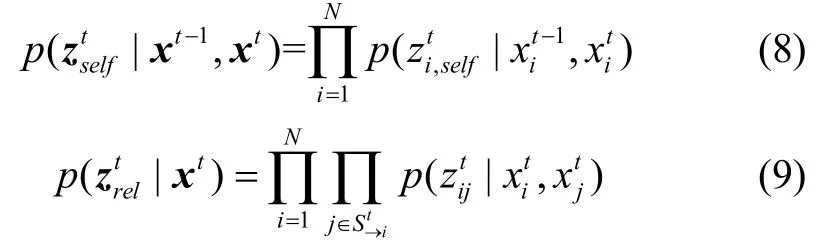
基于以上假设，结合式(3)任一时刻协同网络中后验概率分布可分解为式(10)[8]。

结合图1 和式(10)可以进一步进行因式分解，最终对BP 进行最小均方误差估计，具体算法执行步骤将在2.5 节详述。由式(11)和式(12)可以看出，协同信息和BP 的连续乘积带来了大量计算负荷，而节点i流入的协同信息越多，对状态节点也会有着更好的估计效果。但协同信息越多，相应的计算量就越大，因此需要排除低贡献度信息，对协同信息进行筛选，简化协同定位算法的过程，本文提出了一种改进的麻雀搜索算法平衡计算量与精度的问题。

2 改进的麻雀搜索算法

2.1 麻雀搜索算法

SSA 算法模拟麻雀寻找食物的过程就是寻优的过程，其种群表示如下：

其中，S为麻雀种群矩阵，sF为适应度值矩阵，ns代表第n只麻雀，即指代第n种无人机的组合方式，为麻雀算法中一只麻雀的一维数组，d是变量的维数，为第n只麻雀的适应度值，即第n种组合方式的GDOP 值。计算每一只麻雀适应度if，选出当前最优值bf和其对应的无人机组合方式以及当前最劣的适应度值wf和其对应无人机组合方式

麻雀觅食过程可定义为发现者-加入者模型，并加入警戒者机制。按照各自的规则进行迭代，位置更新方程分别如下:

其中iter为迭代次数，为第j个麻雀在第k维的无人机编号，α和Q为随机数，L是一个一行多维的全一矩阵，R2∈[0,1]和ST∈[0.5,1]分别为预警值和安全值。当预警值小于安全值时搜索环境安全，发现者可广泛搜索，带领种群获得更高的适应度值；当预警值大于安全值表示麻雀遇到了捕食者，迅速调整策略飞向安全区。

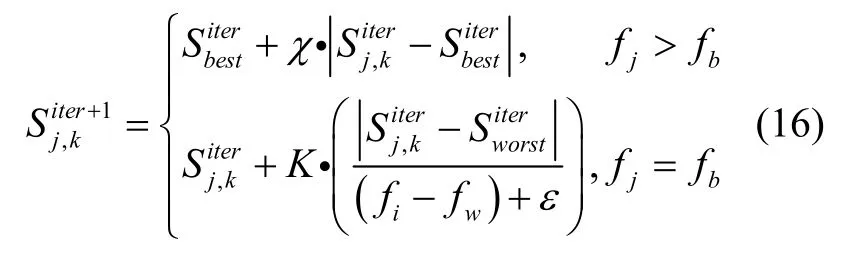
χ和K为随机数；当fj＞fb为警戒者位于种群边缘，处于危险状态；fj=fb为警戒者处于种群中间意识到危险，需要趋向其他麻雀群。

2.2 适应度函数

本文假设测距误差为零均值高斯分布，无人机集群保持时钟同步，测距值如下形式：

上标e表示地心地固ECEF 坐标系，对式(17)进行泰勒展开并保留一阶项，得到可拓展如下形式：

Hi为方向余弦矩阵，载体位置偏差的误差协方差为，σ2为测距误差的方差，GDOP就被定义为的迹的平方根。

2.3 改进麻雀搜索算法

标准的麻雀搜索算法中，因为大多数智能算法的初始值都由随机数产生，会使数值远离最优值，影响最终效果；并且种群会在中后期无法跳出局部最优，本章采取混沌初始化和自适应t 分布变异两种改进方式，避免传统麻雀搜索算法陷入局部最优，提高搜索能力。

2.3.1 混沌初始化

混沌是指在确定性动力学系统中表现出的不可预测的、类似随机性的运动，具有随机性、规律性、在一定范围内不重复遍历等特点。Tent Map混沌模型为经典的混沌模型，其Tent 映射表达式如下：

其中Gk+1、Gk为k+1 和k时刻的状态值，为映射参数。如图2 所示，蓝色圆圈和红色星号分别代表了混沌模型和随机数产生的初值结果。随机数在椭圆框中取值集中，而在矩形框中基本没有取值，因此采用Tent Map 混沌模型代替随机数初始化，不仅保持种群的多样性和覆盖性，而且使得算法脱离局部最优值，有更强的全局搜索能力[13]。本文利用混沌初始化模型更新发现者、追随者、警戒者。

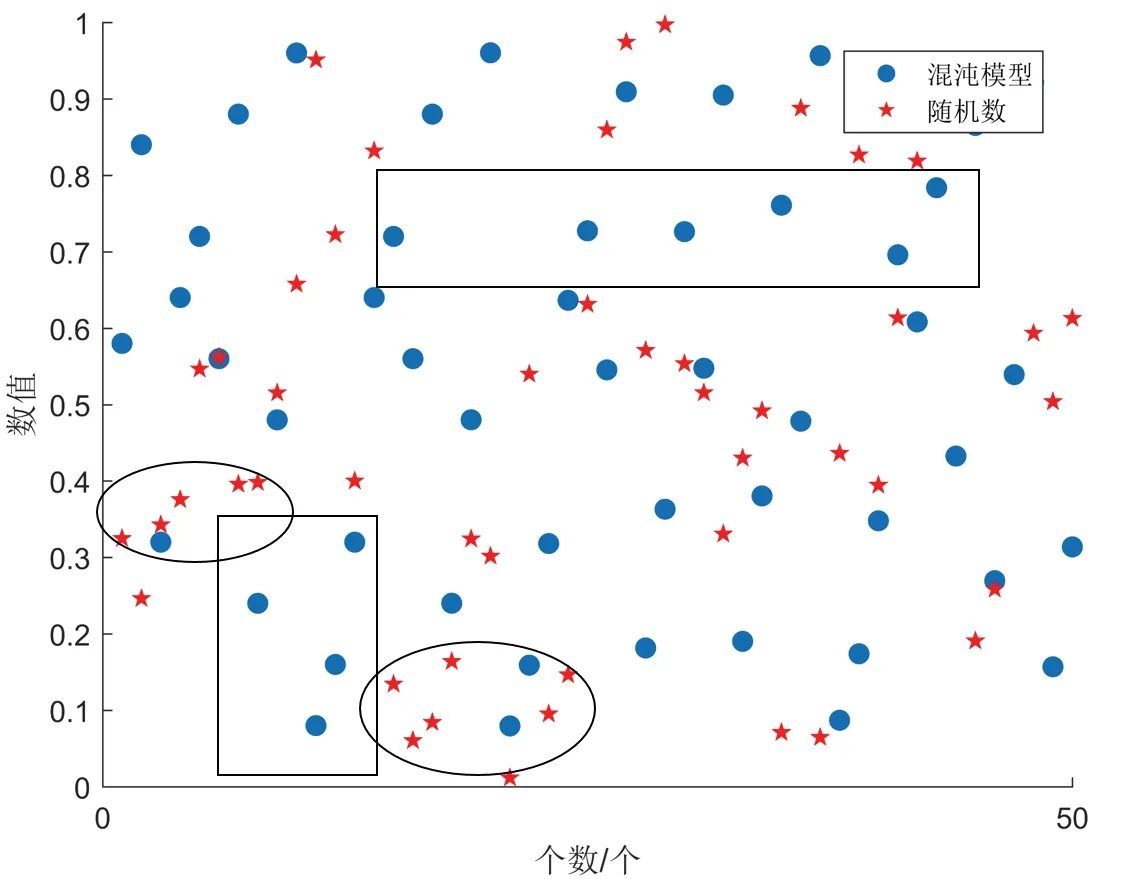
图2 混沌模型与随机数初始化对比Fig.2 Comparison of chaos model and random number initialization

2.3.2 自适应t 分布变异

设定变异阈值，当小于阈值时，进行自适应t 分布变异，定义如下：

2.4 算法步骤

综上所述，基于改进SSA 的BP 无人机集群协同定位算法流程如图3 所示。

图3 算法流程图Fig.3 Flowchart of algorithms

步骤1：初始化所有节点的位置，混沌初始化SSA算法；

步骤5：回到步骤3 进行迭代，确保高精度位置信息通过BP 送达到集群中每架无人机，直到位置置信度收敛；

步骤6：对后验位置信息，即位置PB 求均值得到对应无人机状态信息的最小均方误差估计，且成为下一时刻t+1 时刻的信息初始值。

3 仿真分析

3.1 仿真条件设置

设置如下仿真环境：以搭载高精度传感器的长机为中心，100 m 范围内随机生成30 架僚机，如图4(a)所示。长机僚机飞行轨迹如图4(b)所示。所有无人机搭载测距范围为60 m 的UWB 模块，考虑无人机轴距及荷载等原因，将相邻无人机之间的安全距离设为6 m，每一架僚机选择与相邻五架无人机信息协同信息的交互。表1 为无人机机载传感器参数配置，量测噪声均设置为高斯噪声。

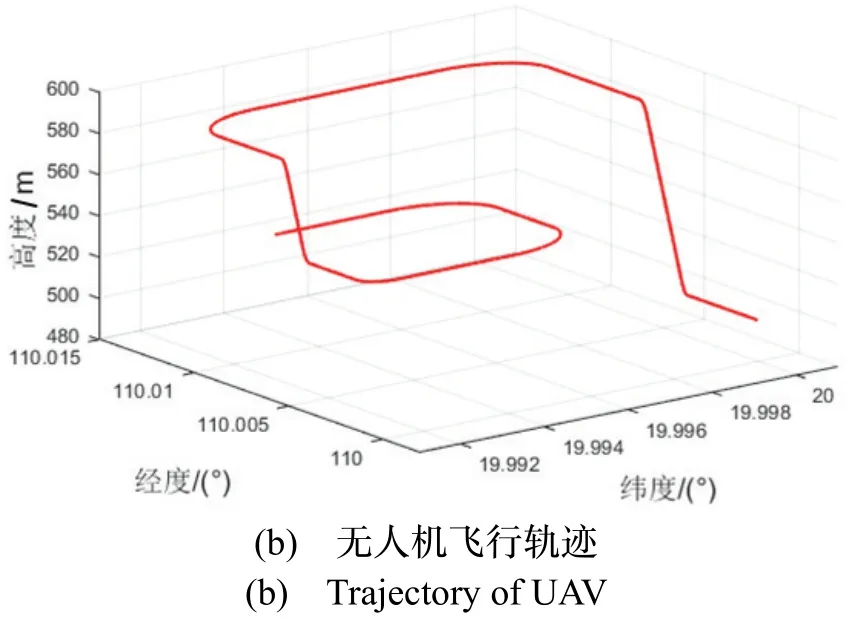
图4 仿真场景和飞行轨迹Fig.4 Simulation scenario and trajectory

表1 传感器参数配置Tab.1 Sensor parameters configuration

3.2 仿真结果与分析

首先探究改进麻雀搜索算法性能。种群规模设为N= 20，迭代次数为200，发现者个数和警戒者麻雀个数均取种群规模的20%。选择某时刻无人机i的GDOP，并与原始粒子群算法、原始麻雀搜索算法和改进粒子群算法适应度值进行对比，适应度值对比曲线结果如图5 所示。

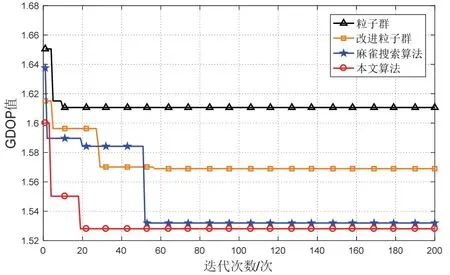
图5 算法收敛曲线Fig.5 Algorithm convergence curve

图中经典算法粒子群和改进粒子群算法过早陷入了局部最优解，原始麻雀搜索算法在55 次迭代后收敛精度优于前两种算法。本文的改进麻雀搜索算法收敛速度和收敛精度优于任何对比算法。

采用本文的改进SSA 优化的BP 算法，随机选取集群系统中两架僚机进行定位精度的分析，图6 给出了如下所示的三种不同算法下僚机在地球坐标系下三个坐标方向上的定位误差对比曲线。

① 本文算法：本文提出的改进麻雀搜索算法优化的置信传播无人机集群协同定位算法；

② BP 协同：文献[8]中提出的协同导航方法；

③ 无协同：僚机采用低精度的INS/GPS 系统进行松组合导航，长僚机之间不进行信息交互。

图6 表明，低性能僚机采用本文算法协同定位方法，极大提高了僚机的定位误差精度，误差曲线明显优于其余两种对比方法。并且进一步对三种算法僚机的定位误差精度进行定量的分析，对该无人机定位均方根误差(RMSE)和精确率（Accuracy）进行了统计，精确率定义为结果如表2 所示。

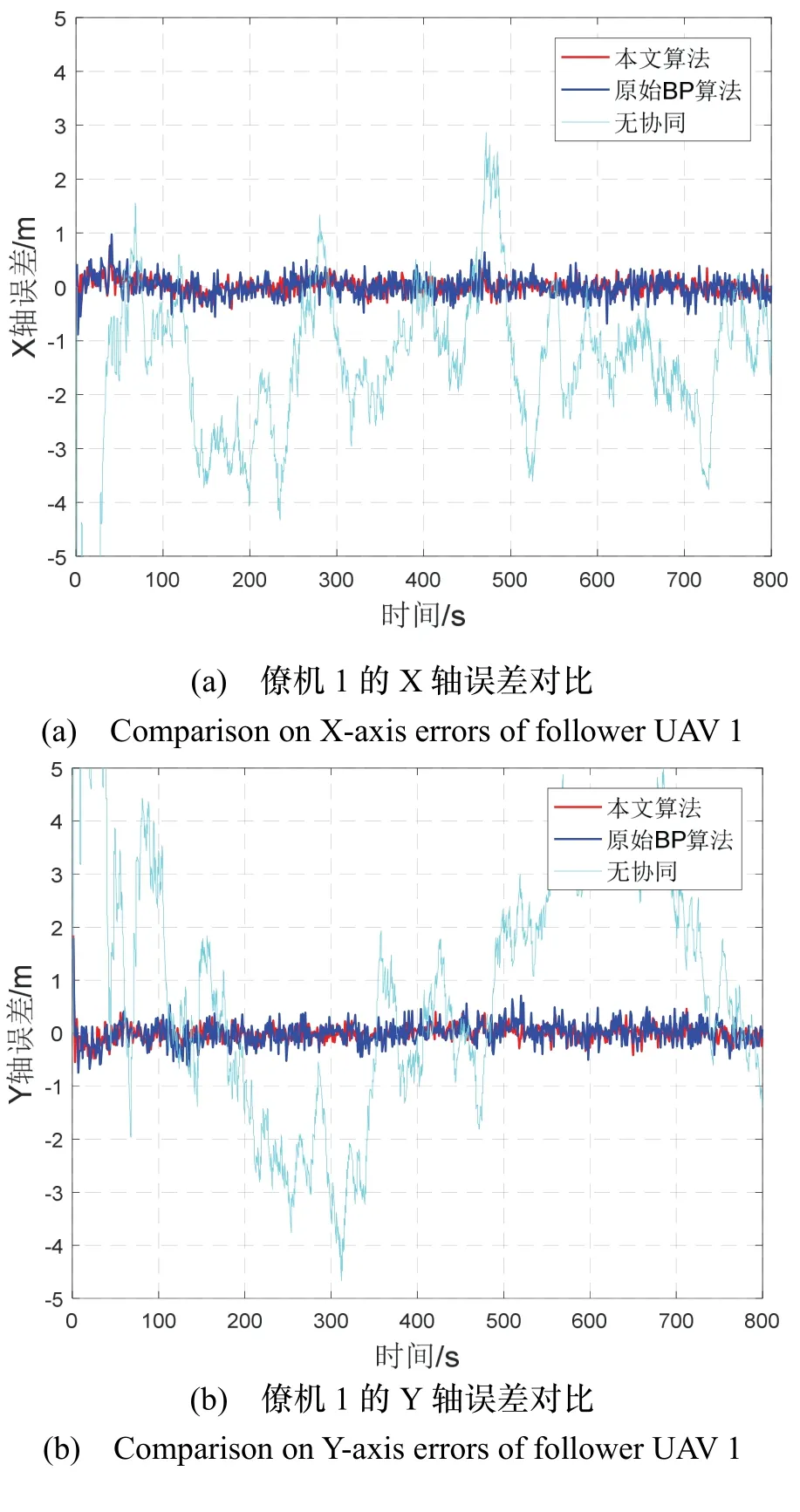
根据图6 和表2 所示的结果，本文算法具有较小的RMSE 误差和较精确的估计精度，与原始BP 算法相比，估计更加稳定和准确。根据定义中的可以推断出经过改进SSA 算法优化后，最优的GDOP值使得协同信息提高了对僚机定位的贡献度。

图6 定位误差对比曲线Fig.6 Comparison on position errors

表2 定位误差统计结果Tab.2 Statistics of position error

为了将提出的协同定位框架与其他框架进行比较，无人机定位估计误差的计算公式如式(23)所示。

为了体现集群中僚机的整体表现，采用误差累积分布函数(CDF)，对比不同方法编队飞行中的所有僚机的定位误差。如图7 显示了累积分布三种方法的CDF，并与长机进行比较。

由图7 可以看出，本文所提出的方法的定位精度是最为接近长机定位精度的，并且优于原始BP 算法。例如，集群中无协同定位只有0.3%的定位误差小于0.5 m，但本文所提出的方法可将该比例提高到97.1%，略低于高精度长机（98.9%），高于原始BP（81.9%）。

图7 定位误差累积分布比较Fig.7 CDF comparison of positioning errors

本文算法对定位估计精度进行了优化，针对本文方法的复杂度进行进一步的分析。对上述方法的算法效率进行了对比，并设置了对照组：随机选择五条协同信息CM，与本文算法进行精度上和效率上的对比。利用Matlab 的‘tic’和‘toc’函数获得记录每个周期代码的运行时间，用来表示算法框架的计算负载。结果如图8 所示。

图8 定位误差与处理时间对比Fig.8 Comparison of positioning error and processing time

图8 表示，本文算法计算负载远小于原始BP 算法，每个周期的时间提升为原始BP 的2.8 倍。与对照组相比在计算量上二者较为近似，在定位精度上优于对照组，验证了本文方法的有效性，简化了协同定位算法过程的计算复杂度，提升了僚机的整体导航性能。

4 结 论

针对无人机集群协同导航的问题，本文提出利用改进SSA 算法优化的BP 算法，对基本的麻雀搜索算法进行混沌初始化和自适应变异改进，增加探索能力和种群多样性，并验证了收敛性和精度。并且研究了基于因子图的集群无人机编队协同定位模型，将无人机定位问题转化为求解后验概率分布问题。仿真结果表明，改进的麻雀搜索算法收敛速度和精度优于所有对比算法。本文协同定位框架能够提升集群中整体僚机定位精度，优于原始BP 算法，既解决了计算量大的问题，又提高了协同导航性能，在保证精度的基础上简化了计算量，且不依赖高精度传感器，降低了成本，实现了无人机集群的高精度实时协同定位。