旋转导向钻井工具姿态测量陀螺仪故障估计与处理方法

耿艳峰，孙 建，王伟亮，程民彪

（中国石油大学(华东)控制科学与工程学院，青岛 266580）

旋转导向钻井技术是20 世纪90 年代发展起来的一项自动化钻井技术[1]。与传统的滑动导向钻井相比，旋转导向钻井工具的井眼净化效果好，井身轨迹控制精度高，位移延伸能力强[1,2]。工具面角参数是导向钻井工具中的一项重要的姿态参数，表征了钻头的钻进方向，实现工具面角的准确可靠测量是提高旋转导向钻井工具性能的前提。常用的工具面角测量传感器包括：加速度计、磁通门、陀螺仪。大量研究表明单一传感器往往难以实现准确测量[3-5]，通过融合不同传感器数据可以显著提高测量精度，互补滤波和自适应卡尔曼滤波[6,7]两种数据融合方法的应用较为常见。钻井过程噪声复杂，既有钻具轴向、周向以及扭转振动产生的周期性噪声、又有随着钻井深度、压力增加的趋势性噪声，噪声分布往往是未知的。考虑到钻井过程参数范围基本可以确定，将非周期性噪声、模型线性化、陀螺仪漂移等影响因素视为幅值有界但分布未知误差(unknown but bounded error, UBB)进行处理具有理论上的可行性。针对UBB 误差的集员估计理论近年来得到了快速发展，文献[8]利用基于椭球集合的扩展集员卡尔曼滤波算法实现车辆位置和速度估计；文献[9]提出一种基于中心对称多胞体的集员状态估计算法实现一类包含未知输入和系统干扰系统的状态估计；文献[10]提出一种基于观测器误差界分区估计的集员估计方法，实现一类包含未知但有界干扰和噪声的广义系统的状态估计。

高温、高压、强振动的钻井环境极易导致工具面角传感器出现故障，进一步可能引发其它事故。如果故障无法在井下进行处理，就要进行起钻维修，严重影响了导向钻井技术的推广应用。文献[11]中详细分析了旋转导向稳定平台可能发生的故障类型，并针对不同传感器提出了相应的故障检测与处理方法，基本解决了加速度计的故障处理问题，但对于陀螺仪故障缺少相应的故障诊断和处理方法。实际系统中，故障的幅值信息是后续处理的重要基础，能够提供幅值信息的故障估计问题得到越来越多的学者关注。文献[12]使用无迹卡尔曼滤波器对故障参数进行估计，实现故障发生后对控制器进行重构；文献[13]在考虑模型不确定性以及环境噪声的条件下，基于H∞理论利用线性矩阵不等式设计非线性观测器研究了一类非线性系统的故障检测、隔离和估计方法；文献[14]提出一种新的滑模观测器实现不满足常见故障估计条件的系统的故障估计。

基于上述分析，本文尝试利用自适应扩展集员卡尔曼滤波(adaptive set-membership extended Kalman filtering, ASM-EKF)算法解决导向钻井工具面角传感器的故障估计与处理问题。将陀螺仪故障项增广为状态变量，利用加速度计建立测量方程来估计陀螺仪故障，并对陀螺仪输出进行校正，实现陀螺仪故障条件下工具面角的可靠测量。最后通过模拟样机测试与仿真验证方案的有效性，为故障条件下工具面角的精确测量与控制系统的正常运行奠定基础。

1 工具面角测量系统滤波动态模型

1.1 工具面角测量方案

以动态指向式旋转导向钻井工具为例，其工具面角的传感器布局方案参见文献[7]，如图1 所示。采用双加速度计和陀螺仪实现组合测量，双加速度计对称布局消除运动加速度的影响，消除运动加速度后的各轴加速度测量值用αx，αy，αz表示，加速度计的x轴平行于稳定平台轴线，y轴指向稳定平台切线，z轴指向稳定平台轴心。

图1 稳定平台传感器示意图Fig.1 The diagram of stabilized platform sensors

则工具面角可由式(1)计算：

陀螺仪敏感轴与稳定平台轴向平行，用来测量稳定平台对地转速，陀螺仪测量工具面角的公式为：

其中：φk是k时刻的工具面角，ωk为k时刻的陀螺仪输出转速，Ts为采样时间。

1.2 工具面角组合测量模型

考虑陀螺仪输出发生加性故障，根据式(2)获得校正后的工具面角的迭代形式如下：

其中：fk表示陀螺仪的加性故障。

将工具面角和陀螺仪故障作为系统状态，陀螺仪输出作为系统输入，建立如下的状态方程：

根据式(1)建立双加速度计量测方程，结合式(4)的状态方程，建立工具面角测量系统的状态空间模型：

2 自适应扩展集员卡尔曼滤波器

2.1 扩展集员卡尔曼滤波算法

扩展集员卡尔曼滤波算法是在卡尔曼滤波框架下，引入未知但有界误差项来提升算法估计性能。扩展卡尔曼滤波算法需要对非线性模型线性化，将线性化误差看作未知但有界误差项描述为椭球集合，并与模型中涉及的未知但有界误差求取闵可夫斯基和(Minkowski sum)，获得新的未知但有界误差项[8,15]。模型(5)的量测方程为非线性方程，线性化造成的未知但有界误差项描述为。

对量测方程线性化，将式(5)变换为如下形式：

具有未知但有界误差项和随机误差项的非线性系统的最优卡尔曼滤波增益、一步预测协方差以及新息协方差计算公式如下[8]：

2.2 UBB 误差的数学描述

由式(5)可知，状态方程是线性方程，不存在线性化误差。因此，状态方程的未知但有界误差考虑陀螺仪的漂移以及模型误差，将描述为如下椭球集合：

量测方程存在线性化误差，将线性化误差作为未知但有界误差项考虑到滤波算法中，用来描述。量测方程的线性化过程如下：

陀螺仪具有多种故障形式，当发生突变故障时，新息协方差矩阵Pk会突然增加，导致滤波模型中的测量UBB 误差增大，进而影响滤波算法收敛速度，甚至导致发散。在滤波过程趋于稳态值后，新息矩阵趋于极小值，可以根据新息矩阵的大小来判断是否需要调节预测值，此处引入如下评价指标：

式中：ke为测量误差矩阵，表示新息协方差矩阵的F范数，为测量误差矩阵的2 范数，γ根据实际工况进行选取，γ值越大，故障估计的快速性越好，滤波算法的稳定性越差。

取nr=1，采用外边界椭球来描述拉格朗日余项，同时保证正定，将进行如下描述：

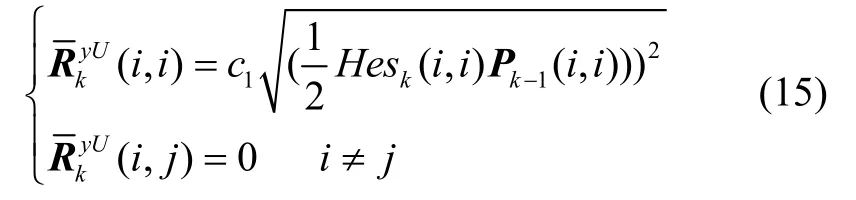
其中：Hesk表示量测方程的Hessian矩阵，c1∈(0,1]为调节因子，若式(14)满足，则认为滤波状态稳定，c1=1 ；否则根据实际工况在取值范围内选取。

2.3 集员Sage-Husa 自适应滤波算法

井下工况复杂多变，导向工具钻进的过程中，地质的变化、稳定平台运动状态的变化、振动强度的变化等情况，都会导致系统噪声和测量噪声的变化，Sage-Husa 自适应滤波算法可以不断地调整系统模型参数和噪声模型统计参数，使滤波性能达到最优，常规的 Sage-Husa 算法都是针对传统卡尔曼滤波模型[16,17]，下面基于集员卡尔曼框架对该算法进行改进。

结合集员卡尔曼滤波框架以及式(7)的数学模型可得：

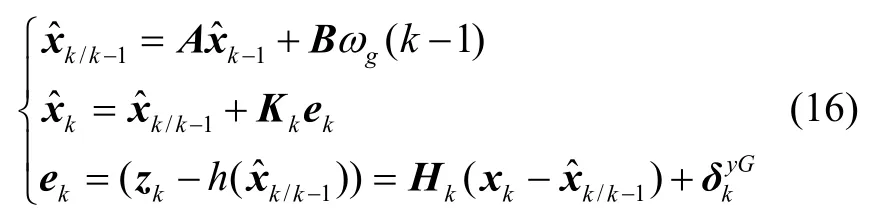
由式(7)和式(16)可得：

对式(17)左右同乘对应转置，求取数学期望可得：

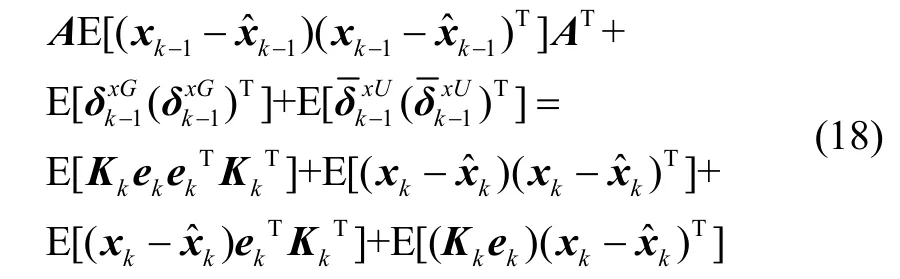
对式(18)等式右边项进行处理：

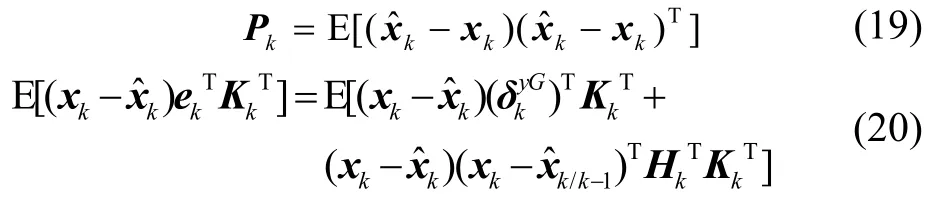
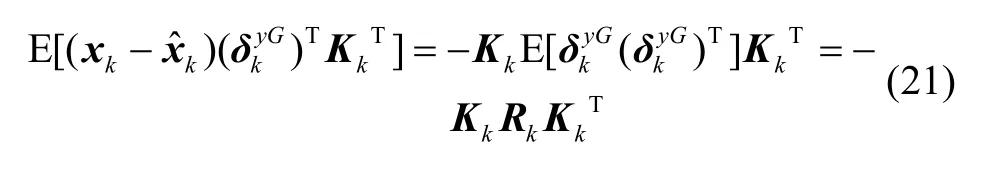
由式(9)(18)结合式(19)～(22)变换，Qk-1替换为Qk得：

根据式(16)可得：

故测量噪声Rk的自适应算法为：

为提升算法快速性，提出如下自适应方案：

综上所述，自适应扩展集员卡尔曼滤波算法的具体步骤如下：

步骤2：根据式(14)、式(15)更新测量UBB 误差；

步骤4：根据式(8)更新最优卡尔曼增益Kk；

步骤5：根据式(9)更新一步预测协方差Pk/k-1；

步骤6：根据式(10)更新协方差阵Pk；

步骤7：根据式(26)更新过程噪声Qk和测量噪声Rk

3 仿真与实验

粘滑运动是钻进过程中常见的工况，频率在0.05～0.5 Hz 之间[18]，根据稳定平台测控系统性能要求，在0.5 Hz，200%粘滑度的工况下，工具面角波动范围应小于15 °[11]，这对算法的跟踪性能提出了较高的要求。为了测试更严苛的条件，考虑井斜角为90 °的情况；使用0.5 Hz，波动幅值20 °的正弦模拟粘滑工况进行测试。

3.1 典型钻井工况仿真

假设导向钻井工具工作在造斜工况，工具面角固定在183 °；30 s 后发生粘滑，工具面角在183 °基准上以频率为0.5 Hz，幅值为20 °的正弦波动；60 s 后改成稳斜钻进，工具面角以36 ° /s的速度在0～360 °范围内线性变化，90 s 后继续造斜，工具面角维持在183 °持续到120 s。Baker Hughes 是世界三大油服公司之一，其井下振动手册[19]将钻具振动分为7 个等级，其中处于良好安全运行环境下的钻具振动级别为0 级[0, 0.5 g)以及1 级[0.5 g,1 g)，因此本文选取加速度计的振动噪声方差为0.5g2，模拟1 级钻具振动条件下的加速度计信号输出情况；参考陀螺仪手册[20]，陀螺仪的速率噪声密度为陀螺仪噪声带宽设置为1600 Hz，故将陀螺仪测量噪声方差设置为100( ° /s)2，模拟陀螺仪固有噪声。

为验证ASM-EKF 性能以及陀螺仪故障估计性能，分别在如表1 所示三种陀螺仪故障状态下进行仿真。采用双加速度计测量方案、陀螺仪测量方案以及自适应扩展集员卡尔曼滤波算法来对上述工况以及故障类型下的工具面角的进行解算。

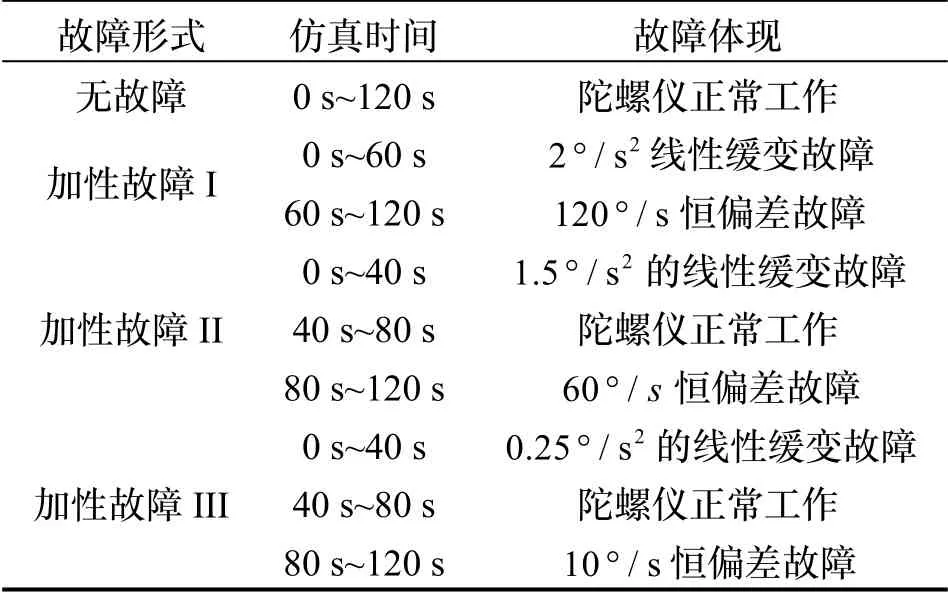
表1 仿真故障类型Tab.1 Simulation fault type

图2 是无故障情况下三种方案的处理效果，加速度计解算受噪声影响非常剧烈，解算工具面角的RMSE 为50.52 °，无法反映实际工具面角；陀螺仪解算相对精确，但陀螺仪解算工具面角值存在0.1 /s° 的漂移，120 s 后存在13.74 °的解算误差，难以满足性能要求；ASM-EKF 算法则利用数据融合的优势，精准地实现了对工具面角的估计，RMSE 为2.55 °。图3展示了加性故障I 下的解算效果，陀螺仪由于故障原因失去解算能力，ASM-EKF 算法仍然能够精确的进行工具面角估计，RMSE 为2.49 °，并且准确地估计出陀螺仪的故障。

图2 无故障仿真效果Fig.2 Fault-free simulation effect

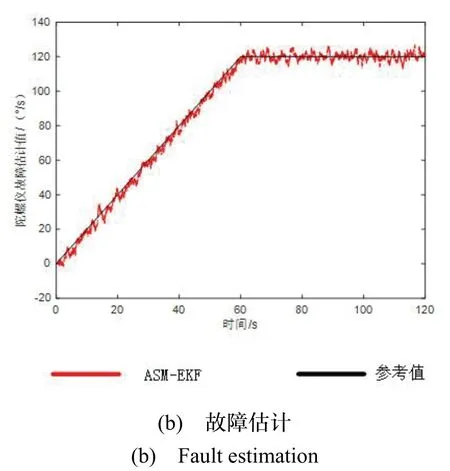
图3 加性故障I 仿真效果Fig.3 Additive fault I simulation effect

图4 展示了加性故障II 下的解算效果，突变故障下，ASM-EKF 算法的工具面角估计值有短暂的偏离，但是很快调整到实际值附近波动，RMSE 为3.57 °，故障估计值很快跟踪上突变故障。

图4 加性故障II 仿真效果Fig.4 Additive fault II simulation effect

图5 展示了加性故障III 下的解算效果，验证了ASM-EKF 算法对于10 °/s 范围内故障下的工具面角仍具有较好的估计效果，RMSE 为2.55 °，与无故障时的精度相当。陀螺仪的故障估计值可以反映故障变化趋势，但是相对于故障幅值具有较大的波动，这是由于陀螺仪固有噪声与故障幅值处于同一量级所致。此时故障已在陀螺噪声范围内，严格意义地讲，其已不能按故障进行处理。综上说明ASM-EKF 算法具有大幅值陀螺仪加性故障的快速跟踪估计能力，可以实现多种复杂加性故障下工具面角的可靠测量。

图5 加性故障III 仿真效果 Fig.5 Additive fault III simulation effect

3.2 模拟样机实测结果

课题组自行开发的动态指向式旋转导向钻井工具原理样机参见图6，样机采用两组三轴重力加速度计MMA8451 以及一个单轴陀螺仪ADXRS645 测量工具面角。

图6 原理样机结构图Fig.6 Principle prototype structure drawing

利用原理样机测试导向钻井工具四种工作状态来验证该算法的实用性，同时分别与文献[7]中采用的自适应扩展卡尔曼 (adaptive extended Kalman filtering,AEKF) 算法以及文献[8]中提出的集员卡尔曼(set-membership extended Kalman filtering, SM-EKF)算法进行对比，验证本文算法的性能。

实验模拟的四种典型工况：恒工具面角、粘滑工况、稳斜工况、调工具面角。实验中将原理样机固定在振动台上模拟井下振动。振动台开启后，振动频率由0Hz 过渡到50Hz，之后持续在50Hz 振动，振动频率的变化能够更好地模拟井下实际振动，同时增加了处理的复杂性。

陀螺仪故障主要针对持续故障以及突变故障两种情况进行模拟，具体故障模拟形式如表2 所示。

表2 实验故障类型Tab.2 Experimental fault type

利用上述三种算法获得的工具面角估计值与陀螺仪故障估计值如图7、8 所示。不同故障条件下，不同算法获得的工具面角估计值与参考值的均方根误差(RMSE)对比如表3 所示。噪声方差以及未知但有界误差方差的初始值设置为[8]：

表3 工具面角估计均方根误差Tab.3 Root mean square error of toolface estimation

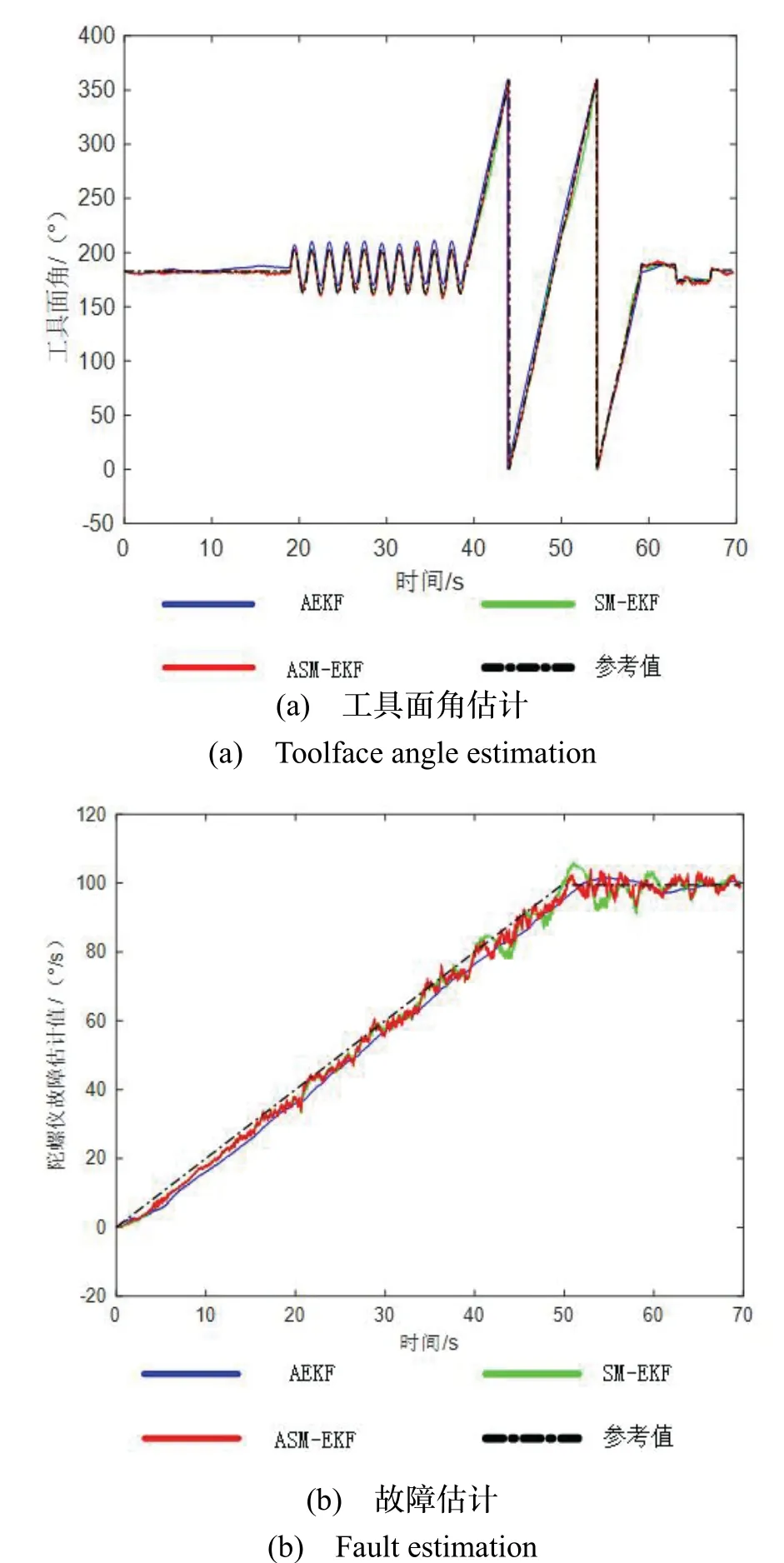
图7 加性故障I 实测效果Fig.7 Additive fault I measurement effect

从图7、图8 中可以看出，对于加性故障I，三种算法都可以实现故障的跟踪估计，文献[7]所采用的AEKF 算法始终存在一定的偏离，导致工具面角的估计也存在一定程度的持续偏离。对于加性故障II，AEKF 算法完全失去故障估计能力，导致工具面角估计完全偏离，无法达到可靠测量要求；文献[8]采用的SM-EKF 算法虽然可以快速跟踪加性故障II，但是波动太大，从表3 可以看出，该方法在一定程度上会造成较大的工具面角估计误差，无法满足实际钻井过程对工具面角测量的要求；而本文提出的ASM-EKF 算法可以快速准确地实现陀螺仪故障估计，在发生故障情况下，工具面角估计值的最大均方根误差为3.841°，满足实际钻井技术需求。

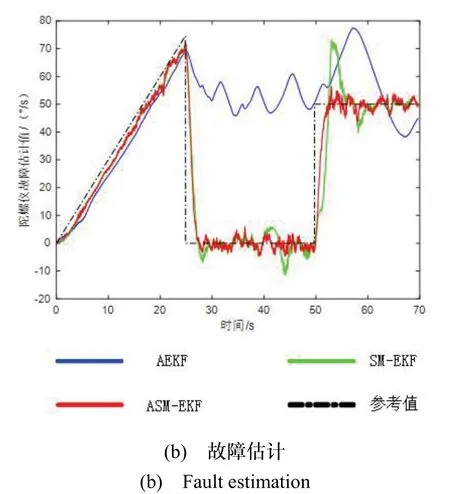
图8 加性故障II 实测效果Fig.8 Additive fault II measurement effect

4 结 论

为解决动态指向式旋转导向工具面角测量陀螺仪故障估计与处理问题，本文提出了一种自适应扩展集员卡尔曼滤波算法，实现了在陀螺仪发生加性故障情况下仍能够准确地测量工具面角。仿真和实验测试结果验证了该方法的有效性。主要结论如下：

1）获得了一种可靠测量工具面角的算法，在陀螺仪无故障时可以实现工具面角的准确测量，在陀螺仪发生加性故障情况时可以实时估计陀螺仪故障幅值，并对测量值进行补偿修正。持续故障与突变故障下工具面角测量的RMSE 分别为2.075 °、3.841 °，满足井下控制系统对工具面角测量精度的需求。

2）可以将线性化、陀螺仪漂移、井下振动等未知因素对井下传感器测量数据的影响等效成未知但有界误差项，SM-EKF 算法既有高效跟踪突变故障的能力、又有较高的滤波精度，可以用于同类井下测量数据的处理。

本文是在实验室进行的模拟测试，在振动强度以及振动变化规律等方面与实际钻井环境仍有差别，需要通过实际钻井环境进行测试，进一步提升该算法的实用性。