基于改进飞蛾扑火算法的无人机低空突防路径规划

黄 鹤，吴 琨，王会峰，杨 澜, 茹 锋，王 珺

（1. 长安大学 电子与控制工程学院，西安 710064； 2. 长安大学 西安市智慧高速公路信息融合与控制重点实验室，西安 710064； 3. 长安大学 信息工程学院，西安 710064）

无人机以低风险、高机动能力等特点被广泛地应用于军事领域，在执行任务规划中，低空突防技术是无人机协同作战以及网络化作战的关键技术，合理高效的突防方法可以使无人机更有效地躲避威胁区域，提高任务执行效率及生存几率，顺利完成飞行任务。

无人机突防以有效的规划路线方法[1]为基础，其核心取决于寻优算法的优劣。近年来国内外学者在该领域进行了大量的研究，提出了诸多有效的突防路径规划算法，如最速下降法[2]、Voronoi 图法[3]、遗传算法[4]、A*智能算法[5]等。目前最新、使用最广泛的方法是采用群体智能优化算法求解无人机突防路径的问题。唐立等提出了一种基于改进的蚁群算法的路径规划方法[6]，通过构造泰勒多边形构造路径可行解并建立路径安全度约束，缩小搜索范围，再通过蚁群算法寻找最优路线。该方法提升了寻优效率，但路径的精确度不高。宋宇等提出了一种基于三维规划的改进粒子群优化方法[7]，提升了全局及局部搜索性能，但由于将威胁场考虑的比较简单，并未考虑地形等因素，因此实际应用效果并不理想。近年来，许江波等通过自适应策略改进鱼群算法，利用其全局寻优能力解决路径规划问题[8]，但该算法的不足还是搜索时间过长。

同时，在三维无人机路径规划过程中，由于地形与威胁源的信息量大，使群体智能优化算法寻求最优路径时复杂度呈现指数上涨，极易陷入局部最优。而飞蛾扑火算法因其独特的寻优方式及更新策略可以在复杂度较高的情况下具备良好的寻优能力。因此，本文提出一种基于改进飞蛾扑火算法的三维无人机低空突防方法，在保证高精确度的情况下，尽量缩短寻优时间，快速有效地获得无人机突防的最优路径。

1 无人机三维突防环境建模

在处理静态三维环境的无人机突防问题时，最重要的是根据任务、威胁情况，以及地形等已知因素构建三维的地形和威胁环境约束。本文将基本地形、雷达监测、火炮威胁、无人机物理约束等进行数学建模，并通过数字融合，构建出三维环境下的地形约束。

1.1 地形约束

不同任务中，无人机面临的实际战场环境是不相同的，根据海拔不同，将地形分为平原地区，山地地区，丘陵地区三种地形，其中影响最大因素的是山峰，同时也要考虑海拔变化带来的影响。首先，三维环境下的山峰建模如下所示：

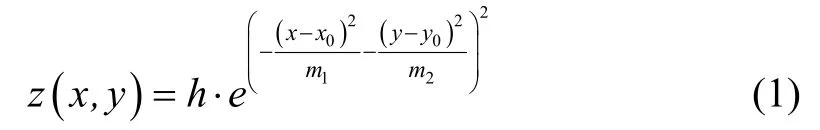
其中，(x,y)为山峰地形在水平平面上对应的坐标，(x0,y0)为山峰地形在水平平面上的中心点坐标，h为高度参数，m1和m2反应山峰的陡峭程度。另外，航迹点的地形威胁代价如下：

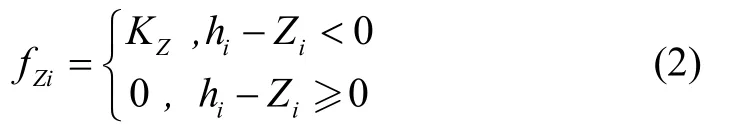
其中：Kz为地形威胁系数，hi为第i个航迹点的海拔高度，Hi为第i个航迹点距离地形的垂直高度，fzi为第i个航迹点对应的威胁代价。此外，无人机低空突防需考虑高程代价，航迹点的高程代价如式(3)所示：

无人机在突防中的地形约束还需要考虑到飞行边界范围以及最大飞行高度，保证操控无人机的安全性。因此设定无人机飞行水平范围为(Xmin，Ymin)和(Xmax，Ymax)，最大飞行高度为Hmax。

1.2 威胁模型约束

雷达、电磁威胁、导弹是无人机突防的主要威胁来源，具体建模如下：

(1) 雷达威胁

雷达主要通过电磁波来探测目标的距离，速度，相对位置等敌方信息，显然，要使无人机顺利突防，必须在飞行过程中避开雷达的探测范围，保证安全。

描述雷达方程特性的方程如下：

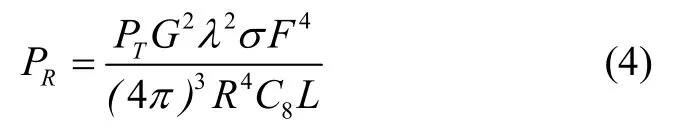
其中，主要因素是P，也就是目标和雷达之间的距离，因此雷达方程简化为雷达探测概率模型如下：

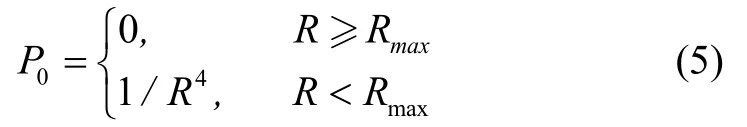
(2) 电磁威胁

一般情况下，电磁威胁可视作半球型，威胁模型如下：

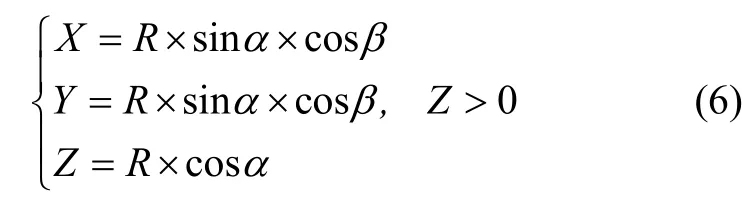
其中，R为电磁干扰的半径，α为Z 轴正向与半径的夹角，β为半径在水平面上的投影与X 轴正向的夹角。

(3) 导弹威胁

敌方导弹的威胁范围内也被称作禁飞区，必须躲避。在三维平面上，导弹威胁范围近似于一个半球体。 无人机在禁飞区半径内下被击中的可能性为：

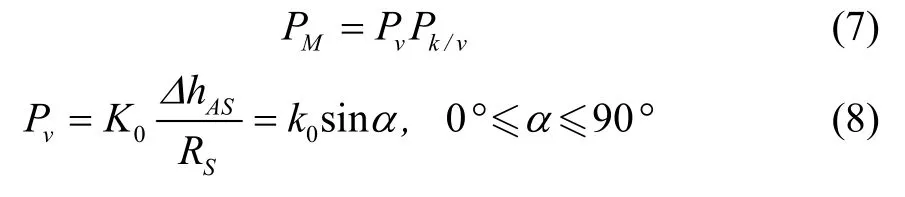
其中，Pk/v为常数，表示无人机在禁飞区半径内被摧毁的概率；K0为比例系数，Rs为导弹威胁中心与无人机之间的斜距；α为视线俯视角。则：

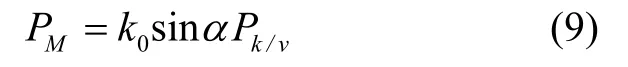
在三维建模过程中，威胁源半径较大，而无人机限高较低，因此可以将威胁源等效为圆柱地形处理[9]。航迹的威胁代价如下：

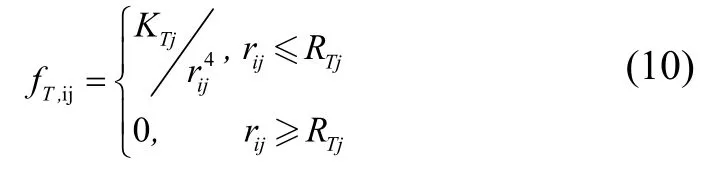
其中，KTj为威胁源j的威胁系数，rij为第i个航迹点到威胁源j中心的直线距离，RTj为威胁源j的威胁半径，FT,ij为第i个航迹点到威胁源j中心的代价。

1.3 无人机约束

无人机在飞行过程中受自身的物理约束，主要有最大转弯角α、最大下滑及爬升角β，以及燃油代价，中燃油代价用路程表示。各物理约束分别为：

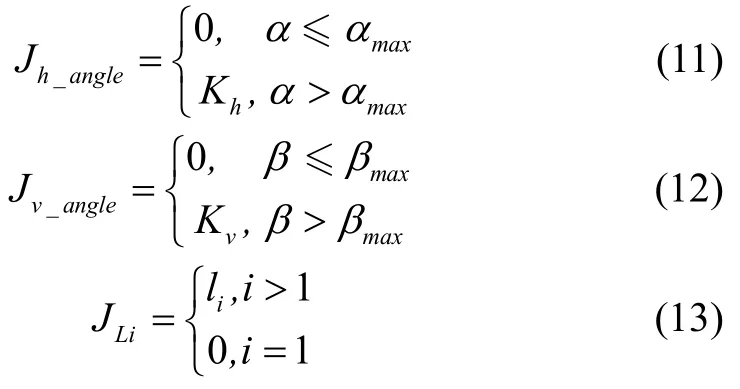
式中，Kh和Kv分别为转弯角和俯仰角威胁系数，Jh_angle,i和Jv_angle,i分别为第i个航迹点对应的α和β的代价函数。综合各代价函数，可得出第i个航迹点的无人机物理约束代价函数为：

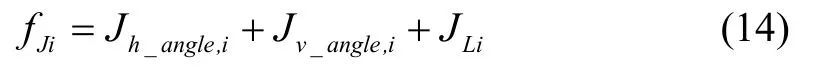
1.4 航迹代价函数

将地形约束、高程代价、威胁模型约束及无人机自身物理约束的代价加权综合起来就构成最终的无人机代价函数，如式(15)所示。

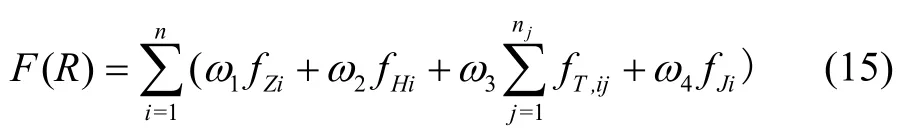
式中，F(R)为整条航迹的代价，ω1，ω2，ω3，ω4为各代价的权重。

2 改进的飞蛾扑火算法

2.1 飞蛾扑火算法

飞蛾扑火算法（Moth-flame Optimization, MFO）是受到飞蛾围绕火焰对数螺旋线形式运动的现象启发而提出的一种新型的元启发算法[10]。在算法中，飞蛾为待优化的问题，火焰为每次迭代的最优解，通过螺旋更新改变飞蛾自身的位置以及火焰的结构。

2.1.1 飞蛾种群的初始化

定义飞蛾的特征有d维，设初始飞蛾个数为n，路径点的个数为d，则飞蛾种群M如式(16)所示。

其中，定义Mi为飞蛾种群M中的第i只飞蛾。飞蛾适应度的大小由OM表示：

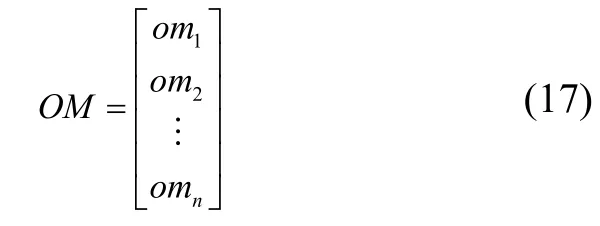
其中，Omi为第i只飞蛾的适应度，通过相应的代价函数得到。初始火焰的集合与M大小一致，并随着后续的迭代，火焰的数量会逐渐减小，火焰集合由F表示。

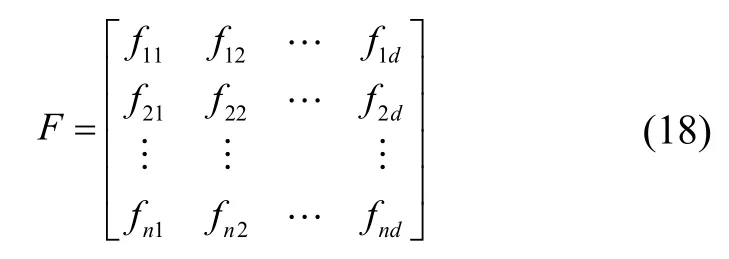
其中，第i个火焰由Fi表示。火焰的适应度值OF的大小同样为n×1，如式(19)所示。

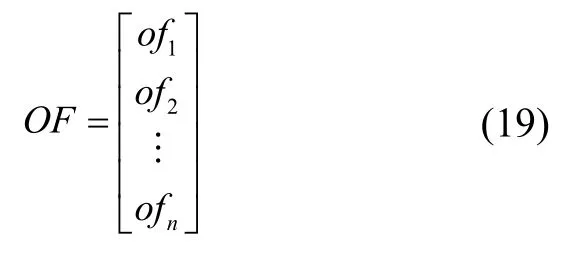
其中，ofi表示第i(i=1,2,…,n)个火焰的适应度值。OF矩阵是OM中每个向量排序之后的结果，所以F是M矩阵根据OF矩阵的排序得到的结果，这说明火焰F是飞蛾M在当前迭代搜索中的最优解。

2.1.2 迭代更新

MFO 算法每轮的更新机制可分为两个阶段：飞蛾扑火、飞蛾弃焰。

(1)飞蛾扑火：根据飞蛾的趋光性，飞蛾Mi围绕对应的火焰Fj做对数螺旋曲线运动。定义对数螺旋曲线如式(20)所示：

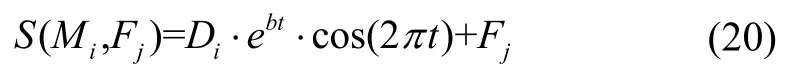
其中，S(Mi,Fj)是飞蛾更新后的新位置，Di是第j个火焰与第i只飞蛾的欧式距离，b为常数参数，可调整对数螺旋曲线，通常取1。参数t为[-1,1]范围内的一个随机数，表示当前飞蛾的更新位置与火焰的接近度，则t=-1 代表飞蛾与火焰最近，t=1 则两者相距最远。具体过程如图1 所示。

(2)飞蛾弃焰：为了提高算法的收敛速度并保证飞蛾种群向最优靠近，应逐渐减少较差的火焰，飞蛾仅围绕保留下来的火焰做旋转运动，从而避免飞蛾丢失最优解的情况。火焰自适应减少如公式(21)所示：

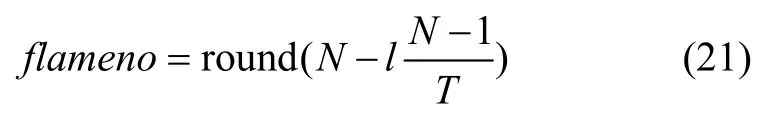
其中，flameno为当前火焰数量，N为种群数，l为当前的迭代次数，T为规定的最大迭代次数。

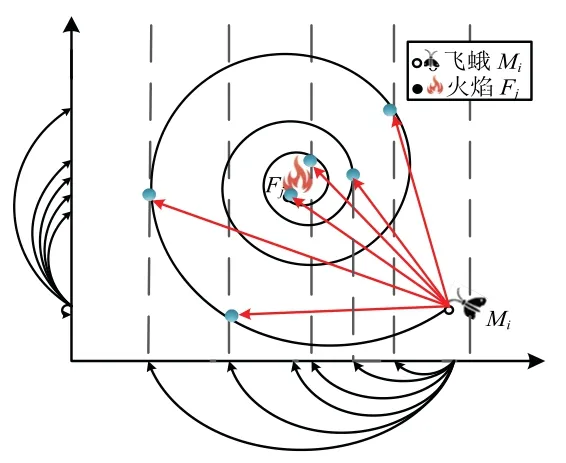
图1 飞蛾运动轨迹图Fig.1 Moth tracks

2.2 基于改进的MFO 算法的无人机三维路径规划

2.2.1 航迹编码

在实际应用中，每条路径都是由多个航迹点连接而成的线。定义种群中的一只飞蛾Mi即为一条路径，Mi=[mi1,mi2,……,min]，每个航迹点mi1具有空间三维的属性(x,y,z)。同时，在利用MFO 算法规划三维的无人机突防路径的问题时，首先确定航迹点数n，其次等距离x方向的航迹点坐标固定不变，通过对y和z坐标的寻优确定最优突防路线。

2.2.2 自适应惯性权重

惯性权重在平衡算法的全局及局部搜索能力中起着至关重要的作用。传统MFO 算法中的火焰并未能被充分利用，因此，本文在飞蛾的更新策略上引入了自适应权重。通常，在群体智能算法中自适应权重加在步长上，而本文改变其更新机制，通过将自适应权重放在火焰上扰动火焰的位置保证充分发挥最优解的优势。自适应权重ρ如下表示：

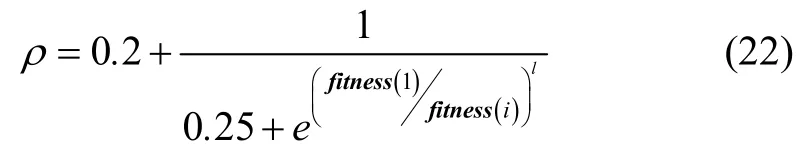
其中，fitness(i)为当前迭代中第i只飞蛾的适应度，l为当前迭代次数，当l逐渐增大时，自适应权重ρ趋向于1。引入权值后的位置更新策略如下：

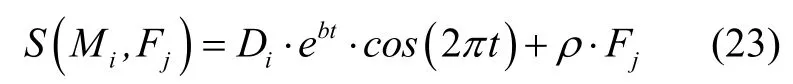
将自适应惯性权重策略引入进MFO 的位置更新机制中，在算法前期，使得不易于快速收敛到局部最优解，在迭代过程中跳出局部最优寻求全局最优。在寻优后期，权重趋向于1，保证局部最优解的精确度。

2.2.3 改进的交叉算子与变异算子

遗传算法在求解多峰函数及复杂问题时的高效性非常适合与MFO 相结合[11-13]。遗传算子主要包括三个方面：交叉算子、变异算子、遗传算子。针对MFO因自身寻优方法存在早熟性，在求解三维环境下最优路径时无法快速定位到最优路径等问题，本文将火焰矩阵与遗传算法的交叉算子、变异算子相结合并加以改进，使算法在前期快速跳出局部最优，增强算法的收敛性能。主要思想是每次迭代时将最优火焰与其余随机火焰进行交叉重组，并与原来父代的适应度作对比，若相对原来父代适应度较优，则替换父代。交叉算子表示如下：

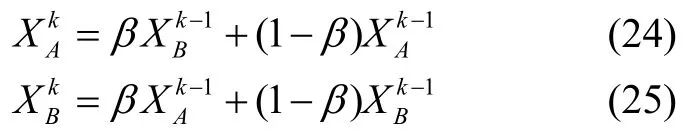
其中，XAk代表第k代火焰矩阵中的最优火焰个体，XBk表示此外的任一随机火焰个体，β为一系数，当β为常数时，称为均匀交叉算子，当β随迭代次数改变时，则称为非均匀交叉算子。

新一代的火焰个体主要由系数β及上一代的个体来共同决定，当β趋近于0.5 时，子代远离父代，可以拓宽搜索空间，保证火焰种群具有多样性，当β远离0.5 时，子代靠近父代，保证搜索范围缩小，使得精确度提高。因此，在交叉算子的基础上做如下做改进：

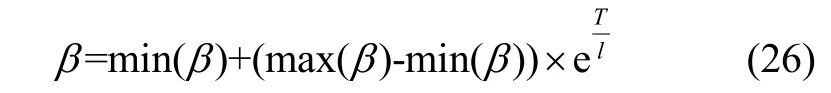
其中，min（β）及max（β）分别代表β的最大值及最小值。β系数曲线如图2 所示.

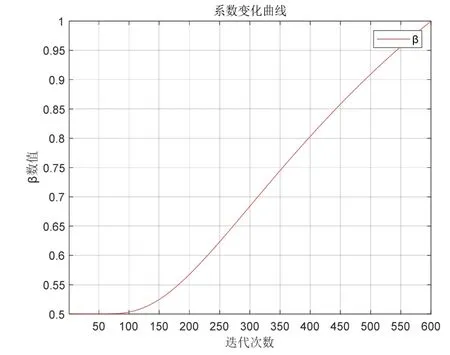
图2β 系数变化曲线图Fig.2 Curve of β coefficient change

由图2 可知，为了保证在迭代初期XA及XB在后代中有较为平均的基因占比，以及火焰矩阵的多样性，取β的初始值为0.5，并使其在前期增长缓慢。随迭代次数的增长β迅速靠近1，使种群多样性降低，搜索精度增加。

吕晓英(以下简称吕)：我的审美观念，或者说欣赏趣味，可能是属于比较传统的。我以为，小说、电影的中心应该是故事，音乐、歌曲的中心是旋律，我喜欢有故事性和旋律性的作品。而当今的许多作品却似乎背离了这种传统特征，小说、电影越来越不会讲述一个故事，音乐、歌曲也越来越不会演绎一段旋律。可能就因此，我和许多小说的潜在读者一样，逐渐放弃小说，喜欢看电视剧胜过看电影，因为在电视剧这种文化形态中，故事性被表现得最为充分。

（2）高斯变异算子

由于地形比较复杂，在MFO 寻优过程中，个别航迹点迭代时无法跳出局部最优，使航迹出现较大偏差，需加入高斯变异算子对航迹点随机干扰。设其中一个火焰为Fi=[f1f2...fd]，每一维度根据变异率p选择是否产生变异。假设第k维产生变异，则高斯变异算子为

其中，fk为火焰第k维的特征，f'k为变异后的特征，λ为系数，受空间大小影响，决定变异的程度大小。

2.3 三次样条插值平滑路径算法

在无人机实际飞行中，为了保证无航迹转弯角平滑，避免无人机受到自身物理约束及性能的限制，采用三次样条改善最终突防路径。设最终无人机突防路径为：Z=(z1,z2……zn)，每个路径点zk(k=1……n)有(x,y,z)三个维度，分别对(x1,x2……xn)、(y1,y2……yn)、(z1,z2……zn)做三次样条插值，最终形成一条光滑路径，三次样条插值效果如图3 所示。

图3 三次样条插值优化效果图Fig.3 Cubic spline interpolation optimization effect diagram

总的算法流程如表1 和图4 所示。

表1 本文算法流程Tab.1 Algorithm flow of this paper

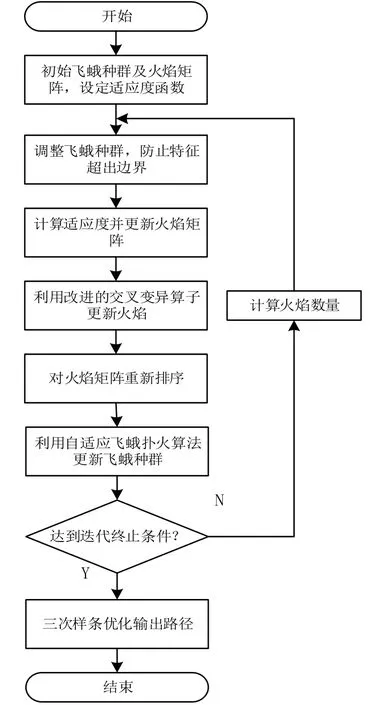
图4 本文算法流程图Fig.4 The flow chart of this algorithm

3 改进的飞蛾扑火算法对比实验

3.1 测试函数

由于无人机面对复杂地形突防时，多极值的寻优性能非常关键。选择使用基准测试函数中两个单峰函数Quartic 和Sum Squares 及两个多峰函数Penalized1和Penalized2 来评估算法性能，它们能在复杂度较高的情况下验证算法能否跳出局部最优。测试函数描述如下：

(1) Quartic 函数

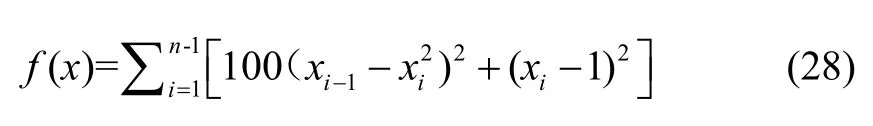
(2) Sum Squares 函数

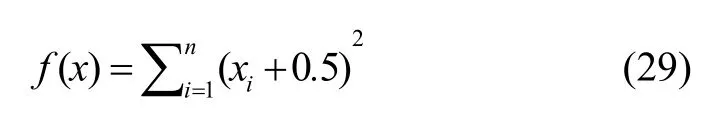
其中，xi∈[-100,100],n=10, 全局最小值处为（0,0…0）。

(3) Penalized 1 函数

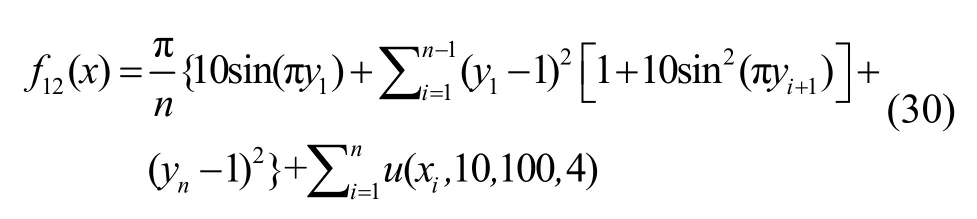
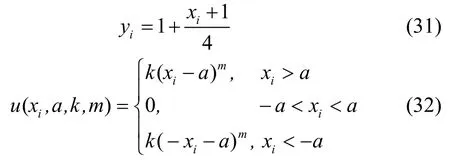
其中，xi∈[-30, 30]，n=10，全局最小值处为（0,0…0）。

(4) Penalized 2 函数

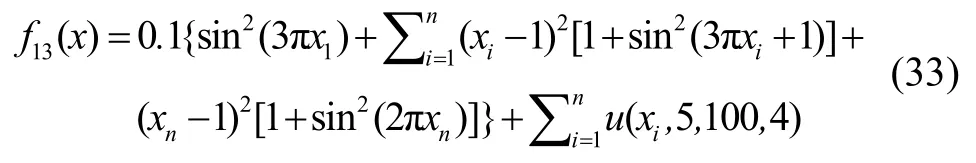
其中，xi∈[-30,30]，n=10, 全局最小值处为（0,0…0）。

3.2 实验验证

采用上述4 种测试函数分别评估MFO 算法、灰狼算法(Grey Wolf Optimizer, GWO)算法[14]以及本文算法的寻优性能。图5 为各算法在不同测试函数上的适应度曲线图，表2 列出了各算法经过测试函数20次测试的均值及最优值。

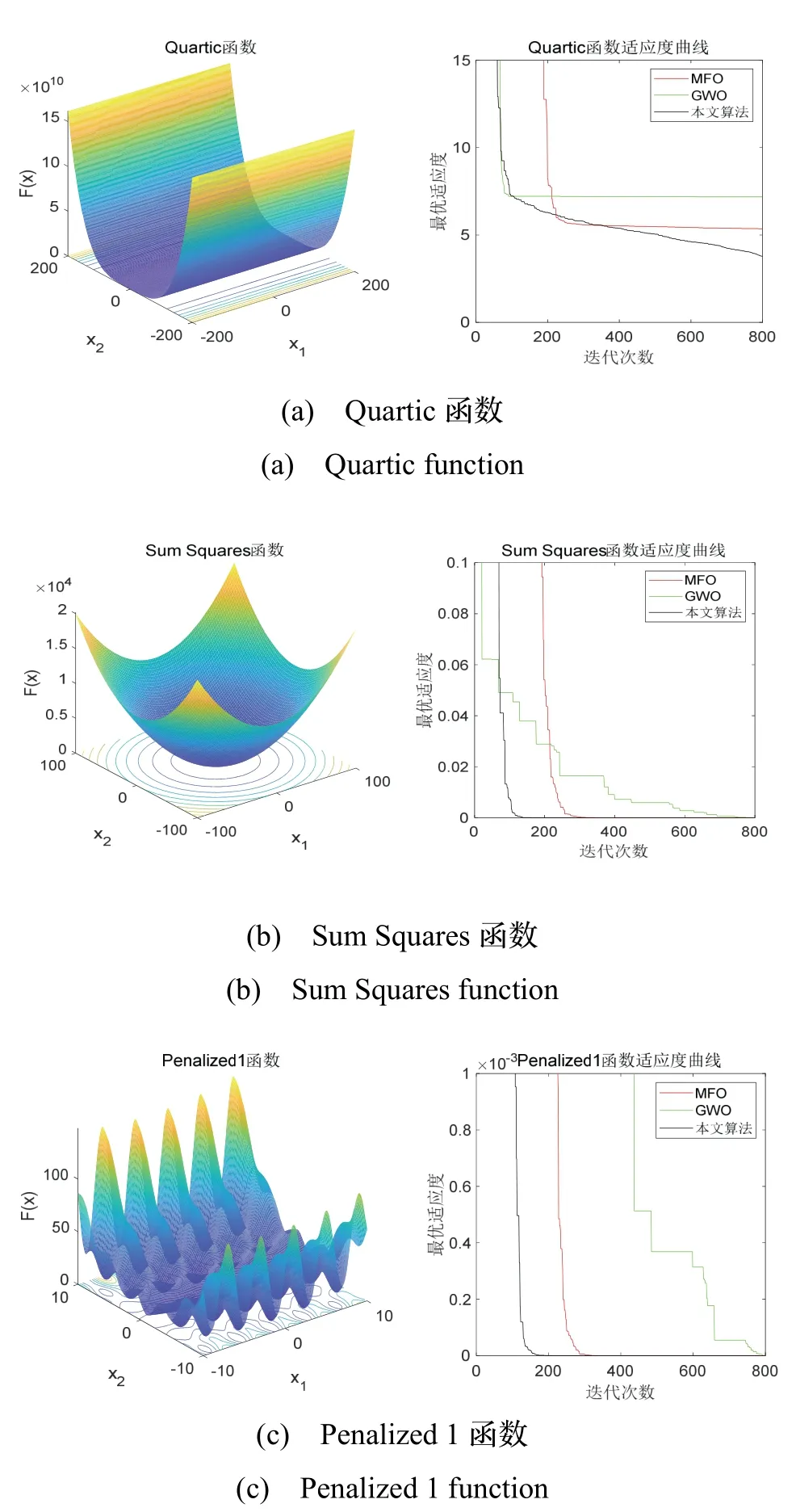
由图5 可知，GWO 在Quartic 函数上的寻优性能相比于MFO 较好，在其余测试函数上收敛速度及精度均不如MFO，而本文算法在各测试函数上收敛速度及精度均优于其余两种算法，说明本文算法在复杂度较高的测试函数上有较强的寻优能力。由表2 可知，MFO 在Quartic 函数上表现较差，其余测试函数上最优值虽较好，但均值与最优值相差较大，波动明显。GWO 在多峰测试函数上精度较低，但较为稳定。而本文算法在各多峰函数上精度相比于MFO 及GWO均有较大提升，并且寻优稳定。这说明，本文提出的改进方法可以有效帮助MFO 算法跳出局部最优解，增强了MFO 算法面对复杂问题时的全局寻优能力。

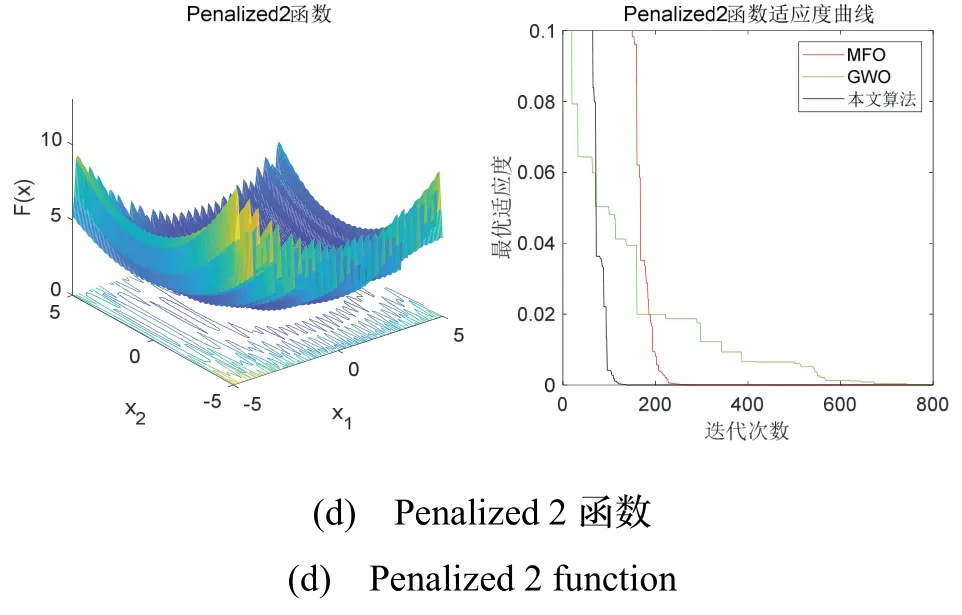
图5 各算法在测试函数上的适应度曲线图Fig.5 The fitness curve of each algorithm on test function

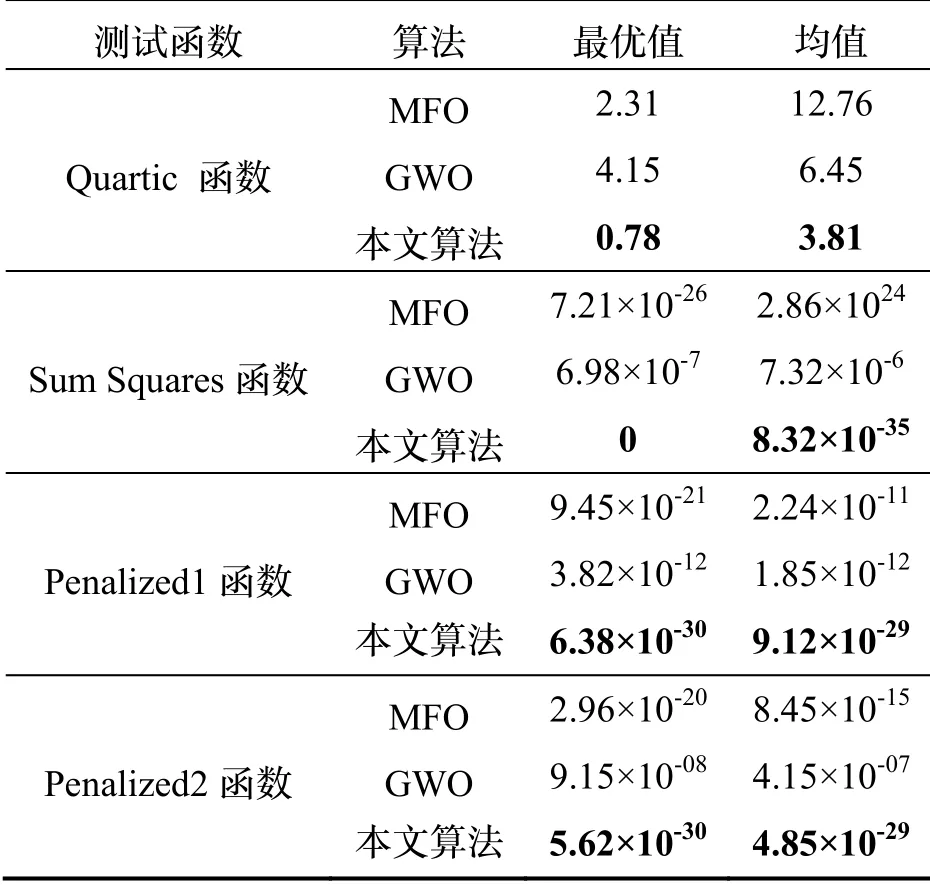
表2 三种算法在测试函数上的实验对比Tab.2 Experimental comparison of three algorithms on test functions

4 无人机突防仿真测试及分析

仿真测试计算机的CPU 为Intel Core i7-9750U CPU 2.60GHz、内存为16GB，操作系统为Windows10，编译软件为Matlab R2018a。测试地形区域大小为100 km×100 km,测试限高为4 km。无人机航线的起始点与终止目标分别为(1, 3, 0.5)及(99, 98, 0.5)，敌方雷达及火炮距离的中心为(20, 13.5, 0)、(85, 60, 0)、(40, 59, 0)，作用半径为9 km。MFO、GWO 和本文算法求得三条路径的航迹点分别用圆圈、星号、及正方形表示。各算法种群数设为100，最大迭代次数为800 次。算法参数以及无人机突防轨迹图分别如表3和图6 所示。

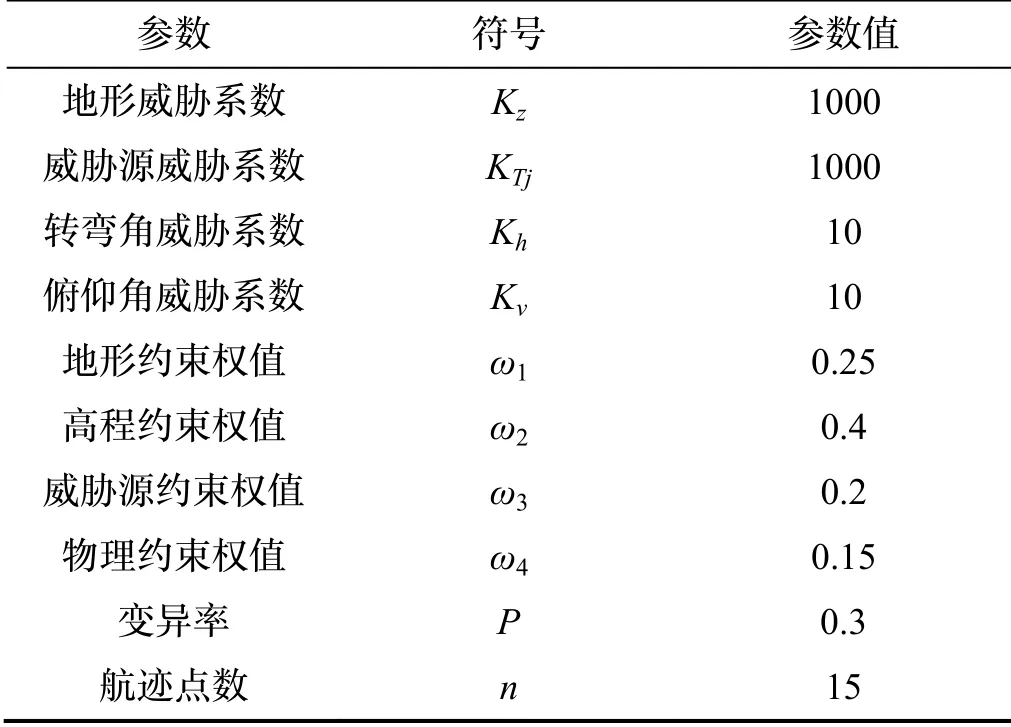
表3 主要参数Tab.3 Main parameters

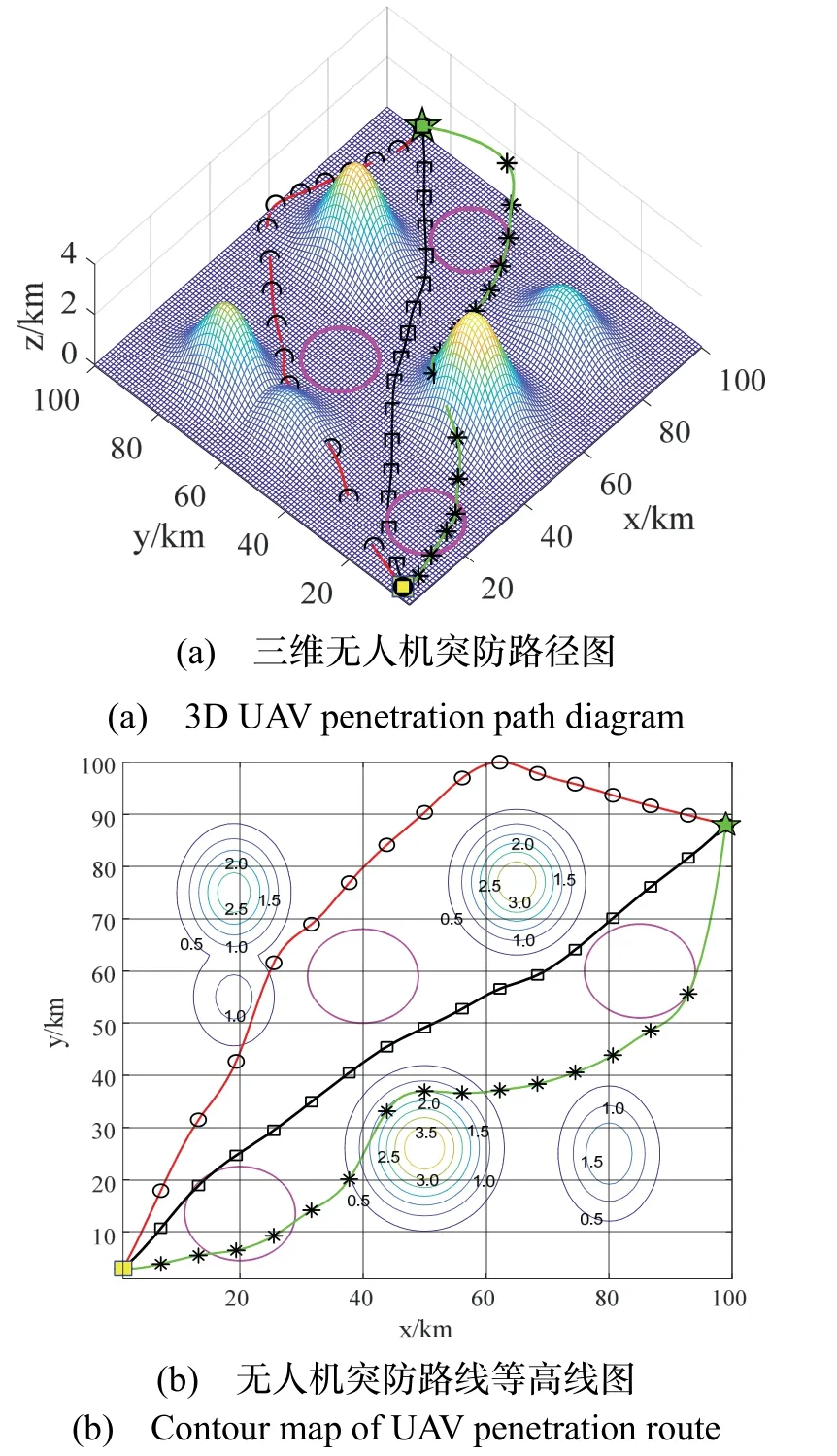
图6 无人机突防路线轨迹图Fig.6 Path map of UAV penetration route

通过MFO、GWO、本文算法在无人机突防路线轨迹图中的对比可以看出，传统MFO 规避了威胁源，但路径中有部分穿过了地形，规划的路线较长；GWO的规划路线普遍飞行高度高，穿过了第一个威胁源，对无人机自身的物理约束没有满足，俯仰角过大；而本文算法可以有效地利用地形优势，在规避山峰地形及各威胁源的同时，满足无人机自身的物理约束，并做到贴地飞行，避免路径中出现多余路线，从而达到低空突防的目的。算法的航程和最优代价如表4 所示，最优航线代价变化如图5 所示。

表4 算法航程及最优代价Tab.4 Algorithm voyage and optimal cost

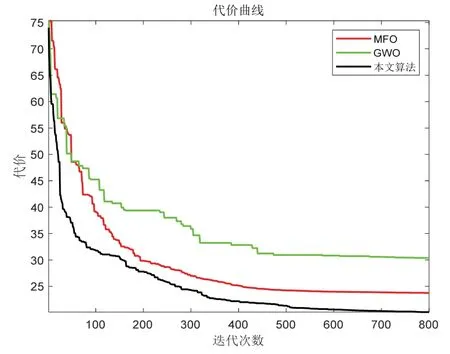
图7 最优路线代价变化图Fig.7 Optimal route cost change graph

仿真结果表明，MFO 在寻优前期可以跳出局部最优，但收敛速度相对较慢，在迭代到400 次左右陷入局部最优，求得的突防路径最长；GWO 在复杂度较高的情况下效果较差，寻优过程中难以跳出局部极值，且精度较低，难以适应三维地形下无人机突防路径规划；而本文算法无论在精度、速度方面，都优于MFO及GWO，最短路径比MFO 及GWO 算法分别降低了25.14 km 和14.77 km，求得路径最短，代价分别降低了3.63 及10.25。通过算法比较，本文算法可以更为有效地避开威胁地形及威胁源，利用地形作掩护实现低空突防。

5 结 论

本文针对无人机的低空突防路径规划问题，提出了一种基于改进MFO 的三维无人机低空突防方法。首先，建立三维地形模型、威胁源模型及无人机物理约束模型，确定威胁代价函数。其次，针对MFO 算法易发生早熟收敛，收敛速度慢，陷入局部最优等问题，提出了两种改进思路：(1)利用自适应权重改变MFO 的更新轨迹，加快算法的收敛速度并改善局部搜索性能；(2)在MFO 中引入交叉算子和变异算子，扩大搜索空间，进一步提升了算法精度，有效解决了MFO 自身缺陷。最后，利用三次样条插值改善突防路径，最大程度避免无人机受到自身物理约束的限制。实验表明，该方法可以更精确、快速地使无人机自主避开危险区域选择最优路径，实现低空突防。