基于激光干涉的微重力加速度测量方法

段文祥，李 楠，董文博

（1. 中国科学院大学，北京 100049； 2. 中国科学院太空应用重点实验室，中国科学院空间应用工程与技术中心，北京 100094）

在太空中的飞行器，围绕地球运行时，其受到的引力和离心力相互抵消，飞行器表现为“失重”。但飞行器由于受到空气阻力、科里奥利力、潮汐力等剩余外力干扰，以及飞行器运动过程中内部仪器振动造成的扰动，使飞行器表现出受到的合力不为零的情况，这被称之为微重力[1]。为了利用微重力环境进行科学实验，通常在地面上通过落塔来模拟微重力环境[2]。在落塔微重力环境中，微重力量级一般为10-5-10-3g（g为地面重力加速度，约为9.8 m/s2）[3,4]。为了测量微重力加速度，一般使用力平衡式加速度计测量。石英加速度计测量带宽高，范围在0.01-200 Hz，但精度较差。一般的石英加速度计误差可以达到10 μg，零偏值甚至达到10 mg，在每次使用前，都需要根据使用温度进行标定，确定零偏值。静电悬浮加速度计测量频率较低，范围在0.0001-10 Hz，精度较高，分辨率一般为0.1 μg，但价格昂贵，测量量程较小[5]。利用激光干涉原理进行微重力测量可以有效地解决石英加速度计和静电悬浮加速度计存在的问题。

激光干涉技术常用于绝对重力仪。绝对重力仪对于测量地球表面的精确重力加速度值、获取地表的高精度绝对重力观测资料、资源勘探、地球科学研究、地震监测预报、精密计量、飞行器导航等有着重要的作用。目前，国外研究绝对重力仪的国家有美国，俄罗斯，日本、德国、意大利等[6]，其中美国的Micro-g公司研制出的FG5型绝对重力仪和A10型绝对重力仪是目前测量精度较高、并且商业化的绝对重力仪，FG5型绝对重力仪精度可达1-2 μGal（Gal 为重力测量单位，1 Gal=10-2m/s2），A10 型绝对重力仪精度可达10 μGal[7]。国内研制的绝对重力仪有清华大学研制的T-1 型绝对重力仪，中国计量科学研究院研制的NIM系列绝对重力仪，此外，中国科学院测量与地球物理研究所、中国科学院地质与地球物理研究所、中国地震局地震研究所等也研制了或正在研制绝对重力仪[8]。华中科技大学尝试通过迈克尔逊干涉仪测量了落塔微重力水平，其依托微重力下落的实验结果也说明了激光干涉测量微重力方法的可行性，但每次实验只测量一个重力值，不考虑测量的动态特性[9]。

本文受到激光干涉技术测量绝对重力的启发，改进了马赫-曾德尔干涉仪，设计了新的基于激光干涉的微重力测量光路。激光束通过干涉光路在光电探测器上形成干涉条纹，通过测量干涉条纹的电压值变化确定角锥棱镜位移，进而通过软件拟合，得到实际的加速度值。相较于传统的绝对重力测量仪，新设计的基于激光干涉测量微重力仪器改进了马赫曾-德尔干涉仪光路，使之更加紧凑，更加小型化，这种方法使得激光干涉测量微重力成为可能。在微重力环境下，通过电机控制角锥棱镜上升并与真空舱一体化，优化算法参数，实现了新的激光干涉测量微重力的方法。

这种方法的优势在于能够测量绝对微重力，无系统零偏值，而且可以在较高的测量频率下连续输出加速度值，并且具有较高精度。搭建了地面微重力模拟实验平台，实验结果显示，通过使用激光干涉技术测量微重力的结果与理论分析符合，证明这种激光干涉测量微重力的方法是有效的。

1 测量原理

1.1 激光干涉测量原理

通过对已有的绝对重力仪干涉光路进行对比，发现大部分自由落体绝对重力仪的光路设计采用迈克尔逊干涉仪，少部分采用马赫-曾德尔干涉仪。与迈克尔逊干涉仪对比，马赫-曾德尔干涉仪两道光的路径可以完全地分离,使受测物在安排时更有弹性；透明受测物受到多道反射光的干扰较小,而迈克尔逊干涉仪的光路由于来回都是同一条路,掺杂噪声光比较多。马赫-曾德尔干涉仪可以用来观测从单独光源发射的光束分裂成两道准直光束之后，经过不同路径与介质所产生的相对相移变化。在测量微重力水平时，可以将一束光作为参考光，分析经角锥棱镜的光束相对参考光的干涉变化，进而得到角锥棱镜的运动情况[10]。

基于马赫-曾德尔干涉仪，设计如图1 所示光路，利用该光路进行微重力测量的原理如下：激光器输出光束，通过扩束器扩束，光束经反射镜1 反射后到达反射镜2，通过玻璃窗2 后到达分束器1，其中一束光向左到达分束器2 作为参考光臂，另一束光向上到达角锥棱镜，经角锥棱镜反射后到达分束器2，与参考光合束干涉，通过玻璃窗3 后，到达光电探测器处，探测器将光强转换为电压值。水平液面的作用为光路调节时用来保证设备垂直度。实际搭建的微重力测量平台如图2 所示。

图1 激光干涉光路Fig.1 Laser interference path

图2 微重力测量平台结构图Fig.2 Structure diagram of microgravity measuring platform

在微重力测量的过程中，角锥棱镜做自由落体运动。角锥棱镜位移Δh与视场中心移动条纹的数目N、激光波长λ 的关系为：

其中λ为激光器波长，我们选用的激光器波长为633 nm。式(1)对时间求导可得角锥棱镜的速度v与干涉仪输出干涉条纹频率fi的关系：

1.2 信号采集处理系统

角锥棱镜与电机脱离后进行自由落体运动，测量光路与角锥棱镜发生相对位移，到达光电探测器处两束光的光程差不断地发生变化，放大器放大信号，通过高速数据采集板得到时间与电压的关系，然后进行数据处理，根据式(2)对数据滤波，得到过零点检测时间与条纹移动个数的关系，然后通过软件拟合数据，得到微重力加速度变化的情况。

图3 信号采集系统原理图Fig.3 Schematic diagram of signal acquisition system

1.3 微重力数据解算方法

通过高速数据采集板可以得到时间与电压的关系。由于每经过一次明暗变化，位移发生半个波长的变化，所以采用过零检测法来计算物体运动过程中过零点时间，然后根据过零点时间序列计算时间位移对，最后对数据进行二次拟合得到微重力加速度[11]。

过零检测法指的是计算干涉条纹过零点时间，由于条纹过零点为条纹穿过横轴的位置，因此过零点必然在两个幅值符号相反的采样点之间，即电压需要满足式(3)。

找到数据中所有幅值满足Ui、Ui+1的数据对，通过式(4)。

即可计算所有的条纹过零时间t。其中，ti为第i个采样点时间，由式(5)计算得到，Ui为ti对应的电压值，Ts为采样周期。

通过信号采集系统得到一系列的过零点时间序列，将数据输入信号处理系统，软件生成一系列与时间序列对应的等间隔的位移序列xi(i= 1, 2, 3……)，获得角锥棱镜运动过程中的时间位移对。以式(6)为观测方程，

将时间位移对进行最小二乘拟合，根据拟合结果的一次系数和二次系数，计算后就得到实验过程中速度和微重力加速度。

2 激光干涉测量精度分析

使用激光干涉技术测量微重力，需要得到测量时各种因素对微重力测量的影响，保证激光干涉测量微重力的精度[12]。

首先，由位移x和时间t得到加速度a

误差传递公式（σa为标准偏差）：

代入得加速度公式：

根据式(9)，可以得出：

从以上公式可以看出σa/a受到σt、t、σx、x的综合影响。对各部分影响分析如下：

（1）相对时间精度σt/t的影响

对于普通的晶振，σt/t在10-4量级以下，精密原子钟，σt/t在10-6量级以下。对于微重力测量，测量值不超过 10 mg，若要求 μg量级，只需要满足σa/a=10-4，因此，在实际测量中，普通晶振已经完全可以满足精度，而用高精度的原子钟可以到10-6量级。

（2）σt极限值的影响

在（1）中σt/t只能给出相对误差，而当测量频率很高（t非常小）时，还需要考虑σt的极限值。例如，当σt为一定值10-6s 时，精度和频率有以下关系：

此时，当测量频率f=1 Hz 时，精度σa/a还可以在10-6量级，当测量频率f=100 Hz 时，考虑到σt的极限，精度σa/a只能在10-4量级。测量频率越高，精度越低。

（3）相对位移精度σx/x的影响

位移的绝对精度偏差取决于激光器本身的频率稳定性以及干涉光路测量的光程差。结合仪器设计（光程差小于50 cm），选择普通HeNe 激光器，使得σx/x在10-6量级以下，通过激光器长时间开机，可以使得这一数值进一步降低。如果更换为频率稳定型HeNe激光器，可以获得更高的测量精度。该影响因素基本可以忽略。

（4）σx极限值的影响

同（2）分析的一样，σx其极限值决定于一个周期过零点的精度或细分的精度，而这个精度决定于光电信号幅值Upp的精度和噪声。在一个周期中，σx=λarcsin(σU/Upp)。考虑到arcsin(U/Upp)的特性，只有当U/Upp比较小时（U0过零点处），才可以近似x=λU/U0；而在正弦的最大值处，这项的精度很低。一般地，对于光电噪声和AD 采集信号，滤波后U/U0可以达到10-3的精度。而λ在μm 量级，因此，σx= 10-3λ总体精度在10-9m 以下。

代入精度公式(11)可得：

测量频率f=1 Hz 时，精度影响约0.0002 μg；测量频率f=100 Hz 时，精度影响约2 μg，相当于测量值的10-6的精度。

（5）速度的影响和细分的价值

（1）-（4）是理想情况。但实际测量场景中，要保证准确测量，每个周期至少要采集到三个过零点。当物体移动速度小于0.1 mm/s，且测量频率100 Hz的情况下，无法保障。

当角锥棱镜最大速度0.0078 m/s（0.2 mg微重力下降落4 s）时，采用633 nm 激光，其对应每秒的干涉变化为0.0078 m/s/633 nm/2≈24645，即24645 次干涉条纹变化。若将半个激光波长细分为5 等分，则每秒采样24645*5=123225 次（约124 kHz）。

可见，采用过零点的细分可以进一步提高测量精度和减小速度约束；若提高过零点的精度及细分方法，经验值可以提高一个量级。

（6）机械误差和不垂直度

如果激光干涉仪或棱镜不在垂直方向，则该因素影响整个测量标度值。(a-σa)/a= cosθ，如果偏斜角度θ=1°时，σa≈1.5×10-4；偏斜角度θ=0.1 °时，σa≈1.5×10-6。因此，此项影响很小。

（7）下落距离设计

假设测量被测物体微重力10 mg左右，则棱镜的下落距离约为x= 1/2at2= 0.8 m，如果测量内舱10 μg左右，则棱镜的下落距离约0.8 mm。

3 仿真分析

3.1 模拟数据生成

模拟落塔释放过程如图4 所示。实验开始时，通过电磁弹射的方式，弹射设备整体，然后设备内部电机弹射，给予角锥棱镜一个竖直向上的初速度，光电探测器根据干涉条纹变化输出电压值，AD 采集卡采集光电探测器输出的数据。

图4 落塔实验模拟示意图Fig.4 The release process

在实验过程中，真空舱内部抽真空处理，内舱受到空气阻力（f∝Av2）[13]及电机振动(频率4 Hz-10 Hz)的影响，内舱的微重力水平主要由空气阻力、电机振动所决定，而真空舱内部的角锥棱镜由于是在真空环境中自由下落，其加速度水平为当地重力加速度。

开始时，真空舱与角锥棱镜相对初速度为v，在上升过程中内舱受到空气阻力和电机振动影响，导致内舱与角锥棱镜加速度不同，真空舱与角锥棱镜之间的速度逐渐变大，在达到最大值之后，内舱减速，角锥棱镜与干涉光路相对速度逐渐减小至零；在下落过程角锥棱镜与干涉光路相对速度逐渐变大。由式(2)得，物体的速度与频率正比例相关，通过光电探测器测量得到的电信号变化频率，经过了从小变大再变小的变化。仿真微重力加速度变化如图5(a)。通过对加速度的分析，可以近似得到角锥棱镜和光路相对速度的变化，如图5(b)。

图5 落塔内物体运动过程分析Fig.5 Analysis of movement process of objects in falling tower

光电探测器探测到光强变化，转化为电信号，放大后在经过AD 采集卡转换后，接收到的二进制数据经过预处理后，得到原始数据，如图5(c),由于电信号本身具有一定噪声，根据式(2)，通过带通滤波处理，滤掉电噪声，得到结果如图5(d)。

3.2 模拟数据处理和分析

数值模拟过程如图6 所示。干涉信号经光电探测器采集转换得到电信号，AD 采集卡对电信号处理后得到模拟电信号，模拟电信号经软件拟合处理，求解得到加速度。

图6 数值模拟流程图Fig.6 Flow chart of numerical simulation

模拟过程如下，电磁弹射初速度为20 m/s，弹射下落舱0.1 s 后，真空舱内电机工作，弹射角锥棱镜，初速度为2 m/s，之后通过125 kHz AD 采集卡采集数据，在测量频率100 Hz 时，通过激光干涉测量数据，拟合得到加速度值，如图7。

图7 实际测量得到的加速度水平Fig.7 The actual measured level of acceleration

通过多次测量，得到激光干涉微重力加速度计与理论值的误差，如图8(a)。经分析，实验相对误差大于0.1%。为提高测量实验结果精度，提出进一步采用加大滤波周期的方法对实验数据进行处理。如图8(b)，数据滤波周期加大后，实验误差明显下降。

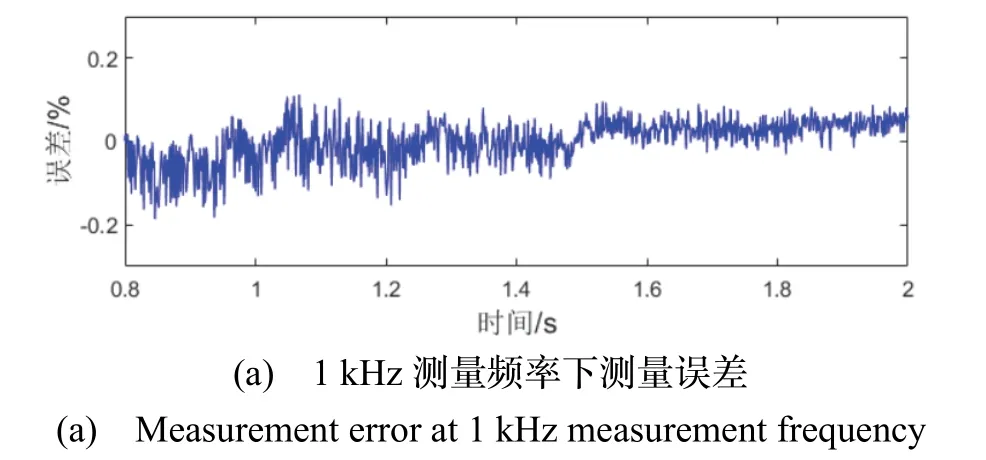
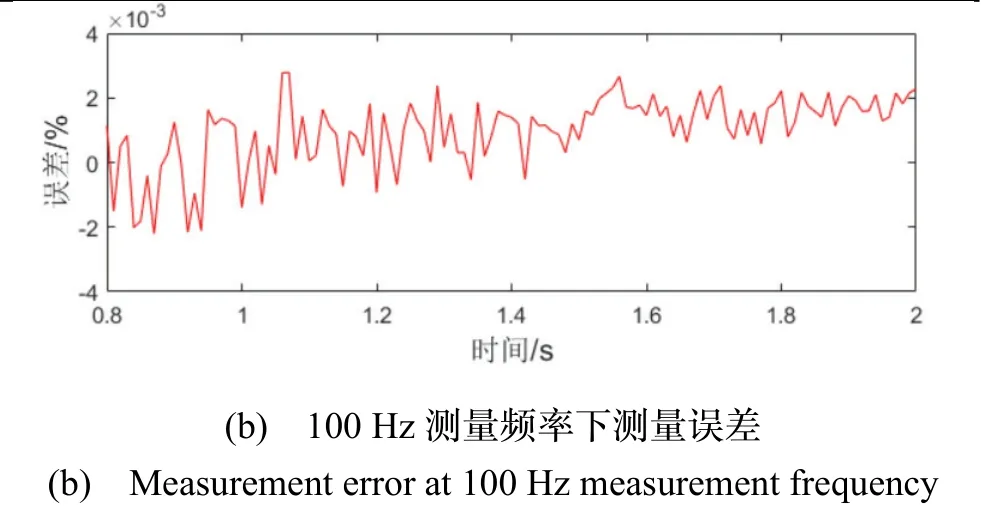
图8 125 kHz 采样频率下，测量频率不同时测量误差对比Fig.8 Comparison of measurement errors at different measurement frequencies in125 kHz sampling frequency

多次仿真10 MHz 采样频率下，不同测量频率拟合误差如表1 所示。得到以下结论：相同采样频率下，测量频率越低，数据拟合结果误差越小，越符合真实值。这是由于单次拟合数据量更多，对物体运动状态描画更清晰，拟合结果更符合真实结果，误差更小。根据仿真结果可以看出，当测量频率为1 Hz时，仿真结果精度在测量值的10-6量级；当测量频率为100 Hz 时，精度在测量值的10-4量级。

表1 不同测量频率下拟合误差比较（g= 9.8 m/s2）Tab.1 Comparison of fitting errors at different measurement frequencies (g=9.8 m/s2)

4 实际测量

4.1 重力加速度测量

在测量重力加速度时，采用电磁铁吸附角锥棱镜，AD 采集卡以10 MHz 采样频率采集光电探测器的电压数据，当电磁铁断电后，角锥棱镜自由下落。对采集得到的数据进行处理，得到加速度值。实验数据如图9 所示。（测量地重力加速度g为9.8015 m/s2）

图9 自由落体运动中原始数据Fig.9 Raw data in free fall

图10 实测重力加速度与去除空气影响后结果Fig.10 Measured acceleration of gravity and results after removing the influence of air

在运动过程中，角锥棱镜主要受到空气阻力F影响，如式(14)所示：

角锥棱镜底面直径d约为50 mm，质量m 约为50 g，实验空气密度ρ约为1.293 kg/m3，空气阻力系数C约为0.7[14]，g0为观测得到的重力加速度值。去除空气阻力影响，得到修正后的加速度值g'，如式(15)所示。

两次测量结果如图10 所示，由于角锥棱镜在空气中下落，不同的时间空气状况不同，因此两次实验结果有略微差异。实验结果基本证明了基于激光干涉测量加速度的可行性。

4.2 微重力测量

在实际测量中，通过三米电机[15]模拟微重力环境，如图11。实验开始前，设备整体位于电机顶部，角锥棱镜被电磁铁吸附处于真空筒顶部。实验开始，首先软件数据采集系统开始工作，电磁铁断电释放角锥棱镜，一段时间（大约0.08 s）后，电机向下以1g加速度运动，AD 采集卡以10 MHz 采样频率获取光电探测器的电压数据，软件拟合计算加速度值。模拟的微重力环境加速度值约为0.1g，为验证激光干涉测量微重力的方法的有效性，采用石英加速度计同时测量微重力。

图11 微重力实验环境Fig.11 Microgravity experimental environment

通过对上述实验数据处理后，得到的结果对比如图12。通过与石英加速度计的对比，发现两种测量方法在测量过程中加速度值基本一致，说明基于激光干涉的微重力仪可以测量微重力加速度值。

图12 微重力实验过程中测得的微重力加速度数据Fig.12 Microgravity acceleration data measured in the microgravity experiment

需要说明的是，由于实验硬件的限制，测量精度与理论值会有一定差距；角锥棱镜在空气中运动，由于在实验过程中角锥棱镜和实验光路相对速度较小，且空气阻力相较于电机本身振动导致的噪声量级较小，可以忽略；由于电机结构等噪声，实际加速度噪声很大。实验的结果说明了激光干涉测量微重力方法的可行性。

5 结 论

针对微重力测量领域中，传统加速度计只能测量相对加速度，以及存在测量精度低的问题，受绝对重力仪的启发，本文设计了一种新型激光干涉微重力测量仪器，并进行测量误差分析；提出利用电磁释放角锥棱镜的方式，保证了实验过程稳定可靠；在测量结果分析中，对结果精确度较低的情况，通过降低测量频率，提高了实验的精度，经过分析，在100 Hz 时，精度可以达到测量值的10-4量级，在1 Hz 时，精度可以达到测量值的10-6量级；研制了小型化的地面样机，并通过地面重力加速度实验以及小型落塔设备进行微重力实验，证明了利用激光干涉仪测量微重力加速度的可行性。与传统微重力测量手段相比，本文的微重力测量方法，为微重力测量方法提供了一种新的思路。