基于傅里叶级数拟合实现的三电平SHEPWM
李颖川,王琛琛,董志强
(北京交通大学电气工程学院,北京 100044)
随着现代工业的快速发展,三电平中点箝位NPC(neutral point clamped)型逆变器作为多电平逆变器之一,凭借其输出谐波含量低和开关器件承受的电压应力小等优势,在中高压和大功率场合中广泛应用[1-2]。
在大功率场合,为降低逆变器的损耗,需降低开关器件的开关频率,但在低开关频率下,常规的载波调制和空间矢量调制已经无法适用[3]。为满足系统在低开关频率下的运行要求,研究学者提出特定谐波消除脉宽调制SHEPWM(specific harmonic elimination pulse width modulation)法和电流谐波最小脉宽调制CHM-PWM(current harmonic minimum pulse width modulation)法[4]等优化PWM 法,其中SHEPWM 应用最为广泛。
SHEPWM 目前常用的实现方式有在线实现和离线计算,其中离线计算分为查表法和曲线拟合法。但两电平SHEPWM 与三电平SHEPWM 相比,其开关角轨迹的线性程度更高,采用多项式曲线拟合法较为简便,而三电平SHEPWM 的开关角轨迹变化较大,查表法与多项式曲线拟合法都存在缺点。如文献[5]采用两种方法实现三电平SHEPWM 的在线计算,其中:第一种为查表法与线性插值法相结合,减少查表数量,但表格数据的数量较多;第二种是将开关角轨迹拟合得开关角度,使用所得开关角度作为牛顿迭代的初值,利用牛顿迭代法在线求解开关角度,但会出现迭代不收敛的情况。文献[6]采用多项式曲线拟合法实现三电平SHEPWM,但在高调制比区域,需多段拟合才能达到拟合精度的要求。由此,研究学者提出了其他实现三电平SHEPWM 的方式。如文献[7]采用基于遗传算法的在线计算开关角的方法,计算过程中无需给定初值和预测解的变化趋势,易收敛且计算时间缩短,但实现过程较为复杂;文献[8]采用基于遗传算法优化的BP(back propagation)神经网络实现在线计算,计算时间短,且无需给定初值,但实现较为麻烦。
与多项式曲线拟合法类似,傅里叶级数拟合法可用于拟合曲线,多用于铁路客运量、自然灾害损失、电力系统日负荷量、数据信号和抽样调查数据等周期性曲线处理[9-10]。此外,傅里叶级数拟合也可用于非周期性曲线的拟合[11],如凸轮升程曲线[12]。
本文以三电平NPC 为研究对象,采用傅里叶级数拟合法实现三电平SHEPWM 开关角轨迹曲线的拟合,并与常用的多项式曲线拟合法对比。最后,通过仿真及实验验证了傅里叶级数拟合法的可行性。
1 SHEPWM 基本原理
图1 为三电平NPC 逆变器三相拓扑,图2 为三电平NPC 逆变器的输出相电压波形。

图1 三电平NPC 逆变器拓扑Fig.1 Topology of three-level NPC inverter
SHEPWM 将三电平逆变器输出的相电压波形通过傅里叶级数展开,为消除特定次谐波而得到一组非线性方程组。通过求解非线性方程组,可得各个开关角度。
图2 中,a 相电压Ua的输出波形由傅里叶级数展开为

图2 三电平NPC 逆变器输出相电压波形Fig.2 Waveforms of output voltage of three-level NPC inverter

式中:n 为基波和各次谐波次数;ω 为角频率;t 为时间;qn和rn分别为相电压波形中正弦分量和余弦分量的幅值,分别表示为

图2 中:α1,α2,…,αN为开关角;N 表示开关角个数;Udc为直流侧总电压。输出相电压波形具有半波对称和1/4 周期对称的特点,因此输出波形所含的谐波成分中不存在偶次分量,可得

当输出侧接三相对称负载时,3 的倍数次谐波在线电压中相互抵消,只需考虑消除6k±1(k=1,2,…)次谐波,可得基波(即n=1)分量和n 次(n=6k±1,k=1,2,…)谐波分量的电压幅值分别为

取直流侧总电压Udc的一半即Udc/2 为基值进行标幺化,则式(5)可变为

式(6)中,N 个开关角构成含有N 个方程的非线性方程组,消除N-1 个特定次谐波,如N=7 时,消除5、7、11、13、17 和19 次谐波。
求解式(6)的非线性超越方程组,目前有遗传算法[7]、牛顿迭代法[13]、同伦迭代算法[14]、蚁群算法[15]等方法,本文采用牛顿迭代法进行求解。牛顿迭代法求解的关键是迭代初值的选取,因为迭代初值与解的收敛性有关。本文采用文献[13]中迭代初值的选取方法,得到开关角随调制比m 变化的轨迹曲线,如图3 所示。由图3 可知,在低调制比区,开关角与m 接近线性关系;在高调制比区,开关角轨迹变化较大。

图3 不同开关角个数下开关角度随调制比的分布Fig.3 Distribution of switching angle with variable modulation ratio under different numbers of switching angle
2 曲线拟合法
2.1 多项式曲线拟合法
多项式曲线拟合法广泛应用于曲线拟合。在开关角轨迹曲线拟合中,第i 个开关角αi的曲线拟合表达式为

式中:i=1,2,…,N;m 为调制比;pi0,pi1,…,pih为多项式拟合系数;h 为pih对应的拟合阶数,且h=1,2,…,g;g 为所选拟合阶数,g 越大,拟合曲线越逼近原曲线,拟合误差越小。当拟合曲线的波动过大时,即便g 增大,拟合误差依旧很大,则需采用分段拟合,以减小拟合误差。
鉴于多项式曲线拟合法在不分段的情况下,拟合曲线波动过大时拟合误差过大。为减小拟合误差需多次试验寻找分段点进行分段的缺点,本文提出采用傅里叶级数拟合法来拟合开关角曲线。
2.2 傅里叶级数拟合法
对于周期性曲线,傅里叶级数展开式为

式中:a0,a1,a2,…,aj和b1,b2,…,bj为傅里叶系数;x为ax和bx对应的拟合阶数,x=1,2,…,j;j 为选定的展开阶数。若j 选取过大,会增大计算量;若j 选取过小,则无法满足拟合精度的要求,所以需要选取适当的j 值。
采用傅里叶级数拟合法拟合开关角轨迹曲线时,傅里叶级数展开式为

式中:i=1,2,…,N;ωi为开关角αi曲线拟合时对应的角频率。
由于开关角轨迹曲线为非周期性曲线,可将其看作某个周期性曲线的某一部分进行傅里叶级数展开。在非周期性曲线中,ωi和傅里叶系数由非线性最小二乘法[16]计算得出。
计算ωi,ai0,ai1,ai2,…,aij,bi1,bi2,…,bij的具体实现过程如下。
定义向量

根据式(9),在全调制比范围内,将m 等份划分为λ 份,则λ 份mλ满足

当满足j≤λ/2 时,通过非线性最小二乘法计算Xi和ωi;若不满足j≤λ/2,则求解的未知数多于方程个数,无法求解Xi和ωi。
以N=7 的开关角轨迹为例,分别采用多项式曲线拟合法和傅里叶级数拟合法进行曲线拟合,在拟合精度为±1.5°下对比分析。曲线拟合情况如图4~图6 所示,其中图4(a)、图5(a)和图6(a)中实线为原轨迹曲线,虚线为拟合轨迹曲线。图4(a)和图5(a)中的第1 分段和第2 分段以及图5(a)中的第3分段表示分段拟合区域。
图4 为多项式曲线拟合法在全调制比范围内分2 段拟合,在m 为0~0.68 时5 阶多项式拟合;0.68~1.15 时6 阶多项式拟合。图5 为3 段4 阶多项式拟合,即m 分为0~0.68、0.68~0.849 以及0.849~1.15。图6 为傅里叶级数拟合法在全调制比范围内直接拟合,且为7 阶傅里叶级数展开。

图4 多项式曲线拟合法:2 分段Fig.4 Polynomial curve fitting method:2 segments

图5 多项式曲线拟合法:3 分段Fig.5 Polynomial curve fitting method:3 segments
对比图4 和图5 可知,多项式曲线拟合法分段越多,总体的拟合误差越小,但在保证拟合精度的条件下,需经过多次实验来选取满足拟合精度的分段点,并且不同开关角个数的拟合曲线所选取的分段点也不相同,因而实现较为繁杂。由图4~图6 对比可得,与多项式曲线拟合法相比,傅里叶级数拟合法无需分段,在全调制范围内可直接拟合,在不同的开关角个数下无需额外寻找分段点,实现较为简便。
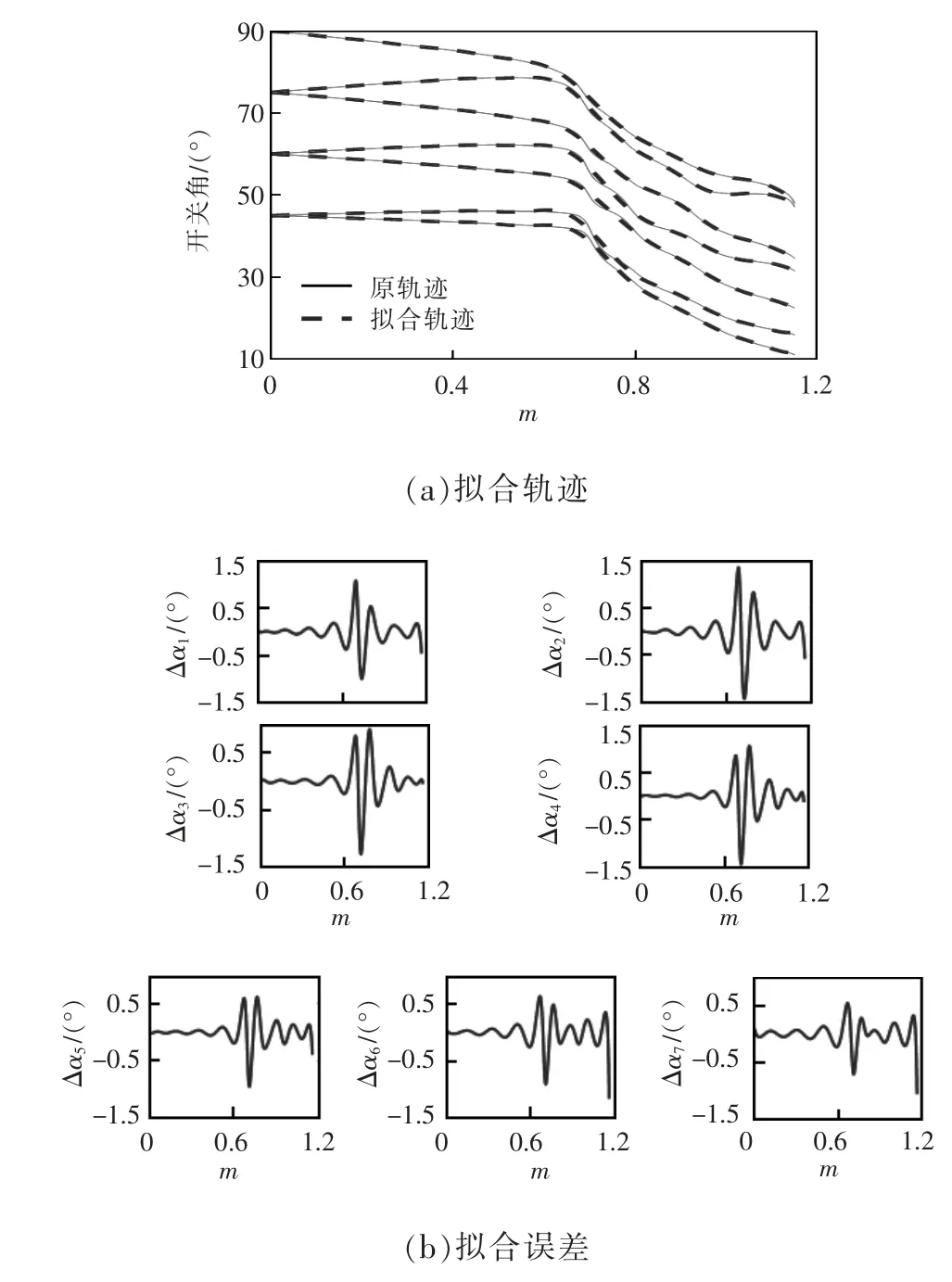
图6 傅里叶级数拟合法Fig.6 Fourier series fitting method
3 仿真分析
为验证傅里叶级数拟合法的可行性,在Matlab/Simulink 搭建三电平NPC 逆变器仿真模型,验证当开关角个数为7,即N=7 时,采用傅里叶级数拟合法和多项式曲线拟合法的消谐效果,并对比分析。仿真参数如表1 所示。

表1 仿真参数Tab.1 Simulation parameters
图7~图9 分别为不同拟合法下a 相输出电压Ua、ab 相线电压Uab、a 相输出电流Ia仿真波形及各自对应的谐波含量。对比可得,多项式曲线拟合法和傅里叶曲线拟合法基本消除3、5、7、11、13、17 和19 次谐波,并能达到目标的调制比0.8 左右。此外,两种方法的输出电流谐波含量基本一致。

图7 多项式曲线拟合法:2 分段(仿真)Fig.7 Polynomial curves fitting method:2 segments(simulation)

图8 多项式曲线拟合法:3 分段(仿真)Fig.8 Polynomial curve fitting method:3 segments(simulation)

图9 傅里叶级数拟合法(仿真)Fig.9 Fourier series fitting method(simulation)

4 实验验证
为验证傅里叶级数拟合法是否可行,搭建了以TMS320F28335 为核心芯片的三电平NPC 实验平台。实验参数与仿真参数一致。
图10~图12 分别为不同拟合法下的实验波形及对应的谐波分析。由图10~图12 中的实验波形与图7~图9 中的仿真波形对比可知,实验波形与仿真波形一致。图10~图12 中,3 种方式的相电压基波幅值都在78 V 左右,线电压基波幅值在133 V 左右,相电流基波幅值在2.2 A 左右,并且5、7、11、13、17和19 次谐波已基本被消除,因而3 种方式谐波消除效果基本一致,验证了傅里叶级数拟合法的有效性。由实验与仿真的谐波含量对比可见,谐波分布一致,但基波幅值偏小,谐波THD 偏大,这是由于实验中逆变器直流侧为不控整流提供的电压,非理想直流电压,故直流侧电压存在偏差和波动,导致基波幅值偏小,谐波THD 增大。

图10 多项式曲线拟合法:2 分段(实验)Fig.10 Polynomial curve fitting method:2 segments(experiment)

图11 多项式曲线拟合法:3 分段(实验)Fig.11 Polynomial curve fitting method:3 segments(experiment)

图12 傅里叶级数拟合法(实验)Fig.12 Fourier series fitting method(experiment)
表2 为实验过程中3 种方法的计算耗时。由表2可以看出,多项式曲线拟合法(3 分段)总的计算耗时最短,而傅里叶级数拟合法的计算耗时比较长,这是由于傅里叶级数拟合法中采用了三角函数,而三角函数的计算需要耗费一定的时间。但傅里叶级数拟合法在实现上比多项式曲线拟合法简便。
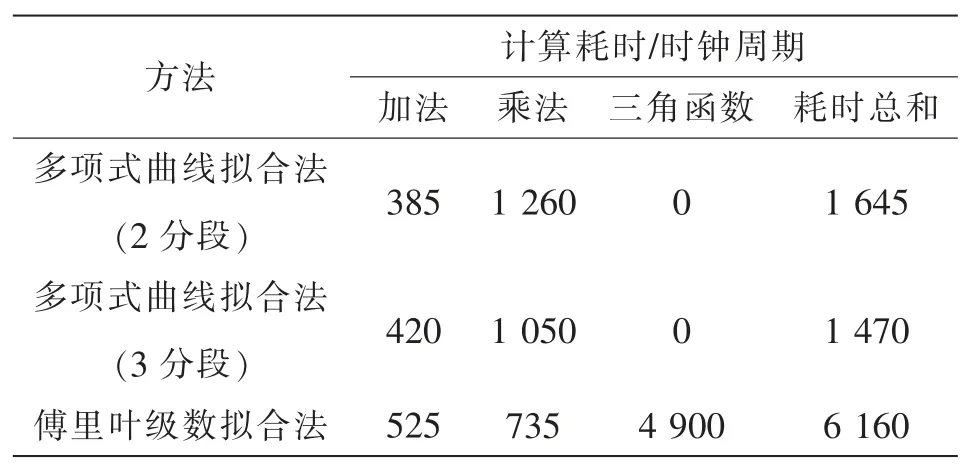
表2 实验计算耗时Tab.2 Time consumption in experimental calculations
5 结论
本文提出了采用傅里叶级数拟合实现三电平SHEPWM 开关角轨迹曲线拟合的方法,通过仿真和实验验证傅里叶级数拟合法的有效性。可以看出,傅里叶级数拟合法能在全调制比范围内进行曲线拟合,拟合曲线十分平滑;在满足拟合精度的情况下,比多项式曲线拟合法简便,且无需分段。
在实际工程中,采用傅里叶级数拟合法实现三电平SHEPWM 更为简便,为三电平及其他电平SHEPWM 的实现提供了一种新的方案。

