多电平变换器PWM 控制技术研究现状综述及最新进展
朱 宏,李永东,王 奎,QAMAR Muhammad Attique,徐晓娜
(清华大学电机系电力系统及发电设备控制和仿真国家重点实验室,北京 100084)
多电平变换器因具有可使用低耐压的器件实现高压大功率输出、输出电压谐波较少[1]、无需变压器的特点,近年来在大容量功率转换领域得到了越来越广泛地研究和应用。而多电平脉宽调制PWM(pulse width modulation)控制方法是多电平变换器研究领域的核心问题之一。原则上讲,基于传统两电平逆变器的PWM 控制方法,都可以推广到多电平逆变器中,目前多电平PWM 方法主要包括载波PWM 和空间矢量脉宽调制SVPWM(space vector pulse width modulation)。由于PWM 控制方法和拓扑是紧密联系的,而多电平变换器拓扑结构灵活多变,不同的拓扑有不同的特点和要求,因此不断优化现有PWM 控制方法以满足不同拓扑的控制要求和性能指标,成为多电平功率变换器PWM 控制策略中一个非常重要的研究内容[2-3]。
一般可以将现有的各种多电平PWM 控制方法按照调制方法的不同分为两大类,分别是载波PWM和SVPWM 控制方法。载波PWM 控制方法是通过载波和调制波的比较,得到开关脉宽控制信号;SVPWM 控制方法则是通过查表得出参考电压矢量所对应的开关状态时序,从而得到对应的脉冲信号。此外,多电平变换器主要分为3 大类:二极管箝位多电平变换器[4]、飞跨电容变换器[5]以及级联H 桥多电平变换器[6],针对不同的多电平变换器,多电平PWM控制方法有不同的控制目标和性能指标,但归纳起来,PWM 技术的研究内容主要包括电容电压平衡控制[7-8]、输出谐波控制[9]、直流电压利用率和器件开关损耗控制[10]等。此外,载波PWM 和SVPWM 在一定条件下存在内在联系。
1 载波PWM
1.1 载波PWM 的基本算法
多电平载波PWM 是两电平载波PWM 的直接推广应用,由于多电平变换器有多个载波,根据载波之间的关系可以分为3 种基本调制方法:载波层叠PWM、载波移相PWM 及载波交叠PWM。
1.1.1 载波层叠PWM 和载波移相PWM
载波层叠PWM 及载波移相PWM 调制示意如图1 所示。根据三角载波之间相位关系的排列不同,载波层叠PWM 可分为3 种不同的多电平载波比较PWM 方法,分别为:同相层叠PD(phase disposition)方式、正负反相层叠POD(phase opposition disposition)方式和交替反相层叠APOD(alternative phase opposition disposition)方式。
以同相层叠方式为例,对比两电平和三电平变换器下的输出波形,其波形与谐波分析分别如图2和图3 所示。可见,当电平增加,输出谐波降低。

图2 两电平变换器输出波形Fig.2 Output waveform of two-level converter

图3 三电平变换器输出波形Fig.3 Output waveform of three-level converter
多电平载波移相PS(phase-shift)PWM 是指,对于一个n 电平变换器,采用n-1 个不同相位的三角载波与调制波比较,每个载波依次移相360°/(n-1),其PWM 波形如图1(d)所示。载波移相PWM 和载波层叠PWM 在输出谐波方面有所不同,由双边傅里叶分析可得以下结论。

图1 载波层叠PWM 及载波移相PWM 示意Fig.1 Schematic of carrier disposition PWM and carrier phase-shift PWM
(1)载波同相层叠法的谐波性能最好,尤其是线电压谐波性能。交替反相层叠法次之,正负反相层叠式效果最差。
(2)APOD 和PS 方式有相同的谐波性能,前提是在一个基波周期内总的开关次数相同。
(3)在PS 方式下,通过不连续的控制波与移相载波的比较,可以得到类似PD 方式的谐波性能。
1.1.2 载波交叠PWM
在载波层叠PWM 的基础上,还有特定谐波消除PWM[11]和载波带频率变化PWM[12]方法,前者可以降低输出谐波含量,后者可平衡器件开关次数,提高器件使用寿命,但这2 种方法都存在低调制度下电平退化的问题,即低调制比时,存在一些开关器件始终处于开通或关断的状态[13],开关管得不到完全的利用,而载波交叠CO(carrier-overlapping)PWM 可以提高开关管的利用率。
载波交叠PWM(COPWM)是基于多电平变换器载波之间在竖直方向的位移和水平位移这2 个自由度,提出的新型PWM 方法,目前该方法主要分为3 类,其调制波形如图4 所示。其中,COPWMA 调制方法输出的线电压,无论是谐波频谱还是谐波含量,都是3 种方法中最好的;COPWM-B 次之;COPWM-C 最差。载波交叠PWM 在低调制度下具有良好的谐波性能,在高调制度下与特定谐波消除PWM 方法基本相同[3]。
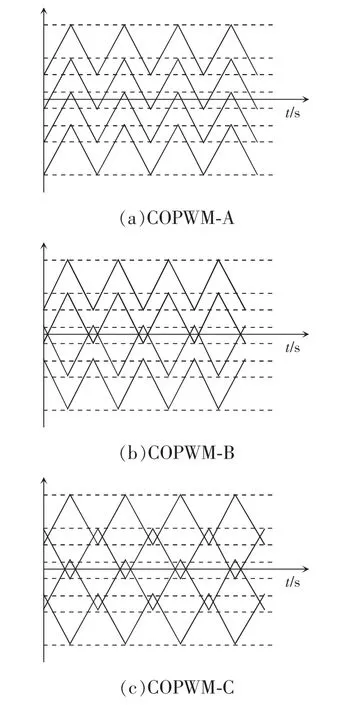
图4 五电平变换器载波交叠PWMFig.4 Carrier-overlapping PWM of five-level converter
1.2 载波PWM 性能指标的优化
1.2.1 输出谐波性能
1973 年美国学者Patle H S 和Hoft R G 首次提出特定消谐脉冲宽度调制法,通过对输出电压的波形进行快速傅里叶变换FFT(fast Fourier transform)分析,得出特定条件下傅里叶展开式,令某些特定次数的谐波为0,得到一个非线性方程组,求解这个方程组,得到开关角,将最终求出的开关角应用于逆变器的控制,则可以在输出电压中消除所对应开关角的低次谐波[14]。特定谐波消除法是常用的一种谐波控制方法,但由于需要对非线性方程组求解,计算较为复杂[15],目前对该方法的研究主要围绕对求解过程的优化。文献[16]对载波形状进行了改进,令每个基波周期内60°~120°,240°~300°之间的载波幅值为0,从而降低了开关频率,改善了谐波特性。
1.2.2 直流电压利用率
载波移相PWM 控制方法已成为H 桥多电平电路的标准PWM 控制方法,但载波移相PWM 控制为避免发生过调制,使得输出电压幅值较小[17]。针对这个问题,文献[18]将三次谐波注入法与载波移相结合起来,应用到级联H 桥型多电平逆变器的控制中,既能拥有良好的谐波抑制特性又能保持较高的直流电压利用率。载波PWM 控制法在实际应用中加入死区后会引起电流波形畸变,降低电压利用率,为此文献[19]提出了一种应用于三电平逆变器的无死区载波层叠PWM 法,采用三重载波生成PWM 信号,通过分析不同工作状态时的死区效应,推导出功率开关管的导通和关断规律,根据电压极性和电流方向确定不同工作状态下的驱动信号逻辑,实现无死区控制。除此之外,还有开关频率优化PWM,对于无中线的三相对称负载系统,在三相逆变器输出电压中加入3 的倍数次谐波或直流分量时,对负载电压波形不会产生影响,利用加入的不同零序分量可以实现载波调制的不同优化目标,如控制电容电压平衡[20]、提高电压利用率[21]及降低开关损耗等[22]。
1.2.3 电容电压平衡控制
为实现飞跨电容型逆变器的电容电压平衡,文献[23]提出了一种新型载波同相层叠PWM,该方法利用了飞跨电容型多电平逆变器开关状态冗余的特点,增加零电平选择环节,灵活控制零电平向量,实现了三电平飞跨电容逆变器的电容电压平衡,同时具有载波同相层叠方法的各项谐波性能。文献[24]提出了一种改进的载波交叠PWM,该方法中每个载波带中包含所有开关对应的载波,可以实现飞跨电容电压平衡,且可推广到N 电平逆变器。文献[25]为解决四电平中点箝位型变换器的中点电压平衡问题,提出了一种新型的载波交叠PWM,该方法可在全调制指数和功率因数范围内实现中点电压平衡,其载波波形如图5 所示,其中Cr1、Cr2、Cr3为相位相同,幅值不同的三角载波。该调制方法下的3个母线电容电压的偏移量分别为ΔUd1x、ΔUd2x和ΔUd3x,其表达式为
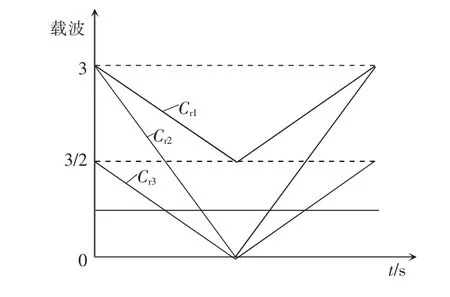
图5 改进载波交叠PWMFig.5 Improved carrier-overlapping PWM

2 SVPWM
SVPWM 易于数字化实现,特别是多电平SVPWM 技术具有直流电压利用率高、开关损耗低等优点,在开环和闭环控制系统中都得到广泛应用。
2.1 SVPWM 的基本控制方法
该类方法是从两电平SVPWM 直接推广而来的。SVPWM 算法的基本原理就是基本电压矢量在一定的时间作用下合成得到输出电压矢量,用多边形无限逼近于圆,从而使电机获得幅值恒定的圆形磁场,即正弦磁通[26]。在控制过程中,需要先判断参考电压矢量所在位置,根据最近三矢量法选择基本电压矢量,并根据伏秒平衡原理计算各矢量作用时间,然后根据基本矢量与开关状态的对应关系,并结合其他要求,确定所有输出的开关序列及其输出形式。但是,随着电平数的增多,可选择的多电平空间矢量也很多,同时由于在直角坐标系下需要求解三角函数,计算量较大。
2.2 SVPWM 控制的优化
2.2.1 非正交坐标系下的SVPWM 算法
非正交坐标系包括g-h 坐标系(60°坐标系)和K-L 坐标系(120°坐标系)。g-h 坐标系和K-L 坐标系的三电平空间矢量如图6 所示[27]。

图6 g-h 坐标系和K-L 坐标系下三电平空间矢量Fig.6 Three-level space vector in g-h and K-L coordinate systems
非正交坐标系下SVPWM 算法的具体实现步骤如下。
步骤1选择合成电压矢量。以K-L 坐标系为例,设参考电压为Vref,VrL、VrK为Vref在K-L 坐标系下的分量。分别对VrL、VrK向上取整和向下取整得到4 个坐标,在坐标轴上的位置如图7 所示。
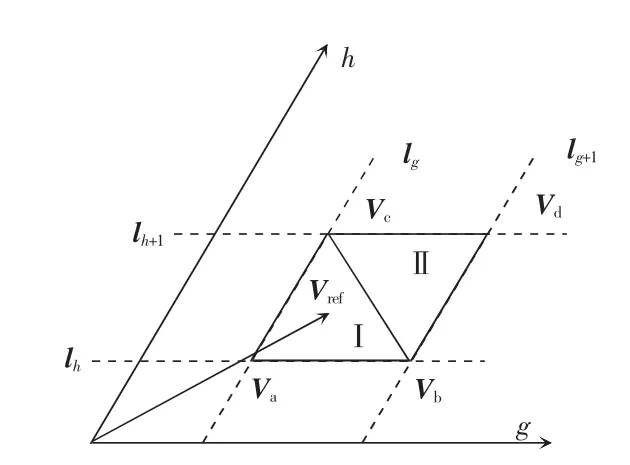
图7 合成电压矢量位置示意Fig.7 Schematic of composite voltage vector position
步骤2根据Vref所在区域,选择最近的3 个电压矢量。判断其所在区的数学表达式为

式中:K=int(VrK);L=int(VrL)。
步骤3计算矢量作用时间。设Vref在Ⅰ区,则选择的基本矢量为Va、Vb、Vc,由伏秒平衡可得各矢量作用时间为

式中,Ta、Tb、Tc为基本矢量Va、Vb、Vc的作用时间。
步骤4确定输出开关状态。三相开关的输出状态为

可根据不同的控制目标选择开关状态。
文献[28]提出了一种采用平面三相虚坐标的方法实现多电平PWM 控制的通用算法,将SVPWM 控制分为输出电压合成和通过零序电压进行控制两方面,其中ja、jb、jc为虚坐标轴,由a、b、c 轴逆时针旋转90°可得。一方面体现了三相对称的特点,便于数学分析;另一方面计算方便,能适用于不同拓扑的各种应用场合。除此之外,为满足三相四线制四桥臂逆变器的控制需求,产生了三维空间坐标系下的SVPWM 控制算法,将空间矢量的三相定义扩展为“四相”,将第4 相的零线输出放在与原有平面垂直的轴上,从而构成了“三维”PWM 方式[29]。
2.2.2 电容电压控制
空间矢量图中包括长矢量、中矢量、小矢量和零矢量,其中中矢量和小矢量作用时的输出电流会造成中点电压偏移,当工作条件涉及较大的调制指标和有源负载电流时,传统的SVPWM 无法实现具有较多电平(N>3)的中点箝位型变换器的电压平衡。为此,文献[30]提出了一种虚拟矢量合成的方法,在理论和实验中证明了此方法既可以实现中点电压平衡控制,又避免了较高的dv/dt,在空间矢量的基础上定义了以下2种虚拟矢量。
(1)虚拟中矢量。中矢量的输出电流会造成中点电压偏移,将1 个中矢量和2 个小矢量合成为虚拟中矢量,3 个矢量输出电流分别为ia、ib、ic。令每个矢量的作用时间相等,则io=ia+ib+ic=0,虚拟中矢量对中点电压无影响,因此在理论上可以完全控制中点电压平衡。
(2)虚拟长矢量。虚拟长矢量由1 个长矢量和2个短矢量合成,2 个短矢量的占空比相等且小于长矢量的占空比,故虚拟长矢量对中点电压无影响,且dv/dt 更小。
在此基础上,文献[31]提出了最近三虚拟空间矢量PWM,并给出了新的虚拟矢量定义方法及选择标准,合成原则为
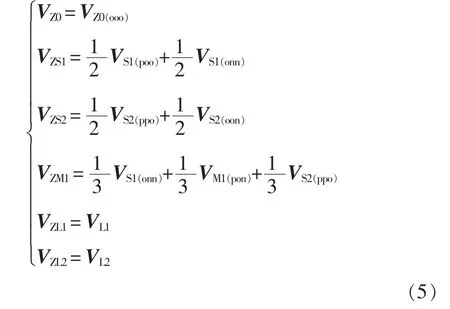
式中:矢量VZ0、VS1、VS2、VZM1、VZL1、VZL2均为虚拟空间矢量;VZ0、VS1、VS2、VM1、VL1、VL2为基本 电压矢量;p、o、n 分别表示三相输出电平为Vdc/2、0、-Vdc/2。各虚拟矢量在一个采样周期内输出的中点电流的有效值为0,故各虚拟矢量对中点电压无影响,不会造成中点电压波动。
虚拟矢量控制在理论上可以实现对中点电压平衡的完全控制,但在实际应用中,在计算误差及干扰下,由于累计效果,可能造成中点电压波动。针对这个问题,文献[32]基于三电平中点箝位型变换器,提出了一种变虚拟空间矢量,对虚拟小矢量引入调节因子,通过检测中点电压波动情况,调整下一周期虚拟矢量的作用时间,从而弥补上一周期的中点电压偏差量,实现中点电压平衡控制。
采用传统虚拟空间矢量PWM 理论上可以实现直流电容电压平衡的全控制,但增加了计算量和复杂度。四电平NPC 变换器采用空间矢量PWM 时,每个扇区包含9 个三角形,而虚拟空间矢量PWM将一个扇区的三角形数增加到13 个,这将增加计算量和实现的复杂度。此外,其增加了开关频率,恶化了逆变器的输出波形。
为实现四电平二极管箝位变换器的中点电压平衡,同时减少计算量,文献[33]提出了一种简化虚拟空间矢量PWM,该法可将四电平空间矢量图简化为三电平空间矢量图。对虚拟矢量的定义为

通过对传统虚拟矢量进行合成再定义,四电平空间矢量得到了很大简化,每个扇区仅有4 个三角形,大大简化了运算量,降低了算法的复杂度。
四电平简化虚拟空间矢量算法已在实验中得到验证,图8 为调制比m=0.9 时四电平箝位型变换器在该算法下的相电压、线电压、相电流及电容电压的波形。

图8 m=0.9 时四电平NPC 简化虚拟空间矢量下的波形Fig.8 Waveforms of four-level NPC simplified virtual space vector when m=0.9
3 SVPWM 与载波PWM 统一理论
由于SVPWM 和载波PWM 均为基于一个采样周期内电压积分等效的思路,故二者在本质上是等效的。文献[34]以二极管钳位型五电平逆变器为例,采用调制波分解策略,在常规的三角载波PWM 的各相调制波中加入一个零序分量就可得到和SVPWM 完全相同的输出波形,从而推导出任意电平8 段以上SVPWM 开关序列与载波PWM 的统一理论。以该方法为基础,文献[35-36]分别对飞跨电容型变换器和有源中点箝位变换器,提出了改进的调制波分解方法,完善了不同拓扑结构下的SVPWM 与SPWM 的统一理论,在此基础上,系列结合SPWM 与SVPWM 优点的优化PWM 算法被提了出来。
文献[37-38]利用SVPWM 与载波PWM 的联系,提出了一种基于载波SPWM 与SVPWM 混合控制的三电平逆变器中点电位平衡策略,实现了不同负载功率因数变化下的中点电压平衡。文献[39]以SPWM对称规则采样的波形与SVPWM 对称七段式波形相似为出发点,由SPWM 的调制隐函数推导出SVPWM 的调制隐函数,并对SVPWM 的调制隐函数进行简化分解,得出简化的SVPWM 算法,该算法直接利用三相参考电压瞬时值计算PWM 信号的开关状态切换时间,不需进行坐标变换、三角函数运算、扇区判断和有效矢量作用时间的计算。
通过理论分析,SVPWM 可通过向SPWM 注入特殊零序分量得到,二者在本质上是一致的,只是在实现方法上有所不同。
4 结语
本文主要介绍了多电平载波PWM 和SVPWM控制方法,在此基础上,针对不同拓扑结构、不同控制目标,介绍了多种优化控制方法。多电平变换器具有广泛的应用前景,电平数不断增加,多电平变换器的拓扑结构也在不断地优化,多电平PWM 算法的优化目标和计算量随之增加,而多电平SVPWM 与SPWM 统一理论的提出,可对算法进行一定的简化,后续可在该理论的基础上进一步研究2 种PWM 方法数字实现的统一,将SPWM 实现简单和SVPWM 易数字化的优点结合起来。

