圆锥曲线参数范围类题型求解策略

韦 能

(广西钦州市第二中学 535099)

围绕圆锥曲线参数范围求解目标，结合常见参数范围求解题型，本文从不等关系建立角度出发，将此类题型细分为四大类：题设条件类不等关系、圆锥曲线位置不等关系、圆锥曲线范围类不等关系、基本判别式类不等关系.通过对上述四类圆锥曲线参数类题型求解的典型案例分析，从解题技巧上帮助学生掌握求解方法，从而实现灵活应用.

一、利用题设条件建立不等关系

利用题设条件求解圆锥曲线参数范围类题型属于较为直接和基础类的题型，通过对题设条件中已有的不等关系进行直接应用，正向构建含参不等关系.在此类题型的求解过程中，需要紧密关注对应圆锥曲线的类型及取值范围，并结合圆锥曲线的定义判定范围.

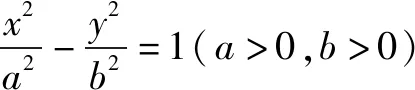
点评利用题设条件建立不等式，求解圆锥曲线不等关系类题型属于直接正向求解思维的应用.在实际求解过程中，切忌疏忽大意，必须紧密留意圆锥曲线自身的范围，避免多解问题的出现.

二、利用位置关系建立不等关系

在圆锥曲线中利用位置关系建立不等式，需要深入挖掘潜在信息，建立圆锥曲线相关的目标函数与参数之间的不等关系，才能实现此类题型的求解.

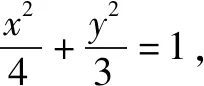
解析设两点A(x1,y1)、B(x2,y2)为椭圆C上关于直线l对称的两点，点M(x,y)为弦AB的中点.由于点A、B均在椭圆C上，故可知3x1+4y1=12、3x2+4y2=12，

联立两式得到关系式

3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0

简化后得到

结合点M与点A、B之间的位置关系可知，

x1+x2=2x、y1+y2=2y，

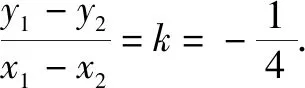
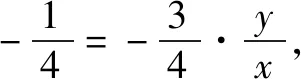
即是3x-y=0,再与y=4x+m

联立方程组得到交点M(-m,-3m).由于点M在椭圆内，得到

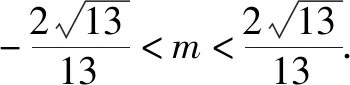
点评圆锥曲线位置关系类不等关系题型的求解，可以概括为先将已知条件中涉及的基本量转化为圆锥曲线位置关系，本题再利用点与圆锥曲线的位置关系：点在圆锥曲线内、圆锥曲线上及圆锥曲线外，得到不等关系，进而判定参数范围，顺利实现求解.

三、利用曲线范围建立不等关系

圆锥曲线自身范围具备多种特征，针对椭圆、双曲线等圆锥曲线，其定义域、值域、焦点、准线等等，都是此类题型常用的位置关系，求解此类题型的关键在于建立参数与曲线位置之间的不等关系.

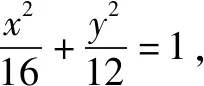
解析设点P(x,y)，由于点P位椭圆上的动点，故有-4≤x≤4.

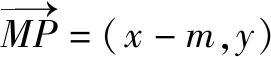
化简后得到

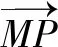
结合-4≤x≤4,最终可知m≥1.

点评利用圆锥曲线范围建立不等关系求解参数范围时，关键在于对圆锥曲线几何特征的应用，这就要求学生必须熟练掌握圆锥曲线的基本特性，尤其是位置关系与函数表达式之间的转化，只有建立相关联系后才能准确判定参数范围.

四、利用判别式建立不等关系

利用判别式确定不等关系类题型常出现于直线与圆锥曲线相交的题型中，通过直线方程与圆锥曲线方程联立方程组，进而得到一元二次方程，最后结合判别式中所含有的参数不等式进行求解.

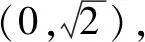
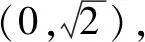
再将直线l的表达式带入椭圆C的表达式，得到

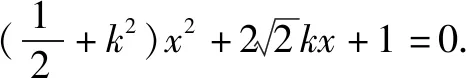
此时利用判别式定理得到

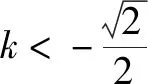
点评当题中已知条件为直线与圆锥曲线之间的位置关系时，此时容易联想到联立直线与圆锥曲线之间的方程组，最终得到一个一元二次方程形式的含参表达式，结合判别式或基本不等式即可实现求解.

总之，求解圆锥曲线参数范围类题型，最关键之处在于不等式关系的建立，再结合已知条件，利用圆锥曲线性质、几何特征、判别式或基本不等式等方式，从而构建含参不等关系，最终实现参数范围的判定.