2021年1月八省联考导数题的解法探析

彭耿铃

(福建省泉州市第七中学 362000)

2021年1月八省联考的导数压轴题在形式上有“简约而不简单”之感，大多数考生不知所措.本文旨在探究此类题型规律，揭示解题方法，提供解题规律，希望读者能决胜于高考.

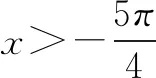
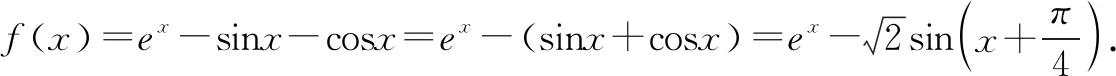
解法二(从不同角度合理分类)：f′(x)=ex-cosx+sinx；

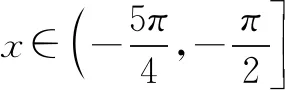
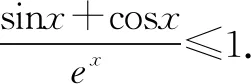
综上所述，φ(x)≤1，即f(x)≥0.

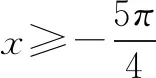
综上所述，若g(x)≥2+ax，则a=2.

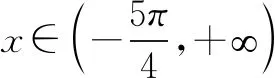
①若a>2，k(0)<0，k(lna+1)>0，故存在唯一x0∈(0,lna+1)，使得k(x0)=0.当x∈(0,x0)，k(x)<0，g(x)-ax-2单调递减，而g(0)-a×0-2=0，故g(x0)-ax0-2<0；

②若00，k(-π)<0，故存在唯一x1∈(-π,0)，使得k(x1)=0.当x∈(x1,0)，k(x)>0，g(x)-ax-2单调递增，而g(0)-a×0-2=0，故g(x1)-ax1-2<0；

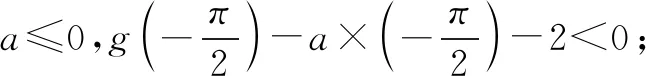
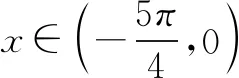
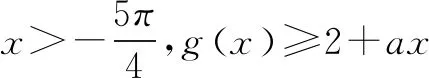
解法四(分离参数法+洛必达法则)：

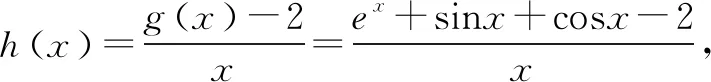
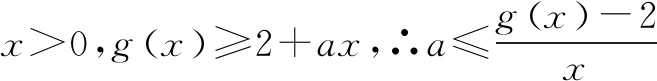
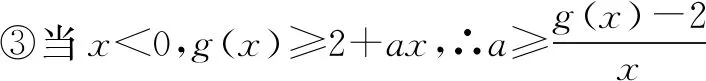
接下来验证a=2时，g(x)≥2+ax恒成立.(证明方法同解法一).

解法五(分离参数法+导数定义法(避开洛必达法则))：由g(x)≥2+ax，则ex+sinx+cosx≥2+ax，即ax≤ex+sinx+cosx-2.

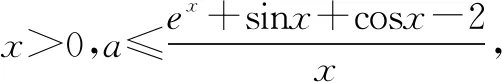
综上，a=2.

以上的几种证明方法更容易接近问题的本质，使得解题思维更加流畅，学生更容易接受，更容易地寻找解题的方向.因此我们教师在日常的教学中，应引导学生多视角思考，引导学生经历用不同方法解决数学问题，才能有利于学生开拓数学视野，为学生的终生发展、持续发展、多元发展奠定良好的基础.