淡化程式化套路 提升数学思维品质——以极坐标与参数方程复习为例

谢维勇

(四川省眉山中学校 620010)

《极坐标与参数方程》作为高考数学全国卷选考内容，阅卷显示全国多数学生选做此题.本部分内容题目的难度一般中等偏易，是学生的一个重要得分点，但学生完成情况欠佳，不少教师对内容的理解和处理上也存在一些偏差，简单训练学生将问题化为解析几何的程式化套路，经常被一些触及知识本质的问题区分，如何通过具体问题培养学生思维灵活性、深刻性、合理性等品质，更高效的做好本部分的复习值得思考.

在教学过程中，不少师生存在一个误区，认为此题有明确的套路，先将极坐标方程化为直角坐标方程，然后转化为直线、圆、圆锥曲线的位置关系求解即可.普通方程与参数方程是在平面直角坐标系下动点轨迹方程的两种不同表示形式，而参数方程最大的优点是能将曲线上任一点坐标用一个参数表示，变元只有一个，在求最值和设点等问题中减少未知量，极大简化运算.极坐标方程与直角坐标方程是在不同坐标系下曲线轨迹方程的表达形式，在两点间的关系用夹角和距离很容易表示时，极坐标系更具优势；而在平面直角坐标系中，这样的关系就只能使用三角函数来表示.对于很多类型的曲线，极坐标方程是最简单的表达形式，甚至对于某些曲线来说，只有极坐标方程能够表示.教材引进极坐标方程，是让学生了解不同表现形式在解决问题时的优势和局限性，而不是变成极坐标与直角坐标简单互化的程式化套路.在教学中教师应着力引导学生从两种方程形式的优缺点上思考，采取更简练的方式解决问题，提升学生的数学思维品质.

笔者在复习解析几何板块的内容时，有意识的引导学生从极坐标与参数方程的角度思考问题，很多问题的解答得到了极大简化，下面呈现在教学中对近年的部分考题的分析与解答，希望能起到抛砖引玉的作用.

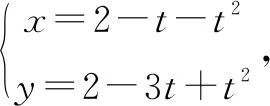
(1)求|AB|；

(2)以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求直线AB的极坐标方程.

分析本题检测学生对参数方程本质的理解，曲线上任意一点的坐标x,y都是变量t的函数，由方程思想，只要知道x,y,t中任意一个数的值便可计算其余两个数的值，问题迎刃而解.很多学生不假思索地希望将参数方程化为普通方程，再求其与坐标轴的交点，直接就走入了运算的死胡同.

解析(1)设A(0,y1),B(x2,0)

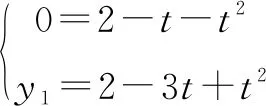
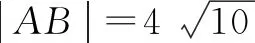
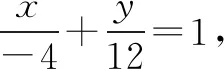
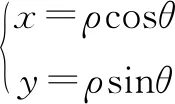
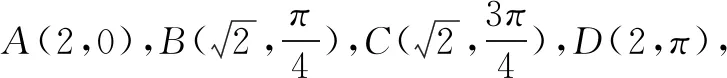
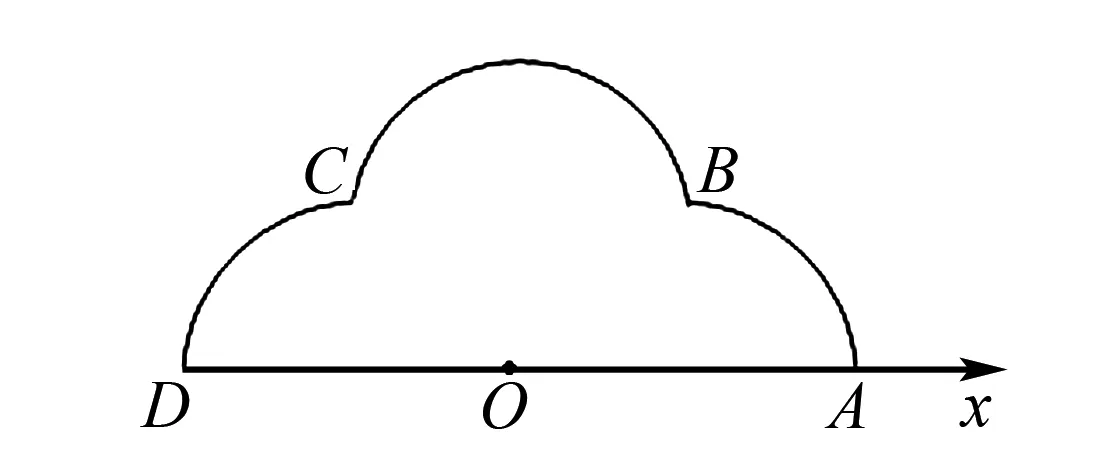
图1

(1)分别写出M1，M2，M3的极坐标方程；

分析本题一反常态，直接检测学生对极坐标方程的理解及应用，借助图形结合圆的定义建立曲线上动点极径与极角的等量关系是解决问题关键.

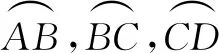
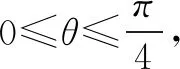
例3(2014年北京高考)已知椭圆C:x2+2y2=4.

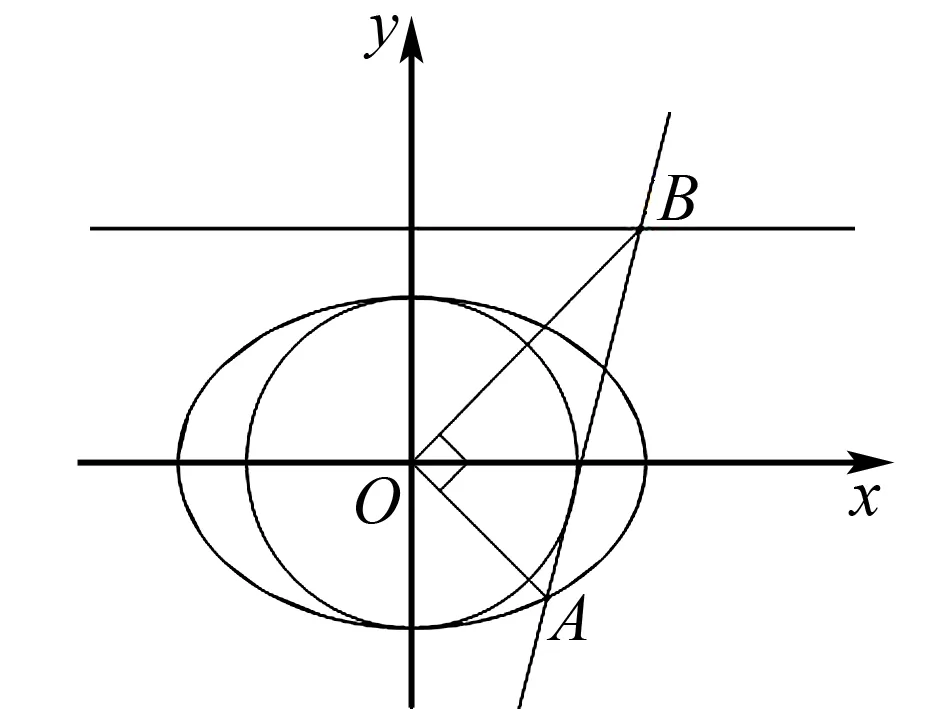
图2

(1)求椭圆C的离心率；

(2)设O为原点，若点A在椭圆上，点B在直线y=2上，且OA⊥OB，试判断直线AB与圆x2+y2=2的位置关系，并证明你的结论.

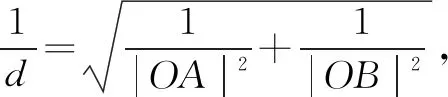
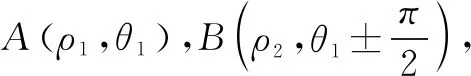
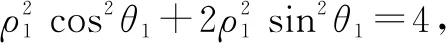
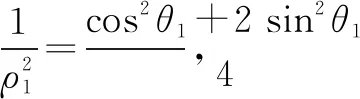
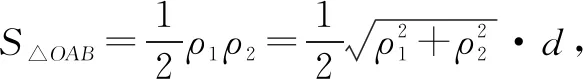
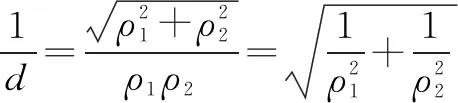
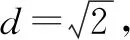
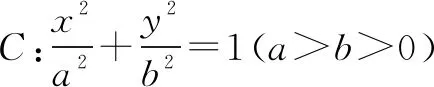
(1)求椭圆C的标准方程；

(2)若动点P(x0,y0)为椭圆C外一点，且点P到椭圆C的两条切线互相垂直，求点P的轨迹方程.

分析第(2)问从同一点作两条互相垂直的直线，考虑使用直线的参数方程，两直线结构相似，利用垂直关系，可用同一倾斜角表示，然后用交轨法整体消元能极大简化运算，凸显参数方程的优势.

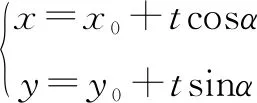
由△=0得

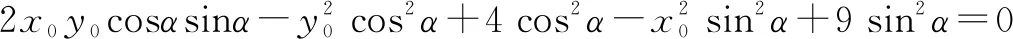
同理可得

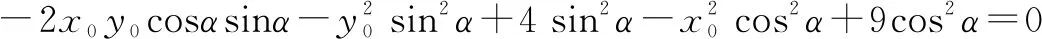
例5已知抛物线C:y2=2x的焦点为F，平行于x轴的两条直线l1,l2分别交抛物线C于A,B两点，交C的准线于P,Q两点，若点F在线段AB上，R是PQ的中点，求证：AR∥FQ.

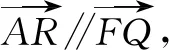
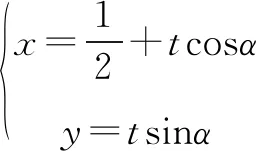
将直线AB与抛物线C:y2=2x

联立得：sin2α·t2-2cosα·t-1=0,

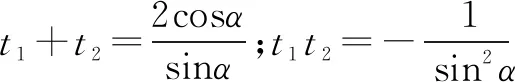
∴FQ∥AR

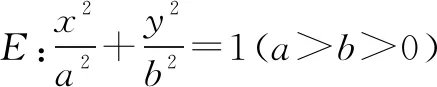
(1)求椭圆E的方程；

分析此题要证明的结论中，出现了A,B,C,D四个点到M的距离，M,C,D三点共线，M,A,B三点共线，过点M设出参数方程，结合kAB+kCD=0，将能用相同的变量θ,x0,y0表示，可以极大简化运算.

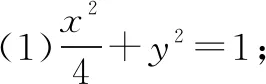
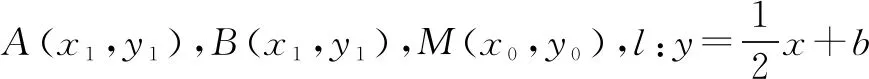
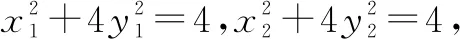
两式相减得

(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,

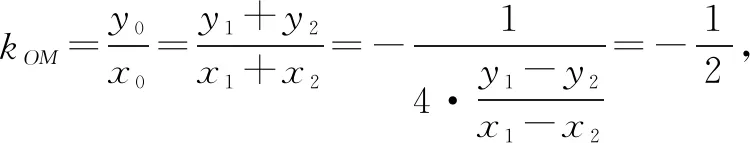
即kAB+kCD=0.

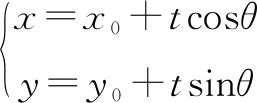
设该方程的两根为t1,t2

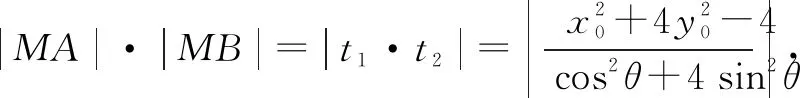
对于直线CD，将θ换为π-θ，同理可得

故|MA|·|MB|=|MC|·|MD|.

数学是思维的学科，教材是知识的载体，知识是思想方法的载体，教师在教学中只有借助知识引导学生领悟背后的思想方法，才能真正提升学生的数学思维品质，发展学生的核心素养，提高课堂的教学效率.