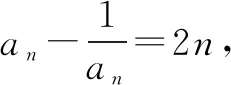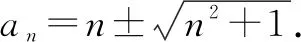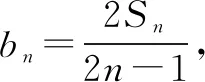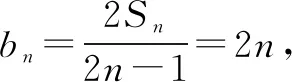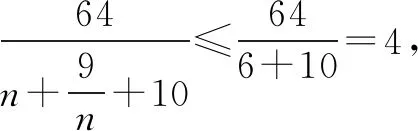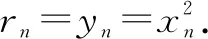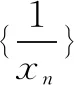高考数学数列问题解答策略

王继山

(辽宁省葫芦岛市第一高级中学 125100)

高考数学的试题每年都不一样，但所谓“换汤不换药”，通过对近些年数学的考题总结，就会发现大部分问题的解答时，在切入点、方法上的突破存有相应的相通性.根据数列的相关知识，就能牵扯到对于数列的递推公式对相关内容的考查，经过对高考数学的试卷可知，其不仅是考试热点，而且还是重点与难点的考察，因此学生必需充分掌握有关知识的同时，还应注意解题思维以及能力的提高，从而确保数列问题的解题正确率以及效率得到显著提高.在近些年的高考数学的试题当中，数列通常和函数、不等式、几何等相关知识相结合进行考查，该考查方式不仅增加了试题难度，而且对考生解题能力也具有更高要求，甚至上升到理性思维.

一、高考数列题解题方法的意义

高中数学中的数列知识不仅是高中时期极其重要的一种数学知识，而且还为学生在后期的数学知识学习奠定夯实的基础.就数列的内容分支及其构成结构视角分析，数列中的知识通常有着较强的发展性以及基础性，并能够与数学领域的其他知识实现有效结合，并形成崭新知识点考查学生学习的相关知识点.例如，数列通过会和函数、不等式、解析几何等相关内容相结合进行出题，这种教学，除了上文所讲解的问题外，数列题还能与学生的具体生活相联系，通过实际案例，对高中数学当中的相关数列问题实施分析，从而使学生自身的高考成绩得以显著提高的同时，促使学生呈现出强劲化的数学应用力.

二、高考数列的考点分类

根据对高考数学的数列试题实施分析之后，会发现的问题就是数列部分通常占据较大的分值，且在高考的许多压轴题当中都涉及到数列的相关知识.立足于数列考点分析，等差、等比等相关概念的通项公式及在具体问题当中的运用，都能使学生在具体学习当中，深入的认识到相关知识，对于数列的相关概念、表达方式等，学生具备初步认知即可.通过对高考数学的真题考查状况实施分析，大部分省份的高考对于数列相关知识的考核都会通过一道大题以及小题有效结合的形式，只有少部分省份的高考仅通过一道小题对数列知识实施考查，但是，仅通过一道小题考查的相关知识点仍旧比较全面，通过对数列的相关考题内容实施统计后，就能发现通项公式的相关知识考核难度为中等偏上，考核形式通常是在已知的递推关系上，把运用通项公式所推导得出的已知第n项和第n+1项的关系，将通项公式所推导的已知数列中的几项关系后，以通项公式实施推导，对数列的前n项和实施考查，其通常是学生对于数列的求和方法所掌握的状况实施考查，这通常是高考数学当中较为常见的考查方法.对于数列性质的相关知识而言，对其实施考查的难度通常位于中等水平，最常运用在选择题、填空题当中，其考查的内容也主要包含了等差数列当中项的性质、等比数列当中项的性质、数列单调性等.对于数列与函数的有效结合问题，其在高考当中已经出现了多次，但是，考试的题目通常难度比较大，数列与不等式相结合的问题通常会出现在压轴题中，其出现于高考当中，通常涉及到不等式及数列性质，其占据的分值比较大，且难度也比较大.

三、高考数学数列问题解答策略

1.数列和函数综合考查

数列部分的相关知识作为高考数学题当中所考查的主要内容，其和函数相结合逐渐成了近些年高考考查当中的命题热点.从本质上讲，数列也属于函数的重要表现形式，其作为自变量，属于正整数函数的一种呈现方式.对于数列而言，其作为特殊函数，所涉及到的问题解答的方式方法，都需学生通过函数思想进行分析，并对函数问题具备的作用以及学生应用函数思维进行解决的相关内容实施重点考查.

例如，已知函数f(x)=log2x-logx2(0

评析本题在设计结构时，通常比较灵活且巧妙，将函数作为切入，与数列和函数的有关内容相结合，对学生自身的逻辑分析能力实施系统考查，并在对数列相关问题解答的时候，注重对于方程以及函数的全方位检测.

2.数列和不等式综合考查

数列和不等式有效结合已成为近些年高考数学当中比较常见的考查方式.就一般数列的相关知识点来说，和不等式有效结合，不仅能增强学生自身的推理能力，而且在设计题型的时候，与函数类的题型相比也更加灵活，并深层次的考查了学生对于数列问题的解答，从而实现了在解答具体数列问题时，对学生综合运用所学知识的意识.

例如，已有等差数列{an}前n项和是Sn，其中a1=1，公差d≠0，同时，a1、a2、a7形成了等比数列.

(1)求取数列{an}的前n项和Sn.

解析(1)因为a1、a2、a7为等比数列，所以，a22=a1·a7，即(a1+d)2=a1(a1+6d)，又因为a1=1，d≠0，所以d=4．所以Sn=na1+n(n-1)/2·d=n+2n(n-1)=2n2-n.

因此，Tn=n(2n+2)/2=n2+n.

所求取的2Tn-9bn-1+18=2(n-4)2+4≥4，只有当n=4时，等号成立.

评析本题将基本的数列问题和不等式相结合，对考查内容实施设计，属于立足于等比数列与等差数列的基础性知识，将不等式的有关思想融入其中，就能对学生对于相关知识的理解以及应用实施考查.

3.数列和解析几何综合应用

数列和解析几何的有关知识有效结合属于近些年高考数学的解答题以及压轴题当中比较常见的一种题型，根据题型的设计，通常能对学生学习相关数学思想及其应用进行深刻考查.

例如，已知在平面xOy上存在点P1(x1，y1)，P2(x2，y2)…Pn(xn，yn)，对自然数n，点Pn处于函数y=x2(x≥0)图象上，将点PN当做圆心的圆和x轴外切，Pn和Pn+1外切.已知，x1=1，xn+1

评析本题涉及到许多复杂知识点，在解答时，可将结合属性和数列性质有效结合，并通过相应转化，将问题转变为解析几何与数列问题，从而使学生实现高效求解.

综上所述，相关数列的题型相对较多，将数列知识和其他的相关知识相结合，通常是数学综合题中的重要形式，因此，在复习教学当中，需多引导学生实施归纳、类比与总结，对解题思想实施领悟，充分掌握相关解题方法，从而实现知识的巩固，并促使学生的解题能力得到有效提高.