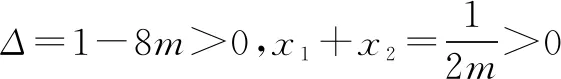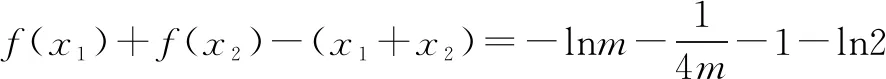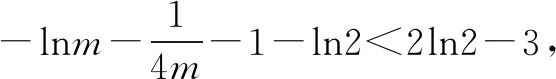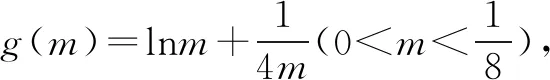借助整体思想 助力数学解题

廖秀华

(福建省上杭县第一中学 364200)

所谓整体思想是指在解题中将具有一些特征或较为复杂的部分看做一个整体，以更好的揭示相关规律，迅速找到解题突破口的一种思想.运用整体思想解答数学习题具有一定的技巧，因此教学中应注重为学生示范整体思想在解题中的具体应用，锻炼学生思维的灵活性，使其能够融会贯通，灵活应用.

一、借助整体思想解答不等式习题

不等式是高中数学的重要知识点.解答不等式的常规思路常使用基本不等式相关结论.但部分习题并不能直接应用相关结论，需要学生利用整体思想对已知条件进行转化，以达到能够直接运用基本不等式解题的目的.教学中为使学生掌握整体思想解答不等式习题的相关技巧，应做好经典例题的筛选、讲解，给学生带来良好的启发.

已知a、b、c均为正数，且满足a2+2ab+2ac+4bc=12，则a+b+c的最小值为( ).

题目灵活考查了基本不等式知识，具有一定的难度.解题的关键在于能够从已知条件入手，运用整体思想转化成可以运用基本不等式结论的形式.

二、借助整体思想解答圆锥曲线习题

计算量大是高中数学圆锥曲线习题的重要特征.但部分习题运用整体思想，可达到设而不求，降低计算难度的目的.教学中为使学生养成运用整体思想解答圆锥曲线习题的意识，应注重为学生教授相关理论，并围绕理论为学生展示整体思想在解题中的具体应用，为学生能够深入理解，学以致用奠定坚实基础.

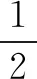
A.-1 B.-2 C.1 D.2

学生对该类题型并不陌生.解题的关键不仅要运用相关的结论，而且还应注重整体思想的应用，以减少不必要的计算，从而提高解题效率.

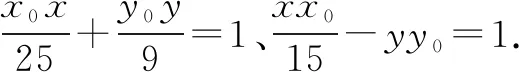
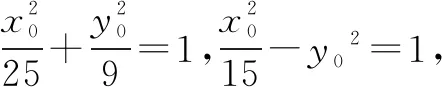
三、借助整体思想解答函数习题

函数是高中数学的重点、难点知识.习题题型复杂多变，部分习题技巧性较强，采用常规思路往往难以求解.教学中为学生认真的讲解函数相关基础知识，使学生能够自己推导、准确的记忆与函数相关的结论.同时又要围绕具体例题，鼓励学生积极思考，尝试着作答，尤其应注重给予学生点拨，引导学生利用整体思想进行分析，以帮助学生找到解题的突破口，增强其解题的自信.

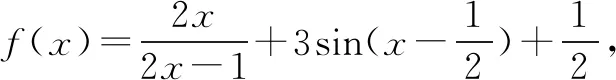
A.3025 B.3026 C.3027 D.3028

根据已知条件代入不同的自变量进行求解显然是不可取的，因此，需要认真分析f(x)表达式找到内在规律，采用整体思想进行解答.课堂上要求学生回顾所学函数对称中心知识，使学生在解题中少走弯路.

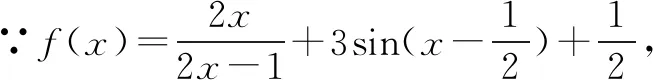
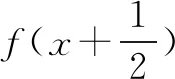
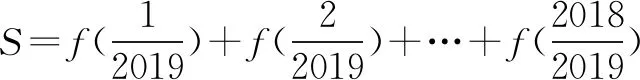
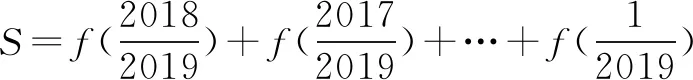
①+②得：2S=3×2018，∴S=3×1009=3027，选择C项.

四、借助整体思想解答导数习题

导数习题在一些测试以及高考中常常以压轴题的形式出现，难度较大，分值较高.为提高学生解答导数学习的能力，既要注重为学生展示整体思想在解题中的应用，使其把握整体思想应用的细节以及注意事项，又要组织学生开展针对性的训练活动，使学生在训练中深化认识，将所学知识转化为解题的能力.

已知函数f(x)=mx2+lnx，设x1，x2是f′(x)=1的两个不等的正实数解，求证：f(x1)+f(x2)+3

该题目技巧性较强，难度较大.解题的关键在于从要证明的问题入手，联系已知条件，运用整体思想、导数知识进行解答.

∵f(x)=mx2+lnx(x>0)，f′(x)=1，

∴f(x1)+f(x2)-(x1+x2)=lnx1x2+m[(x1+x2)2-2x1x2]-(x1+x2)

高中数学解题中涉及的数学思想较多，其中整体思想占有重要地位.教学中为使学生掌握整体思想相关理论以及相关的应用技巧，应做好针对性的教学设计，优选精讲例题的同时，要求学生做好听课以及日常训练的总结，不断认识与弥补应用整体思想解题的不足，促进其解题能力更好的提升.