利用“等效法”巧妙处理含理想变压器的电路问题
董静雨
(河北省石家庄市第二中学 050000)
众所周知,在中学物理中交流电部分有一大类题目含有理想变压器.由于理想变压器的存在,使得电路被分割成原线圈回路和副线圈回路两部分.有一类综合性较强的题目:含有理想变压器的电路动态分析,即当电路中的某元件变化时,牵一发而动全身,要分析回路中其它部分的电流、电压、功率的变化,因分析过程动用公式多,逻辑推理环节长,成为学生学习的难点.对于这类题目,如果能够合理的对变压器进行等效处理,那么此类题目则能够秒解.
一、变压器+负载回路:等效负载
学生已经从课本中学得:如图1所示的理想变压器的电压、功率和电流的关系分别为:

式中Ui,Pi,Ii,ni分别为原线圈(i=1)和副线圈(i=2)两端的电压、功率、电流和匝数.
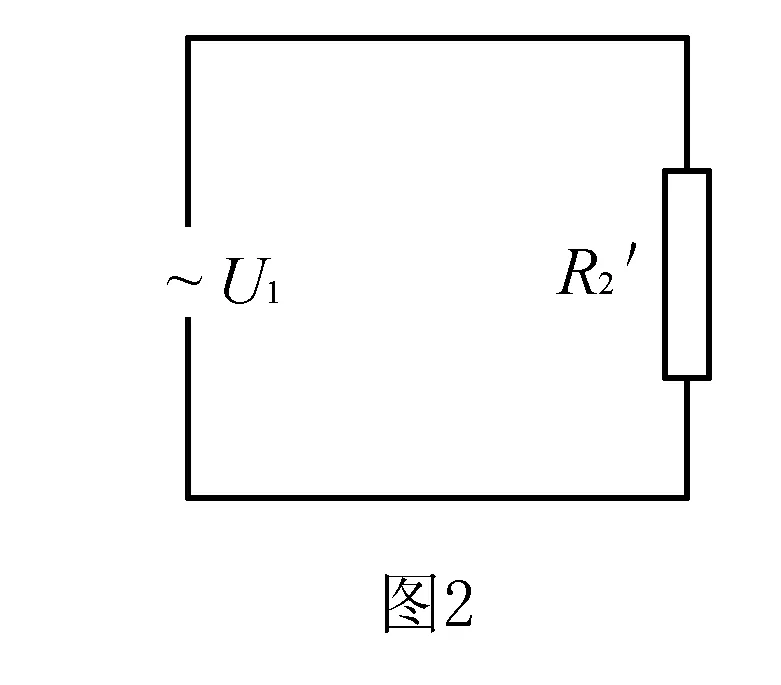


由于理想变压器原、副线圈功率相等,则有P2′=P2
上式说明等效电阻R2′与负载R2成正比,与线圈匝数比的平方成正比.这一关系可以看作是变压器的变阻关系式.
二、变压器+电源回路:等效电源
我们还可将变压器与电源看作一整体,称为等效电源.为了讨论的一般性,我们在原线圈回路中串联一电阻R1,当作电源的内阻,原电路与等效电路分别如图3和图4所示:


下面讨论等效电源的电动势E和内阻r的大小分别是多少.首先在等效电路中有闭合电路欧姆定律:
在原线圈回路中:E=U2+I2r
U1′=U1-I1R1
代入上式中得:

与等效电路中的欧姆定律比较得到等效电源得电动势和内阻分别为:
这一结果说明:变压器对电源的电动势和内阻分别单独进行了变换.
通过以上讨论我们可以更深刻的认识到:变压器在电路中同时起着变换电压、电流和负载的作用.
综上可见,利用等效观点解答含理想变压器的问题不仅能化繁为简,还可拓展解题思路,既加深了学生对知识的理解又训练了思维能力,可谓是一举多得.作为教师,培养学生学科素养的重要一环是培养学生的科学的思维,而科学思维的培养一定是依托于学生利用所学知识解决实际问题的过程.“等效法”有非常广阔的应用空间,在教学中我们有意识的去归纳整理,使学生形成思维方法,并能迁移到不同的情境中去使用,是我们最终的教学目标.

