高中物理解题中微元法的有效应用

赖鹭传

(福建省上杭县第一中学 364200)

微元法是指在处理问题时从事物的极小部分分析入手，达到解决事物整体目的的方法，在高中物理解题中有着广泛的应用.为使学生更好的理解与掌握微元法，有必要结合具体例题，为学生讲解微元法的具体应用.

一、用于解答流体问题

一枚火箭的质量为M，依靠向下方喷气在空中保持静止，若喷气的速度为v，则火箭发动机的功率为( ).

火箭发动机向下喷气时需要对气体做功，选取很小时间段内的气体为研究对象，求出火箭对气体做的功，而后运用功率计算公式便可算出火箭发动机的功率.

以很小一段时间Δt内火箭喷出的气体为对象，设喷出气体的质量为Δm，火箭发动机推气体的力为F，由动量定理得到：FΔt=Δm·v

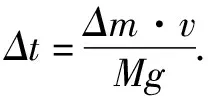
二、用于解答电场问题

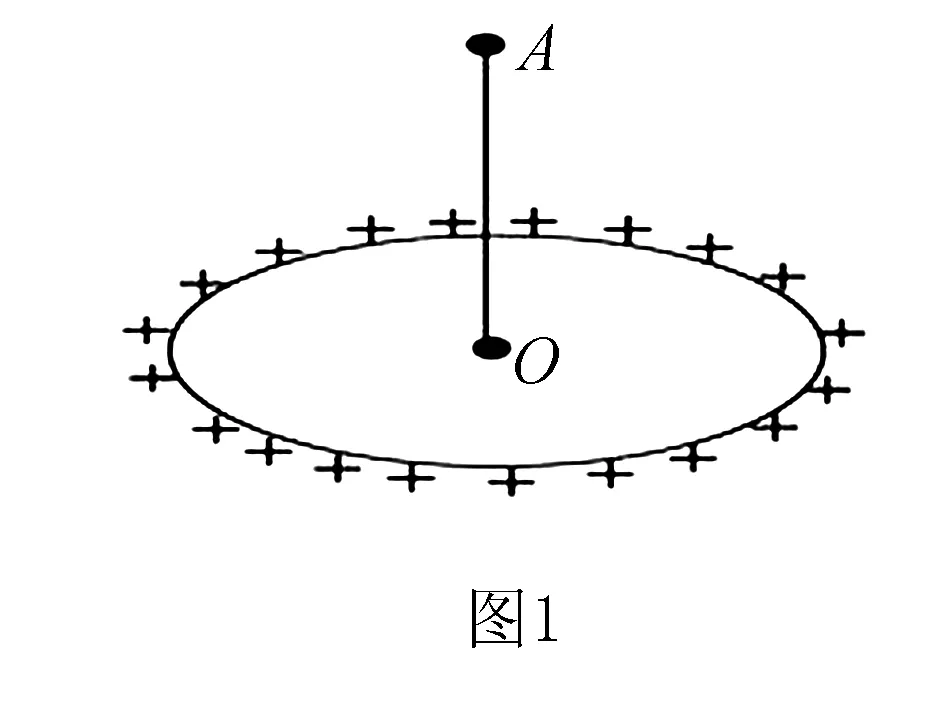
如图1，将一半径为R，均匀带电所带电荷量为+Q的圆环放置在绝缘水平面上，O为圆心.A为过圆心O竖直线上的一点，且和圆心O相距为R.将一带电量为+q的检验电荷放置在A点，则其受到的电场力的大小为____.

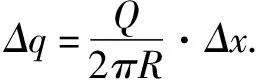
三、用于解答单棒切割问题

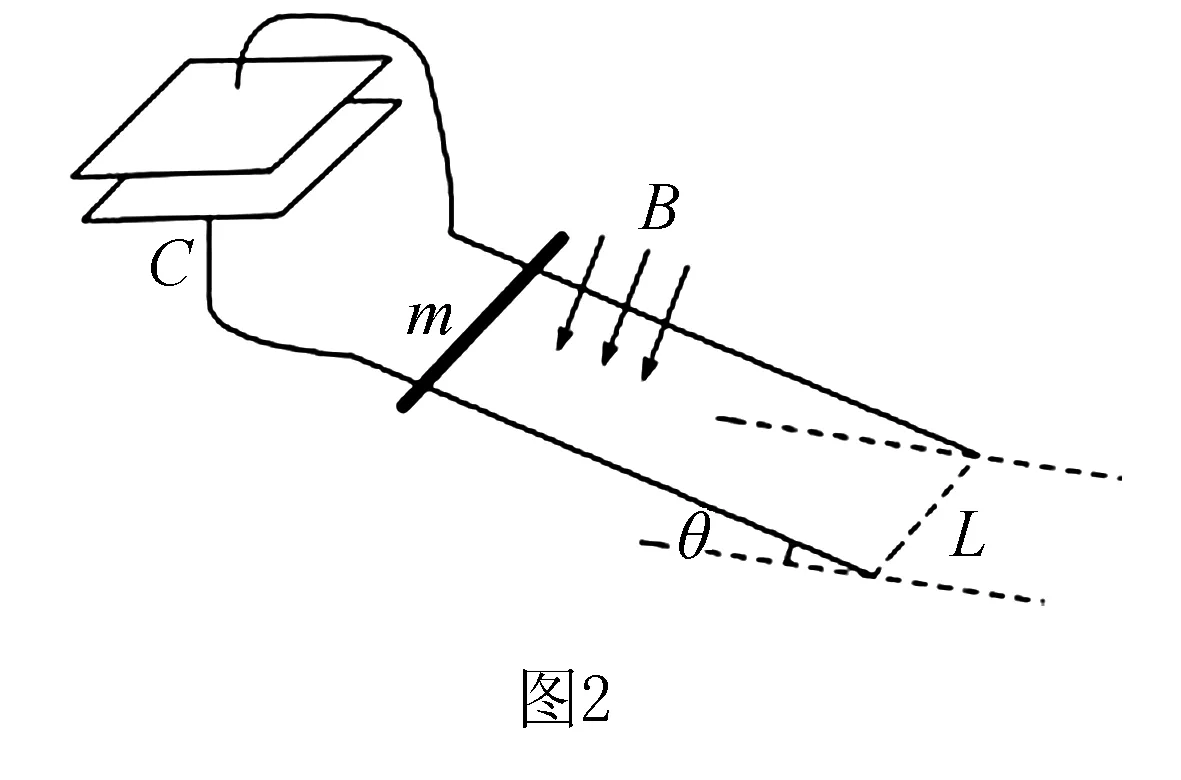
如图2，两条平行导轨间距为L，和水平面成θ角放置.两根导轨分别和一平行板电容器的两个极板相连，电容为C.导轨处在一匀强磁场中，磁场方向垂直导轨平面向下.将一质量为m的金属棒放置在导轨上，其可沿导轨下滑.下滑过程中金属棒和导轨接触良好.若金属棒和导轨间的动摩擦因数为μ，不考虑所有电阻.重力加速度为g，金属棒从导轨顶端由静止下滑.求:

(1)电容器板上的电荷量和金属棒速度大小的关系；

(2)金属棒速度大小和时间的变化关系；

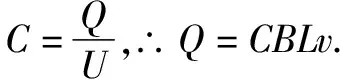
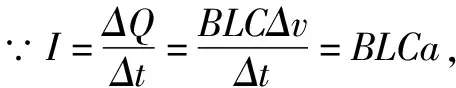
四、用于解答双棒切割问题

如图3，在竖直平面内放置两根平行的金属导轨，两导轨间的间距d=0.5m.在导轨上放着两个质量m均为0.5kg，电阻R均为0.1Ω的导体棒L1、L2和导轨构成回路，忽略其他电阻.整个空间内存在和导轨平面垂直的匀强磁场，磁场强度B=1T.两根导体棒均可在导轨上无摩擦的滑行.L1向上保持速度v匀速运动，在t=0时刻将靠近L1的L2释放.(释放时两棒的距离可忽略)经过一段时间后，L2也做匀速运动.g取10m/s2.求：

(1)若导体棒L2能向下运动，速度v的最大值.

(2)若v=3m/s，在L2刚做匀速运动的某时刻，两棒的间距为4m.在此时刻前L2运动的距离.

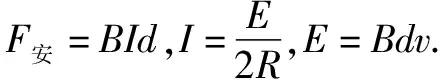
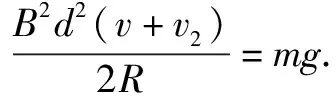
为提高学生运用微元法解答物理问题的灵活性，应结合具体教学内容为学生系统的讲解微元法相关理论，使学生真正的吃透微元法本质.同时，优选精讲典型例题，尤其注重在讲解的过程中与学生积极互动，帮助学生更好的掌握运用微元法解题的相关细节，使其遇到相关问题能够加以迅速突破.