借助模型法 解答物理难题

张 图

(四川省南充高级中学 637000)

物理涵盖很多的模型，主要有等时圆模型、渡河模型、抛体模型等.教学中既要为学生认真细致的讲解这些模型，使其掌握模型中物体的运动规律与特点，深刻理解模型内涵，又要结合具体例题讲解，为学生运用模型解题做好示范，使其真正掌握，灵活应用.

一、借助等时圆模型解题

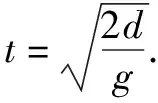
例1如图1所示，一倾角为θ的斜面上方A点放置一光滑木板AB，B端刚好在斜面上.木板与竖直方向AC所成的角为α.一物块由A端沿木板由静止下滑，要使物块滑到现斜面的时间最短，则α和θ的关系为( ).

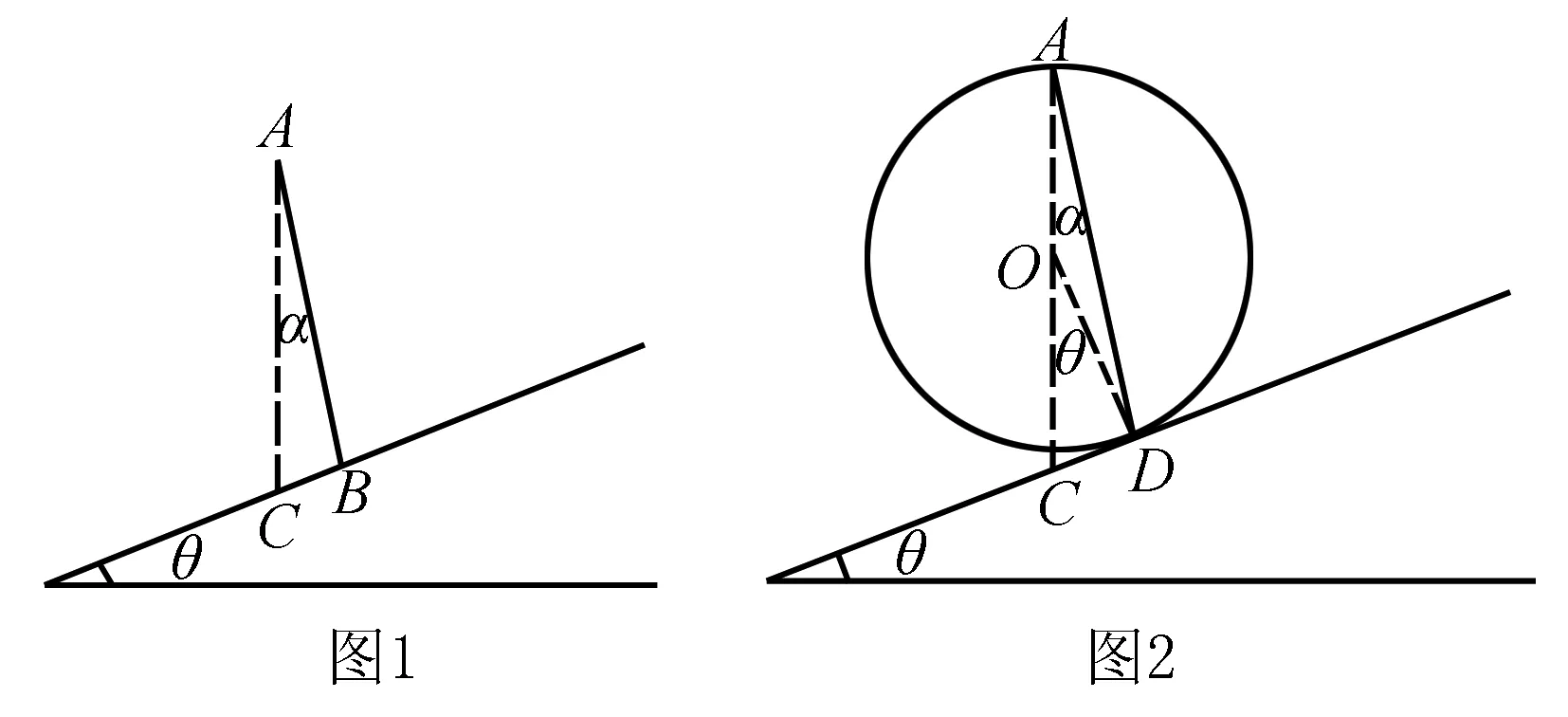
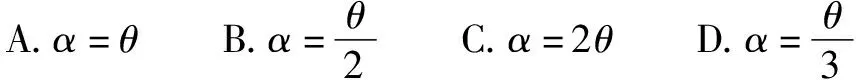
题目创设的情景较为新颖，很多学生审题后不知如何下手，究其原因在于其迁移所学知识的能力较差.该题目考查学生运用等时圆模型解题的灵活性.解答该题的关键在于结合题干中的情景构建合适位置的等时圆，课堂上可给予学生启发，使其尽快找到解题思路.

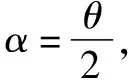
二、借助渡河模型解题

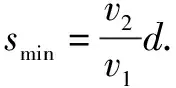
例2某人划船横渡一条河，河水流速处处相同且恒定，船的划行速度恒定.已知此人过河最短时间为T1；若此人用最短的位移过河则需时间为T2.已知船的划行速度大于水速，则船的划行速率与水流速率之比为( ).

该题目涉及船渡河时的两种情境，只有深刻理解模型，才能顺利解题.解题中应设出合理参数，借助模型直接求出渡河最短时间的表达式.在探讨船的最短位移时引导学生绘制相关的草图，联系所学模型，找到速度之间的关系.

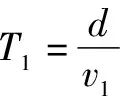
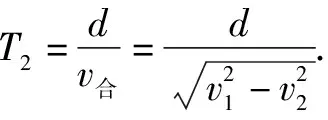
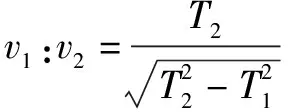
正确选项为A.

三、借助抛体模型解题

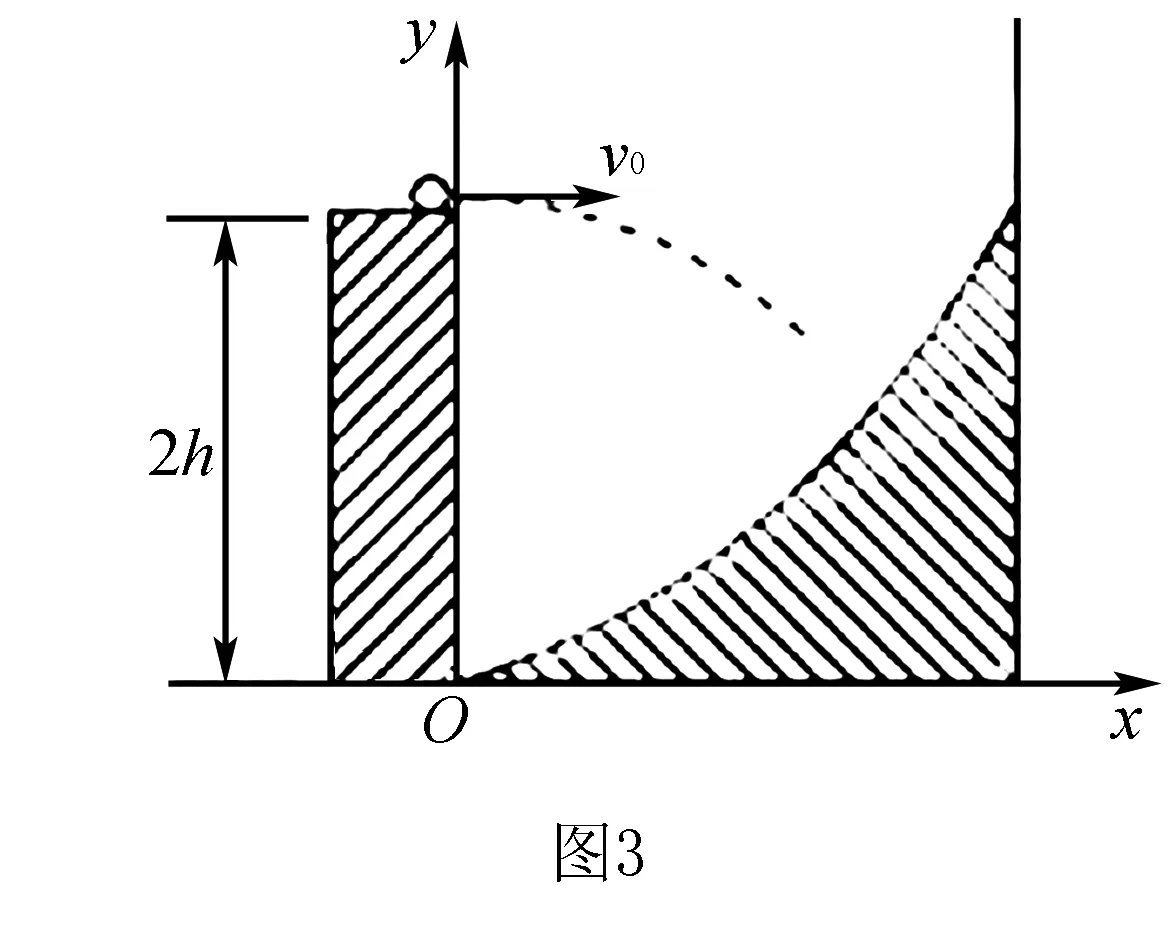
该题目创设的情境并不复杂，但却涵盖很多知识，主要有抛体模型、动能定理以及数学知识等.教学中要求学生认真审题，积极回顾所学的抛体模型，建立相关的方程，表示出Ek，而后运用数学知识求其最小值.

设探险队员跳到平面上时的水平位移为x，竖直位移为H.

由几何关系可得y=2h-H，

由数学知识得到

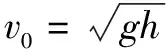
高中物理教学中注重相关模型的讲解对提高学生的解题能力具有重要的促进作用，因此，应结合教学进度灵活采用多种方法，做好物理模型教学工作，尤其应创设具有难度的试题，训练学生运用模型解题的技能，促进其解题水平与能力的进一步提升.