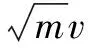图像法在碰撞问题中的应用——以2020年山东省高考物理题为例

周 彬 倪亚贤

(1.江苏省苏州大学物理科学与技术学院 215006;2.江苏省苏州大学东吴学院 215006)

一、原题呈现及命题意图分析

如图1所示，一倾角为θ的固定斜面的底端安装一弹性挡板，P、Q两物块的质量分别为m和4m，Q静止于斜面上A处.某时刻，P以沿斜面向上的速度v0与Q发生弹性碰撞.Q与斜面间的动摩擦因数等于tanθ,设最大静摩擦力等于滑动摩擦力.P与斜面间无摩擦，与挡板之间的碰撞无动能损失.两物块均可以看作质点，斜面足够长，Q的速度减为零之前P不会与之发生碰撞.重力加速度大小为g.

(1)求P与Q第一次碰撞后瞬间各自的速度大小vP1、vQ1；

(2)求第n次碰撞使物块Q上升的高度hn；

(3)求物块Q从A点上升的总高度H；

(4)为保证在Q的速度减为零之前P不会与之发生碰撞，求A点与挡板之间的最小距离s.

2020年高考物理大纲要求在考查知识的同时注重考查能力，从而促使学生从解题向解决问题转变.本题是一道多过程的碰撞问题，考查的知识点有动量守恒定律、能量守恒定律、匀变速运动规律和动能定理等，突出考查了学生的分析综合能力和运用函数图像分析问题的能力.基于上述考查目标，要求学生具备运动与相互作用观念，依次分析各物块的运动情况以及物块间的相互作用情况，将多过程问题分解为若干单过程问题.要求学生具备能量观念，明确弹性碰撞前后瞬间能量守恒的特点，而非碰撞全过程能量守恒.要求学生具备模型建构、科学推理和科学论证的科学思维，建构弹性碰撞模型和匀变速运动模型，运用数学知识进行推理论证，得到相邻两次碰撞间系统动量和动能的关系，明确碰撞无穷多次的特点.本题不同于光滑水平面上的碰撞问题，碰撞全过程中系统总能量逐渐减小，借助图像则可以很好地表达这个特征.

二、题目解析

(4)本小问考查匀变速运动规律，与图像无关，限于篇幅略去解析.

三、图像应用

为了进一步说明图像法在碰撞问题中的应用，下面以三道题为例，重点说明如何通过图像的截距、斜率和半径对问题进行定性分析，从而避免复杂的计算.

1.直线截距的应用

例1在光滑水平面上有两个物块1和2相向运动，物块1运动方向向右，取水平向右为正方向，两物块总动量大于0，物块1和2发生弹性碰撞后，物块2的速度大小如何？速度方向如何？

解析参考引言部分建立方程组，已知v1>0，v2<0，P>0，需要判断v2′的大小和方向，利用解析法较难判断.

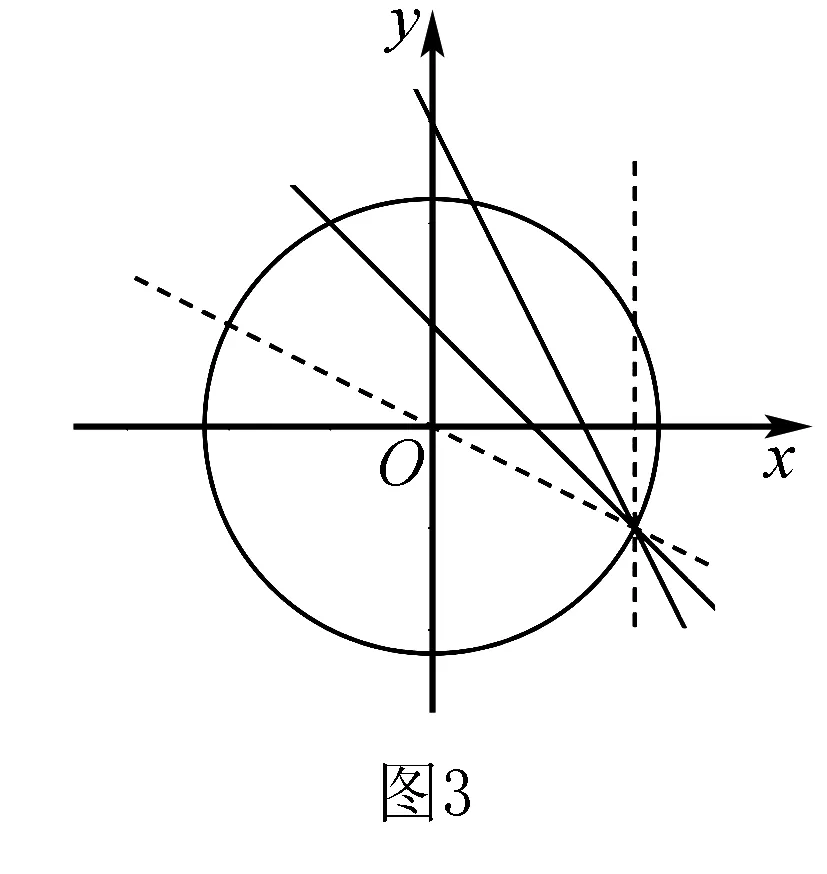
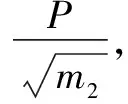
2.直线斜率的应用

解析同上建立方程组，其中m1、m2、v1′、v2′均为未知量，较难进行判断.

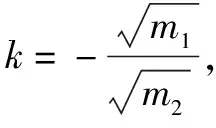
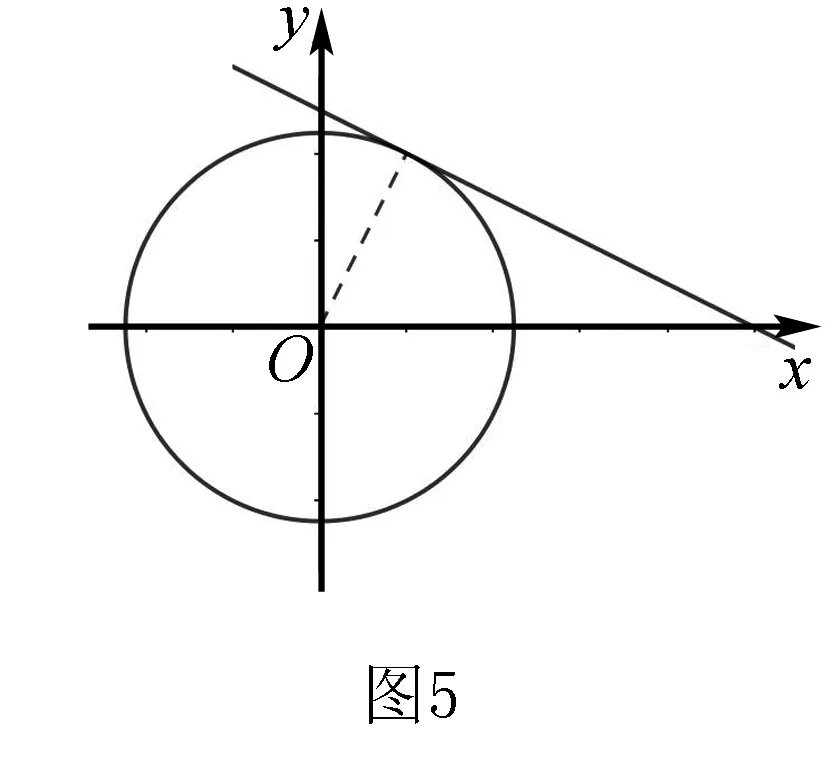
3.圆的半径的应用

例3在光滑水平面上有两个物块在一条直线上运动，物块质量分别为m1、m2，总动量为P，要使两物块发生碰撞，物块总动能至少为多少？

解析法同上建立方程组，其中v1、v2线性相关，需要判断在v1′、v2′有解的情况下，Ek的最小值，较难判断.