珊瑚岛礁孤立波爬坡的平面二维数值模拟研究
刘林平,刘维杰, 2,孙志林
(1. 浙江大学 海洋学院,浙江 舟山 316021;2. 南京水利科学研究院 水文水资源与水利工程科学国家重点实验室,江苏 南京 210029)
海啸波通常由海底地震、火山爆发或者山体滑坡等引起,并通过沿岸爬坡过程侵袭陆地,造成极大的破坏,因此研究海啸波在近岸地区的传播以及爬坡过程具有重要的科学和工程意义。尽管实际海啸波通常以瞬态非周期性的形式出现,但孤立波被认为可模拟海啸首波的一些重要特征,因此学者通常采用孤立波进行海啸波的物模试验以及数值模拟研究[1-5]。自印度洋海啸之后,珊瑚礁在抵御海啸袭击中的作用引起了人们的重视,但众多灾后调查发现珊瑚礁对于海啸灾害的防御程度不一[6]。因此,为了更好地了解珊瑚礁在抵御海啸侵袭过程中的作用,学者们进行了相应的物理模型试验和数值模拟来探究珊瑚礁不同地形和水动力参数对海啸灾害的影响。
在物理模型试验方面,Quiroga等[7]通过大比尺水槽试验研究了礁床粗糙度对孤立波在礁坪上传播的影响;Yao等[8]在水槽试验中采用圆柱体阵列近似模拟了珊瑚礁大糙率表面,并提出了预测珊瑚礁海岸孤立波爬高的经验公式。相比物理模型试验,数值模拟能更便捷地调整珊瑚礁地形参数(如礁坪宽度、礁前斜坡、礁后斜坡等)和水动力参数(如礁坪水深、入射波高、珊瑚礁糙率等)。过去的几十年中,Boussinesq方程因其计算精度和效率较高的优势,在珊瑚礁波浪水动力数值模拟研究中应用最为广泛[9-14]。对于珊瑚礁孤立波传播和爬坡,Zhou等[15]利用Boussinesq波浪模型研究了珊瑚礁地形和水动力参数对孤立波在礁缘附近的反射、破碎和透射的影响。Yao等[8]和Ning等[11]利用Boussinesq波浪模型研究了地形和水动力参数对礁后孤立波爬坡高度的影响。Liu等[16]利用Boussinesq波浪模型进一步发现,礁前斜坡的坡度对孤立波爬坡带内最大动量通量的影响与对爬高高度的影响有所不同。这些研究有助于理解不同因素对缓解珊瑚礁海岸海啸灾害的重要性,也展现了Boussinesq模型模拟珊瑚礁陡变地形上孤立波传播和爬坡的能力。
然而,目前有关珊瑚礁对海啸灾害影响的研究仍只局限于水平一维(二维地形)的研究,即假设地形在沿岸方向无变化,波浪在沿岸方向无流速,实际更适用于沿大陆分布的岸礁地形上的波浪运动。但对于诸如南海岛礁的孤立岛屿,波浪的绕射和折射现象不容忽视,水平一维研究无法充分展示在此情况下珊瑚礁各地形、水动力因素对礁后孤立波最大爬高分布的影响。因此为了弥补现有研究的不足,采用激波捕捉类Boussinesq模型FUNWAVE-TVD[17],对三维岛礁地形上的孤立波传播和爬坡开展平面二维数值模拟,利用已有物理模型试验数据验证了模型模拟孤立波在三维岛礁地形上传播与爬坡的能力,并进行了一系列的数值试验探究了珊瑚礁对岛屿周围孤立波最大爬高分布的影响。
1 模型介绍
采用的数值模型是Shi等[17]提出的FUNWAVE-TVD, 控制方程基于Chen等[18]提出的完全非线性Boussinesq方程,并结合Kennedy等[19]提出的参考水深法,其连续性和动量控制方程:
(1)
(2)

(3)
其中,H=h+η表示当地总水深,h为静水深。
(4)
(5)
(6)
(7)
式中:V1和V2表示Boussinesq方程的色散项,V3表示的是色散项O(μ2)对w×u=wiz×u的贡献,其中iz表示z方向的单位向量,w表示垂向速度。R表示底部摩擦和网格侧向湍流引起的扩散和耗散项,其中底摩擦项为结合曼宁系数的二次摩擦项:
(8)
其中,n表示曼宁系数。
在FUNWAVE-TVD中,上述控制方程被进一步调整为守恒形式且空间上的离散采用有限体积和有限差分的混合数值格式。时间步长采用非线性空间离散化的三阶强稳定性(SSP)Runge-Kutta方法,并根据Courant-Friedrichs-Lewy(CFL)标准选择自适应时间步长。基于混合数值格式,波浪破碎处理采用激波捕捉法,即当波面升高同当地水深的比值达到某一临界值时,将Boussinesq方程退化为带有TVD格式的非线性浅水方程进行波浪破碎计算,忽略Boussinesq方程中的高阶非线性项和色散项,根据Tonelli等[20]的研究,模型中判断波浪破碎的临界值为0.8。干湿界面处通过修正黎曼解的特征速度实现海岸动边界波浪爬坡的计算。有关模型的具体内容可进一步参考文献[17]。
2 模型验证
对于孤立波在二维珊瑚礁陡变地形上传播和爬坡的模拟,本模型已得到了充分的验证[5,11],因此这里仅利用Briggs等[2]的港池试验数据来验证模型在模拟三维岛屿地形上孤立波传播和爬坡的可靠性。基于Briggs等的试验,数值港池设置的平面和剖面布置如图1所示。数值港池长为35 m,宽30 m,港池中设置有坡度为1∶4的圆台来近似实际岛屿,圆台的中心在x=23 m,y=15 m的位置处,造波带设置在x=9 m的位置,港池水深为0.32 m,港池两侧设置有海绵层来吸收反射波。物理模型试验中共设置了27个浪高仪来测量波面高程的变化,选取了其中四个浪高仪的数据用于模型验证,分别为迎浪面的6号和9号浪高仪,岛屿背浪面的22号浪高仪和岛屿侧面的16号浪高仪,其具体位置如图1所示。同时,试验也在圆台周围布置了爬高计来测量岛屿周围的孤立波最大爬坡高度。

图1 基于Briggs试验的数值模型设置Fig. 1 Numerical setup based on Briggs’ experiments
数值模拟中,网格设置为0.05 m×0.05 m, 曼宁系数设置为0.012以表征岛屿物理模型表面光滑混凝土的糙率,输出数据的时间步长为0.02 s。图2展示了入射孤立波波高为0.014 m时四个浪高仪位置处本文模型预测的波面随时间变化与试验数据的对比,同时也展示了Lynett等[21]与Fuhrman等[22]所用Boussinesq模型的计算结果。如图2所示,三种模型计算结果相近且均与试验数据的吻合程度较好,但在浪高仪9的位置,本文模型对于波峰略有高估,这可能是由于本文模型采用激波捕捉处理波浪破碎造成的。图3展示了模型预测岛屿周围的相对最大爬高(最大爬坡高度与入射波高的比值)与试验数据的对比,同时也展示了Lynett等[21]与Fuhrman等[22]所用Boussinesq模型的计算结果。图中选取了圆台一侧十个测点,横坐标表示测点与圆台圆心的连线与入射波方向的夹角α的度数。如图3所示,相比Lynett等[21]与Fuhrman等[22]的计算结果,本文模型总体上更为准确地模拟了岛屿周围的最大爬高分布特征,表明本文模型的混合数值格式在预测波浪爬坡的可靠性和优越性。图3中岛屿迎浪面和背浪面都出现比较大的爬高,且背浪面出现的爬高比迎浪面的更大,这一现象主要是波浪经过岛屿地形时发生绕射与折射,流向发生改变,波能会在背浪面汇集,使得背浪面爬高急剧增加[3]。

图2 模型计算的波面高程随时间变化与试验结果对比Fig. 2 Comparison of computed and measured time series of surface elevations

图3 模型预测岛屿周围相对最大爬高与试验结果对比Fig. 3 Comparison of computed and measured maximum runup heights around the island
3 数值试验设置
在验证了模型预测岛屿周围孤立波传播和爬坡的能力后,设置了一系列现场尺度的数值港池试验用于探究珊瑚礁地形和水动力因素对岛礁周围孤立波最大爬高的影响。数值港池试验设置如图4所示,港池长17 km,宽16 km,网格大小为10 m×10 m。港池中设置有概化的圆形珊瑚岛礁,岛礁原型为印度尼西亚(南纬8°25′32″,东经122°30′30″)的Babi岛(如图5所示),该岛四周发育有成熟珊瑚礁。利用Google earth得到Babi岛的海岸线周长约为6 400 m,珊瑚礁礁缘的周长约为9 000 m,将其概化为圆形得到海岸线直径D约为2 044 m,礁坪宽约为400 m。岛礁的中心位于x=8 km,y=8 km的位置,内部造波带位于x=3 km。在上述岛礁参数的基础上,共设置了4组数值试验,分别研究水动力(入射波高H、礁坪水深hr、珊瑚礁糙率n2)及珊瑚礁地形(礁坪宽度w、礁前斜坡坡度Cotθ、礁后斜坡坡度Cotβ)参数对岛礁周围孤立波爬坡的影响。各组数值试验工况如表1所示,每组工况参数的取值变化范围均根据现有文献报道设定,其中礁坪宽度的变化范围(50~1 000 m)、礁坪水深的取值(3 m)和变化范围(1~5 m)、礁前(后)斜坡坡度取值(4)和变化范围(1~20)根据Quataert等[23]总结的珊瑚礁参数设定,珊瑚礁糙率的取值(0.09)和变化范围(0.02~0.09)根据Gelfenbaum等[6]的研究确定,入射波高取值(2 m)根据Ford等[24]的文献报道确定,入射波高变化范围(1~6 m)以及礁前水深hd的取值(60.5 m)根据Briggs等[2]物理模型试验中采用的入射孤立波的非线性系数范围(入射波高与水深的比值)而确定。此外,港池底床的曼宁系数设置为n1=0.02(沙质底床),礁后斜坡的曼宁系数设置为n3=0.04(砾石),数值模拟中数据输出的时间步长为1 s。
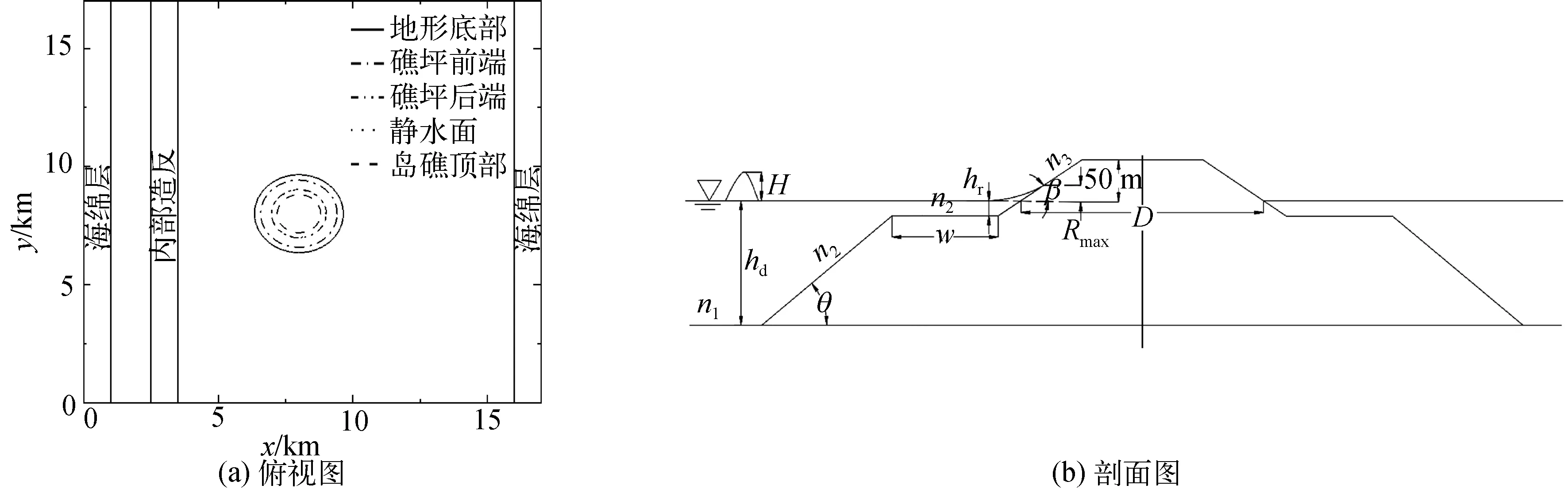
图4 数值试验设置Fig. 4 Numerical experiment setup

图5 巴比岛 (Google Earth)Fig. 5 Babi island (Google Earth)

表1 数值试验工况
4 结果与讨论
图6展示了组1珊瑚岛礁四周孤立波最大爬高随入射波高的变化。如图6所示,珊瑚岛礁四周的最大爬高随着入射波高H的增大而不断增大,入射波高为6 m的迎浪面(α=0°)最大爬高相比入射波高为1 m的计算结果增大约250%,背浪面(α=180°)最大爬高增大约125%。图中结果也显示入射波高越大爬高增大的幅度越小,这主要是因为波高越大波浪的破碎程度越强烈,能量损耗更大,一定程度上减弱了爬坡高度的增长,该结果也与前人水平一维研究[3,11]的成果类似。
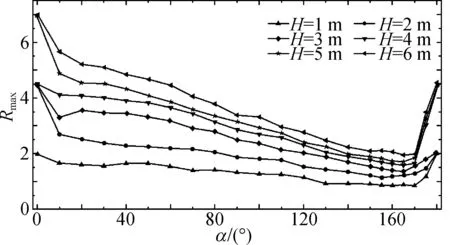
图6 岛礁四周孤立波最大爬高随入射波高的变化Fig. 6 Variation of maximum runup height around the reef-fringed island with different incident wave heights
图7展示了组2珊瑚岛礁四周孤立波相对最大爬高随礁坪水深的变化,同时也展示了无珊瑚礁(仅圆台岛屿)时,岛屿四周的相对最大爬高分布情况。如图7所示,珊瑚岛礁周围的相对最大爬坡高度均随礁坪深水的增大而不断增大,当礁坪水深为1 m时,相比于无珊瑚礁岛屿,迎浪面(α=0°)最大爬高可降低70%,背浪面(α=180°)最大爬高可降低56%,而礁坪水深增大至5 m时,相比于无珊瑚礁岛屿,迎浪面(α=0°)最大爬高仍可降低约36%,但背浪面波能汇集区域的最大爬高已经与无珊瑚礁时相差无几,表明礁坪水深增大到一定程度时,岛礁背浪面的孤立波爬坡高度将不受岛屿周围珊瑚礁的影响。

图7 岛礁四周孤立波相对最大爬高随礁坪水深的变化Fig. 7 Variation of relative maximum runup height around the reef-fringed island with different reef flat water depths
图8展示了组3中珊瑚岛礁四周孤立波相对最大爬高随礁坪宽度的变化。如图8所示,珊瑚岛礁周围的相对最大爬坡高度均随礁坪宽度的增大而不断减小。当礁坪宽度为800 m时,相比于无珊瑚礁地形,迎浪面(α=0°)最大爬高降低约71%,背浪面 (α=180°) 最大爬高降低约56%。当礁坪宽度为100 m,整个珊瑚岛礁四周的相对最大爬高已与无珊瑚礁时十分接近,甚至当礁坪宽度只有50 m时,珊瑚岛礁的相对最大爬高会高于无珊瑚礁时的爬高,该结果也与部分学者[6]的观点一致,珊瑚礁的存在未必总是能降低波浪灾害,其陡变地形引起的波浪强非线性作用有时可能会加剧波浪灾害,尤其是珊瑚礁本身的能量损耗作用较弱的时候。

图8 岛礁四周孤立波最大爬高随礁坪宽度的变化Fig. 8 Variation of relative maximum runup height around the reef-fringed island with different reef flat widths
图9展示了组4珊瑚岛礁四周孤立波相对最大爬高随礁前斜坡坡度的变化。如图9所示,礁前斜坡坡度对岛礁周围的爬高分布影响几乎没有影响,该结果也与前人水平一维研究[5,11]的成果类似。尽管礁前斜坡变缓会降低波浪反射,但礁前斜坡变缓也会使波浪破碎点向外海方向移动,使得波浪破碎提早发生,能量损耗更多。
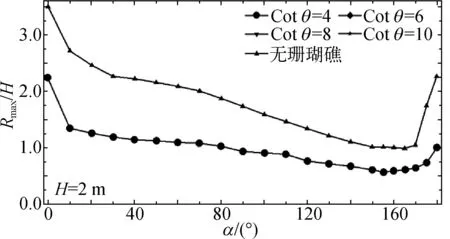
图9 岛礁四周孤立波最大爬高随礁前斜坡坡度的变化Fig. 9 Variation of relative maximum runup height around the reef-fringed island with different fore-reef slopes
图10展示了组5珊瑚岛礁四周孤立波相对最大爬高随珊瑚礁糙率的变化。如图10所示,珊瑚岛礁周围的相对最大爬坡高度均随珊瑚礁糙率的减小而不断增大,整个珊瑚岛礁周围,相比于无珊瑚礁地形,珊瑚礁糙率为n2=0.09时迎浪面(α=0°)最大爬高降低约36%,背浪面(α=180°)最大爬高降低约56%。当珊瑚礁糙率减小至n2=0.03时,除迎浪面部分区域(α<30°)外,岛礁周围的相对最大爬高已经与无珊瑚礁时相差无几,这与礁坪宽度的影响相似。而当珊瑚礁糙率减小至n2=0.02时,岛礁周围的相对最大爬高甚至会高于无珊瑚礁时的爬高,该现象的原因应与图8中礁坪宽度为50 m的情况类似,当珊瑚礁本身的能量损耗作用较弱的时候,其陡变地形引起的波浪强非线性作用反而会加剧波浪灾害。值得一提的是,n2=0.02通常用于近似表征珊瑚礁因白化而彻底死亡以后的表面糙率[6],由此可见,气候变化引起的珊瑚礁白化不仅会降低珊瑚礁对海啸灾害的防御作用,甚至会加重致灾程度。

图10 岛礁四周孤立波最大爬高随珊瑚礁糙率的变化Fig. 10 Variation of relative maximum runup height around the reef-fringed island with different reef roughnesses
图11展示了组6珊瑚岛礁四周孤立波相对最大爬高随礁后斜坡坡度的变化。如图11所示,珊瑚岛礁周围的相对最大爬坡高度随礁后斜坡坡度的变缓而有所减小,礁后斜坡坡度为20的迎浪面(α=0°)最大爬高相比礁后斜坡坡度为2的计算结果降幅约38%,背浪面(α=180°)最大爬高降幅约33%,这主要是由于随着礁后斜坡的变缓,波浪在水平方向上传播的距离变大,波浪在整个爬坡过程中会有更多的摩擦损耗。

图11 岛礁四周孤立波最大爬高随礁后斜坡坡度的变化Fig. 11 Variation of relative maximum runup height around the reef-fringed island with different back-reef slopes
5 结 语
基于验证后的激波捕捉类Boussinesq模型FUNWAVE-TVD对孤立波在三维珊瑚礁岛屿附近的传播和爬坡进行了现场尺度的水平二维数值模拟,分别研究了入射波高、礁坪水深、礁前斜坡、礁坪宽度、珊瑚礁糙率、礁后斜坡对岛礁周围孤立波最大爬坡高度的影响。结果表明:总体上珊瑚礁的存在可有效降低岛屿四周孤立波的最大爬坡高度,入射波高、礁坪水深、礁坪宽度、珊瑚礁糙率是影响珊瑚岛礁四周孤立波爬坡分布的主要因素,岛礁四周最大爬坡高度会随入射波高和礁坪水深的增大、礁坪宽度和珊瑚礁糙率的减小而不断增大。当礁坪水深增大到一定程度时,岛礁背浪面的孤立波爬坡高度将不受岛屿周围珊瑚礁的影响,而当礁坪宽度和珊瑚礁糙率减小至一定程度时,会出现岛礁四周最大爬高高于无珊瑚礁时爬高的现象。礁后斜坡的变缓会使岛礁周围的最大爬高有所减小,而礁前斜坡坡度对珊瑚岛礁周围的最大爬高几乎没有影响。

