新型激光雷达浮标运动响应特性数值研究

郭晨伟，高洋洋, ，国 振，王立忠,

(1. 浙江大学 海洋学院，浙江 舟山 316021; 2. 浙江大学 海南研究院，海南 三亚 572024; 3. 海洋感知技术与装备教育部工程研究中心，浙江 舟山 316021)

随着对海洋油气矿产等资源开发力度的增大，亟需采用海洋浮标获取相关海域的风、浪、流等气象水文实测资料[1]。目前典型的海上浮标类型主要包括铁饼形、类Spar式圆盘形及多体组合式碗形等结构型式。与固定式监测结构相比，海洋浮式浮标观测系统采用先进的海洋环境资料观测技术，具有使用寿命长，可长期、定点、连续测量，并且自动实时同步数据等优点，在使用的灵活性、成本以及功能性上具有更大的发展空间[2]。

海洋浮标在台风等极端海洋环境下经常会发生走锚事故[3]，对邻近海域的其他浮标、船舶、海洋平台等海洋工程造成一定的安全隐患。而浮标标体结构运动响应及锚泊系统设计直接关系到浮标稳定性和可靠性，是影响浮标在布放海域定点长期工作的重要因素。Jenkins等[4]和Carpenter等[5]对比分析了圆柱形和圆盘形浮标水动力性能，发现圆柱形浮标垂荡性能优于圆盘形浮标。Pual等[6-7]研究发现在张紧式和悬链线式系泊方式下浮标的力学性能和运动响应存在较大差异，在特定海况条件下悬链线系泊方式产生的动态张力可达到张紧式的3倍。Kim等[8]研究圆柱形浮标在周期性波浪作用下的运动响应和锚链张力，发现在恶劣的海况下潜水浮标的运动响应优于漂浮式浮标。Zhu等[9]研究发现当球形浮标采用两点对称系泊方式时，浮标纵向运动位移与纵向和横向入射波相关，而横向运动位移仅与横向入射波相关。Gomes等[10]研究发现在柱形浮标体上加装不同形状的连接板可以有效减少浮标侧倾和俯仰运动，安装在浮标底部的连接板可以最大程度地增加浮标侧倾和俯仰运动的阻尼。Huang等[11]研究发现柱形波浪浮标在各自由度均进行近似周期性的正弦运动，不同运动自由度之间的耦合效应会导致某一个自由度的振幅增加而其他自由度上的振幅减小。近年来，结合传统海洋资料浮标与新型激光雷达测速装置的优点，提出了一种新型激光雷达测速海洋浮标装置[12]。新型激光雷达浮标作为海上风能评估的重要应用，与传统型固定式风能测量装置相比，具有非接触、精度高、技术维护容易、成本低等诸多优势[12-13]。近年来关于新型激光雷达浮标海上试验结果验证了其与传统海上测风技术相比，测风精度更为准确[14-18]。然而激光雷达浮标工作时对其系统稳定性、储能供电能力、运动响应控制等均要求非常严格[19]。为了减少极端海洋环境条件下浮标的走锚、断锚事故，新型激光雷达浮标锚泊系统的结构形式以及系留方式成为浮标设计中的关键[20-21]。新型激光雷达浮标的研究起步较晚，欧美国家目前已在积极开展新型激光雷达浮标设计优化与实海测试。与欧美国家相比，我国关于新型激光雷达浮标技术的研究还处于起步阶段，开展激光雷达浮标运动响应和锚泊张力特性研究，可为激光雷达浮标优化设计及安全防护提供技术支撑，具有重要的科学意义和工程应用价值[19]。

综上所述，针对一种新型的激光雷达浮标结构型式，基于ANSYS/AQWA软件建立风浪流荷载作用下雷达浮标水动力计算模型，研究了浮标吃水深度、形状参数对于激光雷达浮标运动响应以及风浪流入射角度对其系泊张力特性的影响规律。计算结果验证了新型激光雷达浮标系统的适用性，为激光雷达浮标的设计优化提供技术参考。

1 数学模型

1.1 控制方程

假定海水为无黏性、不可压缩以及均匀的理想流体[22]，基于势流理论开展激光雷达浮标与波浪相互作用研究。将浮标周围的波动场内任意一点的速度势记为Φ(x,y,z,t)，关于速度势的求解可分为以下三个部分：

Φ(x,y,z,t)=ΦI(x,y,z,t)+ΦD(x,y,z,t)+ΦR(x,y,z,t)

(1)

其中，ΦI(x,y,z,t)为扰动的入射波速度势，ΦD(x,y,z,t)为绕射速度势，ΦR(x,y,z,t)为辐射速度势，其中绕射速度势和辐射速度势合称为散射速度势ΦS。入射速度势ΦI和散射速度势ΦS求解均需满足一定的定解条件，即拉普拉斯方程，自由表面边界条件，海底边界和结构物表面边界条件[22]。此外，散射速度势ΦS求解尚需满足结构物无穷远边界条件，即Sommerfeld条件[23]。对于散射速度势的求解一般采用格林函数法，即：

(2)

其中，G(x,y,z;ξ,η,ζ)为格林函数，满足拉普拉斯方程、自由表面边界条件、海底边界和结构物表面边界条件以及结构物无穷远边界条件。将求解得到散射速度势与入射速度势叠加，得到浮标周围波浪场内任意一点的总速度势Φ(x,y,z,t)，基于Bernoulli方程进一步求得浮标表面上的水动力压力：

(3)

其中，ρ为海水密度,p(x,y,z,t)为浮标表面上的水动力压力。

作用在浮标结构上的波浪力可由水动力压力沿浮标结构表面积分得到，即：

(4)

其中，F为作用在浮标结构表面的波浪力，n为浮标外表面单位法向向量，S为浮标的瞬时湿表面。

频域内规则波作用下的浮标运动平衡方程：

(5)

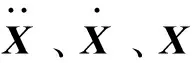
时域内系泊浮标系统运动响应方程：

(6)

其中，K(t-τ)为系统延迟函数矩阵；Fi(t)为作用在浮标结构上的环境作用力；Fm(t)为系泊作用力。

1.2 数学模型

海洋激光雷达浮标作为一种新型的浮标结构形式，其上部布置包括风速风向测速仪、天线、避雷针、太阳能电池板以及若干数据采集系统。浮标主体采用上部圆台形浮筒、中部圆柱形浮筒、下部对称圆台形浮筒及下部立柱和垂荡配置块的结构形式。浮标内部为多舱结构，布置数据采集系统以及蓄电池等装置。激光雷达浮标结构的主尺度以及主要参数如表1所示，整体模型示意与网格示意如图1所示。

表1 浮标主尺度以及主要参数

图1 选型浮标模型与网格示意Fig. 1 FLiDAR buoy model configuration and mesh setting

激光雷达浮标系统作业水深150 m，通过两点锚泊方式固定，两根锚链沿x轴方向呈对称分布形式，锚固点之间间距为300 m。海底处锚体基础采用水泥重块固定，系泊缆参数如表2所示。系泊缆全部采用整段锚链，一端与海底处锚体相连，一端与激光雷达浮标上部的导缆孔处相连接，如图2所示。

表2 系泊缆参数

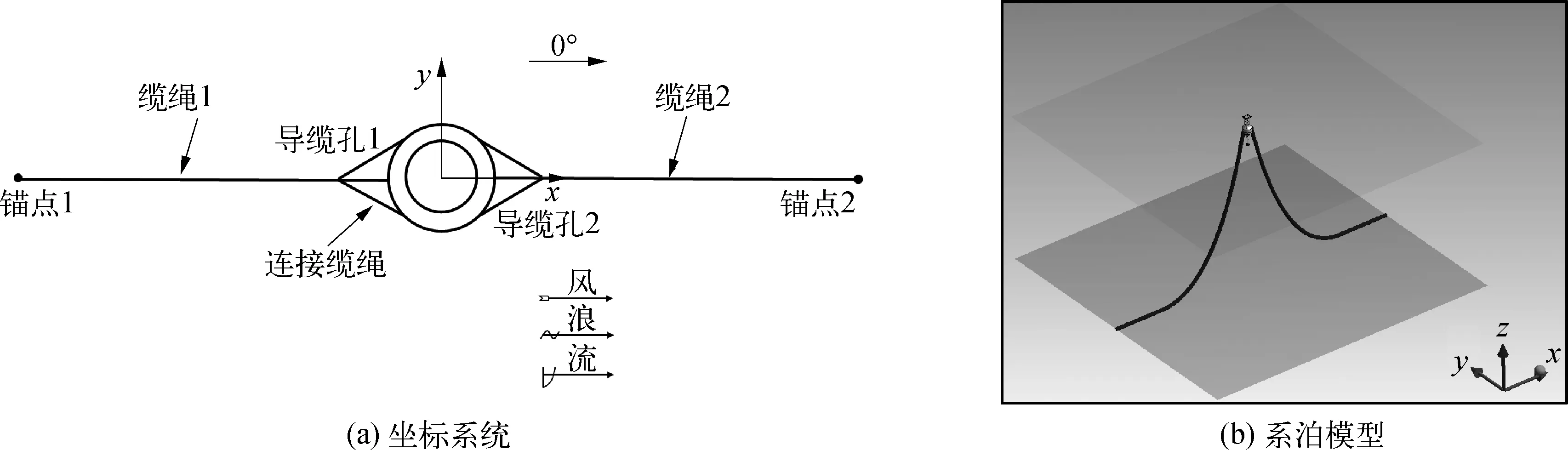
图2 浮标锚泊系统示意Fig. 2 FLiDAR buoy mooring system

以下将考虑浮标的吃水深度、下部浮筒形状并进行频域计算，分析激光雷达浮标在自由振荡时的频域响应特点。由于激光雷达浮标结构设计的对称性，本研究主要以浮标在x和z方向上的运动响应作为研究对象，同时考虑附加质量、辐射阻尼、幅值响应算子(RAO)以及一阶波浪力与二阶波浪力等参数影响变化。

2 激光雷达浮标水动力性能

2.1 吃水深度对浮标水动力性能的影响

浮标装置内部设置为多个单独舱室，其吃水深度变化会直接影响其搭载性能。通过改变浮标质量、吃水深度及重心位置参数，研究了激光雷达浮标水动力性能的变化，具体参数如表3所示。图3为不同吃水深度下浮标纵荡和垂荡运动的幅频响应算子RAO值、辐射阻尼及附加质量。随着浮标吃水深度的增加，其垂荡方向RAO曲线峰值不断增大，且垂荡方向RAO曲线达到峰值的频率减小。当波浪频率ω≤0.4 rad/s时，浮标的纵荡RAO值最大，当吃水深度4.6 m≤H≤5.6 m时其RAO极值为H=6.1 m时的2.16倍。随着波浪频率增加，浮标纵荡和垂荡RAO曲线均趋近于0。在波浪频率较低(ω≤1.5 rad/s)海况时，吃水较浅的浮标系统可最大限度地减小竖直方向上的响应；而在波浪频率较高(ω≥3 rad/s)的海域，浮标的吃水深度对其运动响应影响不大。浮标纵荡辐射阻尼的峰值随着浮标吃水深度的增大而增大，且最大值对应的波浪频率与浮标吃水深度成反比；而垂荡辐射阻尼的峰值随着吃水深度的增大而减小，最大值对应的波浪频率与浮标吃水深度成反比。

表3 浮标不同吃水深度参数

从浮标纵荡和垂荡的附加质量随着吃水深度的变化曲线可知，浮标吃水越深，其纵荡附加质量越大。当波浪频率ω位于0～2 rad/s的区间时，纵荡附加质量随着频率的增加而增加，且不同吃水深度浮标之间的附加质量差值较大；当波浪频率ω从2～3.5 rad/s变化时，附加质量随着频率的增加而减小，且当频率ω=3.5 rad/s 时不同吃水深度浮标之间的附加质量差值达到最小。当波浪频率进一步增大时，纵荡附加质量进一步增大。对垂荡附加质量而言，除吃水深度H=6.1 m外，当波浪频率ω位于0～3 rad/s的区间时，附加质量随着浮标吃水深度的增加而减小，当波浪频率ω大于3 rad/s时，附加质量随着浮标吃水深度的增加而增大。整体附加质量的变化趋势随着波浪频率的增加先减小后增大。浮标垂荡固有频率受水线面面积与垂荡附加质量影响，水线面面积越小，垂荡附加质量越大，浮标垂荡固有频率越小。由图3中不同吃水垂荡辐射阻尼与附加质量变化结果可知，随着浮标排水量的增加，水线面面积减小，其垂荡方向固有频率不断减小，致使浮标垂荡方向RAO峰值频率不断减小。当浮标处于较深吃水H=6.1 m工况时，浮标水线面面积达到最小，浮标垂荡方向上辐射阻尼很小造成其在共振频率处具有较大的垂荡RAO幅值。

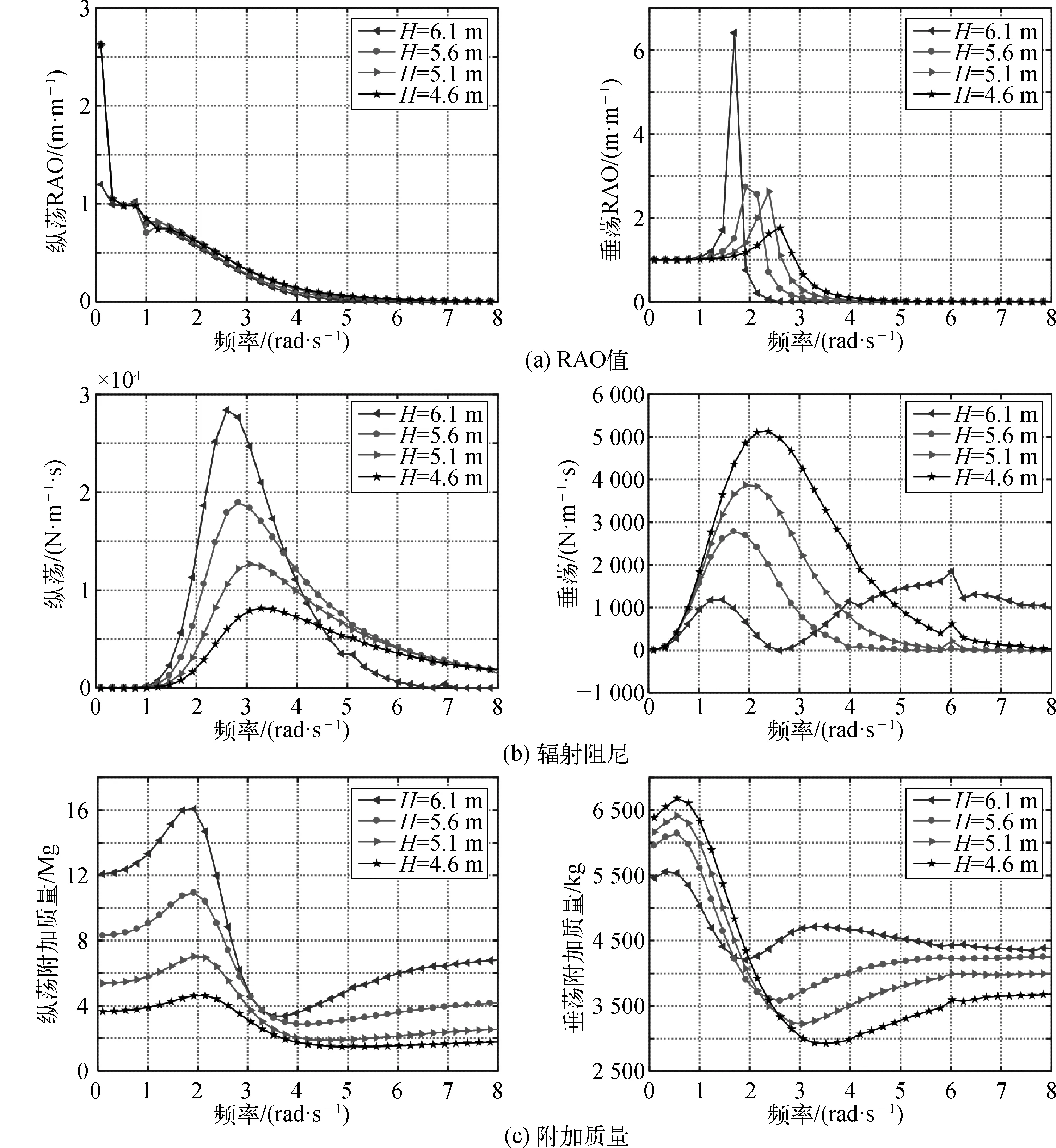
图3 不同吃水深度浮标水动力性能变化Fig. 3 Hydrodynamic performance with different buoy drifts

图4表示浮标所受一阶和二阶波浪力随吃水深度变化曲线。由图4可知，对于纵荡而言，浮标受到的一阶波浪力大小和吃水深度成正比，当波浪频率ω小于2.5 rad/s时，一阶波浪力随着波浪频率的增大而增大；当波浪频率ω大于2.5 rad/s时，一阶波浪力随着波浪频率的增大而减小并趋于0。浮标纵荡方向上受到的二阶波浪大小峰值随吃水深度增加先增大后减小再增大，对应峰值的频率不断减小。随着波浪频率的增加，二阶波浪力达到峰值后减小，随着波浪频率进一步增大，二阶波浪力趋于一恒定值。除H=6.1 m工况外，当波浪频率ω小于1.0 rad/s时，垂荡方向浮标所受到的一阶波浪力大小基本相同；当波浪频率ω大于1.0 rad/s时，一阶波浪力随着浮标吃水深度的增加而减小，整体上呈现随波浪频率增加而减小的趋势。对垂荡二阶波浪力而言，整体变化趋势为随着波浪频率的增大先增大后减小，除吃水深度H=6.1 m外，其余工况下的二阶波浪力值均较为接近。

图4 不同吃水深度下浮标水动力性能变化Fig. 4 Hydrodynamic performance with different buoy drifts

2.2 浮标形状对水动力性能的影响

考虑不同浮标倒圆台下部浮筒形状的影响，图5表示不同形状尺度参数的浮标形状模型示意图，固定浮标质量M为9 280 kg。形状参数定义为λ=D1/D2，其中D1为浮标倒圆台下部直径，D2为浮标主浮筒直径，不同浮标形状尺寸参数设置如表4所示。

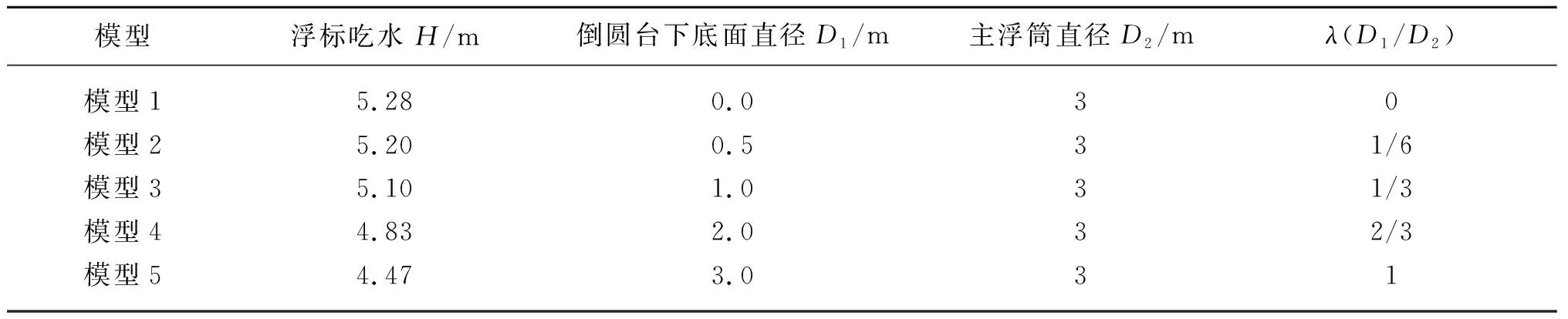
表4 浮标不同形状模型倒圆台浮筒下底面直径参数

图6为不同形状参数下浮标纵荡与垂荡的 RAO值、辐射阻尼及附加质量曲线。如图6所示，浮标形状参数对纵荡RAO值影响较小，浮标纵荡RAO值均随着波浪频率的增加而减小，当波浪频率大于0.3 rad/s时，纵荡RAO值出现陡降。与纵荡不同，浮标垂荡RAO值随波浪频率增加呈现先增大后减小的趋势，当λ=1时，浮标垂荡RAO值达到最大；当波浪频率大于4 rad/s时，浮标垂荡RAO值降为0。不同形状参数的浮标纵荡和垂荡辐射阻尼均随波浪频率的增大先增大后减小。值的注意的是，当形状参数λ=1时，浮标纵荡辐射阻尼峰值达到最大值，而垂荡辐射阻尼峰值最小；而当λ=2/3时, 垂荡辐射阻尼峰值达到最大。不同形状参数的浮标纵荡和垂荡附加质量均随波浪频率的增大先增大后减小再增大，且纵荡方向附加质量对浮标形状参数不敏感；当λ=1时，浮标垂荡附加质量达到最大，且明显大于其他形状参数工况。从图6浮标垂荡辐射阻尼与附加质量分析结果可知，不同形状浮标水线面面积相同，而形状参数λ=1时浮标垂荡自由度方向的辐射阻尼较小，附加质量达到最大，造成该形状浮标在垂荡方向上固有频率较小，共振频率处响应幅值较大。

图6 不同形状浮标水动力性能变化Fig. 6 Hydrodynamic performance with different buoy shapes

图7表示不同形状参数下浮标纵荡与垂荡波浪一阶和二阶波浪力随波浪频率的变化曲线。如图7所示，除λ=1/6外，浮标纵荡一阶波浪力峰值随浮标形状参数λ的增加而增大，且峰值对应的波浪频率也逐渐增大；当波浪频率ω小于2.5 rad/s时，不同形状浮标的一阶波浪力基本一致。浮标纵荡二阶波浪力整体趋势随着波浪频率增加先增大后减小，当波浪频率ω大于4 rad/s后，不同形状的浮标二阶波浪力趋于一恒定值。对于垂荡而言，浮标一阶波浪力随形状参数λ变化较小，随着波浪频率增加而不断减小至0。不同形状参数的浮标垂荡二阶波浪力均随着波浪频率增加先增大后减小，当λ=1时，浮标垂荡二阶波浪力达到最大值，且明显大于其他形状参数。

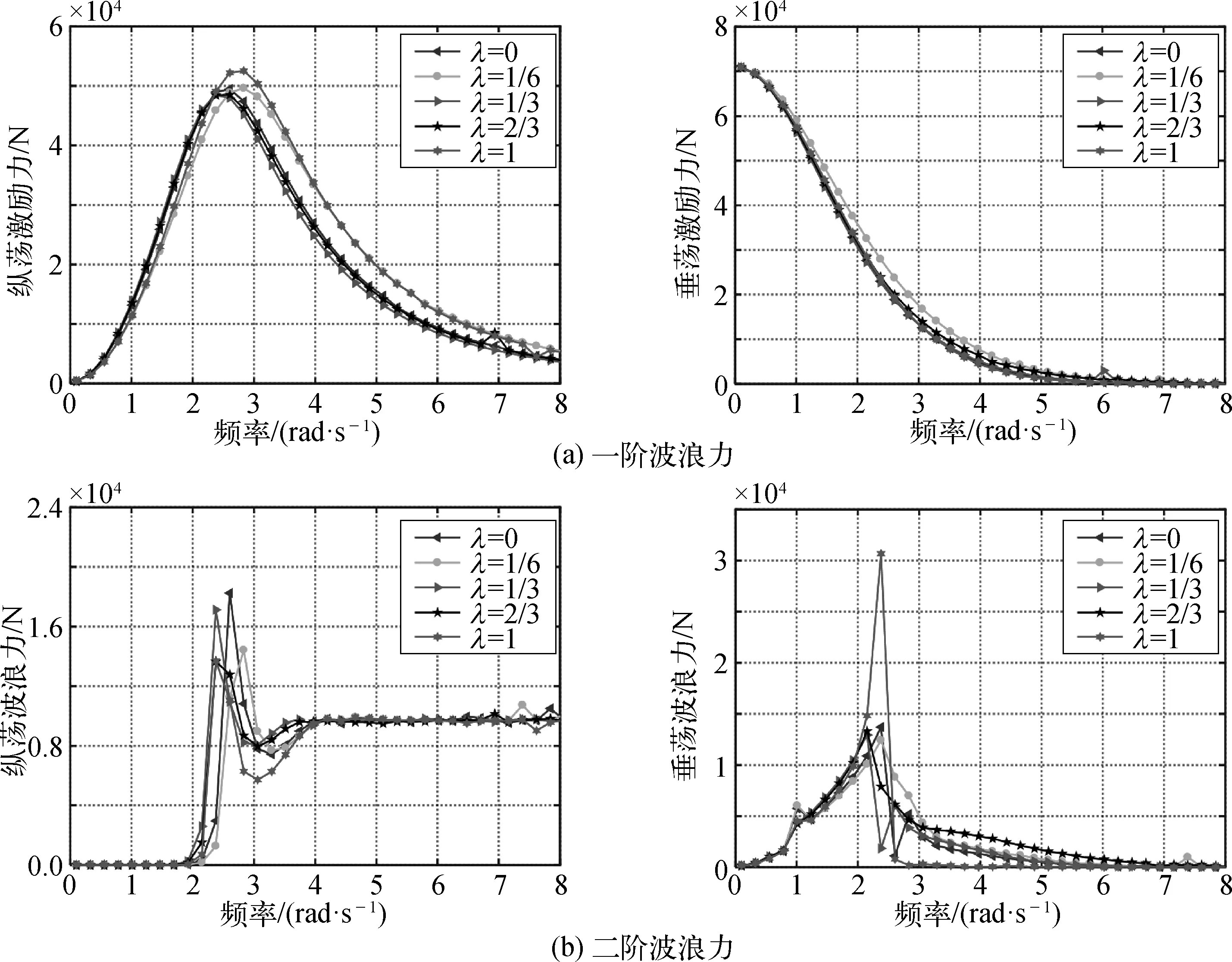
图7 不同形状参数下浮标水动力性能变化Fig. 7 Hydrodynamic performance with different buoy drifts

3 激光雷达浮标锚泊系统分析

3.1 时域运动响应分析

选取吃水深度H为5.1 m, 形状参数λ为1/3的激光雷达浮标，对其在百年一遇海况下的时域运动响应特性进行了分析。浮标布放海域百年一遇海况选取风速为31.6 m/s，表层流速为1.48 m/s，波浪谱选择Jonswap谱，有效波高为9.4 m，谱峰周期为15.2 s，谱峰因子取3。风浪流载荷方向α取最危险的同向工况，从0°到90°变化分布，具体环境参数如表5所示。

表5 生存工况环境条件

为保证激光雷达浮标在百年一遇海况环境条件下的生存能力，需要对其系泊系统张力进行校核。图8～9分别为不同环境载荷入射角度下锚链顶端张力时程曲线和运动偏移距离时程曲线，表6为系泊锚链在相应工况下锚链张力变化的统计值。从图9中可以看出，当环境载荷顺延锚链所在平面入射时，锚链1和锚链2受力会有极端张力值出现，该极端张力可以达到张力均值的十多倍；对比分析图8和图9结果，可以发现锚链1、2张力变化出现极端值的时刻分别为激光雷达浮标在x方向偏移距离出现最大值和最小值的时刻。从表6的统计结果可知，在各工况下锚链安全系数均大于CCS规范[24]要求的安全系数1.67，符合规范要求。当环境载荷入射角度α=0°时，锚链1处于迎浪向，锚链1的张力大于锚链2。随着入射角度增大，锚链2张力均值逐渐增大。锚链1和锚链2张力峰值在α=0°时出现最大值，当α=45°时，锚链1和锚链2时程曲线张力峰值均较小。当α增大到90° 时，锚链1和锚链2同时承受对称分布荷载，锚链张力均值进一步增大。

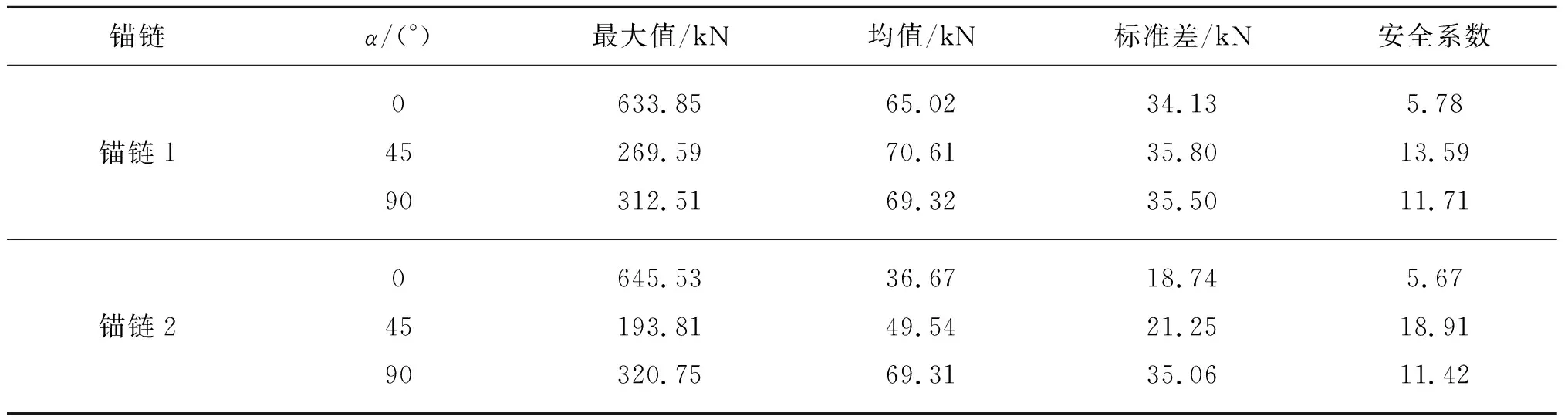
表6 不同入射角度锚链张力统计值

图8 不同入射角度锚链张力时程曲线Fig. 8 Time history of tension for two mooring chain at different incident angles

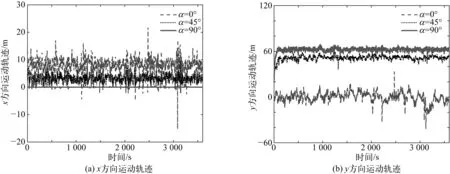
图9 不同入射角度浮标运动轨迹Fig. 9 Tension time history of buoy trajectory at different incident angles

从图9的运动偏移距离曲线结果可以看出，当入射角度α从0°到90°变化时，浮标在x方向上的偏移距离逐渐减小，在y方向上的偏移距离不断增大，α=0°时浮标y方向上的偏移距离在0附近变化，而α=90°时浮标x方向上的运动偏移距离在0附近变化。由于锚链1的初始布置方向为沿着x轴方向，在α=0°入射时，浮标在x方向上的偏移最剧烈，锚链1处于被拉伸状态，其张力均值最大；当α逐渐增大到45°时，锚链1的拉伸程度减弱导致其张力均值减小，锚链2张力均值增加；当α进一步增大到90°时，浮标在y方向上的偏移距离最大，锚链1和锚链2均处于拉伸状态，其张力均值基本相等。值得注意的是，当α从0°到90°变化时，锚链1张力变化标准差基本保持在稳定值，而锚链2张力变化标准差逐渐增大。

图10表示对不同环境载荷入射角度下锚链顶端张力时程曲线进行快速傅里叶变换得到的张力谱结果。如图10所示，对于迎浪向的锚链1而言，其张力在频率区间为0.3～1.26 rad/s内具有较大的响应幅值，而在频率为1.70 rad/s时取得张力幅值的极值，且随着环境载荷入射角度从0°至90°变化，张力极值呈现先增大后减小的变化趋势。对于锚链2而言，其位于0.3～1.26 rad/s频率区间内的张力幅值以及极值均随环境载荷入射角度增大而增大。对比锚链1与锚链2的谱分析结果可知，当锚链处于与环境载荷入射角度小于90°的范围内，迎浪向锚链张力响应剧烈程度显著大于逆浪向锚链张力响应。

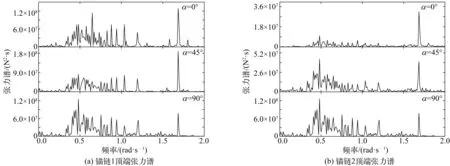
图10 不同入射角度锚链张力谱Fig. 10 Spectrum curve of tension for two mooring chains at different incident angles

由此可见，当环境载荷与两点式系泊系统锚链所在的平面平行入射时，可能会发生锚链张力极端变化的情况。与前人关于锚链运动的实验研究结果[25-28]类似，当浮式结构受到上部与锚链方向同向的周期性激励时，若锚链被带动发生从松弛到张紧状态的循环变化时，可能发生锚链极端张力变化。

3.2 锚链极端张力特性分析

进一步开展了不同波浪要素参数下激光雷达浮标系泊锚链张力的变化特性研究。风、浪、流同向取0°角入射，风速和流速分布均保持不变，如表7所示。波浪谱取Jonswap谱，有效波高从3.0～9.4 m变化，谱峰周期从15.2～18.2 s变化，谱峰因子均取3，具体工况参数见表7。

表7 波浪参数变化

图11～14分别为不同有效波高与谱峰周期工况下激光雷达浮标系泊锚链张力变化时程曲线。表8～9分别为相应工况下张力变化统计值。如图所示，当有效波高Hs从3 m到9.4 m变化时，锚链1和2张力时程曲线出现明显的峰值，随着有效波高增大，锚链1和2张力逐渐增大；当Hs=9.4 m时，锚链1和2出现较明显的极端张力值，锚链1和锚链2极端张力值与均值的比值分别达到9.74和14.40。除有效波高Hs为3 m 和7 m的工况外，锚链2出现不同程度的极端张力峰值，且锚链2的极端张力出现频率更高。锚链1、2张力变化标准差均随着有效波高增加而增加，说明有效波高越大，其张力变化越剧烈。

表8 不同有效波高的锚链张力统计值

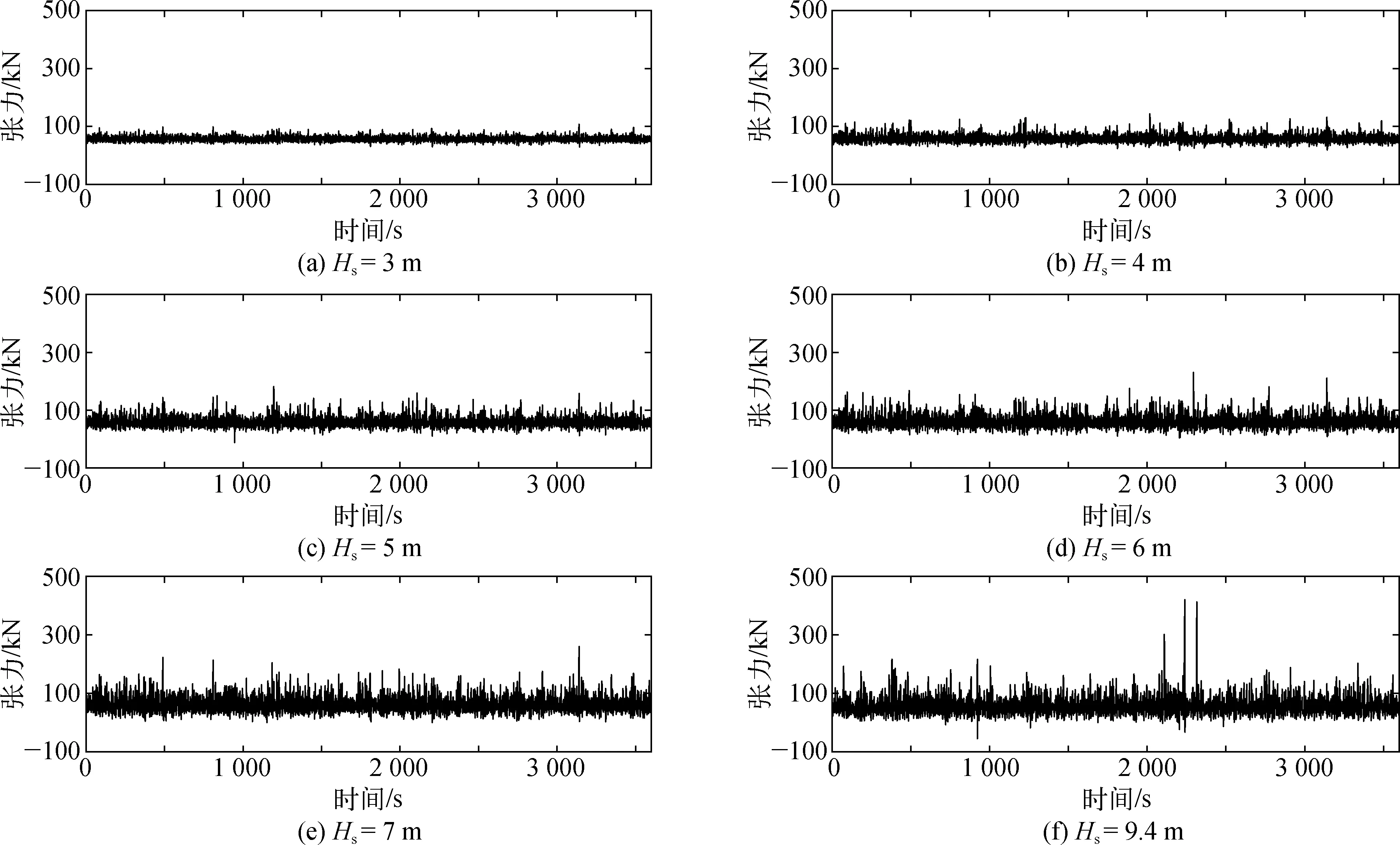
图11 不同有效波高工况锚链1张力时程曲线Fig. 11 Time history of tension for mooring chain 1 with different significant wave heights

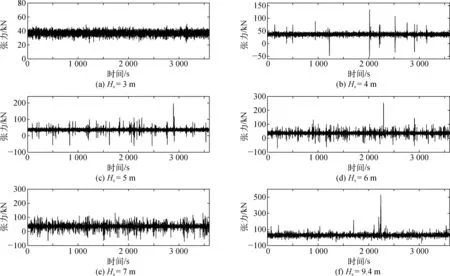
图12 不同有效波高工况锚链2张力时程曲线Fig. 12 Time history of tension for mooring chain 2 with different significant wave heights

图13 不同谱峰周期工况锚链1张力时程曲线Fig. 13 Time history of tension for mooring chain 1 with different wave spectrum peak periods

图14 不同谱峰周期工况锚链2张力时程曲线Fig. 14 Time history of tension for mooring chain 2 with different wave spectrum peak periods

通过分析图13～14和表9可知，当波浪谱峰周期逐渐增大时，锚链1、2张力的均值逐渐减小，张力变化减弱。当波浪谱峰周期Tp处于15.2～17.0 s区间时，锚链1出现明显的极端张力，而随着谱峰周期的增大，张力均值不断减小，极端张力出现的概率明显降低。对比锚链2张力变化时程曲线结果可知，锚链2在谱峰周期Tp为15.2 s、15.8 s、17.0 s 的工况均出现了极端张力，谱峰周期越小，其锚链出现极端张力值也越大。综上所述，当锚链受到风浪流环境载荷作用发生松弛与张紧状态的循环往复变化时，锚链在短时间内由于受到冲击作用出现张力急剧增大的现象，且受波浪要素变化影响较大。

表9 不同谱峰周期锚链张力统计值

浮标纵荡运动响应谱与入射波谱的对比分析结果如图15和表10所示，当锚链方向与波浪入射同向时，浮标纵荡运动显示明显的低频特性，其中0～0.5 Hz的贡献占主导地位，这是因为浮标系统纵荡方向回复力较小，自然频率较低，在二阶波浪力的作用下发生了大幅度的低频慢漂运动。入射波峰频范围内出现运动谱峰峰值，随着入射波谱峰周期的增加，纵荡谱峰频逐渐减小，可以看到除发生极端张力的工况外，纵荡波频运动响应在谱峰周期为16.4 s、17.6 s和18.2 s工况时峰值较小，对应表9中相应谱峰周期工况锚链最大张力值较小。

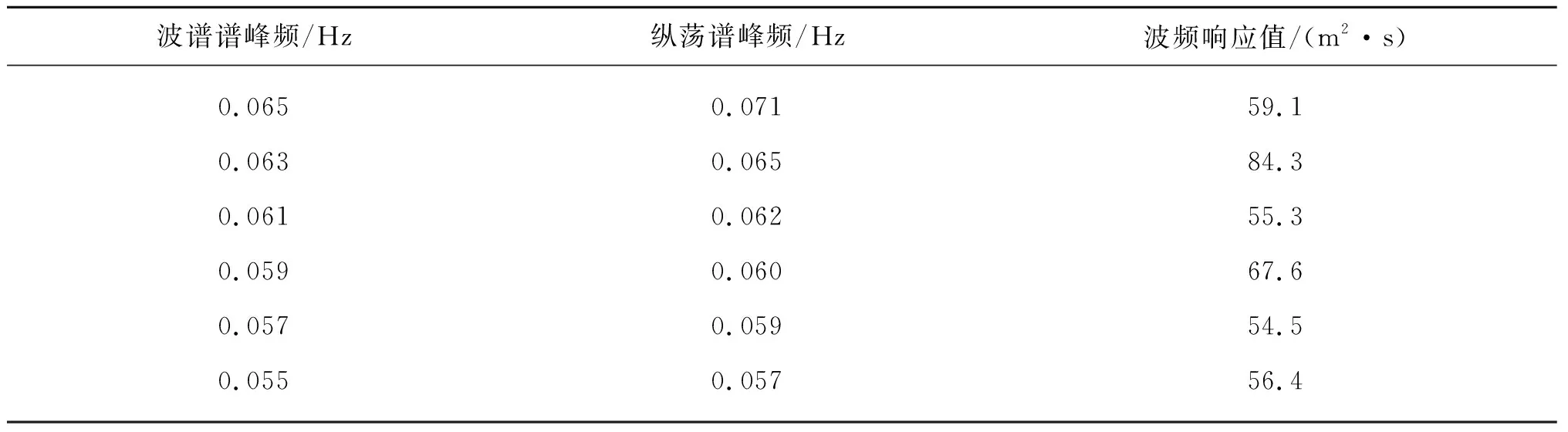
表10 波谱与纵荡谱峰频对比

图15 不同谱峰周期下浮标运动响应谱与波谱的比较Fig. 15 Comparison of motion response spectrums with incident wave spectrum for different wave Tps

4 结 语

针对新型激光雷达浮标开展了水动力性能及锚泊系统张力特性数值研究，揭示了浮标吃水深度、形状参数对于激光雷达浮标运动响应以及风浪流入射角度对其系泊张力特性的影响规律。得到的主要结论如下：

1) 随着浮标吃水深度的增加，浮标纵荡运动响应变化不明显，一阶波浪力与二阶波浪力均显著减小；浮标垂荡方向运动响应与二阶波浪力均随着浮标吃水深度的增加而增大，而一阶波浪力呈减小变化趋势。随着浮标底部圆台直径的增大，浮标纵荡运动响应、一阶波浪力和二阶波浪力均无明显变化；浮标垂荡方向运动响应随浮标底部圆台直径的增大而增大，一阶波浪力变化则较小。此外，圆柱形浮标所受垂荡二阶波浪力显著大于圆台形浮标。

2) 不同风浪流入射角度下，浮标迎浪向锚链张力变化剧烈程度大于逆浪向锚链；当波浪荷载与锚链同一平面入射，致使系泊锚链发生松弛与张紧状态的循环变化时，会在短时间产生锚链张力急剧增大现象，对浮标系统产生极大的冲击载荷作用，进一步会影响系泊系统疲劳寿命和浮标系统整体安全。

3) 锚链极端张力受波浪要素变化影响较大，随着波浪有效波高增大，锚链极端张力幅值与出现频次均显著增加；随着波浪谱峰周期减小，锚链极端张力幅值与出现频次也显著增加。