风、浪荷载作用下海上风机单桩结构灌浆连接段疲劳性能评价

黎亚舟，王 衔, ，陈 涛，顾祥林

(1. 中交第三航务工程局有限公司，上海 200032；2. 同济大学 工程结构服役性能演化与控制教育部重点实验室，上海 200092)

单桩支撑结构作为最为流行的海上风电基础形式，截止2019年，单桩结构形式占整个欧洲所有已装机的海上风电基础的81%[1]。单桩与上部结构连接主要的手段是灌浆连接，其技术的原理是通过在内外钢管间的环形间隙中填充高性能灌浆料的方式来连接直径不同的过渡段和钢管桩。随着7～10 MW级风电机组技术的发展，风机叶轮半径和重量的增加对基础支撑结构安全性能提出了更高的要求。海上风电支撑结构在20年使用寿命期间需承受高达109次风、浪荷载作用[2]，因此其疲劳性能尤为重要。

灌浆连接段最早的应用出现在20世纪70年代海洋石油燃气平台导管架结构中，当时的学者对灌浆连接段的轴向静力极限承载力的关注远高于疲劳性能，同时期只有少数学者[3-6]关注灌浆连接的轴向疲劳强度。这里以单桩支撑结构作为研究对象，其灌浆连接段主要受到弯矩作用，轴向荷载变化较小。对于灌浆连接段的弯曲疲劳性能，近20年来许多学者也进行了相关的试验研究[7-9]，并依据相关试验结果对灌浆连接段设计规范[10]进行了相关修订。

基于385种工况下的广东某实际5 MW单桩风机支撑结构在风、浪荷载作用下的动力响应分析，获取了灌浆连接段荷载边界条件时程。建立灌浆连接段精细化有限元子模型，将荷载边界条件转化为应力时程。对于剪力键采用“热点应力”方法进行疲劳性能评价。对于灌浆材料，选取剪力键附近灌浆材料单元积分点处的第三主应力进行疲劳性能评价。采用Palmgren-Miner线性损伤累计准则和雨流计数方法进行疲劳损伤的累计。

1 某实际5 MW单桩支撑结构在风、浪荷载作用下的动力响应

图1给出了某5 MW海上风机单桩结构示意图及实地场地条件，其主要设计参数如表1所示。结合广东省某地一年内的实际风、浪实测数据，运用谱表达法模拟生成了385种工况下单桩风机结构上的随机风、浪荷载时程，主要包括风机运行气动荷载、风机塔身风荷载、波浪荷载。为简化计算，较为保守地将所有荷载作用在同一平面内。

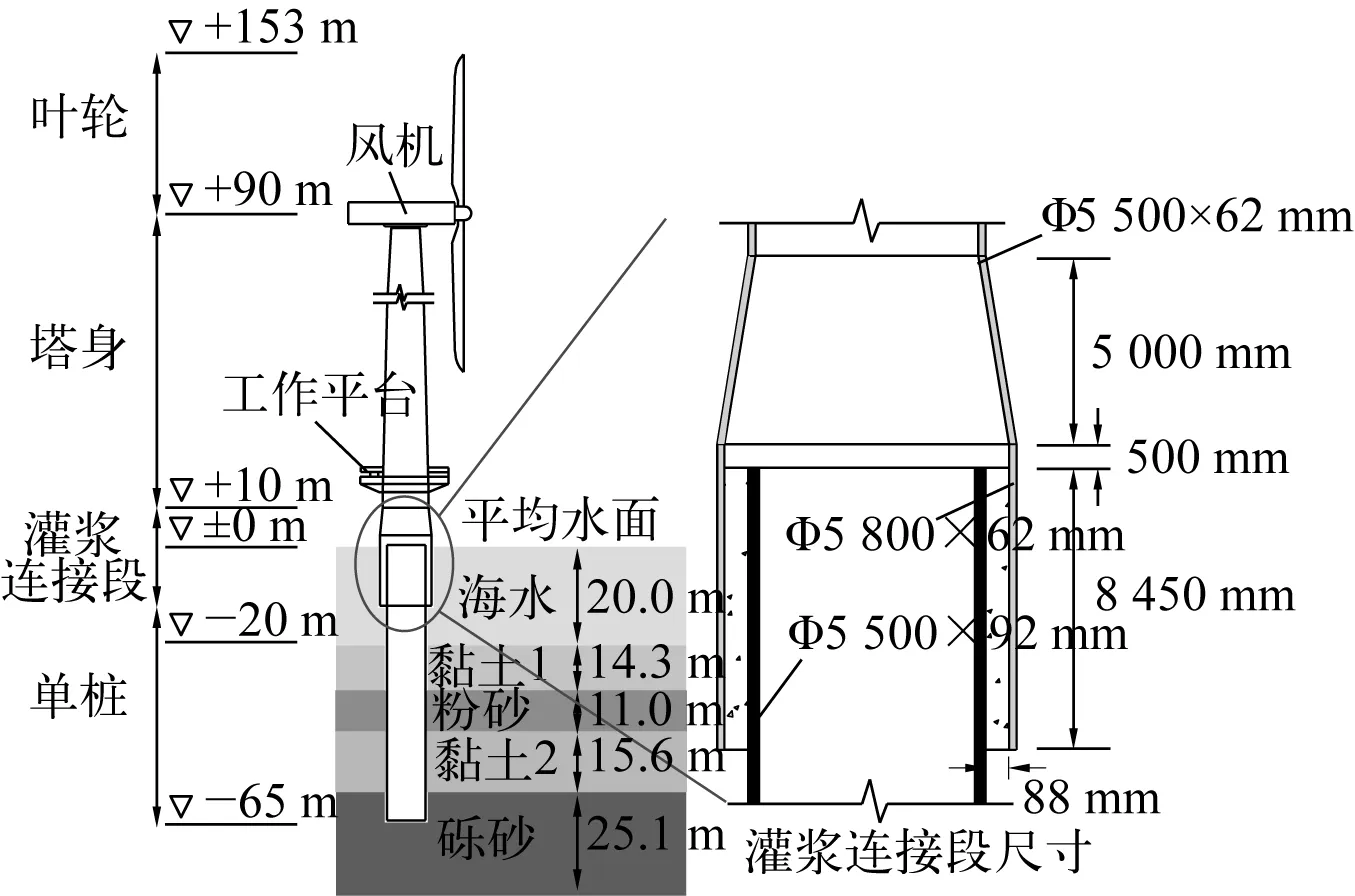
图1 某实际5 MW单桩支撑结构及实际场地条件Fig. 1 Real 5 MW monopile structure and soil condition

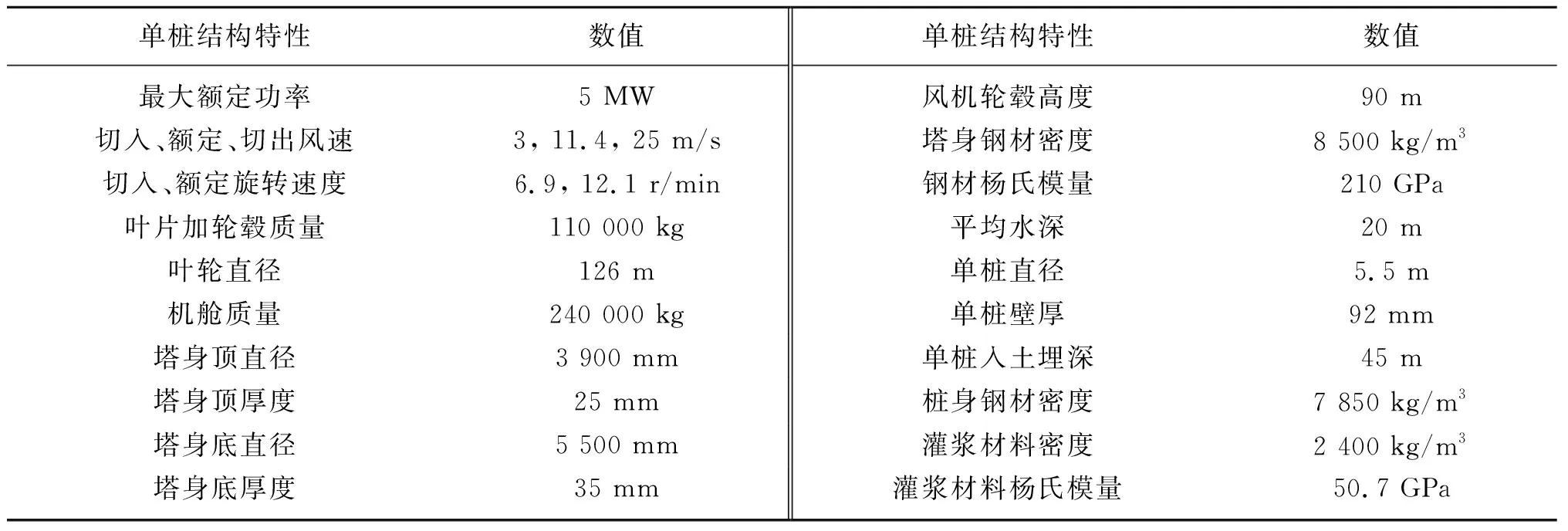
表1 某实际5 MW海上风机单桩结构设计参数

建立了综合考虑桩—土相互作用、灌浆连接段影响以及多种工况下不同阻尼比的实际单桩支撑结构的动力响应模型。实现了385种风浪耦合工况下的单桩支撑结构的时域动力响应分析及灌浆连接段的荷载边界条件时程的提取，如图2所示。此部分在文献[17]中叙述，文中不再详述。

图2 单桩支撑结构动力分析及荷载边界条件提取Fig. 2 Dynamic analysis and load boundaries extraction

2 某实际灌浆连接段精细化有限元模型

采用Abaqus软件进行建模，建立的灌浆连接段精细化有限元模型如图3所示，详细的建模方法可参见文献[18]。该模型采用导管架灌浆连接段轴压试验以及单桩结构灌浆连接段疲劳后轴向静力试验的相关结果进行了验证，详见文献[19]，在此都不再赘述。通过此精细化有限元模型可将灌浆连接段的荷载边界条件时程转化为应力的时程。

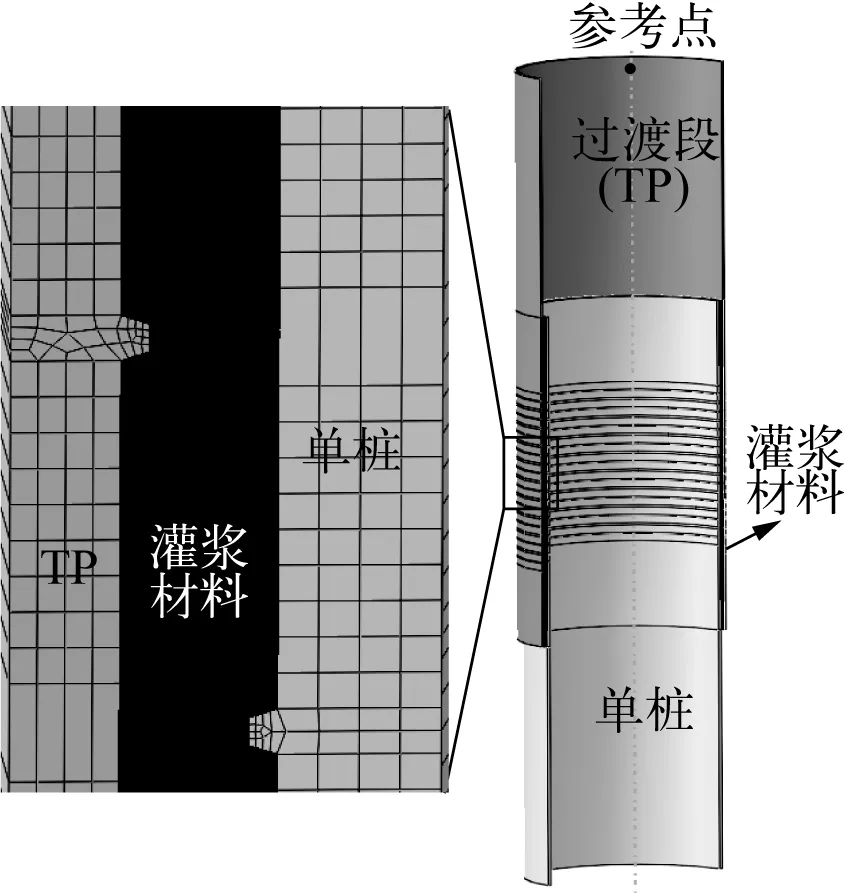
图3 灌浆连接段精细化有限元模型Fig. 3 Refined finite element models for grouted

按照图1中尺寸建立某实际单桩风机结构中灌浆连接段有限元模型。其中剪力键布置在灌浆连接段中间1/2长度内，间距s=450 mm，剪力键高度h=16 mm，剪力键宽度w=26 mm。剪力键的编号如图4所示。钢管和灌浆材料的材料属性取某次材性试验的实测值，如表2所示。

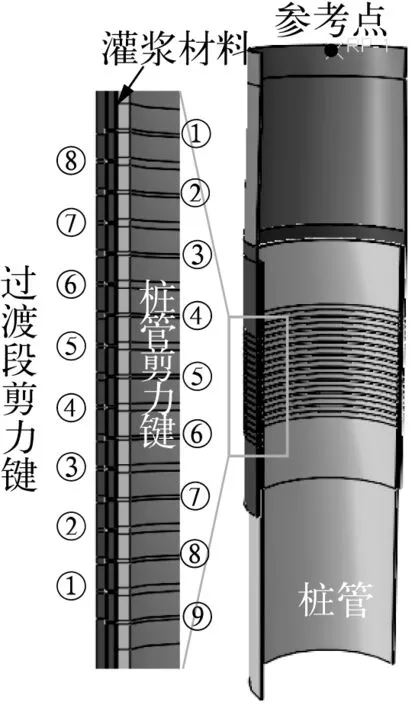
图4 某实际灌浆段内剪力键编号Fig. 4 The numbers of shear keys in the real grouted connection

表2 某实际灌浆连接段材料性能参数

3 灌浆连接段疲劳性能评价方式

灌浆连接段是由钢结构和灌浆材料组成的组合结构，故其疲劳性能评价应当分成钢结构、灌浆材料两部分叙述。本节将从这两方面介绍灌浆连接段性能的评价方式，并补充介绍DNVGL-ST-0126规范[20]提出的建立在其承载力理论公式基础上的灌浆连接段整体结构疲劳性能评价方式。

3.1 Palmgren-Miner线性损伤累计准则

Palmgren-Miner线性损伤累计准则是疲劳分析中最常见的损伤累计方法，其假定所有k种工况下的结构或构件的总损伤值D是每种工况下损伤值的累加之和，即：

(1)

其中，ni是第i种工况出现的次数，可采用文献[21]附录A中所述方法对数据进行过滤，并通过雨流计数法进行统计，相关介绍可参见文献[22-23]，雨流计数法采用的是美国材料与试验协会(ASTM)标准“E 1049-85”[24]中5.4.4节规定的；Ni是第i种工况下的疲劳寿命。一般假定构件或结构的总损伤值D低于某一特定限值时就不会发生疲劳破坏。

3.2 焊接剪力键的疲劳性能

灌浆连接段内通常可能出现钢材疲劳破坏的位置为焊接剪力键附近，因此，采用“热点应力”法预估此灌浆连接段内钢管焊接剪力键的疲劳寿命。不同规范对于“热点应力”的计算方式定义一般略有差异，采用DNVGL-RP-C203[25]建立焊缝处的几何有限元模型，取出距离焊趾0.5t和1.5t(t为焊接母材厚度)位置处的“几何应力”，通过线性插值即可得到焊趾处的“热点应力”。

如图5所示，平行焊缝方向的正应力可用σP表示，平行于焊缝方向的剪应力可用τP表示，而垂直于焊缝方向的正应力可用σV表示；图中“Δ”符号代表应力分量的变化值即应力幅。距离焊趾位置0.5t和1.5t处“几何应力”的应力幅可按下式计算：

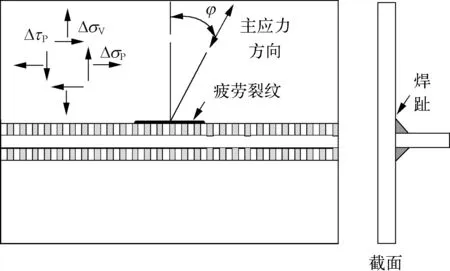
图5 焊缝应力的示意Fig. 5 Stress components around the welded toes

(2)

其中，Δσ1表示焊缝平面内最大主应力幅，表示Δσ2焊缝平面内最小主应力幅，则有：

(3)

(4)

参数α的取值，规范[25]附录表A-3详细规定了焊缝的分类方法和等级评定，当考虑剪力键焊缝为手工焊缝这种最不利情况时，参数α取为0.90。

得到上述距离剪力键焊趾0.5t及1.5t处的应力分量后进行线性插值，即可以得到焊趾处(即0t处)的应力分量，计算所有应力分量的变化幅度，根据式(2)计算焊趾处的“几何应力”(即“热点应力”)的应力幅Δσeff_0t。

得到焊趾处的“热点应力”的应力幅Δσeff_0t后，根据规范[25]的2.4.3节相关规定，若考虑焊接母材厚度的影响，则钢管焊接剪力键的疲劳寿命与“热点应力”的应力幅之间的关系可以用式(5)的S-N曲线表示。

(5)

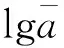
同时，规范[25]中规定，当焊接结构无法监测及维修时，式(1)中的总损伤值D的限值为1/3。

3.3 灌浆材料的疲劳性能

DNVGL海上混凝土结构设计规范DNVGL-ST-C502[26]中给出的混凝土或灌浆材料的S-N曲线，其表达式如式(6)所示。

(6)

式中：frd为材料破坏时的抗压强度；C1为参数，在空气中的结构取为12.0；水中受压—压循环时取为10.0，受拉—压循环时取8.0。

(7)

式中：γm为材料分项系数，对有剪力键灌浆连接段疲劳分析时取为1.5；fcn为灌浆材料场地的抗压强度，按式(8)计算。

(8)

其中，fcck为灌浆材料抗压强度代表值，由150 mm直径，300 mm高度圆柱体试块测得；σmax为应力循环中的最大压应力；σmin为应力循环中的最小压应力，当为拉应力时取为0；C5为疲劳强度参数，对混凝土可取为1.0，对灌浆材料需要通过试验确定，当无试验时取为0.8。

如果式(6)计算所得的lgN大于式(9)中X值，则此计算值须乘以式(10)中参数C2。

(9)

C2=[1+0.2(lgN-X)]>1.0

(10)

与焊接结构的规定类似，规范[26]中也规定当焊接结构无法监测及维修时，式(1)中的总损伤值D的限值为1/3。

由于剪力键局部区域存在较为严重应力集中，灌浆连接段中的灌浆材料的裂纹一般始于剪力键位置。因此，将灌浆材料的疲劳性能计算位置定在如图6所示的剪力键局部区域上方和下方的单元；利用单元积分点的第三主应力和上述灌浆材料的S-N曲线评价灌浆层的疲劳寿命。

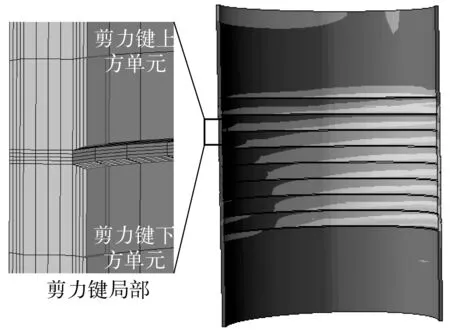
图6 有限元模型灌浆层剪力键区域计算疲劳性能位置Fig. 6 Location for calculation of fatigue property of grout material

3.4 灌浆连接段的整体疲劳性能

DNVGL-ST-0126规范[20]给出了灌浆连接段的整体疲劳性能分析方法，该方法建立在其推导的灌浆连接段承载力理论公式[8,27]基础上，定义y为某一荷载循环下，单位长度的单层剪力键上所受荷载FV1Shk和剪力键承载力设计值FV1Shk, cap的比值，即

(11)

式中：γm为材料参数，对有剪力键灌浆连接段疲劳分析时取为1.5。

则在此荷载循环下灌浆连接段的疲劳寿命N为

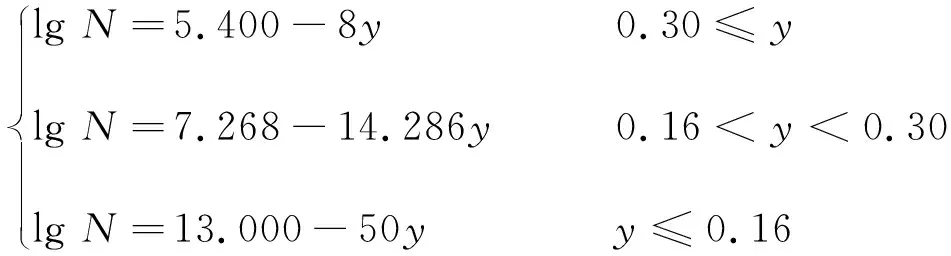
(12)

然而该疲劳寿命曲线只建立在有限的试验数据基础上并且保守地取为试验数据的下包线，无法准确预测灌浆连接段疲劳寿命，后文的计算结果将进一步说明该曲线的保守性。

4 风、浪荷载作用下灌浆连接段疲劳性能评价

4.1 灌浆连接段荷载边界条件的简化

经过对提取的灌浆连接段实际荷载边界条件进行统计，顶部轴力FV1最大值为6 472.6 kN，最小值为6 469.6 kN，变化范围很小，同样底部轴力FV2最大值为8 525.7 kN，最小值为8 522.4 kN。因此可将轴力简化为固定值，取顶部轴力FV1为6 475 kN。采用图4所示的半模型，顶部轴力值为3 237.5 kN，忽略灌浆连接段上部过渡段钢管的重量，保守地将该轴力直接施加在半模型顶部的参考点上。

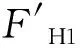
图7 灌浆连接段边界条件的简化Fig. 7 Simplification of the load boundary conditions

(13)

(14)

4.2 灌浆连接段精细化有限元模型确定应力分布

4.2.1 弯矩和水平力作用下的应力叠加

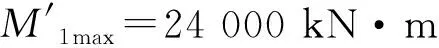
在最大弯矩荷载和水平力同时作用下桩管的最大Mises应力出现在图4中的⑨号剪力键处，最大值为49.89 MPa，仍处于弹性状态。过渡段钢管的最大Mises应力出现在图4的⑧号剪力键处，最大值为75.99 MPa，也处于弹性状态。灌浆材料第三主应力最大值出现在桩管侧⑧号剪力键附近，最大值为25.27 MPa，小于最大受压强度87.6 MPa的1/3，处于弹性状态。由于所有部件仍处于材料的弹性阶段，因此可以考虑进行弯矩荷载和水平力分别作用下的叠加。

对三种工况下的应力状态最大值位置的应力进行提取，如表3所示。

表3 某实际灌浆连接段材料性能参数

将三种工况下的桩管、过渡段、灌浆材料的最大应力值分别减去轴力和自重作用下的应力值，以弯矩和水平力共同作用下的工况作为基准，利用弯矩和水平力分别作用时两种工况的加和减去基准值后，再除以基准值，可得到弯矩和水平力分别作用下的最大应力直接叠加产生的误差。从表3中可知，除去重力和轴力荷载后，灌浆材料和桩管内部最大应力值直接叠加的误差均在2%左右，而过渡段内部最大应力直接叠加的误差也仅在8.5%以内。同时，由于三种工况是所有弯矩和水平荷载的最大包络值，由此可以认为在此范围内的随机弯矩和水平力荷载作用下的应力状态可以进行叠加。

4.2.2 弯矩和水平力单独作用下的应力分量的提取

通过Abaqus后处理文件，分别提取除去重力和轴力荷载后，弯矩或水平力单独作用下灌浆连接段内部的应力分量与荷载大小间的关系。由于假定水平力和弯矩荷载都只作用在灌浆连接段的对称面上，因此应力最大的截面必然出现在对称面上，因而只需考虑对称面上的应力分量即可。

对于钢管上的焊接剪力键，如图8所示，按照3.2节所述的方法计算热点应力时，需要距离焊趾0.5t和1.5t位置的应力分量，即同时提取图8中剪力键焊趾上方和下方的②号、③号、⑦号和⑧号节点的应力分量，从而插值得到所需位置的应力分量。

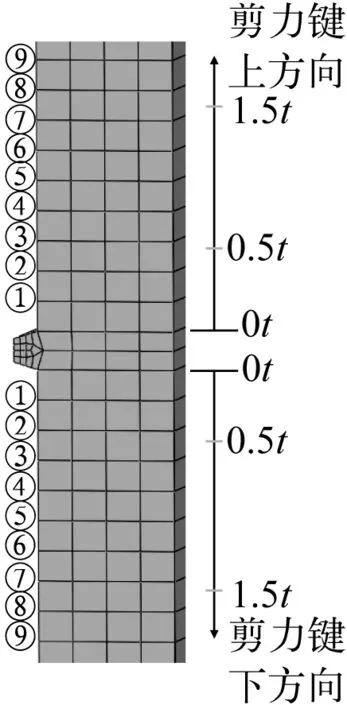
图8 剪力键局部网格及应力分量提取 Fig. 8 Stress components extraction around the shear key

对于灌浆材料，如3.3节所述，提取剪力键上方和下方最外层单元积分点处的第三主应力分量。

考虑到灌浆连接段内剪力键数量较多，且需提取不同荷载水平下的应力分量，因此利用Python语言编写Abaqus后处理程序，分别提取水平力和弯矩荷载分别作用下，灌浆连接段内剪力键附近钢管应力分量和灌浆材料第三主应力随荷载值变化的情况。

4.3 焊接剪力键疲劳性能评估

结合已经得到的灌浆连接段的荷载边界条件时程，以及除去重力和轴力荷载后，水平力和弯矩荷载单独作用下灌浆连接段内剪力键局部钢管应力分量与荷载值的关系；编写Matlab程序，通过荷载和应力的关系插值，转化为距焊趾0.5t和1.5t位置的应力分量时程。最后通过线性插值，得到钢管剪力键焊趾处热点应力分量的时程。

值得注意的是，3.2节所述的焊接剪力键疲劳性能“热点应力”评价方法相关计算时只考虑应力分量的变化幅值，而无需考虑应力分量的平均值，因此无需考虑重力和轴力荷载对应力分量平均值的影响，可直接采用除去重力和轴力荷载后的应力分量时程。

假定焊接剪力键为手工焊接，考虑水中并有阴极保护的S-N曲线，并将数据过滤的幅度定为“热点应力”应力幅Δσeff_0t的1/200。若某种工况下焊趾处的损伤值为di，其持续的时间为ti，发生的概率Pi，若假定海上风机单桩支撑结构的使用寿命T为20年，则依据线性损伤累计方法，某一剪力键位置处的总损伤D为各种工况下损伤Di的叠加：

(15)

经过计算后所有剪力键的最大损伤值D为1.349 8×10-10，出现在图4中过渡段受压侧最上方的⑧号剪力键上方焊趾处。此损伤值远小于3.2节规定的限值1/3，证明灌浆连接段在假设的20年的使用寿命中，焊接剪力键焊趾处不会发生疲劳破坏。

4.4 灌浆材料疲劳性能评估

与焊接剪力键疲劳性能评估思路类似，编写相应的Matlab程序，通过荷载和应力的关系插值，将荷载边界条件时程转化为剪力键局部灌浆材料第三主应力分量时程。

值得注意的是，与焊接剪力键疲劳损伤计算不同，3.3节的灌浆材料的S-N曲线相关计算时同时考虑应力分量最大值和最小值，因此需要考虑重力和轴力荷载对应力分量平均值的影响。读取重力和轴力荷载下的应力分量，直接叠加在弯矩和水平力荷载时程计算得到的应力分量时程上。

假定灌浆材料圆柱体单轴抗压强度为实测值87.56 MPa，并且参数C5取为0.85；材料分项系数取为1.5；在水中但只有压—压循环，则式(6)中参数C1取为10。同样，将Markov过滤的幅度定为应力分量幅度的1/200，经过式(15)计算后所有剪力键附近的灌浆材料的最大损伤值D为0.001 54，出现在图4中过渡段受压侧最上方的⑧号剪力键下方处，此损伤值大于焊接剪力键的最大损伤值，证明灌浆连接段在风、浪疲劳荷载下，灌浆材料疲劳起控制作用。然而灌浆材料损伤值D依旧在2‰之内，远小于3.3节规定的限值1/3，即在假设的20年的使用寿命中，灌浆连接段不会发生破坏。

分析上述所有工况下，起控制作用的过渡段受压侧最上方的⑧号剪力键下方灌浆材料的损伤值Di，取出排名前十的工况，如表4所示。从表中可知，前十位的工况风速均为12 m/s，此时风速最接近于5 MW风机运行的额定风速11.4 m/s，风机以额定风速运行时产生的推力最大。将损伤值Di前五位的工况的风、浪功率谱以及单桩风机结构基频都进行标准化处理后，绘制在图9中。从图中可知，Kaimal风谱峰值仍距离风机结构基频较远；而产生损伤值Di较大的前两种工况的B-M海浪谱的峰值也并非最为靠近结构基频，反而排名第三的Hs=1.25 m，Ts=5.005 s的工况的峰值频率更加接近结构基频，因此得出如下结论:海浪谱的峰值频率与结构基频越接近并不会对灌浆连接段产生越大的损伤值。

表4 过渡段受压侧最上方的⑧号剪力键下方灌浆材料损伤Di前十位的工况

图9 灌浆材料损伤Di的前五位不同工况下风 、浪荷载谱和结构基频的关系Fig. 9 Wind and wave spectrum under the 5 load conditions with the largest damage values

4.5 灌浆连接段整体疲劳性能评价

依据3.4节中所述的DNVGL-ST-0126规范[20]对灌浆连接段整体疲劳性能的评价方法，进行了相关计算。

假定设计中采用的灌浆材料75 mm立方体抗压强度为130 MPa；钢材杨氏模量为206 GP，泊松比为0.3；灌浆材料杨氏模量为50 GPa。将数据过滤的幅度定为式(11)中y值的1/200，则经过计算后发现，排名前9的工况损伤值Di都大于1，总损伤值D更是达到38.62。说明按照3.4节所述的规范[20]对灌浆连接段整体疲劳性能的评价方法计算，灌浆连接段早已发生破坏。然而，4.3节和4.4节的相关计算证明灌浆连接段的总损伤值仅在2‰之内，由此证明规范[20]中方法的保守性，按此规范进行灌浆连接段的疲劳设计可能会造成不必要的浪费。

5 结 语

灌浆连接段的疲劳性能对于海上风机单桩支撑结构至关重要。基于385种工况下的广东某实际5 MW单桩风机支撑结构在风、浪荷载作用下的动力响应分析，获取了灌浆连接段荷载边界条件时程。建立灌浆连接段精细化有限元子模型，将荷载边界条件转化为应力时程。由此对风、浪荷载作用下的灌浆连接段进行了疲劳性能评价，得到了如下结论：

1) 对焊接剪力键焊趾附近应力分量时程进行“热点应力”法相关计算，得到在假定的海上风机20年的使用寿命中，损伤最大的剪力键的总损伤D为1.349 8×10-10。

2) 对剪力键附近灌浆材料的第三主应力时程进行相关计算，得到在假定的海上风机20年的使用寿命中，损伤最大的剪力键附近的灌浆材料总损伤D为1.54×10-3。由此可见，灌浆连接段的疲劳性能由灌浆材料控制。由于损伤值远小于限值1/3，也说明在现有的荷载条件下，灌浆连接段在20年的使用寿命中不会发生破坏。

3) 分析产生损伤较大的前几种工况进行可知，风速为12 m/s时，最接近5 MW标准风机的额定风速，此时风机运行对单桩结构的推力最大，产生的疲劳损伤也最大；同时海浪谱的峰值频率与结构基频越接近并不会对灌浆连接段产生越大的损伤值。

4) 采用DNVGL-ST-0126规范[20]的相关方法，对灌浆连接段整体疲劳性能进行了评价。经过相关程序计算，发现产生损伤值较大的前9种工况的Di都远大于1，总损伤值D更是达到38.62；与1)和2)条结果比较，说明了规范[20]的整体疲劳性能评价方法的过分保守性。

文中所提出的对于风、浪荷载作用下的单桩基础灌浆连接段的疲劳性能评价方法是具有较好地普适性的，可以推广到其他结构形式中的灌浆连接段中。然而，计算中目前仅有一年的实际场地风、浪实测数据，用该数据推测海上风机单桩支撑结构灌浆连接段的疲劳性能可能不具有代表性，未来的工作中应采用更加丰富而全面的数据进行分析。