在建导管架平台圆管风致涡激振动及减振研究

刘利琴，陈益群，沈文君，李 昊，吴志强

(1. 天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2. 交通运输部天津水运工程科学研究所 工程泥沙交通行业重点实验室，天津 300456；3. 天津大学 机械工程学院，天津 300072)

随着对海洋资源的开采逐渐向深海转移，导管架平台的作业水深也在不断增加。大型导管架平台通常采用卧式建造的方法，由于安装顺序的不同，会出现单边约束的圆管(如图1所示)[1]，建造过程中圆管会受到风载荷而引起结构振动，影响较大的包括抖振和涡激振动[2]。其中涡激振动是一种由于流体流经物体表面，产生旋涡脱落，当旋涡脱落频率恰好接近结构自身频率时产生的自激式振动。涡激振动往往在低流速时发生，引起圆管振动，使得结构的疲劳寿命降低。因此研究导管架建造过程的风致涡激振动问题，并提出减小振动的措施，对保证导管架平台的结构强度和疲劳寿命有重要意义。

图1 导管架建造过程模拟图Fig. 1 Simulation diagram of jacket construction process

近些年来，有学者对导管架平台涡激振动展开了研究。汪睿[2]基于DNV规范和疲劳简化分析方法对导管架风致涡激振动引发的圆管疲劳进行分析，同时采用“狗骨头”型防震锤进行减振分析。秦晶[3]使用CFD的方法，建立三维圆管模型与防震锤模型进行数值仿真，结果说明防震锤可以有效减小三维圆管模型的升力系数。

在减振分析方面，众多学者将研究方向投到了非线性能量阱(nonlinear energy sink，简称NES)上，因为其减振频带宽，适用于不同的激励条件下，成为研究的热点[4]。NES是一种被动减振技术，其由较小的质量、非线性刚度和阻尼元件组成，将主系统中的能量转移到NES中，通过阻尼元件耗散从而实现主系统的减振效果。Georgiades和Vakakis[5]将NES应用到线性梁的减振研究中，在脉冲激励下NES表现出能量单向传递的特性，耗散的能量高达87%，具有出色的减振效应。Ahmadabadi和Khadem[6]考虑了在悬臂梁中加入NES进行减振分析，采用接地和不接地的连接方式来针对冲击载荷作用下的悬臂梁进行研究，并通过数值分析参数优化，实现89%的能量耗散。Zhou等[7]通过在有内部流体的悬臂梁管道上附加非线性能量阱，分析了结构的分岔特性，考虑了不同布置位置和NES参数进行了减振研究。Blanchard等[8-9]在层流中产生涡激振动的圆柱中附加NES，分析其非线性力学特性。还有学者运用能量转移后的非线性能量阱的剧烈振动进行发电研究[10]。

为了减小风致涡激振动对导管架的破坏，把出现单边约束的导管架圆管处理成悬臂梁，研究其风致涡激振动，将NES作为减振器，并结合粒子群优化算法对减振器结构参数进行优化，实现了给定参数范围内的最优减振效果，为将NES应用到导管架风致涡激振动减振提供参考。

1 导管架圆管建模与求解

1.1 运动方程的建立

将单边约束圆管考虑成悬臂梁的形式，NES布置在结构外部，如图2所示。基于欧拉伯努利梁理论，利用van der Pol尾流振子模型模拟圆管受到的流体力[11]，不考虑梁的轴向伸长，建立结构附加NES的运动方程如式(1)所示：

图2 单边约束圆管模型Fig. 2 Unilateral constrained circular pipe model

(1)

其中，w为横向位移；u为NES的位移；x为悬臂梁轴向位置；L为梁的长度；d为NES到梁固定端的长度；EI为结构的抗弯刚度；c为梁阻尼；m0为梁单位长度质量；mnes、cnes、knes分别为NES的质量、阻尼和非线性刚度；δ(x-d)为狄拉克函数；q=2CL/CL0，CL为振动圆柱体的升力系数，CL0固定圆柱体的升力系数；wf=2πStU/D为旋涡脱落的频率，St为斯托劳尔数；λ和A是试验确定的参数，λ表示非线性项中的小参数，A是圆管和流体之间的耦合动力参数；D为圆管截面直径。

尾流振子模拟风对导管架圆管的作用力表示为

(2)

式中：ρ为流体密度；CD为阻力系数，不同雷诺数下的阻力系数不同；U为定常风速。在大气层边界内的定常风速U沿高度z方向的呈指数关系变化，可写成下式：

(3)

其中，α取0.12；U10为10米高处风速。

为将运动方程(1)无量纲化，给出以下无量纲参数：

为了表示方便，去掉符号上标“～”，得到方程(1)对应的无量纲化方程：

(4)

1.2 伽辽金法离散

基于伽辽金方法来求解运动方程，使用振型函数和模态坐标来表示几何位移：

(5)

其中，φi(x)表示i阶振型函数。悬臂梁的振型函数可以表示为：

可悲的是，当一个人如日中天的时候，谁会去想居安思危？“安”的时候不会想到“危”，“安”的时候也不相信有“危”。三十年河东三十年河西，就是对不懂得居安思危的人的惩罚。

(6)

其中，x为无量纲后的长度，范围在[0,1]；βi通过求解方程cos(βi)cosh(βi)=-1来确定，β1=1.875，β2=4.694；pi(t)和ri(t)分别表示梁结构和尾流振子模型的模态广义坐标。将式(5)代入式(4)中，方程两边都乘以φj(x)，并从[0,1]进行积分，利用振型的正交性，可以得到方程：

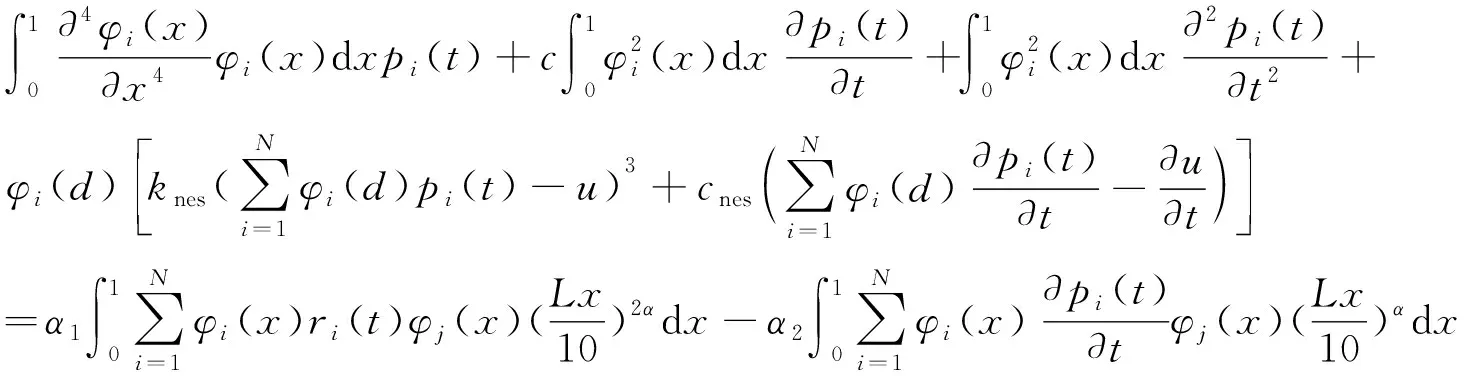
(7)

(8)

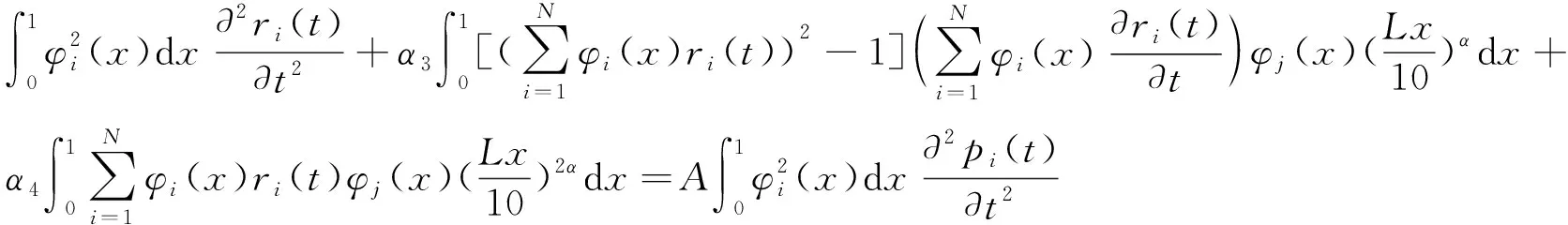
(9)

在计算的时候选取约化风速在0～20之间，主要引起此圆管前两阶频率的涡激振动，没有激发高阶的模态，因此N取为2可以满足精度要求。通过二阶离散，采用四阶龙格库塔方法对离散之后的方程组(7)、(8)、(9)进行数值求解。

2 NES减振数值模拟

计算采用的圆管参数[2]为D=0.762 m,m0=401.5 kg/m,E=2.1×1011Pa,L=31 m,I=0.003 5 m4。该圆管的无量纲结构阻尼c1=0.01，c2=0.065，前两阶固有频率分别为f1=0.784 Hz，f2=4.95 Hz。参数λ、A根据Facchinetti[12]的建议取值λ=0.3，A=12；当计算风速的雷诺数处于亚临界区间时，St=0.2，CD=1.2；当计算风速的雷诺数超过亚临界区间时，考虑圆管表面光滑，St和CD根据Günter Schewe的实验[13]取值。空气密度ρ=1.225 kg/m3，为了表示的一般性，引入约化速度Ur=U10/(f1D)，f1表示结构的一阶固有频率。

将上述参数代入式(7)～(9)并数值求解，可以求得不同约化速度下悬臂梁自由端部的无量纲响应幅值。

首先计算不附加NES的情况，结果如图3所示。计算表明，约化速度在0～20内，圆管出现了两个涡激共振区域：第一个在Ur=4.8处，共振幅值达到0.092；第二个在Ur=12.8处，共振幅值达到0.013 3。因此，圆管在较低风速下的位移响应更大，是减振的重点，以下减振研究针对Ur=4.8进行分析。

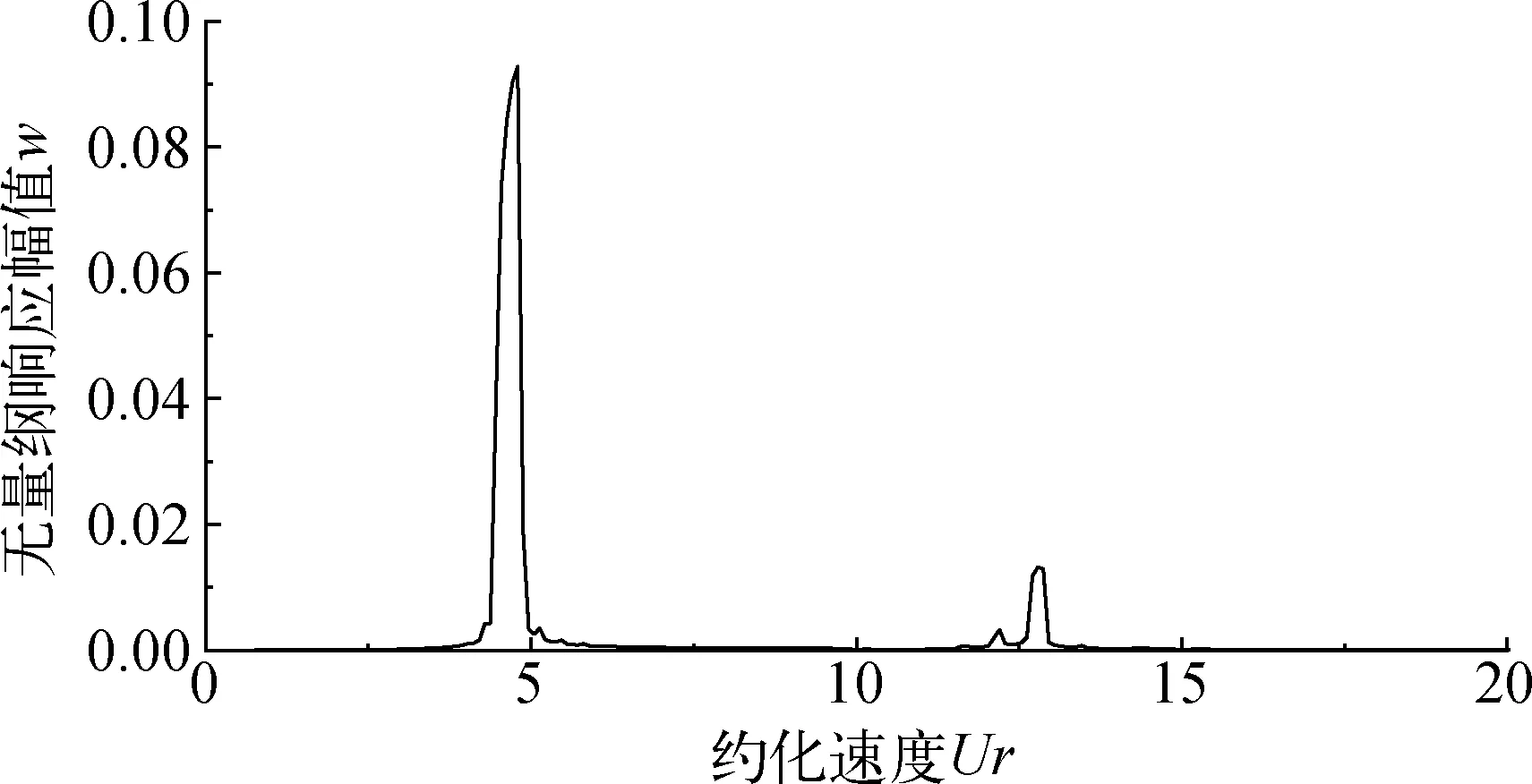
图3 不同Ur下的梁端位移幅值(不加NES)Fig. 3 Displacement amplitude of beam end under different Ur(without NES)

在梁中点增加NES，分别选取两组不同的减振器参数(ε=0.002,knes=15,cnes=0.001；ε=0.002,knes=15,cnes=0.001 5)进行计算，分析NES的减振效果。图4给出了Ur=4.8时有、无NES时的梁端位移对比。结果表明，两组不同参数的减振器均具有一定的减振效果，图4(b)的位移幅值在0.06附近，相对而言减振效果更好。

图4 不同参数NES的减振效果对比Fig. 4 Comparison of vibration reduction effects of different parameters NES

因此，不同参数的NES的减振效果不同，合理选取NES的参数对最终的减振效果有较大的影响。然而，如果人为选择计算参数并采用数值方法进行全局搜索，计算量大，效率较低。为了更加高效地获得NES的最佳减振参数组合，采用了粒子群优化算法进行NES参数优化设计，可有效提高计算效率。

3 NES参数优化

3.1 粒子群优化方法

粒子群优化算法是一种基于模拟鸟群觅食运动的随机优化算法，其优点是可以在大范围内进行参数的优化设计。在运用粒子群算法的时候把每一个个体看成一个粒子，确定目标函数，把目标函数考虑成适应度函数，每一个迭代步中每个粒子都由自己的速度来决定移动的距离和方向。最终根据计算得到的适应度值来判断粒子是否处于最优解。

使用粒子群算法进行参数优化的步骤：

1) 初始化随机种群，选择种群的大小,每个种群包含位置和速度属性，通常初始速度设定为零。

2) 计算每个粒子个体的适应度，也就是目标函数值。

3) 通过对比个体最优适应度Pbest(每个个体对应的梁端位移有效值)和种群历史最优适应度Gbest(种群对应的最优梁端位移有效值)，基于式(10)更新每个个体的位置Xj和速度Vj，与此同时，种群历史最优适应度Gbest也会不断更新。

Xj(t)=Xj(t-1)+Vj(t)

Vj(t)=θVj(t-1)+n1R1[Pbest-Xj(t-1)]+n2R2[Gbest-Xj(t-1)]

(10)

其中，θ表示惯性权重，一般取值在0.4～0.9之间，惯性权重越大，粒子全局搜索能力越强，越小局部搜索能力越强；n1、n2代表学习因子和社会因子，一般设置为2；R1、R2为[0,1]内的随机数。

4) 采用线性递减的惯性权重θ来防止粒子群优化收敛与在局部最优解，同时加快收敛的速度。

5) 判断是否达到最大迭代次数，若无则重复(2)～(4)步。

6) 输出最优参数。

整体优化过程如图5。

图5 优化过程图Fig. 5 Optimization process diagram

3.2 优化结果及分析

取目标函数为悬臂梁自由端处有效值位移的最小值，其表达式为：

Fun=min.RMS[F(knes,cnes)]

(11)

考虑导管架平台的实际情况，将NES布置在悬臂梁的中点，优化参数为NES的非线性刚度knes和阻尼cnes。在实际工程使用时不希望附加过大质量的NES，满足减振效果的前提下，应当选取最小质量比或对导管架结构强度影响最小的参数组合，这里选取了八种不同质量的NES(对应Case1-Case8共八个工况，见表1)，可根据结果进行适当选择。knes的取值范围为[0,1 000]，cnes的取值范围为[0,1]。图6给出了Case2的优化过程。可以看到，五次随机初值下的优化结果在迭代次数接近50的时候到达了相同的种群历史最优适应度，说明了粒子群优化的有效性，优化结果对初值不敏感。

表1 粒子群优化结果

图6 粒子群优化过程(Case2)Fig. 6 PSO process (Case2)

表1给出了八种不同工况下、Ur=4.8时，采用粒子群优化法迭代了100次之后得到的优化参数，及根据得到的NES参数计算得到悬臂梁自由端的位移有效值。由表1可以看出，不同的质量比对应的优化非线性刚度值和阻尼值不同；随着质量比的增大，得到的优化非线性刚度和阻尼值随之增大，目标函数值随之减小，Case8的最优RMS(F)值为0.011 6，具有较好的减振效果。

图7和图8分别给出了Case3和Case6梁自由端处的时间历程、频谱图和相图，对比了不同NES参数的减振效果。

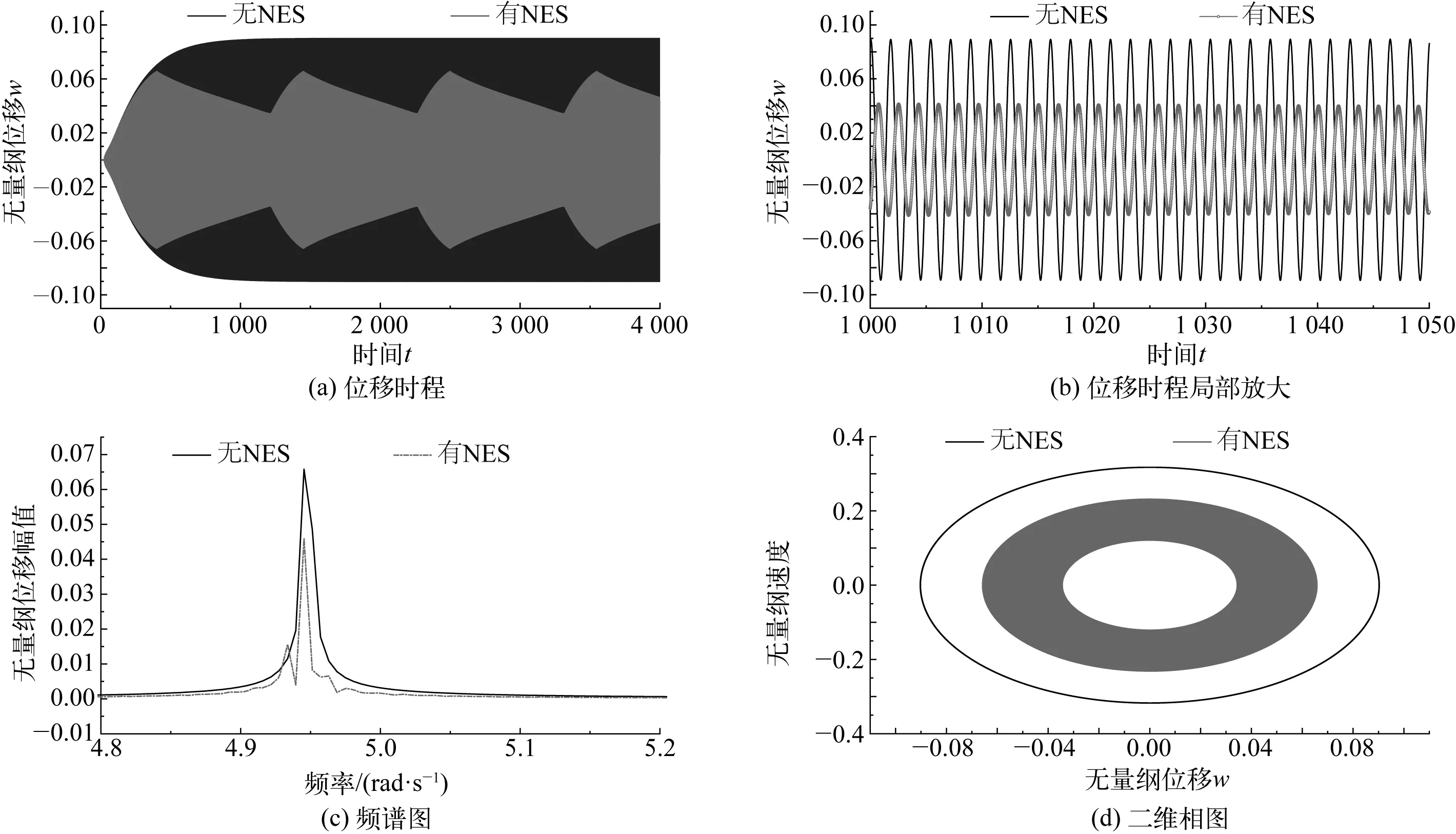
图7 减振效果对比(Case3)Fig. 7 Vibration reduction comparison (Case3)

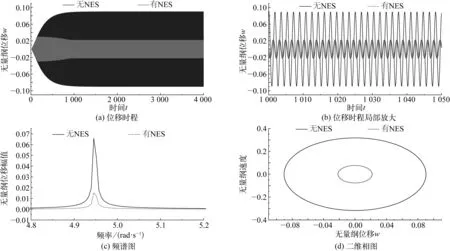
图8 减振效果对比(Case 6)Fig. 8 Vibration reduction comparison (Case6)

图7给出了Case3的减振效果。由图7可以看出，设置了NES后梁自由端的位移响应受到了一定的抑制，其位移为幅值不断变化的非简谐运动，但位移轨迹在一定范围内波动，如图7(a)和图7(d)所示；增加了NES后，梁端位移为多频率运动，但主要频率在4.94 rad/s附近，接近梁结构的一阶固有频率，如图7(c)所示。

图8给出了Case6的减振效果。由图8可以看出，梁端位移为周期运动，结构的大部分能量传递到了NES上，并通过NES进行耗散；该减振器作用下梁端位移主要呈现单一周期运动，与Case3相比，其减振效果更为明显。

4 结 语

对大型导管架平台卧式建造过程单个圆管的风致涡激振动展开研究。建立了圆管风致涡激振动力学模型，采用NES对结构进行减振，并基于粒子群优化算法对NES进行参数优化，结论如下：

1) 采用伽辽金方法离散悬臂梁运动偏微分方程，并进行数值求解，分析了圆管的风致涡激振动。结果表明Ur=4.8和Ur=12.8时，圆管发生风致涡激振动。其中Ur=4.8时，振动幅值较大，影响结构疲劳寿命，甚至导致结构损坏。

2) 在梁中部增加单个NES非线性减振器，采用被动减振方法进行减振。结果表明，采用NES减振器，可有效减小结构的风致涡激振动。不同的NES参数的减振效果也不相同，为了达到更好的减振效果，需要对NES参数进行优化设计。

3) 针对不同的NES质量，基于粒子群优化算法对NES的非线性刚度和阻尼参数进行了优化。结果表明，合理选择NES参数可以达到更好的减振效果；采用粒子群优化算法可以便捷、快速获得减振效果更优的NES最优参数组合。

本研究中没有分析NES的位置影响，在今后的工作中可进一步研究NES位置或者多个NES的布置对梁结构减振效果的影响。