运用适时点拨,提升思维品质
赵碧泉

[摘 要] 在小学数学课堂教学中,提升学生的数学思维品质是重要的教学目标,教师是学生数学学习的引导者,运用适时点拨能够有效地提升学生的思维品质。基于此背景,文章对在“重复时”点拨,突破思维僵局;在“困惑时”点拨,引发思维顿悟;在“生长处”点拨,引导思维概括;在“错误处”点拨,深化数学理解的策略进行了探究。
[关键词] 小学数学;教学;适时点拨;思维品质
在小学数学教学实践中引入“慢艺术”,可以聚焦学生的情感体验,特别是针对新知的教学过程或者是具有创造性的教学环节中,逐渐放缓的教学节奏,能够使学生全身心地投入其中,并且展开主动思考,顺利突破教学重点和难点。教师在学生学习数学的过程中,进行适时点拨,能够有效地提升学生的思维品质。
一、在“重复时”点拨,突破思维僵局
教师在课堂教学过程中要抛出具有开放性的问题,要让学生立足于不同的方法展开解答,目的是为了更好地培养学生的发散性思维,但是很多学生却在一条道上走到黑。此时就需要教师把握恰当的时间,对学生进行点拨和启发,确保课堂资源的正向生成。
例如,在教学“两步计算应用题”时,我首先为学生创设了真实的情境:为了表扬班级内学生的积极表现,老师购买了40支笔,并打算分给8个不同的小组,每个小组能够分到几支?在这一问题情境创设之后,我要求学生对其中的条件进行改变,将其转化成为一个需要经过两步计算的应用题。
师:如果我们所购买的笔的支数是不知道的,可以如何设计问题?
生1:可以说买了5盒笔,每盒笔有8支。
师:回答得非常好!大家还有不同的提问方法吗?
生2:老师购买了4盒笔,每盒有10支。
师:还有吗?
接下来学生所提出的是每盒20支、一共购买2盒的方法,很显然这样下去,不管是思考还是回答都毫无意义,于是我及时对学生进行点拨:刚才大家使用了怎样的方法将40支笔进行了转换?
学生回答是根据乘法。于是我继续追问:是否还可以选择其他的计算方法呢?
经过我的进一步引导和启发,学生展开了新的思考,实现了新的生成。
上述教学案例中,学生饱含热情地探讨,但是却因为生1的思维受到了强烈的暗示,产生了定式,所以具体的回答仍停留在原地,难以取得突破,此时便是教师给予点拨和启发的最佳契机,带领学生突破思维的禁锢,为学生提供更广阔的思考空间,使其思维往纵深拓展。
二、在“困惑时”点拨,引发思维顿悟
数学学习过程中不可缺少教师的有效介入,如果仅依靠学生自主展开单纯的研习,很有可能偏离原有的方向,也容易被其他因素所干扰,因此教师需要在具体的学习过程中及时审视学生的学习状态,准确把握学生的困惑处、混沌处以及存在争议之处,并及时给予援助和启发,这样学生的思考及学习才能具备正确的方向。
例如,一位教师在教学“最简分数”一课时,有这样一个教学片段。
生1:我认为最简分数就是分子和分母都有公因数1。
师:大家认为他的回答对吗?是否可以举例说明?
生2:在 和 中,分子和分母都含有公因数1,但是它们却都不是最简分数。
生3:所以我们应当强调的是“只有”,公因数只有1的情况才是最简分数。
师:大家再次反复品味这句话,是否有其他不同的感受?
生4:我认为他表达得不够完整,漏掉了“分数”二字。……
……
上述教学片段中,教师的点拨十分简单,但是却能够对学生形成积极有效的引导,使学生聚焦同伴的发言,真正体会最简分数的真义。这样的引领能够明确学习的方向性,利于就此生发辨析以及思考等一系列思维活动,同时也能够聚焦学生的数学表达,提升表达的规范性。在这一教学过程中,学生有了对概念的个性化理解,建立了严谨的数学思维。
三、在“生长处”点拨,引导思维概括
实际教学过程中,教师应准确把握知识的生长点,引导学生借助数学语言进行表达,可有效帮助学生理清知识的脉絡,确保思路的清晰,同时也能够完成对数学的概括。
例如,在教学“表面积的变化”时,可以先出示例题:我使用两个棱长都为一厘米的小正方体将其拼接成为一个长方体,如何计算这个长方体的表面积和体积?并将其与之前的小正方体展开对比。
师:通过刚才的对比,你从中发现了哪些问题?
生1:长方体的体积是两个小正方体体积之和,但是长方体的表面积为10平方厘米,而两个小正方体的表面积是12平方厘米。
生2:表面积好像缩小了。可是为什么呢?
师:是呀,这究竟是为什么呢?大家能够从中发现原因吗?是否存在规律?
生3:我们可以再使用一个小正方体,将三个小正方体拼接成长方体,然后对比其表面积和体积。
师:这个想法不错,大家可以试一试。
生3:拼接之后的长方体和三个小正方体的体积之和完全相等,但是表面积仍在缩小。
生4:我们在对比时发现,如果是两个小正方体进行拼接,它的表面积减少2平方厘米,但是使用三个小正方体进行拼接的过程中,表面积少了4平方厘米。
生5:在拼接两个小正方体的过程中,有两个面是重合的,但是在拼接三个小正方体时,有四个面重合在一起。
师:这一点总结得非常好,那么我们接下来拼接六个小正方体。首先看一看这六个正方体可以拼接成几种不同的长方体?然后,进行对比,看一看哪种表面积最小并说明其原因。
学生们经过自主操作提炼出两种不同的方法:其一减少了十个面,其二减少了十四个面。很显然第二种方式的表面积更小一些。
师:那么接下来我们继续讨论导致表面积减少的原因是什么。
学生根据所拼接的实物,展开全方位的观察和分析,并思考其中的原理。
生6:因为在实际拼接的过程中存在面的重合,只要数一数重合面的数量就能够知道表面积减少的部分。
生7:当两个小正方体进行拼接时,减少的只有两个面,使用三个小正方体是减少了四个面……
生8:根据这个规律可以发现,每次拼接都会出现面的重合,而且重合的面减少两个。
上述教学案例中,教师准确把握了知识的生长点,并组织学生自主拼一拼、说一说,使学生可以立足于实践完成对规律的梳理和总结,既有效地锻炼了学生的动手操作能力及分析能力,还有助于培养学生的数学概括能力。
四、在“错误处”点拨,深化数学理解
小学生在数学学习的过程中,会经常出现学习错误,对于课堂上学生出现的学习错误,教师不能够进行简单规避,而应该在他们的数学学习“错误处”进行点拨,以此促进他们的数学理解,让学生经历纠错、改错的过程,从而达到高效化教学的目的。
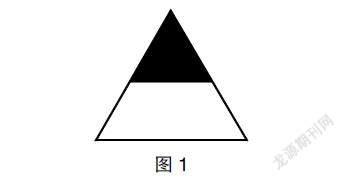
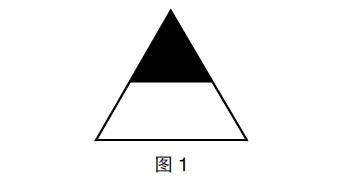
师:同学们,下面这个图形中的涂色部分用“ ”表示对吗?

生:不对。因为没有平均分成2份。
师:那么这个图形中的涂色部分能不能用分数表示呢?
生1:不能。
生2:是的。因为没有平均分,肯定是不能用分数表示的。
师:如果我在这个图形上加两条线,你们看看还能不能用分数表示?

生3:可以的。可以用“ ”表示。
师:现在怎么又可以了呢?
生3:因为这样看是把这个三角形平均分成了4份,涂色部分占了一份。
生4:看来我们碰到这一类图形时,还要仔细思考是不是真的没有平均分。
生5:其实,很多图形从表面上看没有平均分,实际上是平均分的。因此,我们不能够简单地从表面上看能不能用分数表示。
以上案例中,对于学生片面化的理解而导致的错误教师大胆地展示出来,并且,通过给三角形添加辅助线的方式让学生明白一个图形是不是平均分不能看表面,而应该进行仔细观察,深入思考。只要找到平均分成了几份,就能够用分数表示。这样,学生对分數的本质意义的理解也就更加深刻了。在这个过程中,学生有效地把握了数学学习方法。
总之,在发展数学知识以及能力的过程中,需要经历一个缓慢的递进过程,需要教师立足于教学实践,为学生营造有利于其展开思考和体会的良好氛围,而且应当将慢艺术灵活地运用其中,只有这样,学生才能够和数学知识之间展开深度高效的对话,才能有效梳理知识脉络,高效习得知识。

