基于近场声全息的聚焦换能器声场测量方法研究
刘海楠,赵 鹏,叶晓同,王月兵
(中国计量大学 计量测试工程学院,浙江 杭州 310018)
1 引 言
高强度聚焦超声(high intensity focused ultrasound, HIFU)设备在医疗设备中占有很大的比重,HIFU设备通常要求工作频率在500 kHz以上,并且在工作时使聚焦区域肿瘤组织的温度上升到65 ℃或以上[1],这就需要准确的测出HIFU设备焦域的范围与声压的大小,防止损害正常组织。目前对换能器的声压分布测量使用最为广泛的是水听器法,但HIFU设备焦点处声压较大,直接测量焦点面易造成水听器损坏[2]。近场测量法[3]为解决这一问题提供了1种可行的技术手段,通过测量非焦点区域的声压较小的平面推算出焦点平面的声压。近场测量法是声全息技术领域的一个部分,该方法最早由Williams和Maynard[4]在经典声全息的基础上提出,之后近场声全息的应用方面越来越广。
袁文俊[5]等根据亥姆霍兹公式推导了由近场测量数据推算远场声压的公式,并通过对线列换能器的实测说明了测量近场声压推算远场声压的可行性。熊久鹏[6]等提出了二维平面声压构建技术,利用2条相互垂直的轴线声压实现了对矩形活塞换能器的声场重建。文献[5,6]提出的方法完成了对平面活塞换能器、圆柱形换能器的近场推算。靳建嘉等[7]利用积分法对低频换能器进行远场推算;王成等[8]提出基于近场测量法的水声换能器声场重建方法,利于水听器在焦点平面前进行扫描,得到测量面的复声压,通过等效声源叠加和积分变换实现对声场的重建。积分法虽然能够有效推算成焦点面的声压分布,但是在推算时会花费大量时间,严重影响测量效率。
本文基于空间傅里叶变换[9]的近场声全息技术,提出一种针对聚焦换能器的高测量效率的声场测量方法。以球面自聚焦换能器[10]为实例,进行仿真研究与实验测量,从理论和实验两方面验证测量方法的精度与速率。
2 基本理论
2.1 球面自聚焦换能器声压分布推算原理
根据基尔霍夫衍射积分,导出球面曲率半径为R,均匀辐射的球面自聚焦换能器在线性声场下单频波声场中任意点(r0,θ)的声压表达式(也称作瑞利积分)为[11]:
(1)
式中:k=2 π f/c为波数; f为超声频率;c为媒质中的声速;p0=jρfu0,ρ为媒质密度,u0为振动速度;b为坐标原点到换能器边沿的距离;R1为坐标原点到面元ds的距离;r为面元到Q(x,y,z)的矢径:
(2)
式中:φ为面元ds与Q的方位角之差。其它几何参数如图1所示。
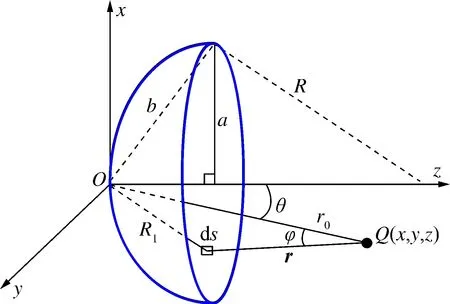
图1 球面自聚焦换能器的几何参数及计算坐标Fig.1 Geometric parameters and calculated coordinates of spherical self-focusing transducer
2.2 基于近场声全息的重构面推算原理
均匀理想流体介质中的小振幅声波的波动方程为:
(3)
对波动方程进行Fourier变换,得到不依赖于时间变量的Helmholtz方程:
2P(r)+k2p(r)=0
(4)
式中:k=ω/c为波数,ω=2 π f为角频率。
定义全息面(测量面)用H表示,重构面(源面)用S表示。
在平面z=zs的Dirichlet边界条件下,对于zH>zs的空间为自由场的情况,式(4)的解为:
p(xH,yH,zH)=∬SPD(xS,yS,zS)×gD(xH-
xS,yH-yS,zH-zS)dxSdyS
(5)
式中:∬S表示积分在无穷大的平面S上进行;PD为Diirchlet边界条件下声压;gD为Dirichlet边界条件下无穷大平面的Green函数:
(6)
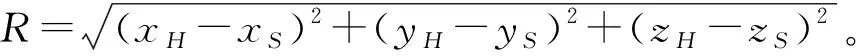
对式(5)两边取空间Fourier变换,将空域卷积化为波数域中角谱的乘积:
P(kx,ky,zH)=PD(kx,ky,zS)GD(kx,ky,zH-zS)
(7)
式中:P(kx,ky,zH)为声压p(xH,yH,zH)的空间Fourier变换;PD(kx,ky,zS)为边界条件PD(xS,yS,zS)的Fourier变换;GD(kx,ky,zH-zS)为Green函数的空间Fourier变换,解析表达式为:
GD(kx,ky,zH-zS)=ejkz(zH-zS)
(8)
对式(7)两边取傅里叶逆变换可得H面声压:
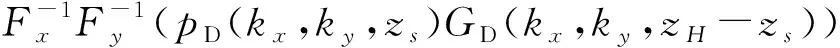
(9)
以重建误差作为衡量重建效果的标准,本文所用重建误差的计算公式与文献[12]一致,计算公式为[12]:
(10)

根据本文提出的推算步骤如图2所示。
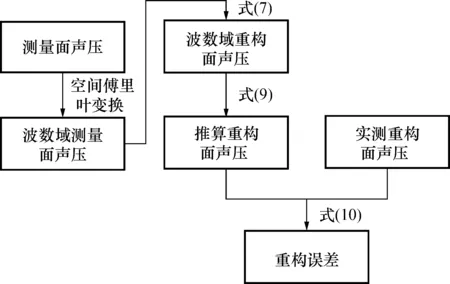
图2 声场推算流程图Fig.2 Sound field estimation flowchart
3 仿真研究
仿真模型如图3所示,设置球面自聚焦换能器的焦距F=140 mm,直径为d=22 mm,谐振频率f=2.5 MHz。重构面为焦点处20 mm×20 mm的截面,测量面选取为焦点面前10 mm处的20 mm×20 mm的截面。将20 mm×20 mm大小的测量面离散成500×500的采样点,每2个相邻采样点间隔为 0.04 mm,水中声速为1 480 m/s,密度为1 000 kg/m3。
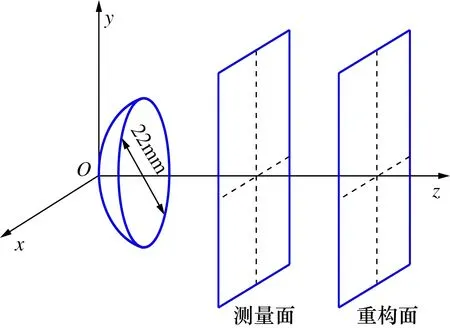
图3 聚焦换能器仿真模型Fig.3 Focused transducer simulation model
在进行仿真时,将球面声源离散成无限多个小面元,每一个小面元都看作为一个点源,看作点源的条件是点源半径r比声波波长λ小很多,本文取点源半径为λ/5,然后利用瑞利积分计算每个点源产生的声压,最后将所有这些点源辐射的声波叠加起来,就可得到整个的辐射声压。基于此仿真得到仿真测量面和仿真重构面的声压,如图4和图5所示。
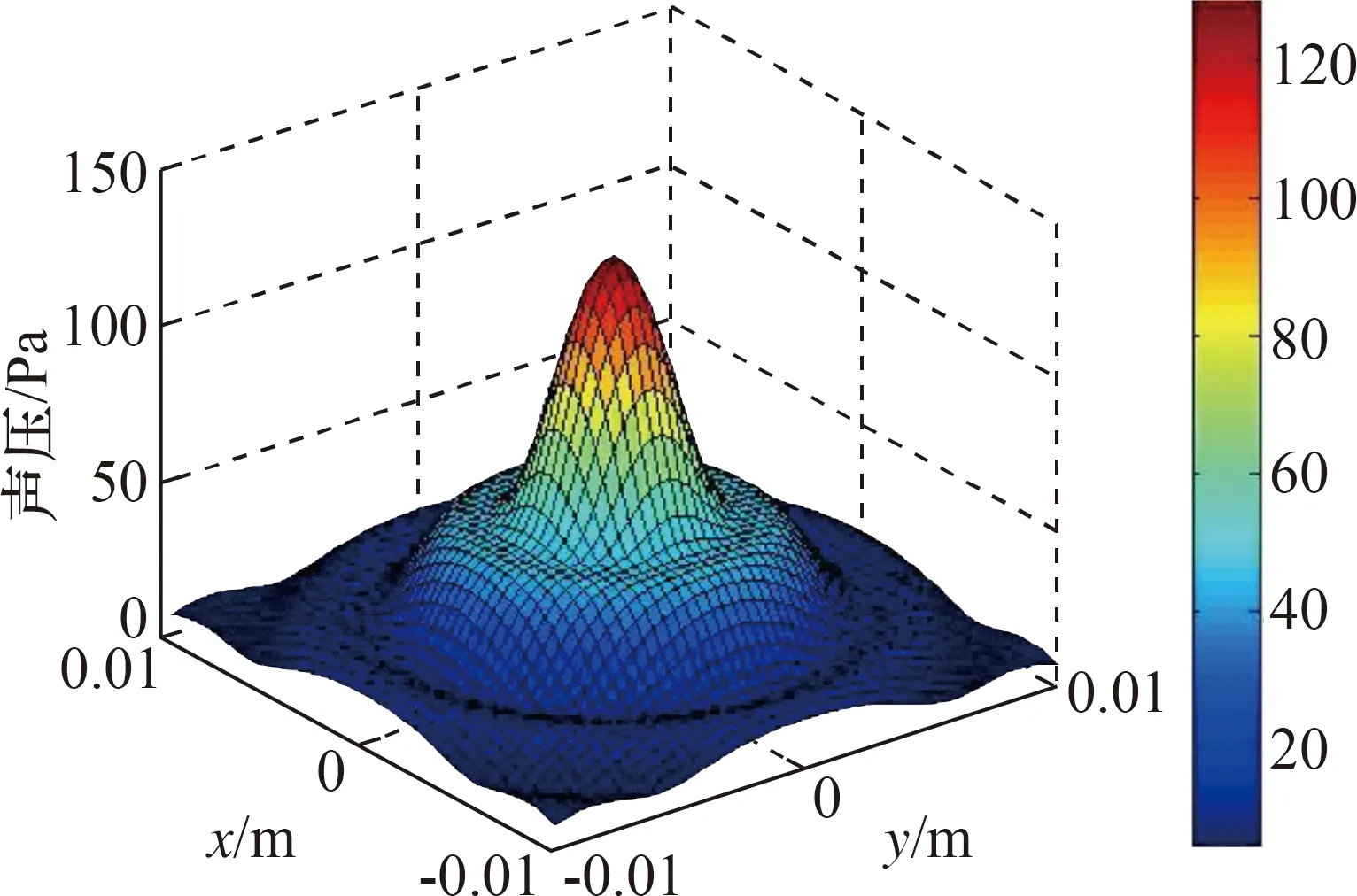
图4 仿真测量面声压分布Fig.4 Simulation measurement of surface sound pressure distribution
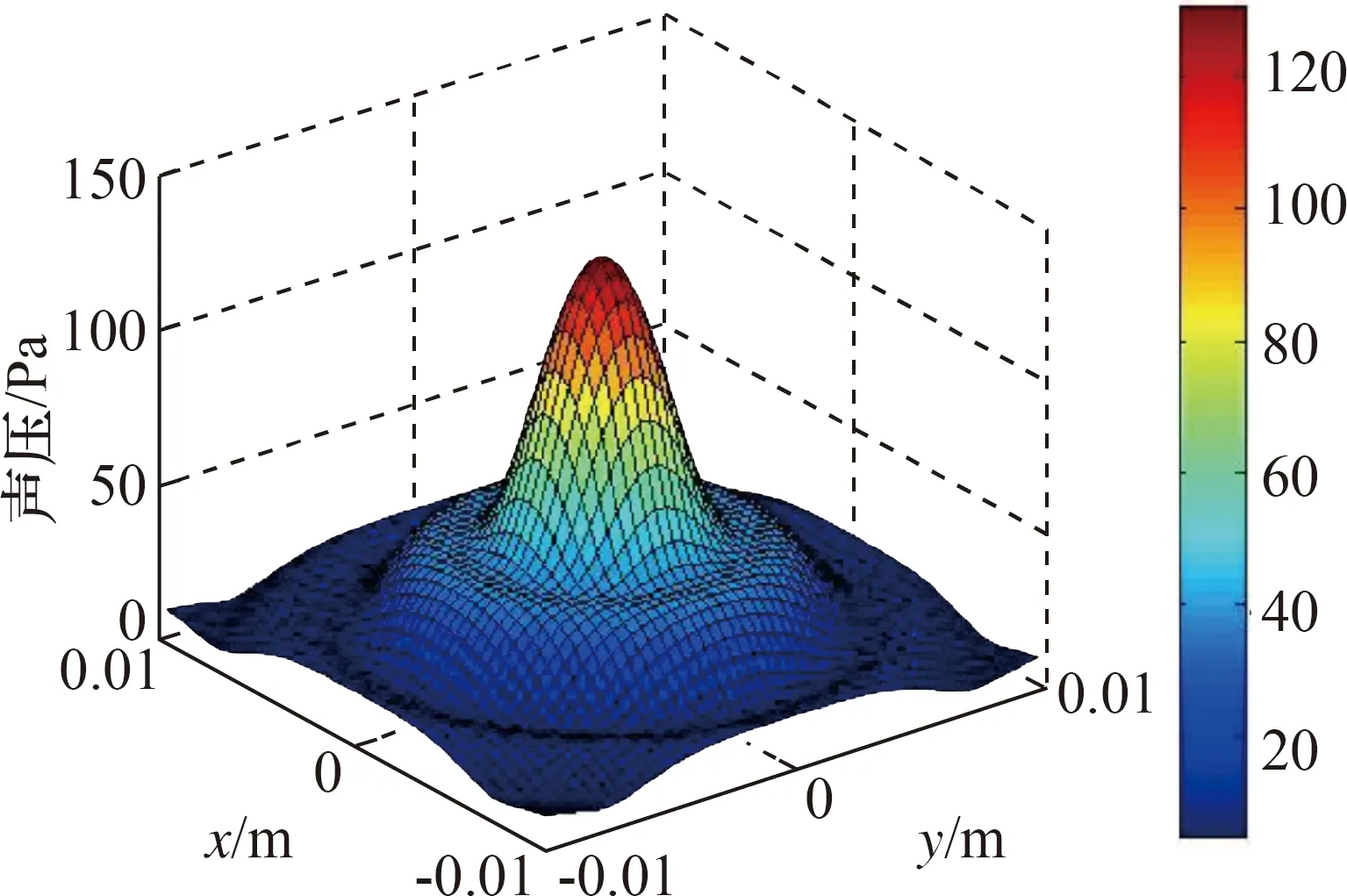
图5 仿真重构面声压分布Fig.5 Simulation reconstruction surface sound pressure distribution
根据仿真得到的测量面的声压值,利用式(9)推算理论重构面声压,得到如图6所示。
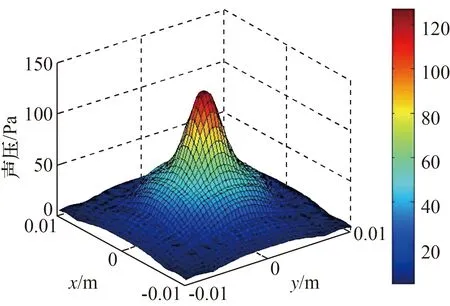
图6 推算重构面声压分布Fig.6 Calculate the reconstructed surface sound pressure distribution
将仿真重构面声压值作为真实值,与推算得到的声压值利用式(10)进行误差计算,可得误差为4.06%,在声学计量要求的误差范围10%内[8],因此基于空间傅里叶变换的近场声全息技术可有效应用于聚焦换能器的声场重构。在实验室工控机上,保持相同的工作环境条件下使用MATLAB软件分别运行本文方法和文献[7]所述的算法,比较结果如表1所示。工控机配为Intel Core i7 4790CPU,512G Bits固态硬盘,16G Bits运存。

表1 方法比较Tab.1 Method comparison
由表1可知,相比于文献[7]中的积分法,本文采用的空间傅里叶变换法在推算效率上提高了一倍。通过计算,在测量点数相同的条件下,本文以及文献[7]在对聚换能器的声场推算误差均在10%以内,2种方法均符合声学计量要求。根据式(10)计算的是平面各点的平均误差,结果与所选平面大小直接相关,尤其声场分布的边缘部分信噪比低,容易使推算值和误差值有很大的相对误差,因此一般选取测量面大小为声源区域边长的1.5倍或2倍,本方法应用对象是聚焦换能器,声波较为集中,可适当减小测量面积。
4 实验研究
4.1 实验系统
实验系统如图7所示,硬件系统主要包括信号源、球面自聚焦换能器、水听器、运动控制机构、前置放大器、数字示波器、计算机等。信号源发射频率为2.5 MHz,幅值(峰峰值)为20 V的正弦脉冲信号,激励聚焦换换器,将同步信号接入示波器作为触发信号。探针水听器固定在三维行走机构上,接收到的信号经前置放大器后被示波器读取,读取到的数据经串口由计算机保存处理。
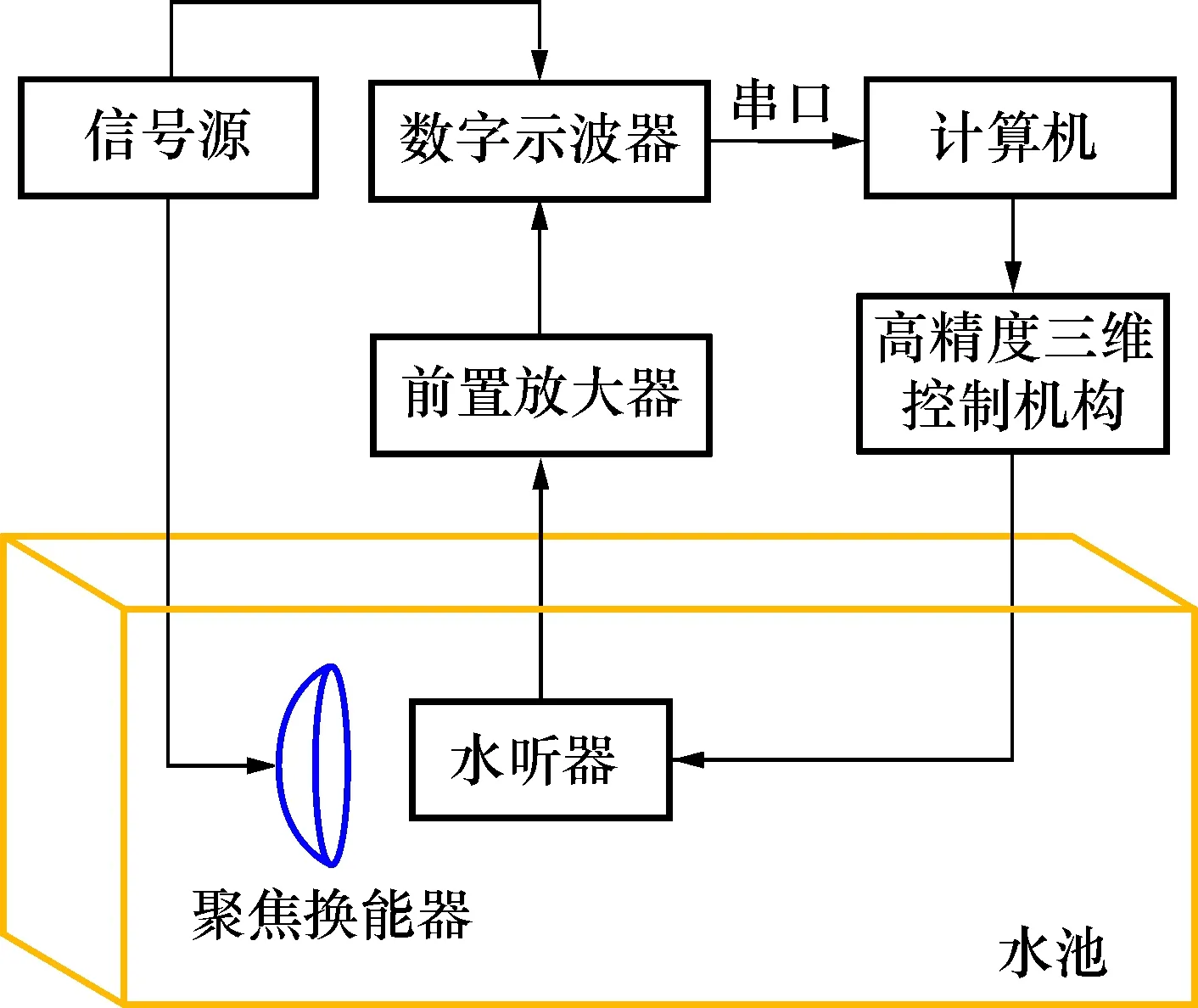
图7 测量系统示意图Fig.7 Measuring system diagram
4.2 实验结果分析
实验选用的聚焦换能器与仿真时设置的一致,测量面和重构面的位置与仿真假设一致。测量面相邻2点间隔为0.4 mm,在20 mm×20 mm的测量面上一共测量2 500个点,重构面位于焦点处,面积大小与测量面相等。绘制声压分布图时3个面各点均比上3个面中测量的最大声压值,以便比较。
实际测量得到聚焦换能器测量面声压分布,测量结果如图8所示。
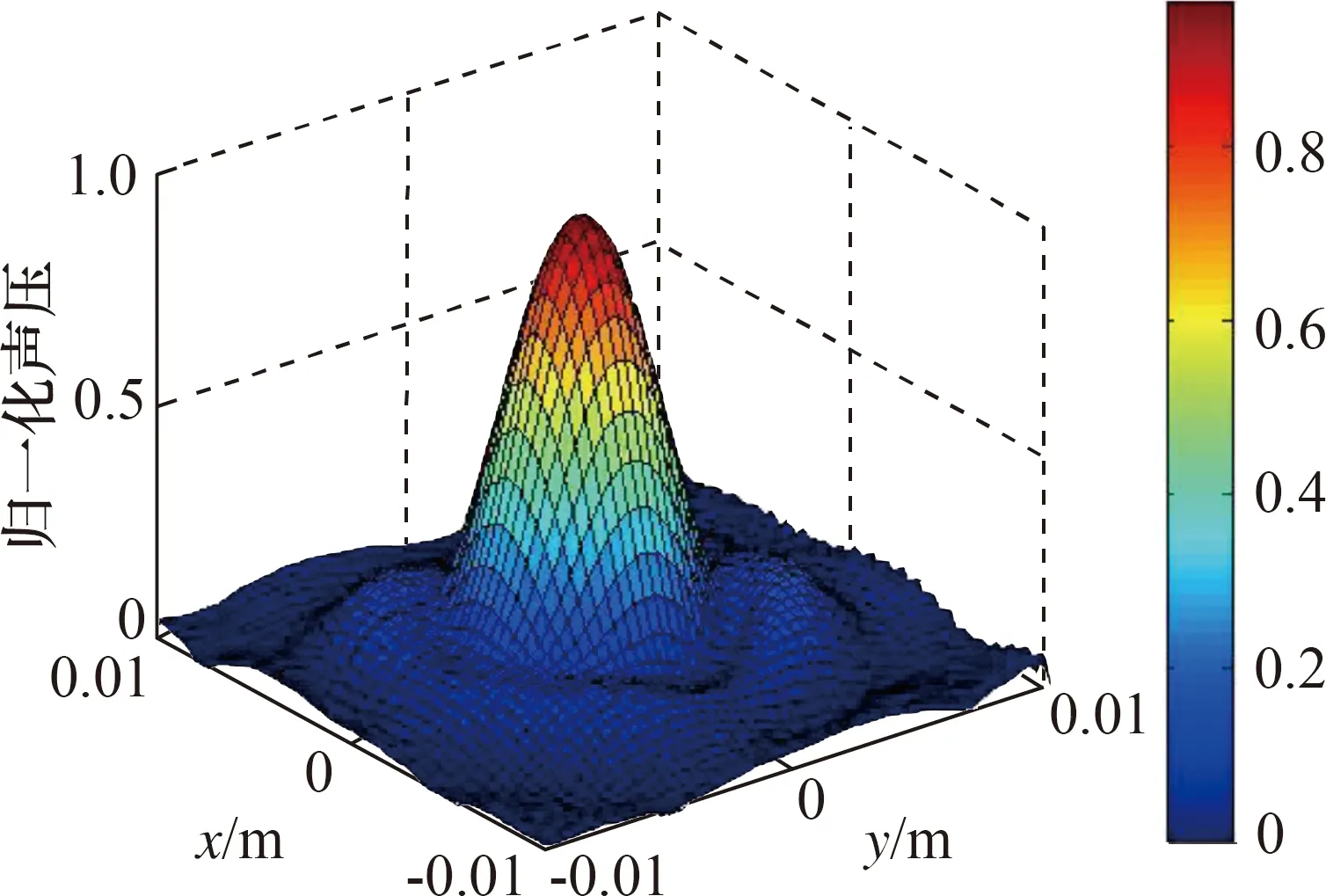
图8 测量面声压分布Fig.8 Measuring surface sound pressure distribution
调整水听器位置,得到焦点面声压分布,并将其作为真实值,焦点面声压测量结果如图9所示。
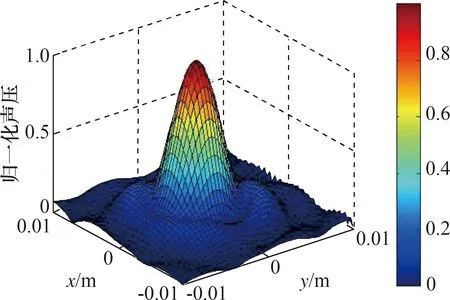
图9 焦点面声压分布Fig.9 Focal surface sound pressure distribution
利用式(9)对测量面的声压进行推算,得到重构面的推算声压,测量结果如图10所示。
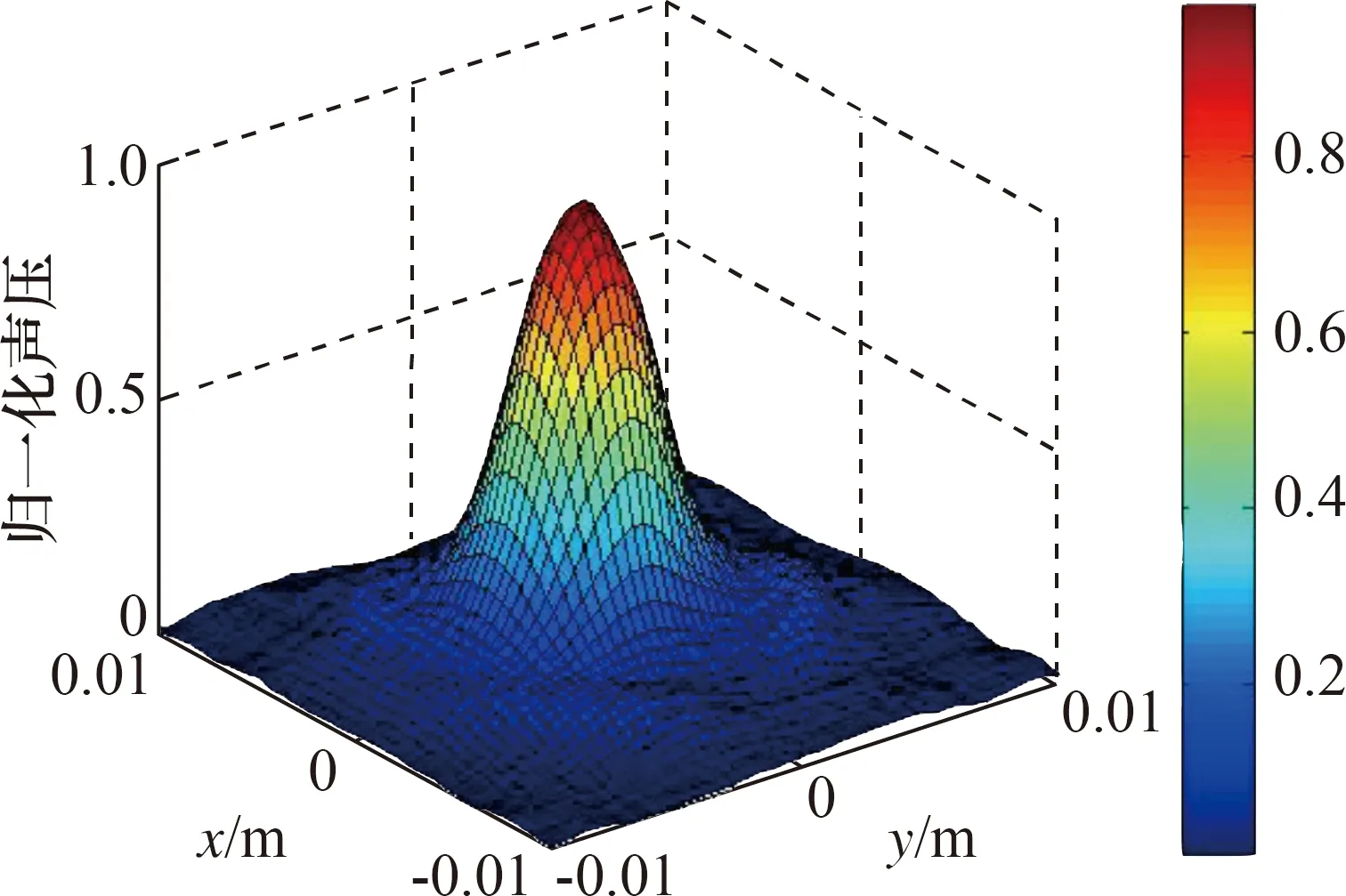
图10 重构面推算声压分布Fig.10 Reconstructing surface to estimate sound pressure distribution
通过图9和图10比较可知,推算结果与实际测量结果基本一致,将两者数据代入式(10)计算可得实验误差为5.8%,略高于仿真结果,同文献[7]相比,实验数据推算效率提高了一倍以上。分析实验误差来源,主要有以下几点:
1) 实验所处的环境不是真正的自由声场,声波的壁面反射、水面反射等都对会对信号造成一定的干扰;
2) 测量点数无法达到仿真设定的那么多,致使扫描点相邻2点间距过大,不能包含所有的声场信息,引起信息泄露,就是有限孔径误差;
3) 快速傅里叶变换的引入在加快推算速度的同时也给系统引入了卷绕误差。
5 结 论
本文利用空间傅里叶变换的近场声全息技术,提出一种高推算效率的声场测量方法。该方法通过对测量面进行声场测量,并对聚焦面进行推算重构。以球面自聚焦换能器为对象,通过仿真研究了本文提出的聚焦面声场推算方法,并通过实验测量进行了验证。结果表明,本文的推算方法,相比于文献[7]所述方法,提高了声场推算效率,同时保证了测量精度,为高强度聚焦换能器的声场测量提供了一种可行的方法。

