基于形态重建和反向跟踪的粗集料级配视觉检测
陈泽琦,范伟军,郭 斌,江文松
(1. 中国计量大学,浙江 杭州 310018;2. 杭州沃镭智能科技股份有限公司,浙江 杭州 310018)
1 引 言
粗集料是沥青混合料的重要组成材料。在建筑工程中,级配不合格的集料会影响沥青混凝土的强度,危害建筑质量[1]。目前工程中,通常采用振动筛分法对集料进行级配检测[2],该方法在筛分过程中容易堵塞筛孔,影响筛分结果,降低筛分效率。随着机器视觉技术的快速发展,图像处理技术在土木工程中的应用越来越广泛[3]。2007年,汪海年等[4]研制了粗集料形态研究系统,采用图像处理技术对平铺的静态集料进行级配分析。2013年,Prudêncio等[5]提出了一种简化的数字图像处理方法,用于分析集料的形状。2014年,史源[6]对平铺的静态集料颗粒进行背光拍摄,使用LabVIEW开发了一套集料颗粒形态特征提取系统。2017年,罗曼等[7]对不同运动状态下的集料进行研究,并对比不同的光源安装方式,总结得到了较优的集料拍摄方法。对静态集料进行视觉级配分析,需要提前将集料平铺于视场中,且每次检测的集料数量有限,导致检测效率低下,无法适应工程检测需求。而对下料过程中的动态集料进行在线级配检测,能够提高效率,满足工程检测需求。在动态集料的图像中,图像上下边缘存在不完整的集料颗粒,且每个集料颗粒会重复出现在连续的图像中,影响集料数据统计。针对此问题,陈思嘉[8]和杨建红等[9~10]采用周长面积之比判断集料颗粒是否完整,并提出轮廓匹配方法对重复出现的颗粒进行识别。利用周长面积之比判断集料颗粒是否完整,需要对图像中的每个集料颗粒进行遍历操作,效率较低;在集料下落过程中,集料会发生旋转,导致集料在前后图像中的轮廓不一致,影响轮廓匹配的成功率。
基于上述分析,本文对下料过程中的集料图像进行研究,寻找可行的动态集料级配视觉检测方法。针对图像边界处存在不完整颗粒和颗粒重复出现的问题,提出形态重建和反向跟踪的图像处理方法;将等效椭圆Feret短径作为等效粒径,分析集料的粒径分布;对像素尺寸与实际尺寸之间的关系进行优化,提高集料级配检测的准确性。
2 实验台的搭建及ROI的形态重建
2.1 检测实验台的搭建
检测实验台如图1所示。集料通过振动下料机均匀分散的落下,工业相机采用背光拍摄方式[11],对下料过程中的集料进行图像采集,并将图像数据传输给工控机进行粒径分析。使用的实验相机为合肥埃科光电科技有限公司的TS4MCL-180M/C高速工业相机,有效像素4×106,最高帧率180帧/s,镜头型号为HC2505A,焦距为25 mm。试验中的有效拍摄面尺寸为210 mm×210 mm。

图1 检测实验台的搭建Fig.1 The testing experimental bench
对运动状态下的集料进行图像采集,需要选择合适的曝光时间,根据集料下落的速度,曝光时间设为500 μs,采集的运动粗集料图像如图2所示。

图2 运动粗集料图像Fig.2 The image of the moving coarse aggregates
2.2 基于形态重建的ROI图像提取
首先对图像进行二值化处理[12],将集料颗粒与背景分离。在稳定的检测环境中,通常采用基于先验概率的阈值分割方法。在运动集料的图像采集过程中,存在部分集料颗粒下部分进入视场而上部分未进入视场,或下部分离开视场而上部分未离开视场的情况,导致图像上下界边缘处存在形态不完整的集料颗粒。如图3所示,在二值化图像的上边缘处,存在一颗不完整的集料颗粒。

图3 形态不完整的集料颗粒图像Fig.3 The image with an incomplete aggregate particle
若将不完整的集料颗粒纳入数据统计,会影响统计结果的准确性。为了避免这些集料颗粒对数据统计的影响,通过掩膜算子提取感兴趣(reqion of interst,ROI)图像,过滤图像上下边界处的集料颗粒,然后采用形态重建方法对ROI图像上下边界处的不完整集料颗粒进行形态修复,保证ROI图像中的集料颗粒都具备完整的形态。
2.2.1 基于掩膜的ROI提取方法
为了过滤图像上下边界处不完整的集料颗粒,本文通过掩膜算子对原二值化图像的上下边界进行遮盖。遮盖的高度由集料颗粒在图像中出现的最大像素高度决定。本文中,图像的分辨率为 2 048 pixel×2 048 pixel,视场大小为210 mm×210 mm,可得比例系数K:
(1)
在本工程中,粗集料的最大径不超过35 mm。通过比例系数K可得,粗集料在像素坐标中的最大径不超过341.33 pixel,考虑到特殊集料颗粒的存在,掩膜算子的遮罩高度h取400 pixel,即ROI上下边界范围设定为[400,1 648]。对图3进行ROI提取,设图3为g(x,y),掩膜算子为t(x,y),则ROI图像k(x,y)为:
k(x,y)=g(x,y)·t(x,y)
(2)
ROI提取效果如图4所示,图4(a)为掩膜算子,图4(b)为提取后的ROI图像。可以观察到,图4(b)中,ROI上下边缘处的集料颗粒形态被破坏。
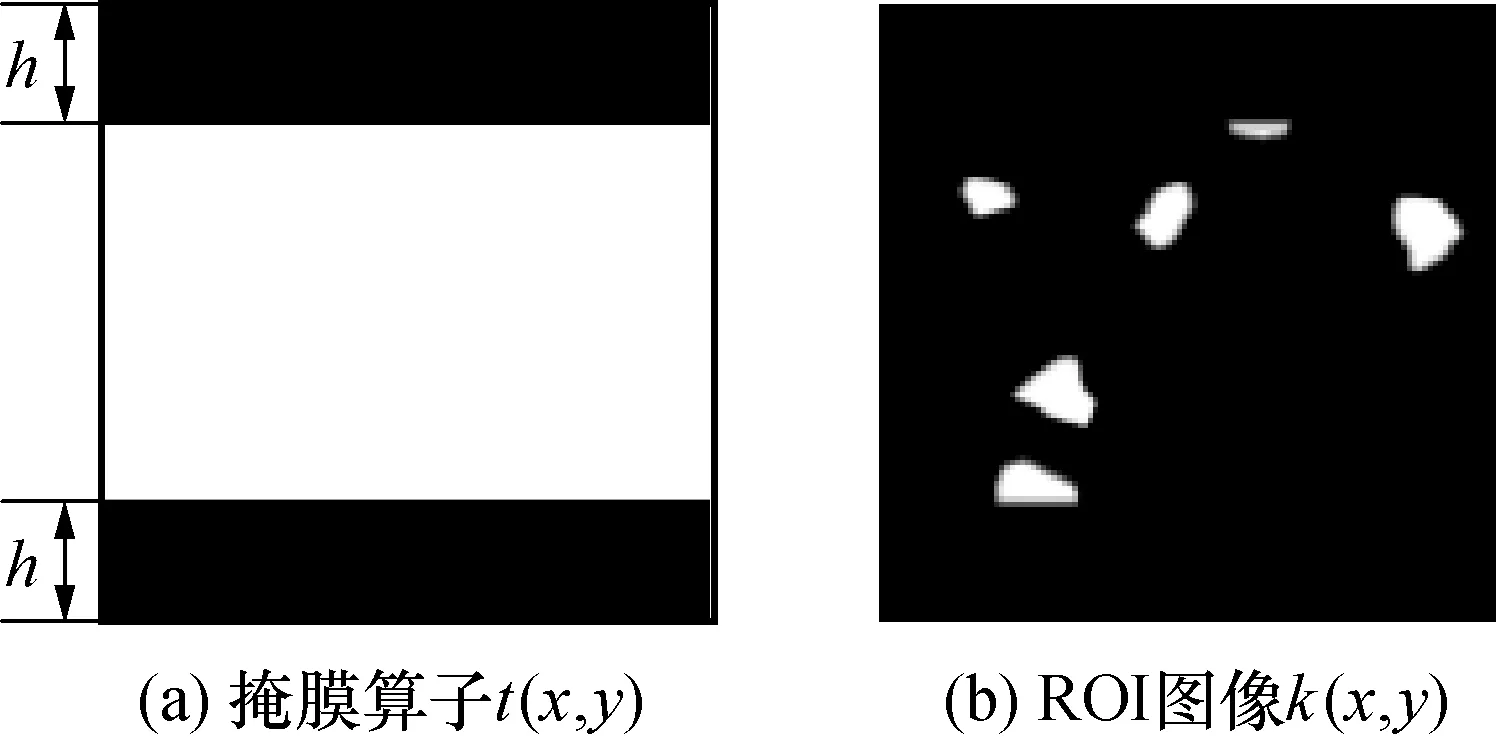
图4 掩膜提取ROI效果Fig.4 ROI image extraction
2.2.2 ROI边缘颗粒的形态重建
对于ROI图像中新出现的不完整颗粒,采用区域生长方法[13]对其进行形态重建。在ROI图像k(x,y)中,从ROI边界颗粒的任意一个像素开始,以二值图像g(x,y)为遮罩,根据4近邻准则向外填充像素,实现不完整颗粒的形态修复。图5为形态重建图,设图5(a)的4近邻算子为C(x,y)。
首先,4近邻算子从ROI上边界位置开始,在原二值化图像g(x,y)上自左向右移动。当4近邻算子在原二值图像中的位置为(n,m)时,其覆盖下的原二值化图像子区域为gn,m(x,y)。将4近邻算子与原二值化图像子区域进行矩阵点乘,得到填充算子d(x,y),计算公式为
d(x,y)=C(x,y)·gn,m(x,y)
(3)
将填充算子放置在ROI图像k(x,y)中的目标位置,并乘以目标位置中心的像素值得到新的填充算子D(x,y),其计算公式为
D(x,y)=k(n,m)·d(x,y)
(4)
令填充算子覆盖下的ROI子区域为α(k),将其与新填充算子D进行或运算,得到重构后的ROI子区域β(k):
β(k)=α(k)·D
(5)
然后,4近邻算子继续向右移动对该像素行进行重建。在完成该像素行的重建后,重新对其进行上述操作并多次循环,直至该像素行不再出现新像素,结束该像素行的重建。
最后,4近邻算子向上移动,重复以上操作,直至图像中不再出现新的像素,完成ROI图像上边界颗粒的形态重建。重复上述操作对ROI下边界颗粒进行向下的形态重建,最终重建得到的ROI图像如图5(b)所示,图5(b)中的每个集料颗粒都具备完整的形态。
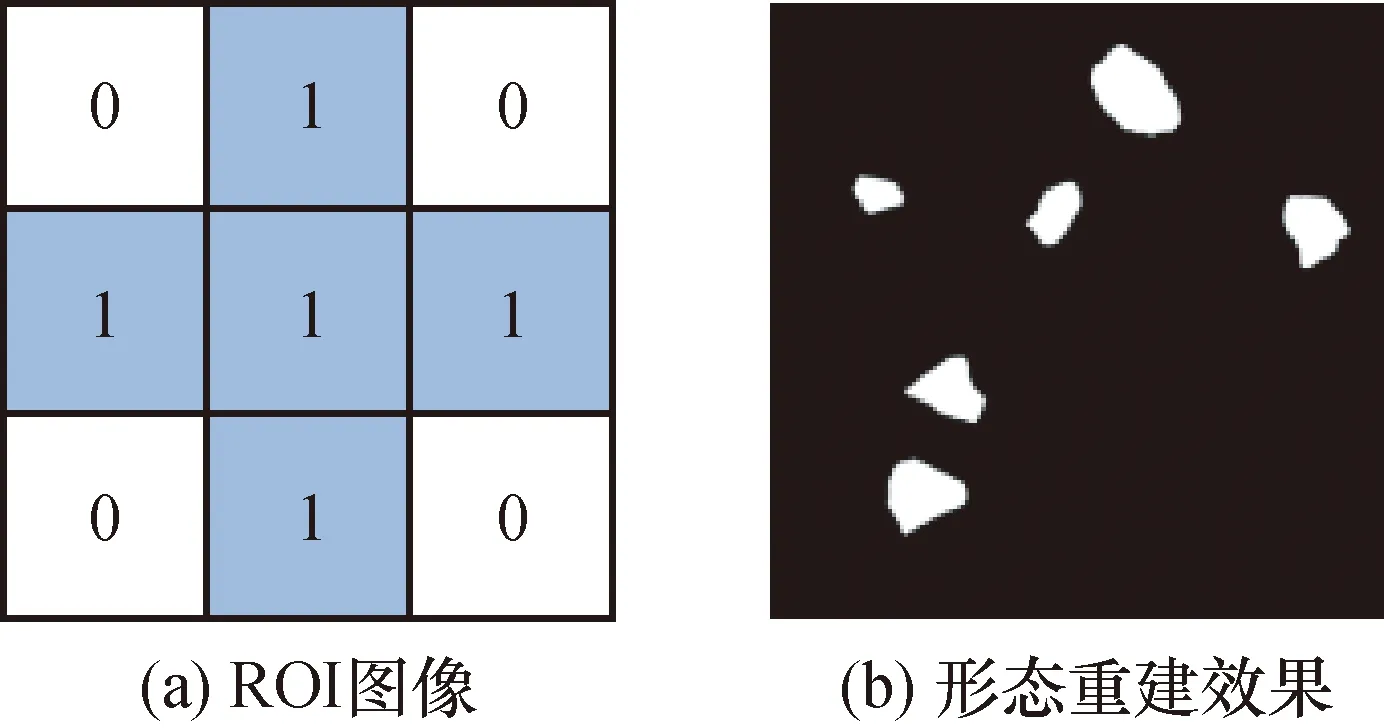
图5 形态重建Fig.5 Morphological reconstruction
3 基于反向跟踪的重复颗粒处理方法
3.1 图像帧采样间隔的确定
本文中图像采集帧率为149帧/s,在形态重建后的ROI图像序列中,集料颗粒会重复出现,包括在ROI图像提取过程中被滤除的集料颗粒。为了避免同一集料颗粒的重复统计,需要对连续的ROI图像进行间隔采样。每个集料颗粒的尺寸、下料初始速度各不相同,每个集料颗粒在图像中出现的次数存在差异,采样间隔过长将导致部分集料颗粒丢失。采样间隔过小将增加集料颗粒出现的次数,降低图像处理的效率。对100个集料颗粒在重建后的ROI图像中出现的次数进行统计,结果如图6所示。

图6 颗粒重复次数统计Fig.6 The number of every particle’s frames
由图6可知,同一个集料颗粒在连续的图像中至少出现10次,最多12次,图像帧采样间隔取为10帧,每间隔10帧ROI图像进行一次图像采样,保证每个集料颗粒必定出现在采样图像中,且至多出现2次。对于重复出现的集料颗粒,提出反向跟踪算法进行识别,避免数据重复统计。
3.2 重复颗粒区域的确定
为了确定重复颗粒出现的区域,对图像建立像素坐标系,如图7所示,○为首次出现的颗粒,△为重复出现的颗粒。图像左上角为原点,水平方向为x轴,竖直方向为y轴。第2次重复出现的颗粒均在图像下方,即其质心坐标y值较大。

图7 重复颗粒分布情况Fig.7 Particle distribution
图7中,图像由上至下被划分为检测区和重复颗粒识别区两个区域。重复颗粒识别区中的集料颗粒需要进行识别,判断其是否为重复颗粒,是反向跟踪算法的识别对象;检测区中的集料颗粒为首次出现的颗粒,是算法的匹配对象。
为了确定检测区域和重复颗粒识别区域的边界线,需要对第2次出现在采样图像中的集料颗粒进行坐标分析,将其最小质心y坐标作为参考数据。集料颗粒的质心y坐标数据统计如图8所示。

图8 颗粒重复出现位置预测统计情况Fig.8 Recurring particles’y-coordinate data.
在统计数据中,重复出现的集料颗粒的最小的质心坐标ymin=1 282.49 pixel。本文以1 250 pixel分界线,若颗粒目标的质心坐标y值小于 1 250 pixel,则为检测区中的颗粒,若y值大于1 250 pixel,则为重复颗粒识别区中的颗粒,如图9所示。

图9 区域划分情况图Fig.9 Regional division
区域划分后,对于检测区图像中的集料颗粒,直接进行粒径分析;对于识别区图像中的集料颗粒,需要进行反向跟踪,与上一个检测区图像中的集料颗粒匹配,判断其是否为重复出现的集料颗粒。若是,则将前后图像中的两次粒径结果取较大值,若不是,则直接进行粒径分析。
3.3 反向跟踪方程
下料口位于视场上方距离为y,集料在离开下料机进入下料口后,在竖直方向上近似为匀加速直线运动,初速度为v0,算法根据颗粒在第N+10帧图像中的位置,以及前后间隔10帧图像之间的固定时间变化Δt,推测颗粒在第N帧图像中出现的位置,为目标匹配提供位置推测基础。颗粒的竖直方向位置变化与时间的关系如图10所示。
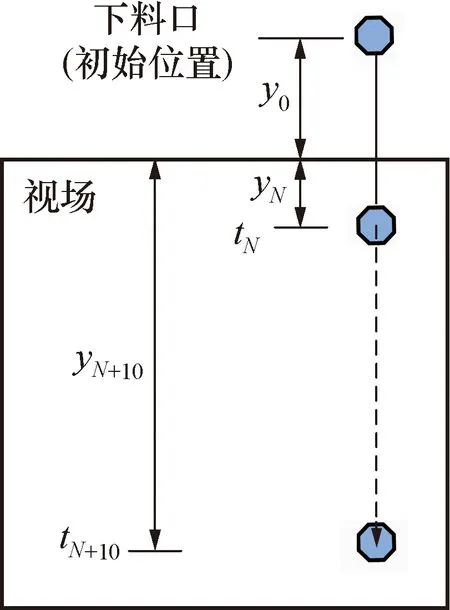
图10 颗粒位置与时间关系图Fig.10 Particle position and time diagram
图10中,yN为颗粒在第N帧中出现的竖直位置,tN为颗粒从下料口运动至yN处所用的时间,根据初速度v0、加速度g以及时间tN,可得到竖直方向位移yN,同理得到yN+10:
(6)
(7)
将Δt=tN+10-tN代入公式(7),经整理可得到yN关于yN+10的表达式:
(8)
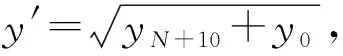
(9)
根据公式(9),对80组(yN+10,y′)组数据进行分析,采用数据拟合方法建立y′与yN之间的关系[14]。本系统中,下料口位于视场上方50 mm,由公式(1)将y0转化成像素距离为487.80 pixel,得到二次拟合结果如图11所示,二次函数如等式(10)所示。由试验数据分析,二次拟合函数的最大误差δmax=46.475 pixel。
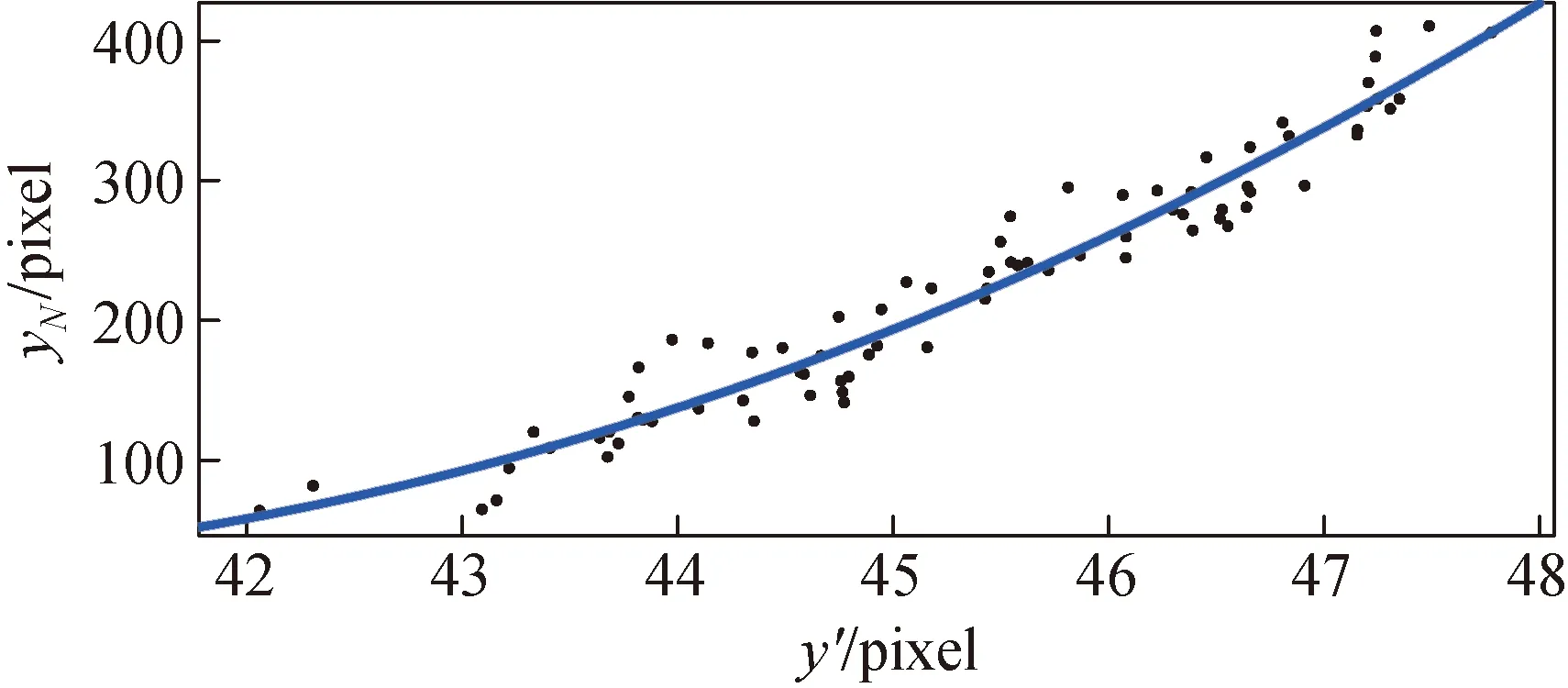
图11 二次函数拟合效果Fig.11 Quadratic fitting function.
11 062.75
(10)
在实际下落过程中,目标颗粒在水平方向上同样存在位移。为避免水平方向的位移对位置跟踪的影响,本文对上述颗粒的80组水平方向位置移动Δx数据进行分析,如图12所示。
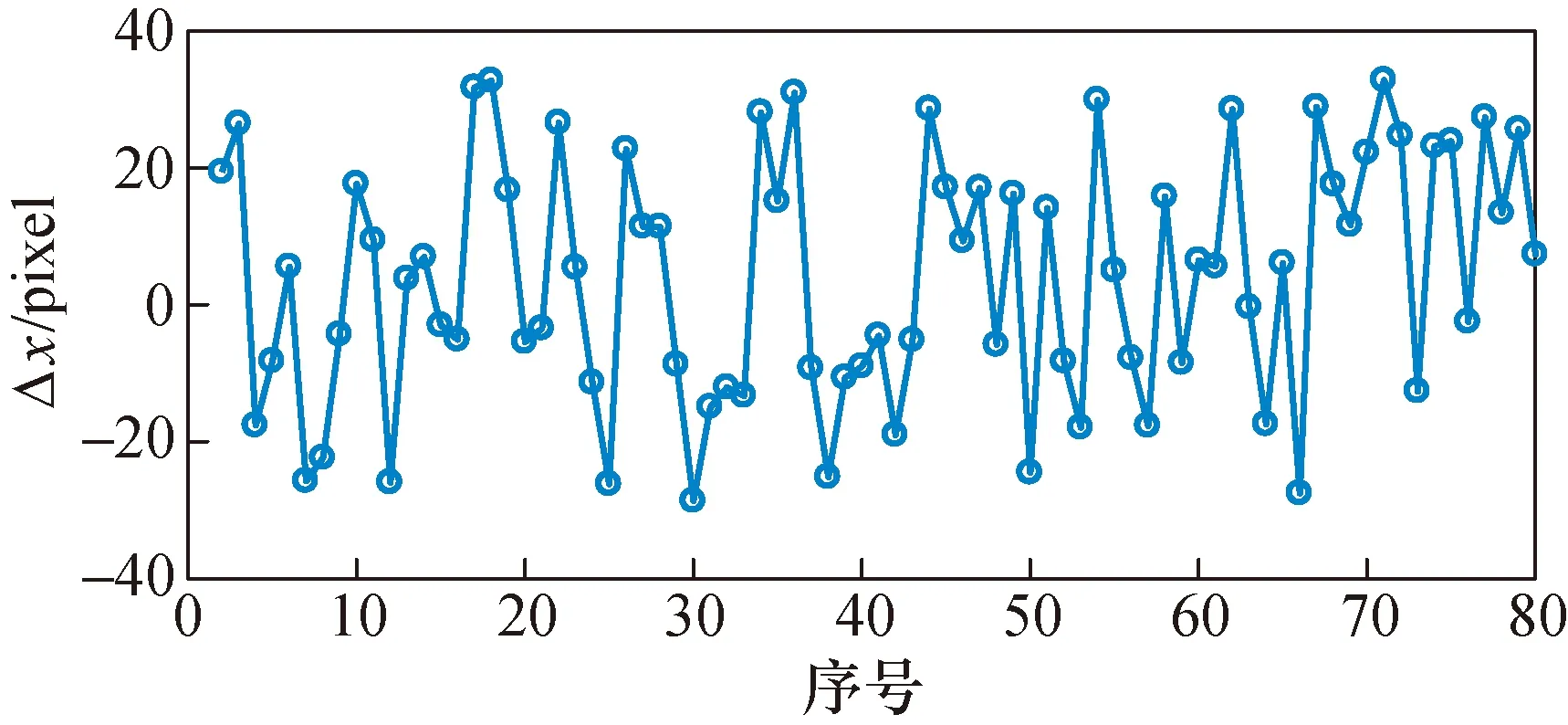
图12 水平位置移动距离统计图Fig.12 Statistical of horizontal moving distance
目标颗粒在下落运动过程中,水平方向位移绝对值最大|Δxmax|=32.83 pixel,小于竖直方向上的最大误差δmax,可认为
xN=xN+10
(11)
综上分析,间隔10帧的图像中,同一集料颗粒在第N帧与第N+10帧的位置关系如式(10)和式(11)所示。
3.4 基于接触式关联门的反向跟踪
根据式(10)和式(11),基于第N+10帧识别区中集料颗粒的坐标,可以反向推测出集料颗粒在第N帧图像检测区中出现的位置,如图13所示。算法以反向推测位置为圆点,以半径d设置圆形关联门,在关联门内搜索到目标即为匹配成功,判定该颗粒第2次重复出现;反之,判定为首次出现,为非重复颗粒。
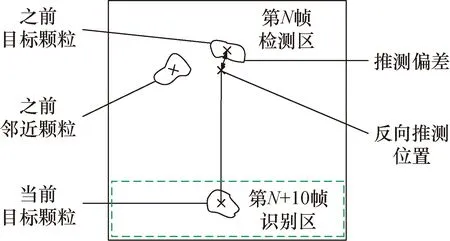
图13 目标匹配分析示意图Fig.13 Target tracking diagram
图13中,集料颗粒的实际位置与反向推测位置存在偏差,其附近可能存在其他颗粒,这些因素要求关联门半径不能过大或过小。由竖直方向最大误差以及水平方向最大位移可得最大预测偏差:
(12)
考虑最大预测偏差以及邻近颗粒的影响,设置关联门半径略大于最大预测偏差,其为70 pixel,搜索方式采用接触式,在跟踪匹配过程中,关联门与任意目标发生接触,即为匹配成功,反之,匹配失败。匹配示意图如图14所示。
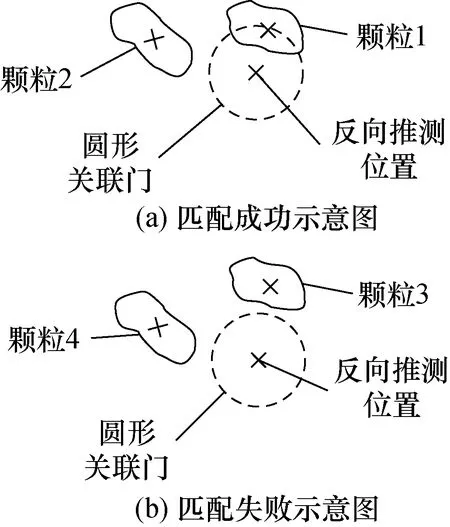
图14 反向匹配示意图Fig.14 Reverse tracking diagram
在图14(a)中,关联门与颗粒1接触,即被测目标与颗粒1匹配成功,为同一颗粒;在图14(b)中,颗粒3、颗粒4均与关联门无接触,则被测目标无匹配对象,为非重复出现颗粒。
算法跟踪识别效果如图15所示。图15(a)和图15(b)中,颗粒a和颗粒f为同一个颗粒目标。颗粒在下落过程中存在旋转,导致在前后图像中的成像颗粒a与颗粒f轮廓不同,此时轮廓匹配会失效,本文算法根据图15(d)中颗粒f的位置进行反向跟踪,在图15(c)中设置关联门,此时颗粒a与关联门接触,成功匹配到颗粒a,能顺利识别出颗粒a与颗粒f为同一颗粒。
4 集料粒径分布计算方法
4.1 等效粒径表征参数
集料颗粒常用的表征参数有等效矩形长短轴、等效椭圆长短径以及等效椭圆Feret短径[15],本文选择与筛分法结果最为相近的等效椭圆Feret短径作为等效粒径[16]。如图16所示,以集料图像的最大Feret径dF为长轴,作与集料图像面积相同的等效椭圆,其短径de即为等效椭圆Feret短径。
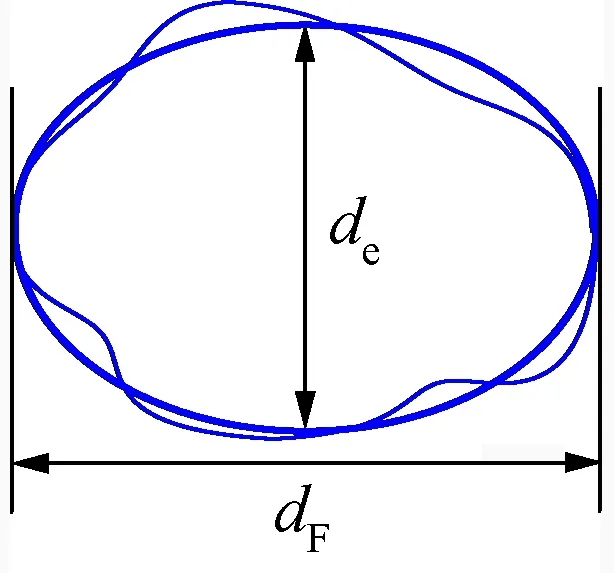
图16 等效椭圆Feret短径Fig.16 The Feret minor axis of equivalent ellipse
对于未重复出现的颗粒,其等效椭圆Feret短径即为粒径结果;对于重复颗粒,其前后2次成像的粒径较大值即为最终粒径结果。
4.2 尺寸转化关系优化
在集料图像采集过程中,由于集料粒径不同,每个集料颗粒的成像平面也不同。以小球成像分析为例(见图17),大尺寸小球的成像平面比小尺寸小球的成像平面更靠前。在图像获取过程中,为了获得清晰的集料图像,通常将中等尺寸集料颗粒的下落平面作为拍摄平面。在其他条件不变的情况下,物距越小,公式(1)中的比例系数K越小。尽管在实际情况中,不同尺寸的集料颗粒的下落平面差异较小,但直接根据公式(1)计算集料的粒径会引入一定的误差。
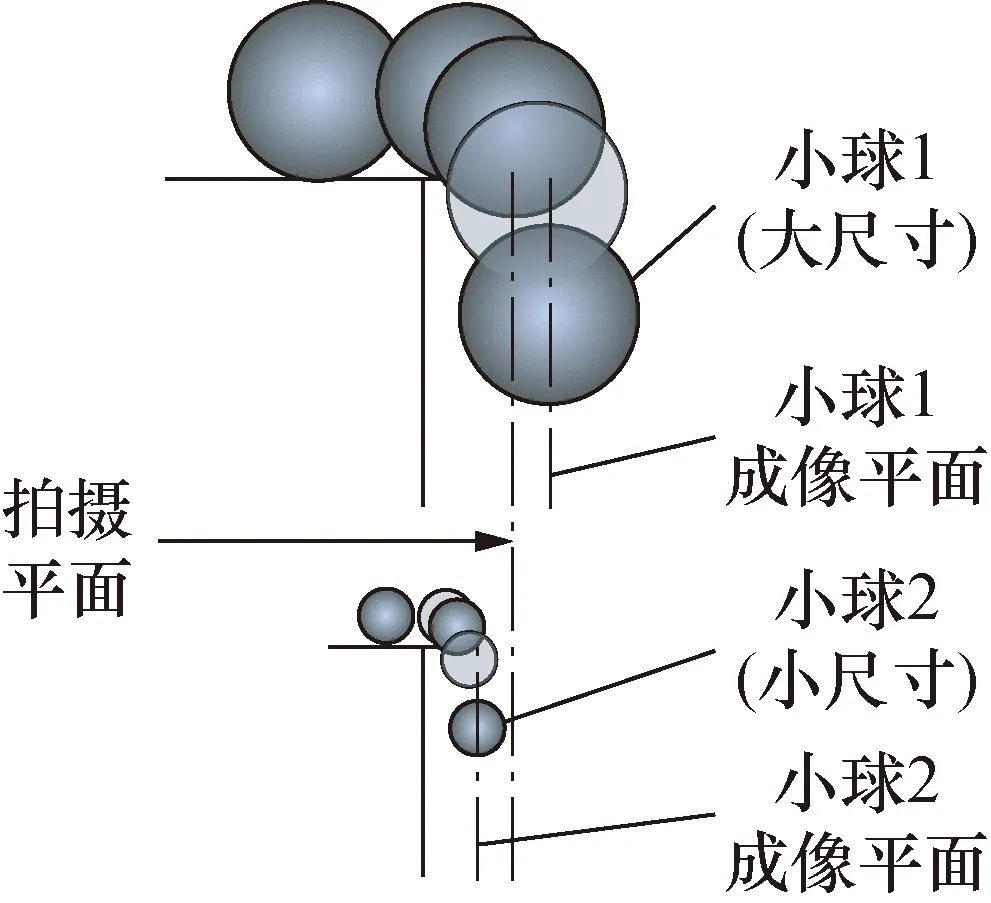
图17 小球成像分析Fig.17 Globule imaging analysis
为了探究小球的像素尺寸与实际尺寸之间的关系,对小球尺寸进行了定性分析,如图18所示。
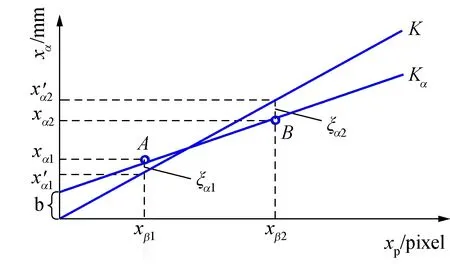
图18 尺寸变换分析Fig.18 Analysis of dimensional transformation relationship
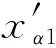
为了减小此类计算偏差对粒径分布结果的影响,本文对K进行修正,并引入偏置b,使粒径计算结果更接近真实情况。据此,像素大小与实际大小的关系可以表示为:
xα=Kxβ+b
(13)
式中:xβ、xα分别为颗粒的实际尺寸和像素尺寸。
为了确定式(13)中最佳的K和b,选择4种规格的集料区间(4.75~9.5 mm,9.5~16 mm,16~19 mm,19~26 mm)进行实验,每个规格的集料样本数为200,使用不同的K和b计算集料的粒径,并根据式(14)计算不同K和b下集料级配的准确率P:
(14)
式中:ni是第i规格颗粒的检测数量;mi是第i规格颗粒的实际数量。级配准确率分布如图19所示,当K=0.093 6,b=0.67时,集料级配的准确率P=0.936 25。
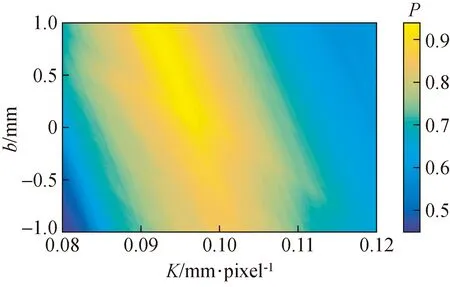
图19 粒径分布准确率Fig.19 The accuracy under different combinations of K and b
5 结果分析
5.1 反向跟踪的识别率
本文对500颗粗集料进行图像采集,连续采集7 147帧图像,从中间隔采样715帧ROI图像,人工方式发现有104个目标颗粒重复出现2次。分别采用轮廓匹配法、反向跟踪法对图像中的重复颗粒进行识别,结果如表1所示。
由表1可知,与轮廓匹配法相比,本文的反向跟踪法对重复出现的集料颗粒的识别率更高。
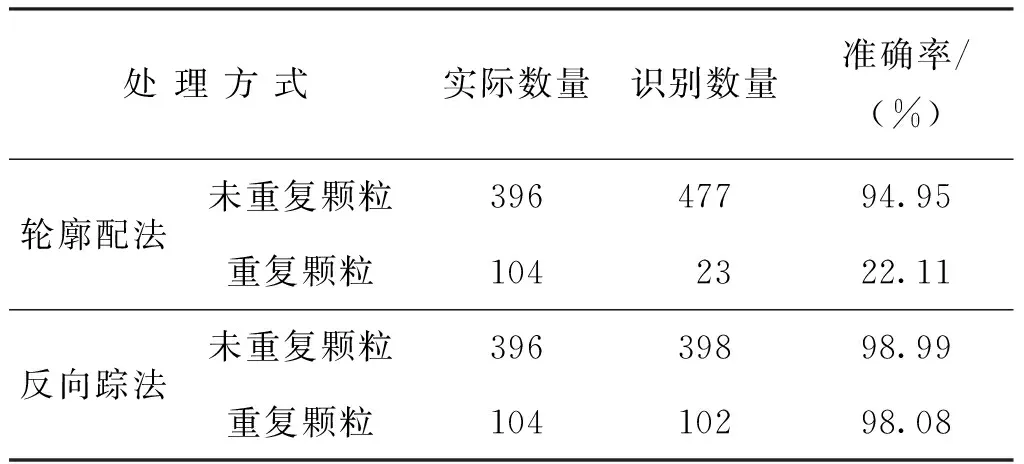
表1 目标颗粒识别比较Tab.1 Target particle recognition comparison
5.2 集料粒径计算的的准确性
为了验证等效粒径的计算方法,选择了4种规格(4.75~9.5 mm,9.5~16 mm,16~19 mm,19~26.5 mm)的集料样本进行实验,每种规格的集料数量为200颗,分别通过方法1(xα=Kxβ,K=0.102 5)和方法2(xα=Kxβ+b,K=0.093 6,b=0.67)计算集料粒径进行级配检测,结果如表2所示。
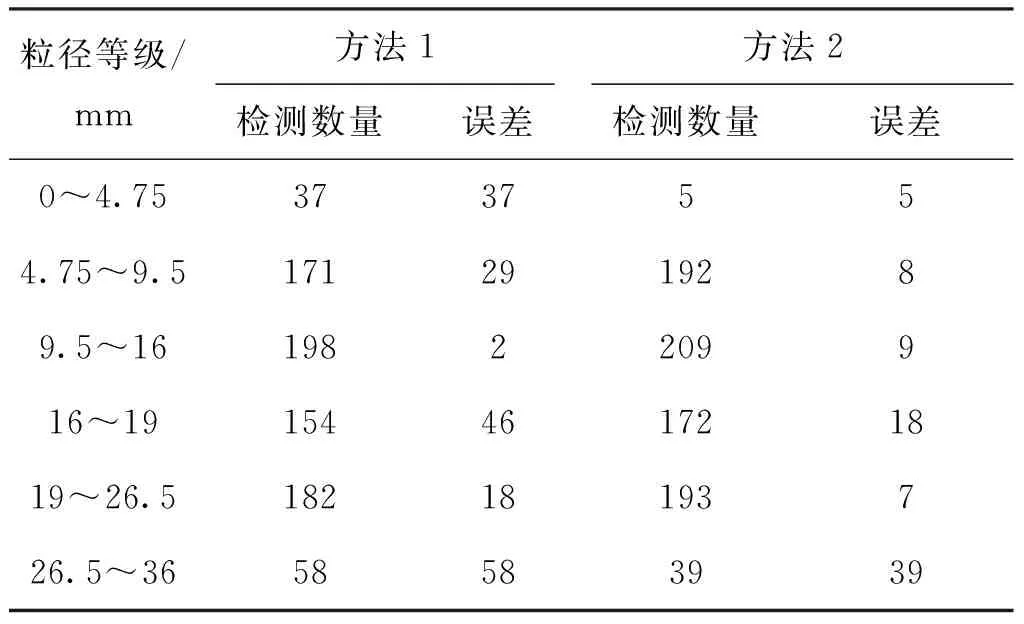
表2 粒径分析结果Tab.2 The results of aggregate particle size distribution
从表2可以看出,根据第2种方法计算的颗粒尺寸进行级配的结果比第2种方法更准确,其集料级配检测的准确性为95.59%。
6 总 结
本文针对粗集料的级配检测,提出了集料在运动状态下的图像检测方法。使用基于掩膜的ROI区域提取方法,结合形态重建方法,解决了图像中存在不完整颗粒的数据统计问题;使用基于接触式“关联门”的反向跟踪算法,对采样图像中的集料颗粒进行跟踪识别,避免了前后采样图像中同一集料颗粒被重复统计的情况;使用等效椭圆Feret短径作为等效粒径对集料进行粒径分析,并对像素尺寸和实际尺寸的转换关系进行优化,提高级配结果的准确性。实验证明,反向跟踪算法对重复出现的集料颗粒识别的准确率为98.08%;集料级配检测的准确率为95.59%。

