白光干涉测量系统的测量不确定度评定
蔡潇雨,魏佳斯,孙恺欣,3,刘 娜,3,张学典,庄松林
(1.上海理工大学 光电信息与计算机工程学院,上海 200093;2.上海市计量测试技术研究院,上海 201203;3.上海计测信息科技有限公司,上海 200234)
1 引 言
随着纳米技术的发展,纳米材料或器件的表面形貌特征对其技术性能有重要的影响,同时对微纳米测量技术也提出更高要求,为此,逐渐发展起来了相应的微纳米测量仪器[1~3]。典型的有扫描探针显微镜、光学干涉显微镜、微触觉坐标测量机、扫描电子显微镜、透射电子显微镜等。其中,基于白光干涉原理的测量仪器具有非接触、大量程、高精度、高效率的特点,广泛应用于新材料、半导体、光学器件等精密测量中[4~7]。
干涉显微测量方法是利用光波干涉原理测量表面轮廓,通过测量受物体表面形貌调制而变化的光程差在整个光场中的空间起伏变化,解算得到表面形貌。白光干涉测量技术是由单色光干涉测量技术演变而来,且由于相较单色光白光具有更短的相干长度,不会出现条纹影像互相混叠的情况,零级条纹对比度强,克服了传统单色光相移干涉术中相位模糊的问题[8~10]。
随着白光干涉测量仪器的发展,尤其是图像采集技术与处理软件的迭代,白光干涉测量系统从最开始的单一高度(Z方向)测量完善到了三维表面形貌的测量与表征。为了进一步研究白光干涉测量系统的计量特性,保证其测量结果的量值可靠,对白光干涉测量系统的测量不确定度进行分析与评定是非常有必要的,但目前尚无针对该类仪器的计量规范或国家标准详细指导评定方法。
本文对WLIS的测量模型、误差来源及其引入的测量不确定度分量进行了详细地分析,结合实验结果,得到了WLIS三维测量的不确定度。
2 测量原理与系统组成
基于白光干涉的测量原理是提取样品表面的光强值,即白光光谱中不同频率光波发生干涉后的合成光强,其信号表示成一个幅值经高斯函数调制的余弦信号;当测量光束照射到被测样品表面与参考光束到参考镜面的光程差为零时,各光波的零级条纹完全重合,在被测样品表面达到光强最大值;经过处理后获得表面形貌和高度信息[11,12]。
白光干涉测量系统通常由光学干涉模块、光学传感模块、运动测量模块和控制模块组成。光学干涉模块主要是由白光光源、干涉物镜、镜筒等组成干涉光路,如图1所示。白光光源发出的光束经过偏振分光镜1分为两束,其中一束实现白光干涉:该束光线首先被镀有半透半反膜的分光镜2进一步分为两路,一路光反射到参考反射镜,后反射到物镜; 另一束则透过分光镜2投射到被测样品表面,经样品表面反射后回到物镜,两束光在物镜视场中会合发生干涉[13]。光学传感模块主要通过CCD或CMOS图像传感器采集带有干涉信号的图像。运动测量模块通常包括用于对焦、循迹的X、Y、Z三轴粗动平台、用于扫描测量Z轴精密微动台,扫描过程中得到的空间扫描位置会与光学传感模块获得的干涉信号相映射[14]。控制模块中包括下位控制器和上位机,实现系统的控制和数据传输、软件处理与分析。白光干涉测量系统组成见图2所示。
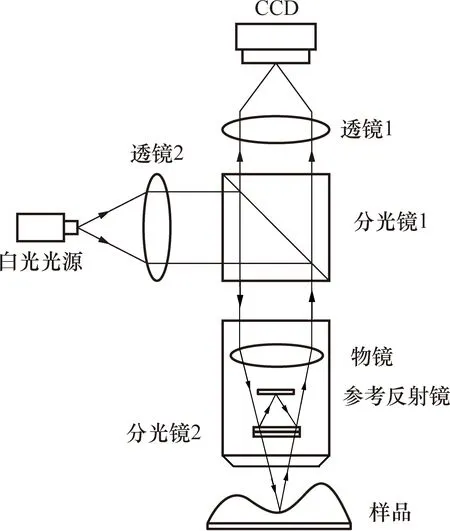
图1 白光干涉测头光路示意图Fig.1 Beam path schematic of the white-light interferometer

图2 WLIS组成示意图Fig.2 Schematic of WLIS components
3 测量模型
3.1 线间隔的测量模型
微纳米线间隔(micro/nano pitch)是具有微纳米级准确度和均匀性的周期性刻线[15],可以是一维形式和正交的二维形式,以相邻几何结构的间距表征刻线间隔。微纳米线间隔是典型的横向长度的计量传递标准。
考虑各影响分量后,白光干涉测量系统测量线间隔的模型为:
(1)
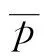

图3 φxz示意图Fig.3 Schematic of φxz
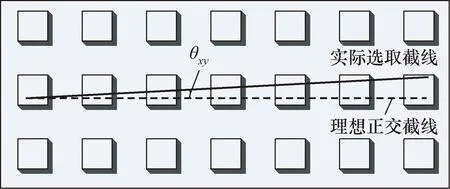
图4 θxy示意图Fig.4 Schematic of θxy
3.2 台阶高度的测量模型
微纳米台阶高度是具有微纳米尺度量值的台阶状表面几何结构形式,用来表征垂直高度(深度)[16],是典型的纵向高度测量的计量传递标准。
考虑各影响分量后,白光干涉测量系统测量台阶高度的模型为:
(2)

4 测量实验与测量不确定度评定
4.1 复合型微纳米样板测量实验
实验选用了VLSI公司STS2-1800P型号的复合型微纳米标准样板,台阶高度标称值为180 nm,一个区域的二维线间隔标称值为5 000 nm,见图5。
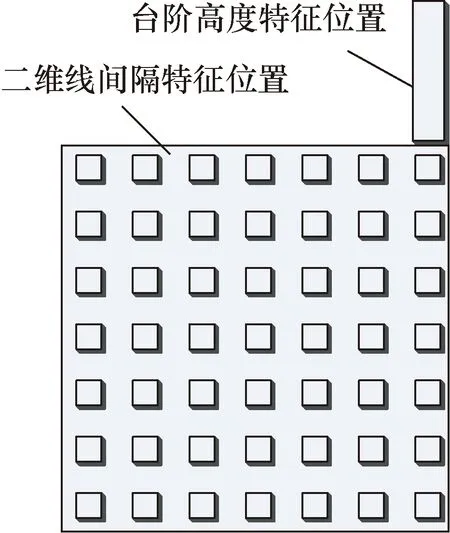
图5 STS系列标准样板拓扑图Fig.5 Topological map of STS specimen
使用白光干涉测量系统50×放大倍率物镜对标准样板的平均线间隔和台阶高度分别进行重复性测量实验。
定位至样板二维线间隔待测范围内中心位置附近,重复扫描4次;在每次扫描所得的三维结构图的同一位置附近,提取与线间隔方向垂直方向的轮廓,如图6,提取3次,每条轮廓包含6个以上线间隔周期;通过重心法计算平均线间隔pi[17,18],获得线间隔数据,见表1。
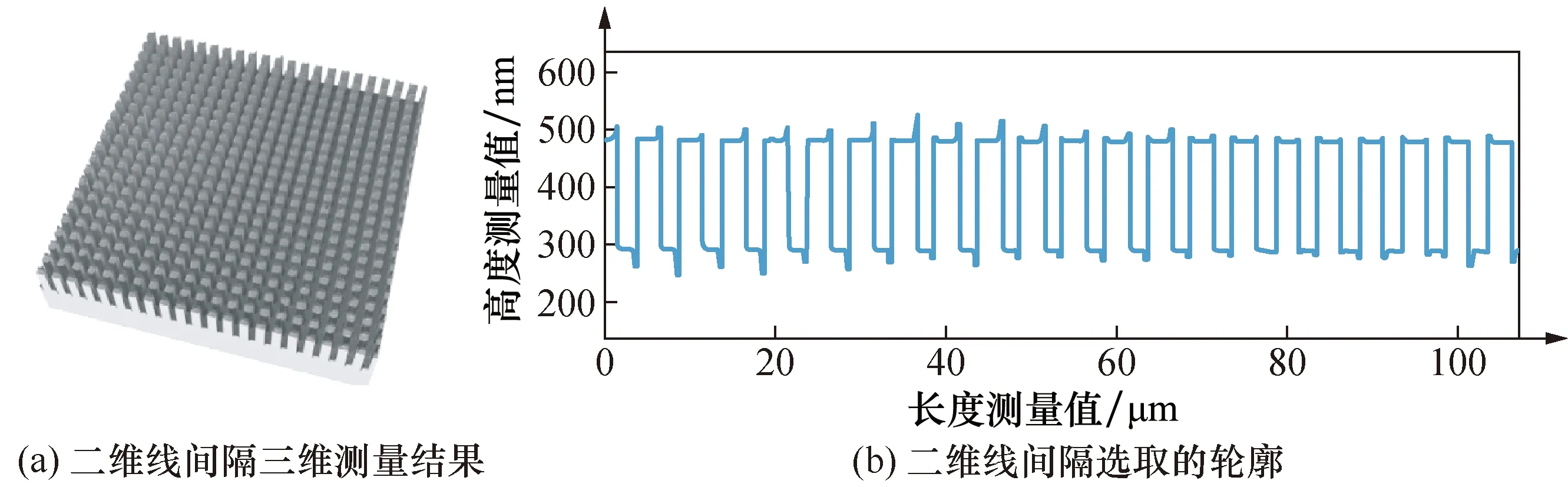
图6 线间隔测量结果Fig.6 Results of pitch measurement

表1 线间隔重复测量数据Tab.1 Measured values of the pitch under repeatability condition nm
定位至样板台阶高度区域中点附近,重复扫描4次;在每次扫描所得结构图中间位置选取3条台阶轮廓,如图7;计算台阶高度[19, 20],获得台阶高度数据如表2所示。

图7 台阶高度测量结果Fig.7 Results of step height measurement

表2 台阶高度重复测量数据Tab.2 Measured values of the step height under repeatability condition nm
4.2 线间隔的测量不确定度评定
基于WLIS线间隔测量模型式(1),本文对系统测量线间隔时的不确定度来源进行了分析。
4.2.1 光学部件引入的测量不确定度
光学部件在系统横向测量时引入的不确定度主要来自[21]:光学干涉模块中放大倍率的误差、光学传感模块中图像传感器感光面与干涉平面不平行引入的误差、图像传感器芯片的像元尺寸不均匀等。
1)光学放大倍率引起的测量不确定度分量uM
光学部件放大倍率由干涉物镜和镜筒决定。考虑在白光干涉测量系统中,系统的横向测量标尺在测量前通过横向特征尺寸的标准样板进行了标定,修正了系统放大倍率的不准确引入的误差,因此将光学放大倍率引起的测量不确定度分量uM不单独计,并入由标定校准引入的不确定度分量ucal中。
2)图像传感器感光面与干涉平面不平行引入的不确定度uxz
图像传感器感光面与干涉平面的夹角相当于测量标尺与被测平面之间的夹角,从而引入了一个的余弦误差。类似光学放大倍率不准确带来的误差,该误差也通过对测量系统的校准得到了一定程度的修正,不单独计其带来的不确定度。
3)标定校准引入的不确定度分量ucal
WLIS投入使用前,使用了校准值为3 000 nm、扩展不确定度为2 nm(k=2)的线间隔标准对系统进行了横向测量标定。考虑由于校准标准、方法和结果处理的不完美,尤其是标准样板的不确定度,仍会存在一定误差。则由校准标定不准确引入的不确定度分量:
(3)
式中:Ucal为校准用标准的扩展不确定度;Pcal为校准值。
4)图像传感器像元尺寸不均匀性引入的不确定度upix
根据图像传感器的技术手册,图像传感器像元尺寸扩展不确定度为1%,包含因子为2.45(服从三角分布)。由此可得图像传感器像元尺寸不均匀性的相对标准不确定度为:
(4)
4.2.2 横向测量数显分辨力引入的不确定度
系统横向测量的数显分辨力为0.1 nm,假设其满足均匀分布,由其引入的不确定度为uR:
(5)
4.2.3 测量重复性引入的不确定度

(6)

在评定不确定度时,取uR和ur两者中大者计入,即取测量重复性引入的不确定度ur。
4.2.4 被测样板温度变化引入的不确定度
被测样板温度变化引入的不确定度uT由样板材质和实验环境温度变化情况决定。样板材质热膨胀系数α为0.5×10-6K-1,实验室环境温度变化量ΔT为1 K。热膨胀带来的变化量与其它不确定度分量相比较小,故被测样板温度变化引入的不确定度可忽略不计。
4.2.5 被测样板均匀性引入的不确定度
为更好地研究白光干涉测量系统的自身特性,在评定其测量不确定度时,实验尽可能地在被测样板原位进行重复测量,即重点考察仪器的测量重复性,而尽量避免被测样品的不均匀性带来的误差。故样板均匀性引入的不确定度分量uS可忽略不计。
4.2.6 样板测量角度引入的不确定度
在通过实验确定正交扫描角度后,样板安放与测量扫描方向在横向产生的倾斜角度一般可控制在0.75°内。假设其满足均匀分布,该角度引入的不确定度分量uxy由式(7)计算得:
(7)
表3为线间隔测量时不确定度分量汇总表。

表3 线间隔测量不确定度分量Tab.3 Uncertainty components in pitch measurement
被测量值的各输入量之间不相关,因此X、Y方向线间隔的合成标准不确定度分别为:
(8)
(9)
式中:uc(Px)、uc(Py)分别为X、Y方向线间隔测量的合成标准不确定度。
4.3 台阶高度的测量不确定度评定
基于WLIS台阶高度测量模型式(2),本文对系统测量台阶高度时的不确定度来源进行了分析。
4.3.1 测量运动平台引入的不确定度
根据白光干涉测量系统测量原理和测量过程,测量运动平台引入的不确定度主要来自微动平台的各项误差,包括其分辨力、非线性、驱动电压放大器的噪声和纹波等。
1)由测量运动台非线性δL引入的[23]相对不确定度分量uL
实验用WLIS的测量运动平台非线性为0.03%,按均匀分布,由其引入的不确定度分量为:
(10)
2)由测量运动台分辨力误差δRpzt引入的不确定度分量uRpzt
实验用WLIS的测量运动平台分辨力误差为0.65 nm,假设其满足均匀分布,故由其引入的不确定度分量为:
(11)
3)由测量运动台纹波噪声引入的不确定度分量uN是由电压波动引起的高频分量,其影响远小于测量运动台的非线性和分辨力引入的不确定度,故可忽略不计。
4)由测量运动台温漂引起的[24]不确定度分量uTpzt
由于实验温度变化范围控制在1 ℃,且实验用测量运动平台经过了温度补偿,其因温度变化引起的不确定度可忽略不计。
4.3.2 图像传感器光强采集能力引入的不确定度
由图像传感器光强采集能力与其能探测到的最小光强变化ΔI有关,[21,25~27]该值由图像传感器采样位数N决定:
(12)
式中:Imax、Imin分别为可探测到的最大光强和最小光强,Imax-Imin对应的相位变化量为π,能检测到的最小相位变化为:
(13)
故被测表面的最小纵向高度变化量Δh:
(14)
式中:λ为白光中心波长,550 nm;图像传感器采样位数N为8位。
假设可分辨的纵向高度可能值满足均匀分布,故由图像传感器光强采集能力引入的不确定度uI为:
(15)
4.3.3 被测样板均匀性引入的不确定度
类似线间隔的实验与不确定度分析,台阶测量实验亦在被测样板原位进行重复测量,故样板均匀性引入的不确定度分量uS可忽略不计。
4.3.4 测量重复性引入的不确定度
类似线间隔测量中测量重复性引入的不确定度评定,用所测得的台阶高度的算术平均值作为被测量的最佳估计值,重复性引入的不确定度ur为:
(16)
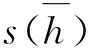
表4为台阶高度测量时不确定度分量汇总表。

表4 台阶高度测量不确定度分量Tab.4 Uncertainty components in step height measurement
被测量值的各输入量之间不相关,因此台阶高度测量的合成标准不确定度uc(H)为:
(17)
5 结 论
依照JJF 1001-2011《通用计量术语及定义》技术规范,测量所得平均值和评定得出的不确定度共同组成了当次实验的测量结果。本次实验WLIS横向测量时合成不确定度21 nm,纵向测量时合成不确定度0.4 nm,达到了亚纳米水平,且远优于横向测量的不确定度,印证了WLIS在纵向高度测量时能够达到纳米甚至亚纳米精度。同时,通过不确定度评定得出影响测量结果的因素来自图像传感器(如CCD)、测量运动平台(如压电陶瓷微动台)、仪器测量重复性等,其中测量重复性较大程度上受软件图像数据处理算法准确性和稳定性的影响。
由此可以得出,在WLIS的研究与应用中,可以通过提高图像传感器像素均匀性和采样位数、提高系统测量运动台的定位精度和线性度、优化软件白光干涉条纹峰值提取算法等途径,减少相应的不确定度分量,从而提高系统整体的计量特性。

