基于多视角区域生长的复杂点云模型分割
孔德明,张 娜,王书涛,史慧超
(1. 燕山大学 电气工程学院,河北 秦皇岛 066004;2. 北京化工大学 信息科学与技术学院,北京 100029)
1 引 言
点云模型分割是医学研究、模式识别、机器人环境认知、逆向工程等领域中一项关键且繁琐的技术。作为目标识别的基础,其实质是将具有相似特征属性的点划分入同一区域,不同特征的点归入相互独立的集合,从而依据各区域内点集的特性选取相应处理方式对其分而治之,使得后续有针对性地处理更加精准高效。然而,现实场景中物体逐渐趋于复杂化,应用现有的点云分割技术已不能满足快速、高精度的要求。因此,如何在高冗余度且无序不均的数据点中,迅速提取关键点并进行有效处理是当前重点研究的内容。
区域生长作为点云分割领域中的经典分割算法,因其算法原理简单且易于实现,广泛应用于各种场景中。Yi B等[1]通过区域生长算法获取点的恰当局部区域,同时利用基本基元的中层参数,指导各点法线参数的修改和曲面类型的迭代检测;Rabbani T等[2]提出一种加入平滑条件约束的区域生长算法对密集管道场景进行分割,但应用于复杂场景时分割效果欠佳;李仁忠等[3]将曲率最小的点设置为种子点,以拟合曲面与种子面法向量夹角是否超出阈值作为生长准则实现点云分割,但该算法的阈值需要测试选取,故分割的稳定性不足;郭保青等[4]利用基于法线一致性原则的区域生长算法对铁路场景中不同类物体进行分割,并利用VFH获取单个物体特征信息;卢维欣等[5]借助主成分分析法提取建筑物点云的最优特征,依据有效区域内点的特征属性确定生长规则实现建筑物平面的精确分割。
现有的区域生长分割算法虽能实现点云场景的完整分割,但种子点选取的高随机性、局部特征变化平缓区域点云特征模糊导致的生长规则难确定性使得分割效果有一定的局限。本文在传统区域生长算法的基础上,提出了一种基于多视角区域生长的复杂曲面结构模型分割方法,通过在多视角下建立点云与距离图像的一一映射关系,获取各个待分割区域内的种子点并将其作为生长中心;以网格法向量偏移角度和各点之间的距离度量作为生长判别标准,同时利用KNN算法剔除分割过程中的异常点,实现复杂点云模型的合理分割。
2 算 法
本文的算法实施流程如图1所示。输入点云数据采用构网的方式生成连续规则的网格结构,计算网格结构中各三角面片的法向量,从而基于网格法向量方向相异性原则将复杂点云模型进行初分类;依据目标分割面的特征多次选取恰当视角建立点云与距离图像的映射关系;采用Canny算子获取各个面的边缘信息并生成独立连通域,进而根据映射关系,计算各连通域内重心坐标在三维空间中的对应点,将此点作为种子点;以种子点为生长中心,利用区域生长算法实现模型的完整分割。
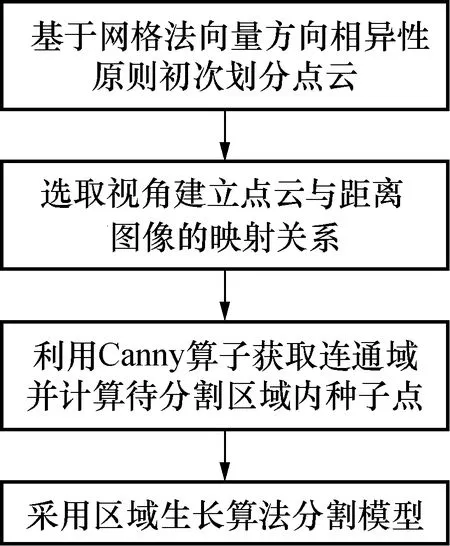
图1 算法流程图Fig.1 Flow chart of algorithm
2.1 基于网格法向量的点云初次分类
为了更好地描述非结构化点云数据的特征,构建点云模型的网格结构并计算生成三角面片的法向量[6,7],依据三角面片各顶点的坐标数据,计算由任意1个顶点指向其余2顶点的两相异法向量,得到向量V1和向量V2,两向量间的夹角用γ表示,解算两向量的向量积得到该三角面片的法向量D0(d01,d02,d03):
|D0|=|V1×V2|=|V1|·|V2|sinγ
(1)
对所得法向量进行归一化处理,使不同维度之间的特征在数值上具有一定的可比性,标准化处理后的法向量用D(d1,d2,d3)表示:
(2)
式中:norm为法向量D0的模;d01,d02,d03与d1,d2,d3分别为归一化处理前后的法向量D0和D在模型长、宽、高3个方向上的分量。

(3)
Fandisk为经典的复杂曲面结构模型,选取其作为实验对象介绍模型的分割过程不失一般性。基于网格法向量方向性原则可将Fandisk模型分为4组。图2(a)为网格法向量符合d2<0且d3>0的对应点云,顶面与4个相互独立且曲率变化一致的曲面连接为一个整体;图2(b)和图2(d)分别为侧视视角下网格法向量符合d2>0且d3>0、d2<0且d3<0的对应点云,前者包含的分割面彼此连接紧密且大部分区域未有明显的边界划分,而后者包含的4个分割面彼此独立;图2(c)包含模型中的底面与所有立面结构,网格法向量符合d1=1或d1=-1或d3=-1。
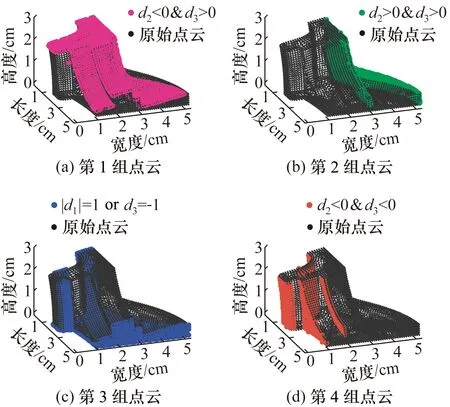
图2 Fandisk模型的4类分割面Fig.2 Four types of divided surfaces of the Fandisk model
2.2 多视角距离图像的生成
为了获取更完整的三维结构特征信息,引入六视图绘图概念,分别在主视、后视、左视、右视、俯视、仰视6个方向上将初次划分得到的各类点云转化为距离图像[9,10]。
以俯视方向为例,沿高度轴将此视角下包含的点竖直投影到长度轴与宽度轴所在的二维平面上,计算投影后各点之间的平均间距和点云扫描线之间的平均间距,将二者中的较大值作为网格边长。这样操作的目的是尽量保证划分后的格网中只包含1个激光脚点。利用格网化方法将映射到平面上的点进行划分,根据划分到网格内点沿映射方向的高程值对所在网格进行赋值。映射关系如图3(a)所示。当网格中仅包含1个点时,将该点的高程值赋值给该网格;当多个点同时被划入同一网格内时,该网格的高程值被指定为网格内所有映射点的距离均值;若未将点划入网格中,将所有映射点的最小值作为网格高程值。经过对所有网格进行赋值处理,生成俯视视角下的距离图像,如图3(b)所示,随着高程值的增加图像中灰度由深到浅变化。同理,按照上述规则可对其余5个视角下的点云数据进行相应处理生成六视角下的距离图像,此时图像中包含模型的全部特征信息。
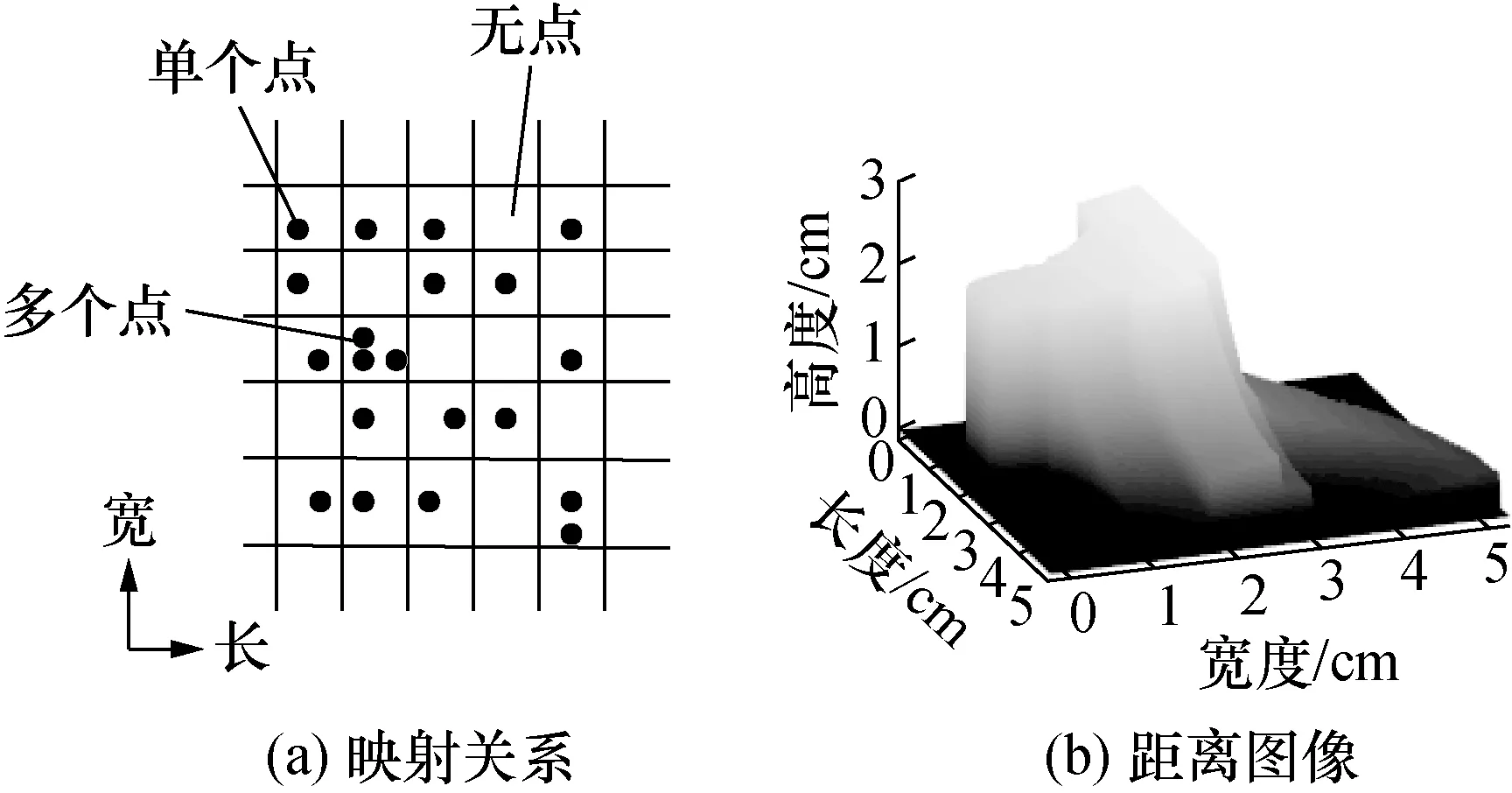
图3 俯视视角下的距离图像Fig.3 Distance image in vertical view
2.3 基于距离图像的种子点获取
距离图像以灰度的深浅变化来表征其高程变化,随着高度值的增加灰度由深及浅,且相邻面相较于同一面的灰度变化程度更为剧烈。利用Canny算子对灰度突变的敏锐性检测不同面的边缘信息。
由于原始模型中存在过渡边界变化不明显的部分区域,因此Canny算子检测得到各个区域的边缘信息可能存在断点和噪声。如图4(a)所示,在俯视视角下检测获取到第1组点云的原始边缘信息并不完整,在圆圈标注区域内均存在断裂情况。利用式(6)中闭运算算法填补图像中的空洞区域[11,12]:
[f⊕g](u,v)=max{f(u+x,v+y)+g(x,y)}
(4)
[fΘg](u,v)=min{f(u+x,v+y)-g(x,y)}
(5)
f·g=[(f⊕g)Θg]
(6)
式中:⊕为膨胀符号;Θ为腐蚀符号;·代表闭运算。
具体可分为两步进行:首先由式(4)对原始图像f(u,v)进行膨胀处理,运算过程可描述为在选定局部区域内计算原始图像与结构元素g(x,y)灰度值总和,将最大值替换原始灰度值;其次,利用式(5)对膨胀后的图像做腐蚀处理,使处理后的图像缩减细化。图4(b)为经过闭运算处理得到的各分割面边缘信息。此时断裂区域内各分割面边缘已经按照原始增长趋势紧密连接成为5个独立连通域;针对每一独立连通域,计算其重心坐标,依据距离图像与点云数据之间的映射关系,提取对应三维空间中的点,此点即为种子点。图5为依据上述步骤获取到顶面的种子点,此点位于该面的中心位置,用圆点表示;顶面边缘点用米字符号表示。
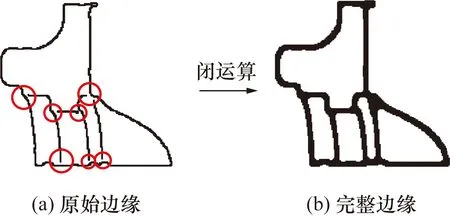
图4 待分割面边缘提取Fig.4 Edge extraction of awaiting surfaces
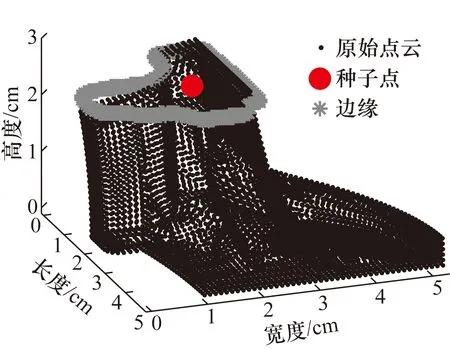
图5 种子点获取Fig.5 Acquisition of seed point
2.4 基于区域生长算法的面分割
基于上述处理获取待分割区域内的种子点,以种子点为生长中心,利用区域生长算法对各个面进行分割[13]。步骤为:搜索距离种子点最近的法向量,定义其为种子法向量;依据法向量是否平滑生长对邻接面进行分离,并在多个视角下进行细化分割,从而获取彼此独立的分割面;针对各独立面,以种子点为生长中心按照迭代搜索最近点的原则提取各点,并利用KNN算法的距离度量剔除离群点完成模型的优化分割。流程见图6所示。
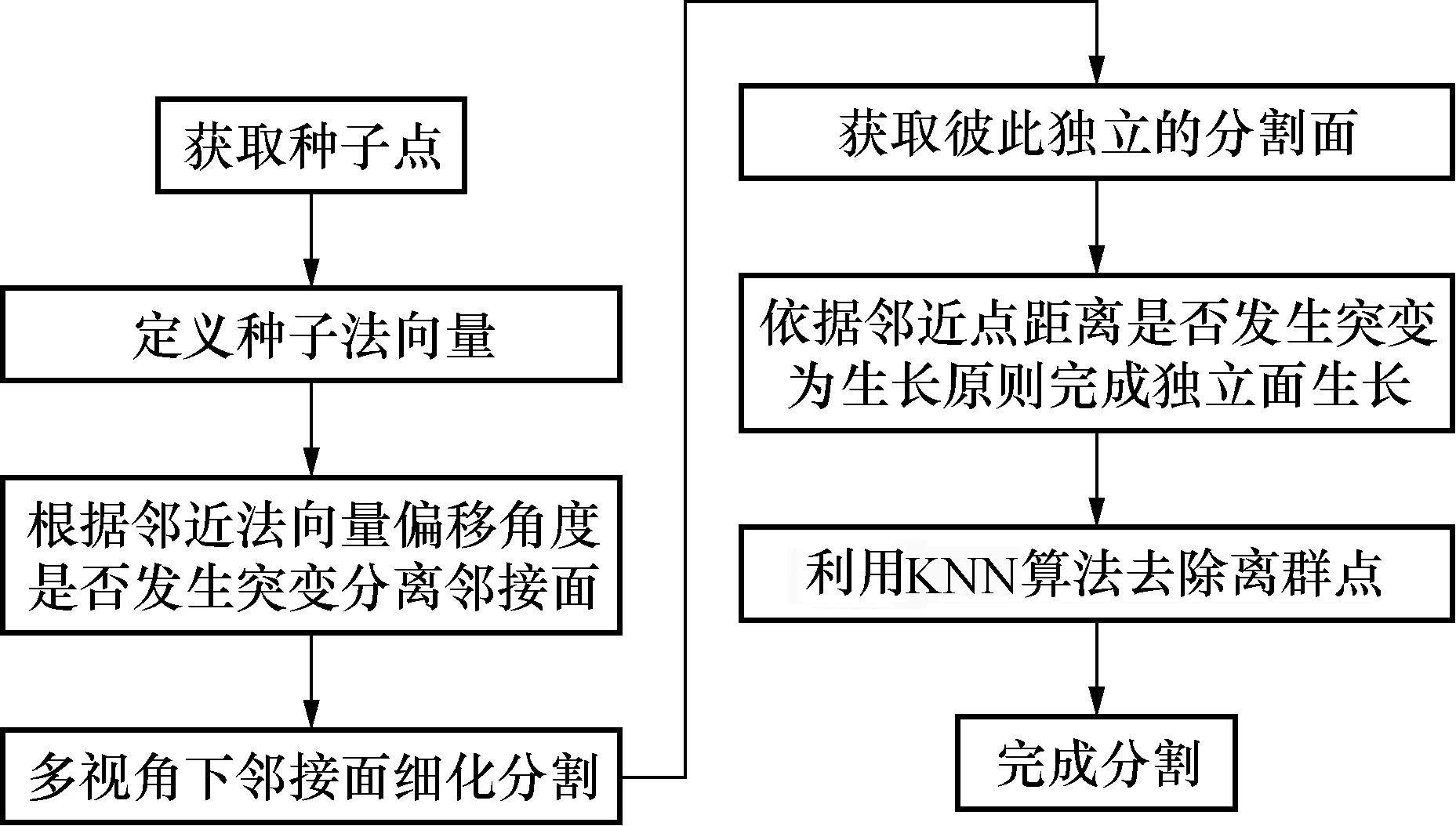
图6 区域生长算法流程图Fig.6 Flow chart of region growing algorithm
2.4.1 邻接面分离
引入网格法向量的偏移角度作为邻接面之间的差异性度量,将每组点云均分割成独立面结构。以第1组点云为例,构建此类点云的网格结构并求解各三角面片的重心坐标,将距离种子点最近的网格重心点定义为网格种子点[14],其所在三角面片的法向量定义为种子法向量Vs(vcx,vcy,vcz),网格法向量用Vg(vxi,vyi,vzi)(i=1,2,3,…,k)表示,k为此类待分割区域中所有参与运算的网格法向量数量;在种子法向量的邻域内搜索距离最近的法向量并利用式(7)计算其与种子法向量的偏移量cosβ,依据式(8)将所得偏移量数值转化为弧度制表征的角度Ang。
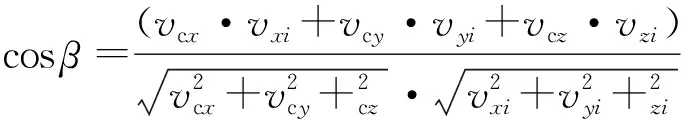
(7)
Ang=acos(cosβ)
(8)
若最近邻域法向量与种子法向量的偏移角度Ang变化微小,其表征相邻法向量生长平滑,即对应的点云未生长到邻接面上,此时更新此法向量为种子法向量,将其在原始法向量点集中剔除;若偏移角度Ang变化数倍以上,则判定该法向量与原始法向量处于异面,即点云已生长到邻接面上[15],此时原种子法向量维持不变,并将此法向量视为噪点予以剔除。
按照上述判定规则循环遍历集合中的所有法向量获取归属于同一分割面的全部法向量,进而提取组建对应网格的点得到目标区域的分割结果,如图7所示,即为顶面与其余独立面的分离结果。在多个视角重复上述操作,可将邻接区域细化分割成多个独立的分割面。

图7 邻接面分离Fig.7 Separation of adjacent surfaces
2.4.2 独立面提取
将点的距离度量作为各个独立面的生长准则实现各面的划分[16]。计算待分割区域内各点之间的距离均值,将此数值作为距离阈值K。以种子点作为生长中心,搜索距离此点的最近点,计算两点之间的距离值并与距离阈值相比较,若此距离值与距离阈值数值相近,则此点包含在目标分割区域内,更新此点为新的种子点并重复上述操作;反之,若两点间的距离值相较于距离阈值有一个突变,则此点已超出目标分割面区域,停止生长。提取结果如图8(a)所示,在4个曲率变化一致且相互独立的点云集中,将其中1个面完整地提取出来。
2.4.3 基于KNN的离群点去除
如图8(a)所示,经过上述处理获取到的目标分割面可能存在异常点,因此需要对其进行离群点检测。对于1个完整的分割面,面内任意一点均包含完整的四邻域和八邻域[17],在边界处也至少保证周围包含3个点。基于KNN算法搜索目标分割面中各点邻域内的最近3个点,并按距离值升序排序;若最远距离值远大于面中各点的平均距离阈值K,则此点视为离群点,将其在分割面数据集中剔除;剔除后的离群点归入剩余待分割面的数据集中,继续按照区域生长规则完成其余各面的分割。如图8(b)所示,经过上述处理后目标分割面中已经基本不存在具有明显特征差异的异常点。
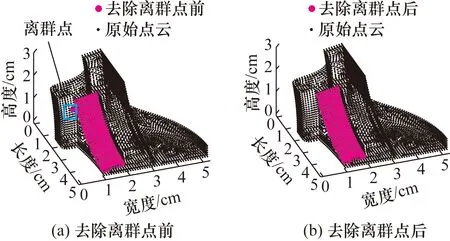
图8 离群点去除Fig.8 Deletion of off-group points
3 实验结果与分析
电脑配置为:CPU Intel Core i5 3.20 GHz,内存12 G。开发环境为Matlab,选取Fandisk、Block、Candle 3个复杂点云模型,在同一实验环境下,分别应用混合流形谱聚类算法[18]、顶点聚类算法[19]和本文算法进行分割实验。分割结果见图9。
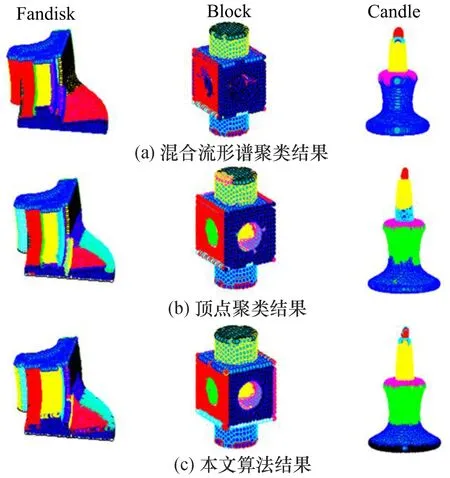
图9 分割结果对比Fig.9 Comparison of segmentation results
混合流形谱聚类算法采用混合概率主成份分析(MPPCA)法获取点的几何特征并构建邻接矩阵,在谱聚类空间中利用N-cut将点云特征信息融入低维向量,借助类间类内划分(BWP)算法实现模型无监督分割。如图9(a)所示,采用此类方法可对模型各部分进行有效分割,但对边界特征模糊和邻接面区域分割效果欠佳,易将多个区域划分为同一自由曲面。如Fandisk模型的两侧区域、Block模型的中空区域及Candle模型中间部分均有较大面积出现过分割与欠分割现象。
顶点聚类算法依据曲率、法向量以及顶点位置构造多维空间描述模型的局部表面特征,并将student-t混合模型(SMM)应用于模型三维网格结构进行顶点聚类,从而实现模型各部分的合理分割。由于输入的特征约束较多,因此该类算法对模型划分过于精细,可能将归属于同一面的区域多次划分。如图9(b)所示,Block模型的顶面和Candle模型上半部分中近似圆柱的区域在各自模型中本应属于同一区域,但均被分割成两部分。
结合图9(c)中本文算法的分割结果可知,相较于前两种算法,本文所提出算法对3种模型分割效果更为完整,无明显区域的错误分割。不仅对立面与曲面有良好的分割效果,对于特征模糊区域同样可以准确识别。
3种算法的分割精度Rac[20]为:
(9)
式中:Sp为理论上标准分割区域所包含点的个数;Tp为实际的分割数据点个数;|Sp-Tp|为错误分割的数据点个数。
表1为各算法的分割精度对比。混合流形谱聚类算法对结构较为复杂且特征模糊区域的模型分割效果欠佳,整体分割精度较低,分割精度在55.84%~83.38%之间;顶点聚类算法在所选取的模型上分割效果较稳定,分割精度不低于80%;本文算法对Fandisk和Candle的分割精度均高于90%,由于Block模型整体点云数据过于稀疏,应用3种算法得到的分割精度均偏低,但应用本文算法的分割精度仍高于其余2种方法。
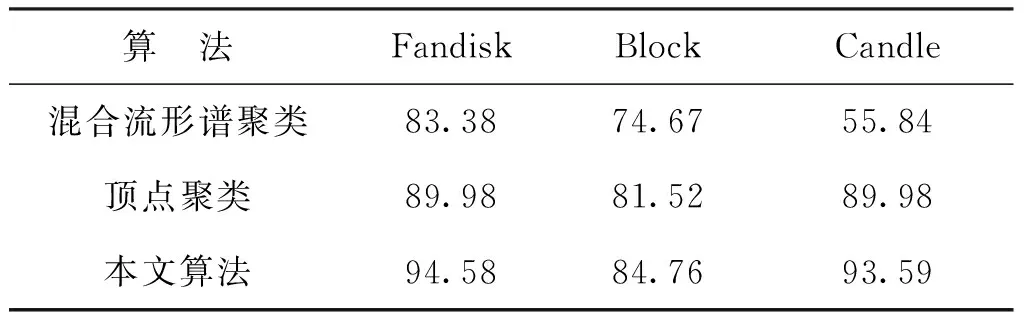
表1 各算法分割精度Tab.1 Segmentation accuracy of algorithms (%)
4 结 论
根据复杂点云模型的特征,提出了一种基于多视角区域生长的复杂点云模型分割方法。借助多视角距离图像对传统区域生长算法加以改进,以距离图像所对应点云区域内的重心作为种子点,保证种子点选取的稳定性;以网格法向量偏移角度和各点之间的距离度量作为生长约束条件改善生长过程中的过分割与欠分割现象。在选取的数据集上与其余2种分割方法进行测试比较,实验结果表明,本文算法相较于其余2种分割方法对特征模糊区域识别效果更佳,可获得不低于80%的合理分割结果。

