不同AB线型嵌段共聚物分子对自组装结构周期影响的研究

赵 斌，胡珺玥

（台州学院 电子与信息工程学院，浙江 台州 318000）

0 引言

嵌段共聚物是由小分子通过共价键连接而形成的一类高分子聚合物，由于不同分子之间相互排斥，所以会发生相分离；同时由于共价键连接的限制，相分离形成的热力学稳定态结构的大小通常在5～100 nm的介观尺寸之间。虽然AB型嵌段共聚物可以自组装形成一系列的纳米尺寸结构，如层状相结构（lamella，L）、两种双连续结构（gyroid，G；Fddd，O70）、六角柱状结构（cylinder，C），以及球状相结构（body center cubic，BCC），但是背后的物理机制目前已经比较清晰，即熵跟焓竞争的结果（F=U-TS）[1-6]。以简单的AB两嵌段共聚物为例，当A嵌段的体积分数fA为0.5时，AB两嵌段共聚物自组装形成稳定的层状结构，此时界面能（焓）最小（U较小），而熵的损失比较大（S较小）。随着A嵌段的体积分数fA的减少，B嵌段的体积分数fB的增加,自组装形成的稳定结构就会产生从层状相到双连续结构、柱状相、球状相，最终到无序相的转变，在此过程中熵的损失逐渐减少（S变大），同时焓的损失逐渐增加（U变大）。对于不同的AB型嵌段共聚物，自组装形成的结构相图都比较类似，不同的地方仅是相边界有一定的移动[7]。但是最近的研究发现，在嵌段共聚物自组装的过程中除了简单的熵与焓的竞争之外，其他物理参量也有很重要的影响。例如，穿孔层状结构（perforated lamellae，PL）作为另外的双连续结构，稳定性不如gyroid双连续结构，这是因为穿孔层状结构的截面曲率变化太大，导致堆积受挫，熵的损失较大，因此如何制备稳定的穿孔层状结构是一个很有意义的研究课题[8]。为了增加嵌段共聚物自组装形成的结构的种类，通常会有改变外场以及改变分子的结构两种方式来丰富其自组装形成的稳定态结构[9-12]。例如，将AB两嵌段共聚物受限在Rg尺度（Rg指在聚合物的回转半径）下的柱中，可以自组装形成类似于DNA的双螺旋结构；将AB两嵌段共聚物进行分叉处理获得杂臂型的ABn两嵌段共聚物，由于AB嵌段之间存在构象不对称，使A嵌段所形成的球状相区扩大，同时球状结构的相畴也随之变大，进而可以获得稳定的Frank-Kasperσ复杂球状相结构；在A1BA2三嵌段共聚物之外聚合一段B均聚物，获得A1B1A2B2四嵌段共聚物，在A/B总体积分数相等的条件下合理地调控各嵌段的体积分数同时控制相应的分离强度，可以获得稳定的层球混杂结构（Lamella-Sphere,LS）,其中较长的A1嵌段自组装形成层状结构，而较短的A2嵌段形成球状结构。由AB型嵌段共聚物自组装形成的混杂结构不仅丰富了软物质自组装的相系列，而且进一步加深了对嵌段共聚物自组装机理的认识，增加了自组装有序纳米结构在工业中应用的可能性。

由于嵌段共聚物自组装形成的结构可以用于光子晶体[13]、生物载药[14]以及污水处理[15]等各个领域，因此嵌段共聚物自组装形成的热力学稳定态受到科学界的广泛关注。例如，2019年美国得克萨斯大学奥斯汀分校的研究人员发现，通过设计ABC三组分嵌段共聚物自组装，获得的层状结构（lamella，L）、双连续结构（gyroid，G），以及六角柱结构（cylinder，C）可以对水的流动性产生不同的影响，进而有可能作为纳米尺寸的净水器件。在工业上，制备间距小于10 nm的有序柱状排列作为新一代的量子信息器件，也是个非常热门的领域，国内外的一些课题组都取得了很好的结果，其中美国的明尼苏达大学更是设计出了1.2 nm尺寸大小的层状相结构[16]。目前普遍认为，要获得小尺寸的热力学稳定态结构，通常是通过增加嵌段间的分离强度以及减小链段的数目来实现的。但是现实的高分子聚合物材料之间的分离强度不会一直增加，因此我们需要设计一种更好的方案来减小嵌段共聚物自组装结构的尺寸大小。

本文提出一种通过改变嵌段共聚物分子嵌段分布的方案，在保持所有可控参数不变的条件下，将AB分子剪切成A1BA2分子以及A1B1A2B2分子，来计算对形成层状结构以及柱状结构周期的影响。计算结果表明，通过将AB分子剪切为A1BA2分子以及A1B1A2B2分子，相应分子自组装形成结构的尺寸也会降低，进而验证了我们的设计思路。

1 理论方法

2 结果与讨论

文中的三种分子的结构，如图1所示。为了计算AB分子的链段分布对自组装结构周期的影响，首先计算AB、A1BA2和A1B1A2B2三种分子形成层状周期的链段分布、周期大小以及可能的链段构型分布图，如图 2 所示。在计算中设定：（1）对 A1BA2分子，fA1=fA2；（2）对 A1B1A2B2分子，fA1=fA2，fB1=fB2。

图1 不同AB线型分子的链段示意图

从在图2（a）可以看出，随着分子的嵌段数的增加，链段分布也将变得更加复杂。其中，如果A1与A2聚集在相同的A相畴中，则形成“looping（环形）”结构；如果A1与A2聚集在不同的A相畴中,则形成“bridging（桥连）”构型，不同的嵌段构型分布导致层状相结构的周期大小也随之改变；在多嵌段共聚物中，为了减小熵的损失，更容易形成“looping（环形）”构型。显然，形成“looping（环形）”构型与形成“bridging（桥连）”构型时的周期会减小。在图2（b）中，通过计算不同周期下的层状相结构的自由能，来确定相应参数下自由能的极小值以及相应的周期大小。显然，为了节省计算资源，会寻找自由能极小值对应的结构最小周期。在图2（c）中，通过计算AB分子的链段分布随分离强度（χN）的变化规律，可以发现，随着分离强度的增加，链段将被进一步拉伸，界面链段的浓度变化也会逐渐变陡，因此相应的层状结构周期尺寸也会增加（在固定分离强度的条件下，链段右侧的坐标减左侧坐标，就是对应的周期大小）。在图2（d）中，通过计算不同分子结构的周期随分离强度（χN）的变化，可以发现，随着分子嵌段数的增加，分子形成“looping（环形）”构型的可能性就会增加，因此相应分子形成的层状相周期尺寸也会相应降低，即相同的参数下，A1B1A2B2分子形成的层状结构周期最小，而AB分子形成层状结构周期最大。

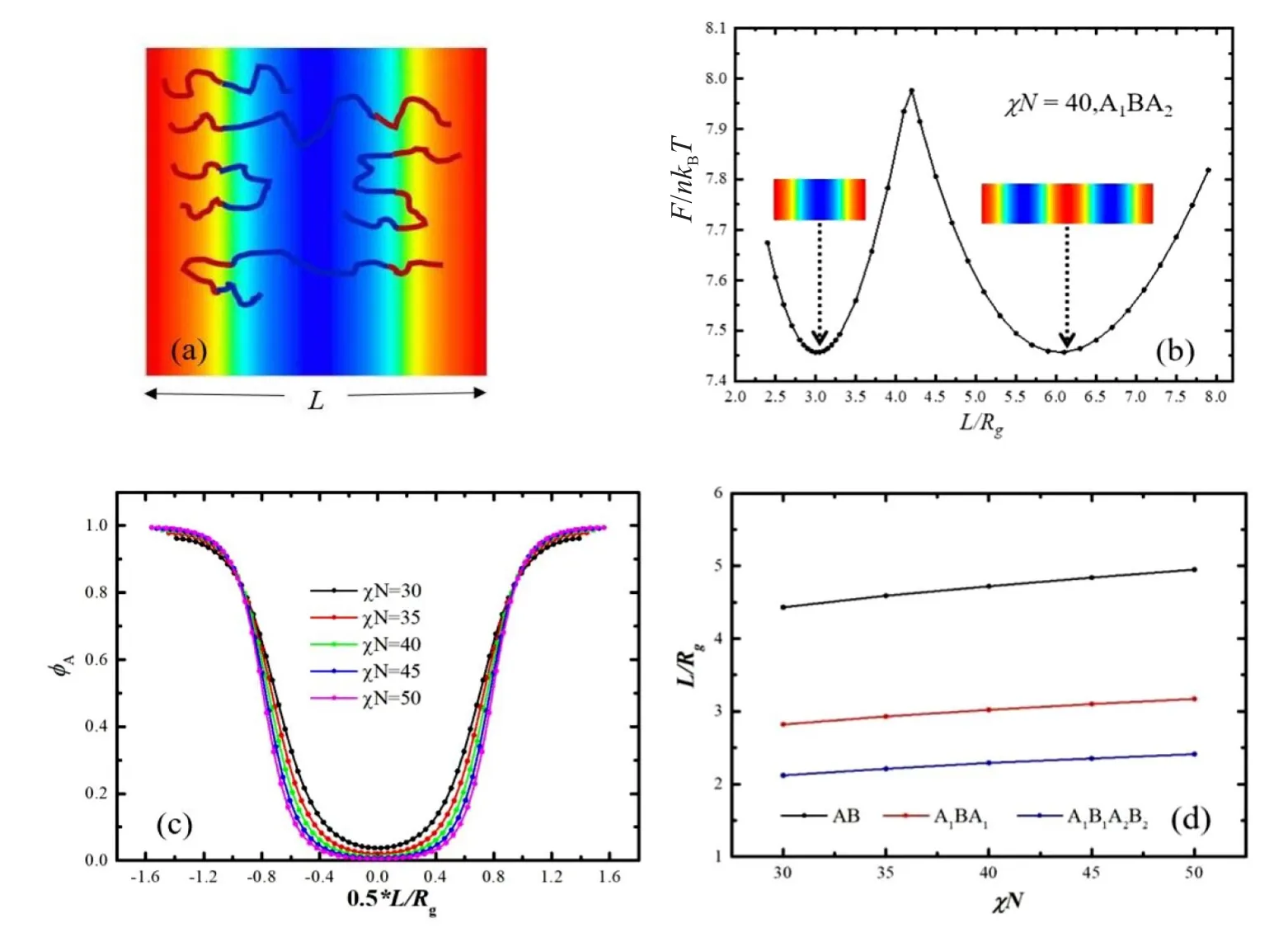
图2 不同分子形成层状周期的链段分布情况

为了证明AB分子的链段数对自组装形成的有序结构的周期具有普适影响，我们进一步计算了AB、A1BA2和A1B1A2B2三种分子形成柱状周期的链段分布以及周期大小，计算中固定fA=0.75，fB=0.25，如图3所示。

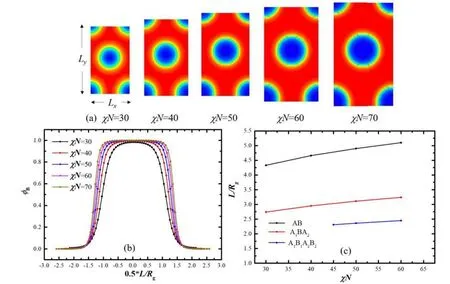
图3 不同分子形成柱状周期的链段分布情况

从图3（a）和图3（b）可以看出，AB分子形成的柱状相结构的周期随分离强度的增加而增加，说明增加分离强度（χN）使得链段的拉伸更加剧烈。从图3（c）可以看出，随着分子嵌段数的增加，分子形成“looping（环形）”构型的可能性也会随之增加，相应分子形成的柱状相周期也会相应降低。因此，在类似的参数调控下，柱状相周期的变化规律与层状相的周期变化规律一致，即A1B1A2B2分子形成的柱状结构周期最小，而AB分子形成柱状结构周期最大。

3 结论

通过以上计算，可以得出，在AB线型嵌段共聚物中，AB分子的嵌段数会对自组装形成的结构周期产生很大的影响。在固定AB分子结构的条件下，随着分离强度的增加，自组装形成的层以及柱状结构的周期会在焓的作用下增加；而在固定分离强度的条件下，随着AB分子嵌段数的增加，自组装形成的层以及柱状结构周期会在熵的作用下而减小。因此，可以通过增加AB分子的嵌段数，获得更小尺度的自组装结构，以期为制备更小尺寸的纳米器件提供理论指导。