广义协变Hamilton系统的应用
王 根
(厦门大学 数学与科学学院,福建 厦门 361005)
1 广义结构Poisson括号与广义协变Hamilton系统
其中,结构矩阵Jij(x)=-Jji(x),广义Hamilton系统的表达式为
定义1[6]r上两个函数f,g∈C∞(M,)的广义结构Poisson括号
{f,g}={f,g}GPB+G(s,f,g),
其中,G(s,f,g)=-G(s,g,f)∈C∞(M,)为几何括号,并且它的表达式为
G(s,f,g)=f{s,g}GPB-g{s,f}GPB.
几何括号的引进对于推广后的广义Poisson括号是必须的, 它成功地将流形结构与函数的动力学演化连接了起来, 极大地扩大了研究的范围.因此,完整的广义结构Poisson括号可以写为
{f,g}={f,g}GPB+f{s,g}GPB-g{s,f}GPB.
显然,通过在流形上引入一个几何标量函数,一个结构函数或势函数s∈Ck(M),它是一个由相应的流形空间决定的实值光滑函数.注意,s∈Ck(M)中的势函数s只表示流形本身的属性.换句话说,它的具体公式由流形给出.这将适用于许多环境.
很显然,根据广义结构Poisson括号立刻就可以给出广义协变Hamilton系统的表达式.
定理1[6]根据广义结构Poisson括号,则有
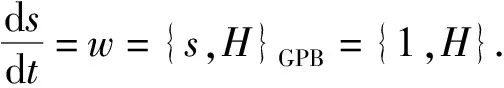
定理2[6]流形上典则完备Hamilton方程与典则协变Hamilton方程分别为
式中{·,·}={·,·}GPB+G(s,·,·)为广义结构Poisson括号,Di=∂i+Ai为广义导数算子.
正则协变哈密顿方程,由广义协变哈密顿系统关于xk和pk给出,可以精确地写成
式中,bk=JjkAj, 以及Ak=∂ks为结构导数,对于坐标与动量的完整广义Hamilton系统分别为
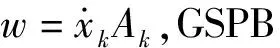
{xj,pk}=δjk+xjAk-pkbj.
2 V-测地线方程
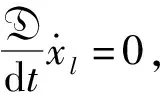
对于V-测地线方程,代入S-动力学系统,很显然,我们可以得到
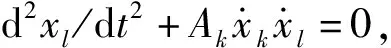
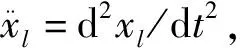
3 算例

这是广义Hamilton系统理论描述的.
下面我们考虑广义协变Hamilton系统.首先考虑完整的广义Hamilton系统,

式中,Ak=∂ks.此时的S-动力学系统经过计算表达式为
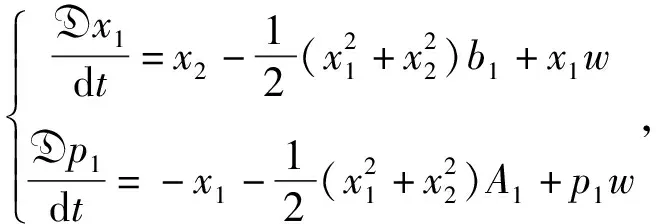
4 展望
研究广义协变 Hamilton系统已经取得了一些成果,由于它本身就是描述非线性系统,这一点可以从V-测地线方程看出,对于广义协变Hamilton系统的许多细节还有待于进一步研究,例如广义协变Hamilton系统的对称性问题等.

