简化反应堆一回路系统自然循环的动态比例特性研究

李向宾，詹奔腾，王忠毅，李浩永

(1.华北电力大学，北京 102206；2.非能动核能安全技术北京市重点实验室，北京 102206；3.国家电投集团科学技术研究院有限公司，北京 102209)

自然循环作为关键非能动技术之一，已广泛应用于先进反应堆的非能动系统。如事故工况时非能动堆芯冷却系统可通过自然循环及时排出堆芯余热，从而保证反应堆的安全。通常情况下，对应的自然循环均处于瞬态过程。鉴于瞬态过程的复杂性，有必要通过试验深入了解其动态特性。限于规模和经济性，大部分试验均是基于缩比试验台架进行的，故必须进行比例分析来保证模型试验对原型现象的可复现性[1]。如AP600/AP1000/CAP1400系列核电站非能动系统的性能验证即基于APEX、SPES、ROSA和ACME等4个缩比实验台架的实验结果而定[2-5]。而数十年来，关于自然循环的比例分析方法也得到了较充分的发展。Ishii等[6]研究得到了基于一维守恒方程的单相和两相自然循环的比例准则；赵冬建等[7-8]在一维漂移流模型的基础上导出了两相自然循环相似准则；卢冬华等[9-10]分析得到了1组统一的适用于单相和两相自然循环系统的无量纲准则数组。这些方法作为经典H2TS(双向分层比例分析)方法的进一步发展[11]，已被应用于相关自然循环系统的缩比设计。但以前的研究并没有基于上述方法对自然循环瞬态过程关键参数的变化特性进行评价。Reyes[12]提出了一种动态比例分析(DSS)理论，将守恒方程的积分形式变换为相空间坐标内的形式，并通过二参数的仿射变换得到对应的比例缩放方法，以此来研究动态的比例进程。文献[13]将此理论发展应用于简单矩形环路内单相自然循环瞬态进程的比例分析，但并没有应用于反应堆系统。

本文基于简化反应堆一回路系统，在实验验证的基础上，利用H2TS和DSS方法对其自然循环现象进行比例分析，同时使用RELAP5程序计算不同比例尺度下升降功率时的自然循环瞬态过程[14]，并将两种方法下的计算结果进行对比分析，评估对应工况下关键参数的动态变化规律。

1 比例分析

之前的研究已详细给出了简单矩形环路内单相自然循环的相似准则数[13]。为简化起见，本文仅列出相关的修改部分。首先，基于H2TS方法下的自然循环相似准则数为：

(1)

(2)

(3)

其中：∏Ri为表征浮力和惯性力之比的理查森数；β为流体热膨胀系数；g为重力加速度；H为冷热段中心位置高度差；ΔT0为冷热段稳态温差；u0为稳态流动速度；∏Fri为摩擦数；f为摩擦系数；l为循环通道长度；d为管道直径；k为局部损失系数；∏Qs为热源数；q为加热段热流密度；ρ为流体密度；cp为流体比定压热容。为保证模型和原型现象相似，对应的相似准则数应相等，即模型和原型准则数的比值∏R=∏m/∏p=1。一般情况下，摩擦数可通过调整环路内的阻力系数而得到满足，故可暂不考虑。考虑到堆芯实际结构参数，上述热源数可修订为：

(4)

其中：ζ0为加热周长；ai,0为截面积。

设模型和原型的堆芯组件结构相同，即管径和栅距保持不变[9]，则有：

a0,R=ζ0,R

(5)

在等物性条件下，由式(1)和(5)可得H2TS方法下对应的相似准则，即：

(6)

本研究中，在缩比实验台架的堆芯模拟体内，应用1个燃料组件模拟体作为热源，对应原型电厂157个燃料组件，由式(5)可得管道的直径比dR=0.138 3。则等物性条件下的相似准则可归纳为：

(7)

文献[13]中已详细推导了简单矩形环路内基于DSS方法下的单相自然循环相似准则。为便于同H2TS进行对比，仍设定不对摩擦数进行相似分析(仅由系统调整保证)，且取dR=0.138 3，则等物性条件下基于DSS方法所得的相似准则为：

dR=0.138 3，u0,R=lR，qR=lR

(8)

对比两种方法下的相似准则可知，若取同样的缩比尺寸，则采用两种方法所得的缩比模型几何结构完全相同，而速度比和热流密度比则明显不同。显然，采用DSS方法所需的模型热流密度明显小于基于H2TS方法所得的对应数值，这与文献[13]结论一致，也是DSS方法的一个明显特点。

2 数值模型验证

为保证计算的准确性，首先将已有的实验结果与基于RELAP5程序计算所得的结果进行对比。

2.1 模型

图1为用于测试反应堆一回路系统自然循环现象的全压自然循环实验台架(FITY)简化示意图[15]。此台架是以压水堆为原型、H2TS方法为理论指导得到的实验装置(长度比例为1∶4)，主要包括1个堆芯模拟体(含有1个与原型反应堆系统完全相同的燃料组件)、1个蒸汽发生器、1个稳压器及相关管路和阀门。实验时，堆芯模拟体和蒸汽发生器分别作为热源和冷源，即可形成自然循环。为利用RELAP5程序进行计算，首先基于此实验台架建模并进行组件划分，节点示意图如图2所示。其中，108管道组件代表作为热源的堆芯模拟体，116和204管道组件分别代表蒸汽发生器传热管的管侧和壳侧，环路压力通过波动管304由稳压器302控制，泵组件121在自然循环期间仅提供阻力。内置于二次侧水箱中的216和217管道组件作为二次侧传热管，用于排出系统热量。计算所采用的边界条件和初始条件均依据实验数据设置。

图1 自然循环实验台架示意图Fig.1 Natural circulation test facility scheme

图2 数值模型节点示意图Fig.2 FITY nodalization scheme

2.2 验证

1) 节点敏感性分析

为评估不同节点数对计算结果的影响，以加热段108组件为例，分别计算不同节点数时其出口的稳态温度，如图3所示。可看出，108组件的温度变化范围随节点数的增加而减小，且当节点数到达8以上后，其趋势已明显变缓。因此，综合考虑计算时间和计算精度，加热段的节点数选为11，其他各组件的节点数也做类似处理。

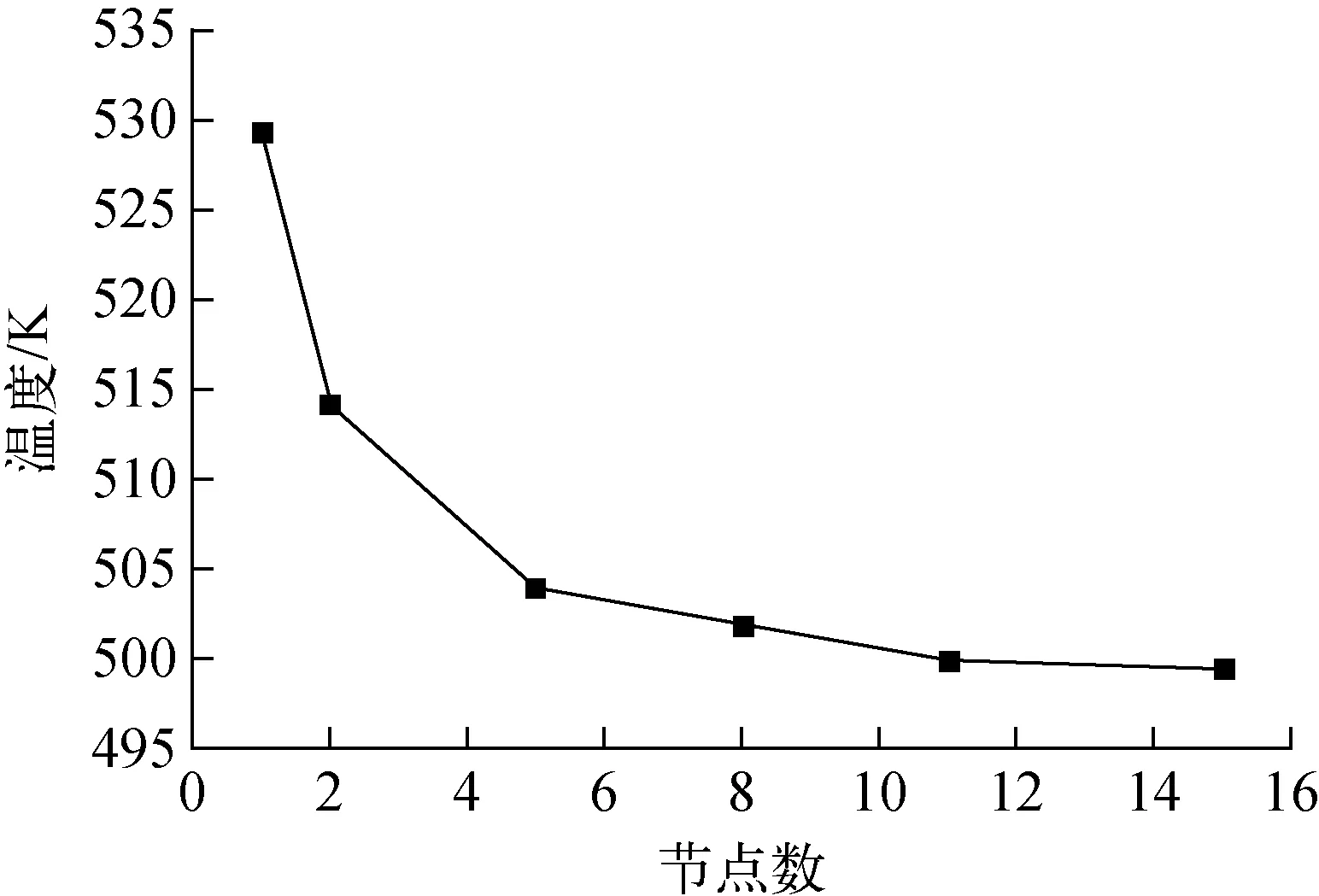
图3 108段出口温度随节点数的变化Fig.3 Temperature at 108 exit under different node numbers

2) 稳态结果分析

首先，分别采用实验和数值计算获得5种不同加热功率(136、149.5、167.9、183.2、218.0 kW)下环路内的稳态自然循环流量，结果如图4所示。其中，EXP和RELAP分别代表实验结果和数值计算结果。可见，环路流量均随加热功率而增大，数值计算结果与实验结果基本一致，两者间的最大误差约为3%。在单相自然循环情况下，其他工作压力下的流量对比结果以及冷热段温差计算结果的偏差均与此类似，说明数值计算结果可较好地反映实验现象。

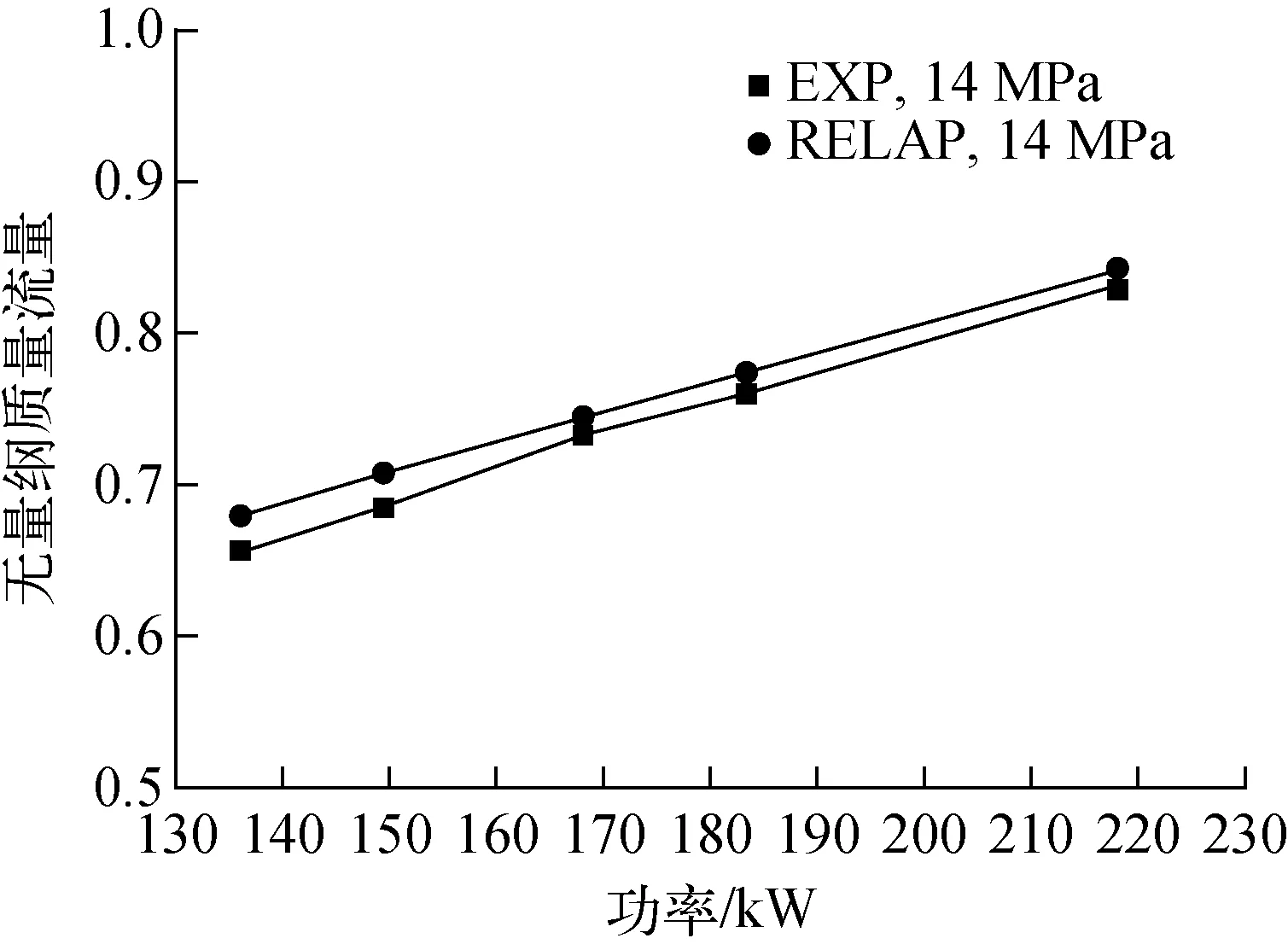
图4 无量纲质量流量随加热功率的变化Fig.4 Dimensionless mass flow rate under different heating powers

3) 瞬态结果分析

表1列出了包括4种阶跃升功率工况和3种阶跃降功率工况下的功率设置。对于每一种工况，首先在初始功率下达到稳态，之后再按照设定的功率变化速度进行功率调整，直至达到最终设定功率，并趋于稳态。本文中，选择不同的功率变化速度是为了评估功率变化速度对环路自然循环的影响。功率阶跃变化的最大值约为初始功率的5%。

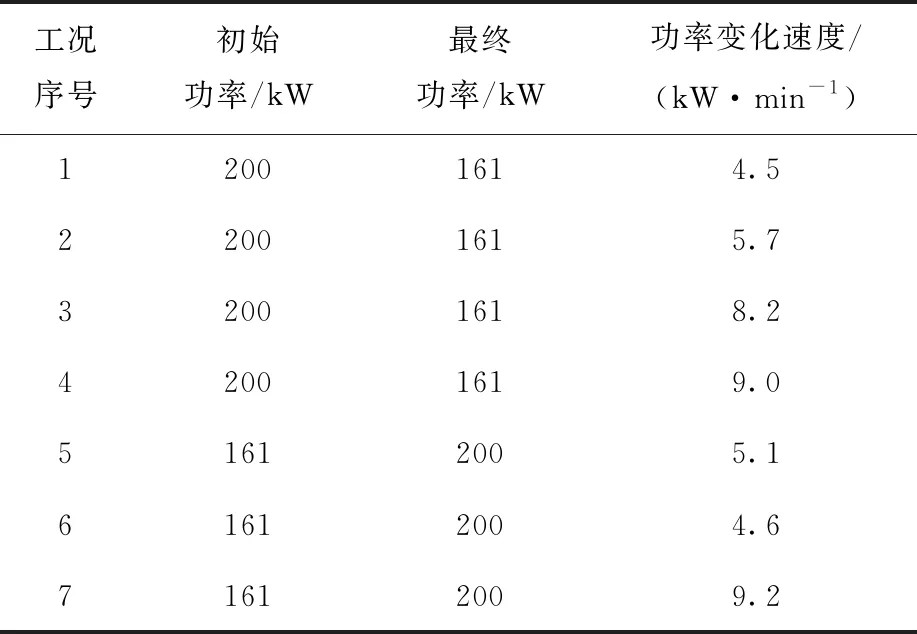
表1 瞬态工况下的功率设置Table 1 Power setting under transient condition

图5为降功率和升功率情况下的瞬态质量流量分布。其中，EXP-x和RELAP-x分别代表x工况下的实验结果和数值计算结果。

由图5a可看出，在所有工况下，流量的变化速度都直接受到加热功率变化速度的影响。功率下降得越快，流量到达稳定所需的时间越短，但流量波动幅度越大。相对于功率以初始值3%左右的速度阶跃下降的工况(对应工况1和2)，功率以初始值5%左右速度阶跃下降时(对应工况3和4)的流量变化快得多。500 s之前，实验值的波动幅度明显高于计算值。这是因为数值计算仅基于沿流动方向的一维流动而获得，而且所采用的时间步长可更小，因此质量流量变化相对平稳，而实际实验测量则受采集频率等多种因素的影响，故波动幅度较大。稳态时实验值和计算值的总体偏差约为7%，且计算值的下降幅度更小。这是因为目前所测数据是一回路的流量，而实验时二回路对一回路的冷却也同样基于一个非能动系统完成。稳态时，一回路加热功率和二回路冷却系统处于平衡状态；功率下降时，二回路系统自然循环的响应相对延缓，在此过程中带走的热量偏多，所以平衡时一回路维持在低流量水平(同理，升功率时一回路维持在高流量水平，图5b)。而数值模拟时对二回路系统做了部分简化处理，导致响应加快。

从图5b可知，各工况的实验值和计算值的偏差及对应变化特征与降功率工况下的情况基本类似。需要指出的是，工况7下的流量峰值，包括实验值和计算值，均明显高于最终的稳态值。这是由于工况7下功率阶跃变化速度较大(范围约为初始值的5.7%)。因此，以下计算中的功率阶跃变化范围限制为初始功率的5%，以避免过大的流量波动。总体上，RELAP5程序可较好地模拟瞬态自然循环。

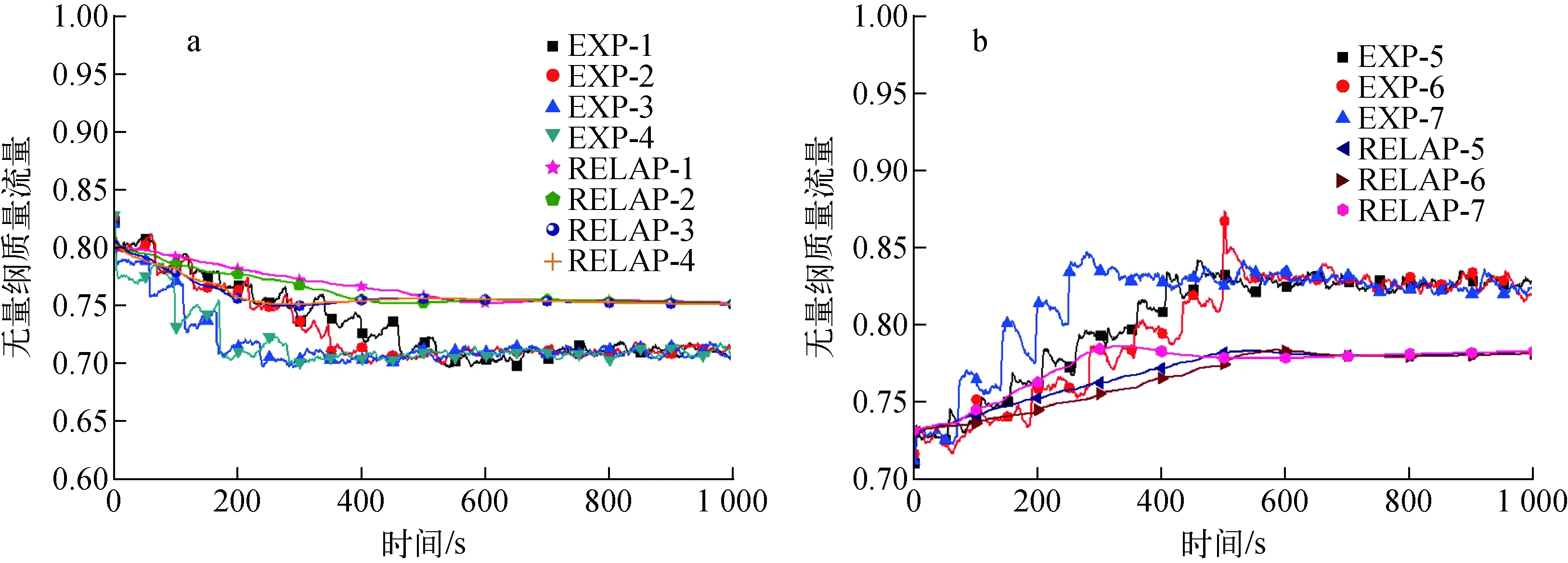
图5 降功率(a)和升功率(b)下的瞬态质量流量Fig.5 Mass flow rate under power-down case (a) and power-up case (b)

3 比例特性分析

基于一典型的长度比例lR=0.25来分析瞬态自然循环的比例特性。表2为分别基于H2TS方法和DSS方法所得的比例数。可看到，在相同的几何尺度下，基于DSS方法可得到更小的缩比功率。利用RELAP5程序分别计算了降功率工况和升功率工况下的自然循环，并将结果进行了对比。

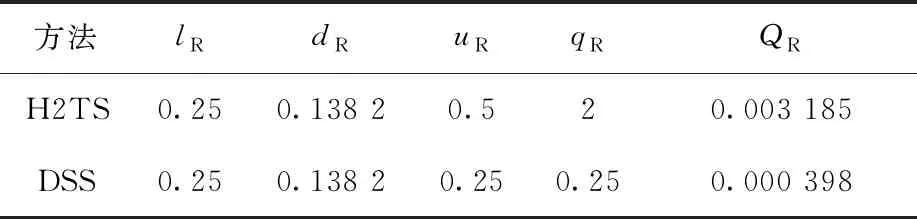
表2 基于H2TS方法和DSS方法所得的比例数Table 2 Scaling number based on H2TS and DSS methods

3.1 降功率工况结果分析

本文模拟了4种降功率工况，功率变化均采用阶跃下降形式，具体参数列于表3。

表3 降功率工况下的功率设置Table 3 Power setting under power-down case

图6为所有工况下的流量变化，其中H2TS-x和DSS-x分别为基于两种比例方法所得缩比模型不同工况下的计算结果，t*=t/t0为参考时间，t0为不同比例方法下系统功率改变后下一个稳态循环周期所需的时间。为便于对比，根据对应工况下时间比例的要求对t0进行了比例调整。可见，两种方法下所得的质量流量变化趋势均与原型结果类似，即流量在初始阶段较短时间内迅速变大，之后在经历一段时间的波动后，又开始逐渐增大。总体来看，基于H2TS方法计算所得的流量到达稳态值的时间稍长，而基于DSS方法计算得出的流量更接近于原型结果。另外，两种方法下4种工况所得的流量曲线都分别重合，这说明5%阶跃功率范围内不同的功率变化速度对自然循环的瞬态流量变化没有明显影响。

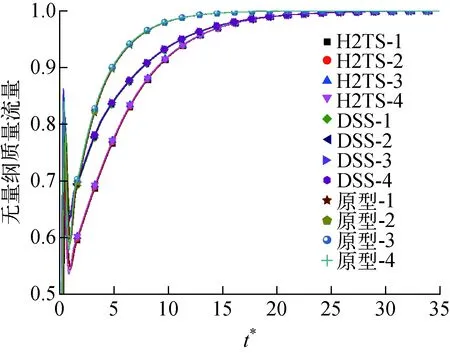
图6 工况1～4下的瞬态质量流量对比Fig.6 Transient mass flow rate under case 1-4

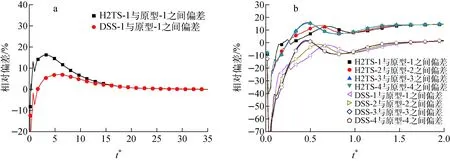
a——长循环周期；b——前两个循环周期图7 不同循环周期内的质量流量相对偏差Fig.7 Relative error of mass flow rate in different cycles

图8为工况1下基于冷段和热段出口温度计算得到的温差曲线及对应的相对偏差。由图8a可看出，初始阶段冷热段温差的波动幅度大于流量波动幅度，这是因为功率突变时首先会造成温度的变化。对比流量变化曲线可知，基于H2TS方法所得的温差曲线更接近于原型。由图8b可见，温差偏差变化趋势与流量偏差类似，但基于DSS方法所得偏差较大。

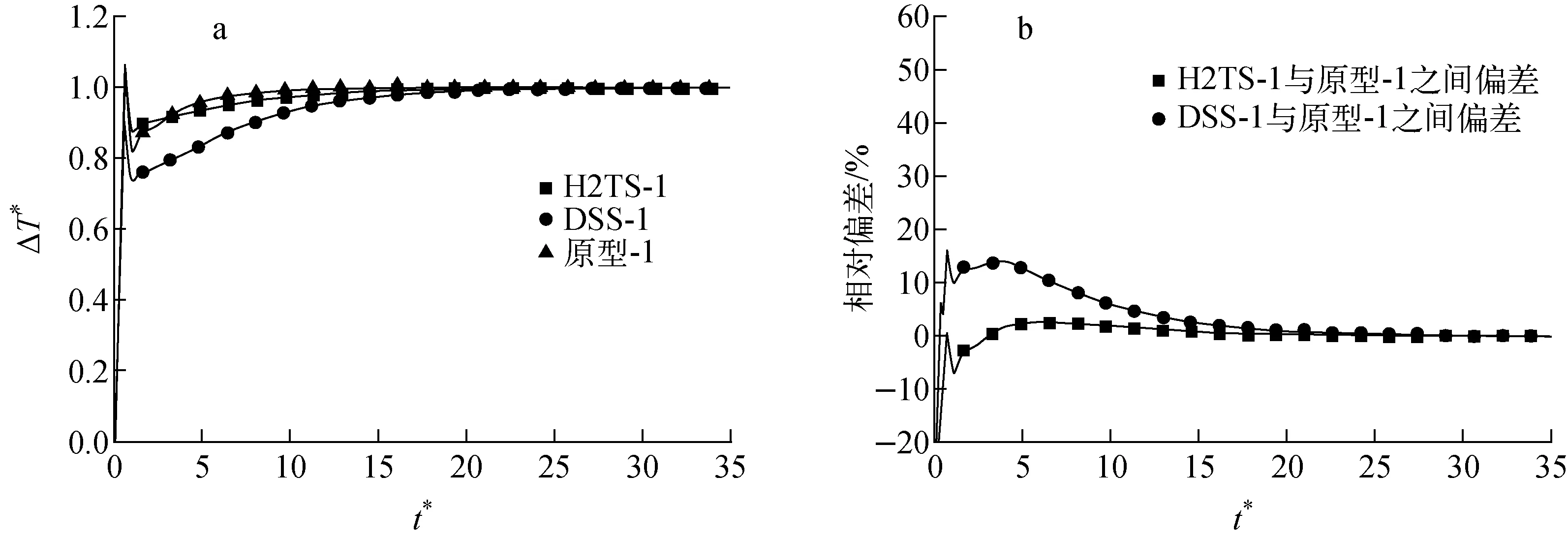
图8 工况1下的瞬态温差(a)及其偏差(b)分布Fig.8 Transient temperature difference (a) and its relative error (b) under case 1

3.2 升功率工况结果分析

为便于对比，计算了基于3种不同功率变化速度的升功率工况下的自然循环，功率变化仍设置为阶跃形式(表4)。图9为工况5下的流量曲线及对应的偏差曲线，其他工况下的变化与此类似。对比降功率工况可知，基于H2TS方法所得流量更接近原型工况数值，而初始阶段基于DSS方法的偏差明显大于基于H2TS方法的偏差。图10为前两个循环周期内所有升功率工况下的流量偏差，其总体变化趋势与降功率工况类似。图11为工况5下的温差曲线，所有曲线都有较高的重合度，对应的总体偏差都非常小，均在5%范围内。

表4 升功率工况下的功率设置Table 4 Power setting under power-up case

图9 工况5下的瞬态质量流量及其偏差Fig.9 Transient mass flow rate and its relative error under case 5

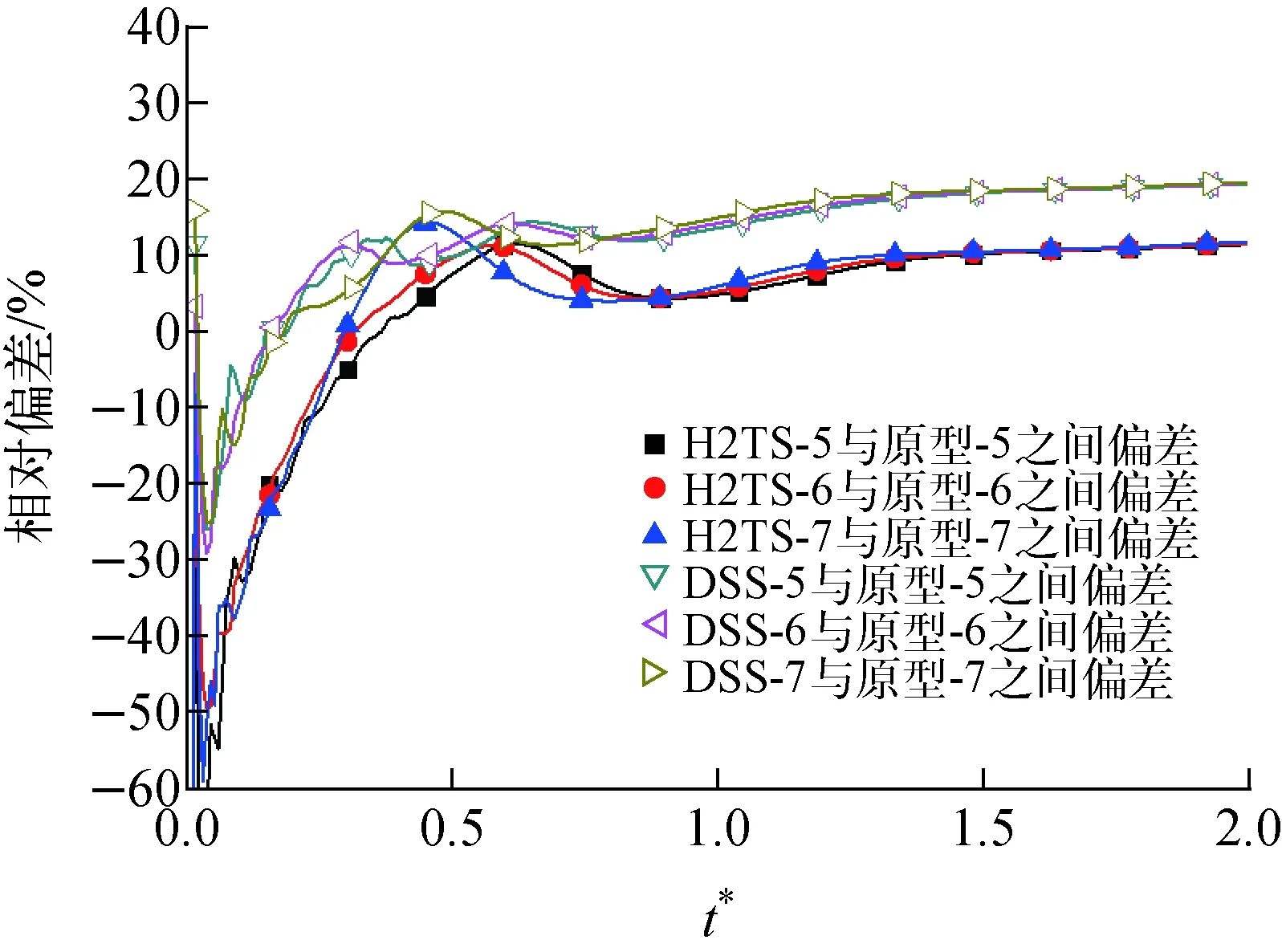
图10 前两个周期内的质量流量偏差Fig.10 Relative error of mass flow rate in the first two cycles

图11 工况5下的瞬态温差分布Fig.11 Transient temperature difference under case 5

4 结论

针对简化反应堆一回路系统的自然循环，分别采用H2TS方法和DSS方法进行了比例分析，并在实验验证的基础上，模拟了降功率工况和升功率工况下自然循环的瞬态过程，分析了自然循环流量等关键参数的动态变化，得到如下结论：

1) 基于RELAP5的数值计算结果与实验结果基本一致，5%初始功率内的阶跃功率变化不会引起过大的流量波动；

2) 基于两种比例分析方法所得缩比模型下的计算结果均可反映原型参数变化，流量和温差的整体失真度均小于20%；

3) 所有工况下，自然循环流量和温差在初始阶段0.5个循环周期内存在较大的波动，之后则相对平稳。

本文仅针对简化反应堆一回路系统内瞬态自然循环的关键参数变化规律进行了对比分析。关于不同比例分析方法下相似准则数的动态失真度评价以及各类参数变化的不确定性分析，包括升降功率工况下流量失真度的不同变化特点，将在后续研究中进一步探讨。