高温氢工质热物理性质计算分析

房玉良，王成龙，田文喜，苏光辉，秋穗正

(1.西安交通大学 能源与动力工程学院 动力工程多相流国家重点实验室，陕西 西安 710049； 2.西安交通大学 核科学与技术学院 陕西省先进核能技术重点实验室，陕西 西安 710049)

氢元素是最简单、最轻的化学元素，也是宇宙中最多的元素，氢原子由1个质子和1个核外电子组成。作为一种绿色清洁能源，氢工质主要用作燃料、火箭推进剂、冷却剂和化工原料等，在未来能源系统转型、宇航推进动力中将具有广阔的发展前景。

氢分子H2是一种分子量很小的双原子分子，摩尔质量为2.015 88 g/mol。氢分子存在两种自旋异构体，即两个核自旋平行的正氢(Ortho-hydrogen，O-H2)和两个核自旋反平行的仲氢(Para-hydrogen，P-H2)，两者物理性质有所差异，化学性质相同，可相互转化。热平衡状态下的氢气称为标准氢(Normal hydrogen，N-H2)，在室温时，N-H2中的P-H2与O-H2之比为3∶1。N-H2的三相点为13.957 K，沸点为20.369 K，临界压力为1.296 4 MPa，临界温度为33.145 K，临界密度为31.262 kg/m3，偏心因子为-0.219。

基于氢工质在航天动力推进、基础物理学、等离子体物理学等方面的应用，研究人员开展了宽温度、压力范围内的氢工质热力学性质与输运性质的基础研究[1-9]。相关实验研究和理论分析为物性计算程序开发积累了可靠数据、计算模型支持。早期程序[10-14]开发主要基于Fortran语言，采用数据表格插值或物性计算模型求解方法，通过输入压力、温度(或比焓)获取氢工质液态、气态、热解平衡态等条件下的密度、比焓(或温度)、比熵、声速、比热容、比热容比、黏度、导热系数等相关热物性参数。这些程序的计算范围从三相点到104K、101～109Pa不等。美国国家标准局总结了20世纪80年代之前氢的热物性研究，发布了两本重要专著[15-16]，部分成果被当作科研与工业应用领域的标准数据库。进入21世纪以来，氢的热物性研究进入了精细化、精确化阶段[17-18]，程序用户界面更加友好、编程环境与接口更加多样，使用方便快捷，如CoolProp、REFPROP等。

现有相关物性计算软件主要存在年代久远、模型与数据未及时更新，部分程序仅能计算分子氢物性等问题。本文基于最新的热物性模型，开展了高温氢工质热物理性质计算模型研究和程序开发，计算求解密度、比焓、比热容、声速、黏度、导热系数等热物性参数，可为氢相关行业科研及应用提供借鉴支持。

1 热物性计算模型

1.1 分子氢热物性

1.1.1状态方程 分子氢气作为实际气体考虑，状态方程采用Aungier-Redlich-Kwong (ARK)模型[19]：

(1)

(2)

n=0.498 6+1.173 5ω+0.475 4ω2

(3)

(4)

(5)

(6)

式中：p为压力，Pa；T为温度，K；V为比容，m3·kg-1；Rg为氢气气体常数，Rg=4 124.5 J·kg-1·K-1；b、c为常数，m3·kg-1；α0、α为系数；ω为偏心因子，-0.219；下标cr表示临界状态。

1.1.2比焓 比焓h采用实际气体状态方程可推导如下：

h=h0(T)+pV-RgT-

(7)

理想气体比焓h0(T)计算模型[2]如下：

(8)

式中，ai为系数。

1.1.3比定压热容 比定压热容cp采用实际气体状态方程可推导如下：

(9)

(10)

式中：ui、vi为系数；下标p表示定压。

比定容热容cV为：

(11)

式中，下标T、V分别表示定温、定容。

1.1.4声速 声速Csound计算如下：

(12)

式中：ρ为密度，kg·m-3；下标s表示定熵。

1.1.5黏度 黏度μ计算采用Muzny模型[4]：

(13)

(14)

(15)

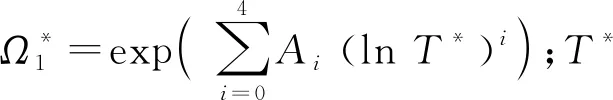
1.1.6导热系数 导热系数λ计算采用Assael模型[3]：

λ(ρ,T)=λo(T)+Δλe(ρ,T)+Δλcr(ρ,T)

(16)

(17)

(18)

(19)

式中，f1,i、f2,i、g1,i、g2,i、E1～E3为系数。

1.1.7扩散系数 扩散系数D计算模型[20]如下：

(20)

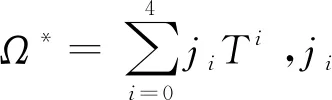
1.2 原子氢热物性

原子氢是一种由氢原子组成的亚稳态物质，在高温条件下视为理想气体。氢原子的摩尔质量为1.007 947 g/mol，原子氢气体热力学行为简单，只有空间3个方向上的平移，没有旋转和振动。

1.2.1状态方程 状态方程采用理想气体模型：

pV=RgT

(21)

式中，Rg为原子氢气体常数，Rg=8 248.9 J·kg-1·K-1。

1.2.2比焓 比焓计算模型[21]如下：

(22)

式中：k1～k5为系数；M为摩尔质量，M=1.007 947 g·mol-1；Tre为参考温度，Tre=T/1 000，K。

1.2.3比定压热容 比定压热容计算模型[21]如下：

(23)

1.2.4声速 声速计算如下：

(24)

式中，κ为绝热指数，κ=5/3。

1.2.5黏度 黏度计算模型[20]如下：

(25)

1.2.6导热系数 导热系数计算模型[20]如下：

(26)

1.2.7扩散系数 扩散系数计算模型[20]如下：

(27)

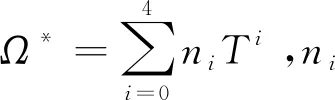
1.3 氢气热解及混合氢工质热物性

1.3.1分子氢热解 高温状态下，氢分子之间的共价键断裂形成两个氢原子，发生热解或热离反应。当温度足够高时，气体还会发生电离，电子脱离原子核束缚产生等离子体。在高温条件下，氢工质热解产生单原子氢与分子氢会使得热物理性质变化显著[1]。常压状态下， H2的热解温度约为1 500 K，在温度达到5 000 K以上时，H2几乎全部热解变成原子氢气体，如图1所示。分子氢热解过程如下：

图1 氢工质相图Fig.1 Phase diagram of hydrogen

(28)

(29)

平衡常数只与温度相关，与压强、物质浓度无关。本文采用H2热解平衡常数模型[5]为：

lgKp=-2.379 43×104/T+6.331 53

(30)

值得注意的是，T≤1 000 K时Kp≪10-10，因此本研究认为T≤1 000 K时的Kp=0。

由上述研究可知，原子氢的份额是温度和压力的函数，该模型计算结果与文献[5-6]数据对比如图2所示，两者相对偏差在±3%以内。

图2 平衡态下原子氢的份额对比Fig.2 Comparison of atomic hydrogen fraction in equilibrium state

1.3.2密度 密度采用质量分数加权计算：

ρH-H2=wH·ρH(T,p)+(1-wH)·ρH2(T,p)

(31)

式中：wH为原子氢质量分数；下标H-H2表示混合氢工质。

1.3.3比焓、比热容、声速 比焓、比热容、声速加权计算方式[6]如下：

hH-H2=α·hH(T,p)+(1-α)·hH2(T,p)

(32)

MH-H2·cp,H-H2=α·MH·cp,H(T,p)+

(33)

(34)

ΔH(T)=2MH·hH(T)-MH·hH2(T,1 bar)

(35)

MH-H2=xHMH+(1-xH)MH2

(36)

式中：α为热解度；ΔH为标准摩尔生成焓，即1 mol H2在标准状态下(压力为0.1 MPa)反应生成2 mol H产生的反应焓变；γ为绝热指数，γH-H2=wHγH+(1-wH)γH2，γH=5/3，γH2=cp,H2/cV,H2；R为通用气体常数。

1.3.4黏度 黏度计算采用文献[7-8]中的模型：

(37)

(38)

(39)

(40)

1.3.5导热系数 导热系数计算采用文献[7-8]中的模型：

λH-H2=λf+λr

(41)

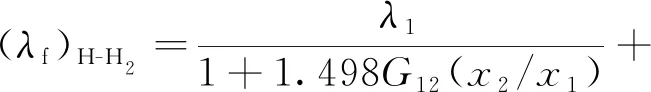
(42)

(43)

(44)

(45)

(46)

2 程序开发

公开文献调研到的相关氢工质热物性参数计算程序列于表1，这些程序的计算范围从三相点到104K、101～109Pa不等。

表1 氢工质热物性计算程序Table 1 Thermophysical property code of hydrogen

基于上述计算模型，本研究采用MATLAB程序开发平台编制了氢工质热物性参数计算程序Prop_H_H2。Prop_H_H2可计算100～3 500 K、104～5×107Pa范围内的H、H2及H-H2混合氢工质的密度、比焓、比热容、声速、黏度、导热系数、扩散系数等热物性参数。

2.1 程序组成与功能

Prop_H_H2为模块化结构设计，可作为其他程序的子程序。Prop_H_H2由输入模块、H热物性计算模块、H2热物性计算模块、H-H2热物性计算模块、热解模块、输出模块组成，各热物性计算模块内设置相应的热物性参数子函数。Prop_H_H2计算速度快，可实现单状态点计算，也可实现曲线计算结果输出，具有良好的人机交互绘图、数据储存、编程接口等特点。

2.2 程序计算流程

Prop_H_H2计算流程如图3所示，根据物质种类(H、H2、H-H2)、所需计算的热物性参数代码，通过输入温度、压力从而计算所选物质的相关物性参数。

图3 Prop_H_H2程序框图Fig.3 Block diagram of Prop_H_H2 program

3 计算结果与验证

3.1 H2热物性验证

本文采用REFPROP程序计算结果进行H2物性验证。REFPROP是由美国国家标准与技术研究院研制开发的工质热力学和输运性质计算软件，该程序提供包括MATLAB在内的多种编程接口。REFPROP计算N-H2热物性参数范围为13.957～1 000 K、约2 000 MPa，但无法计算热解平衡态的氢工质热物性参数。本文通过REFPROP计算模型外推获取1 000～3 500 K范围内的N-H2热物性参数。

Prop_H_H2与REFPROP热物性参数计算结果对比如图4所示，两程序计算结果符合较好。热物性参数相对偏差计算公式为：

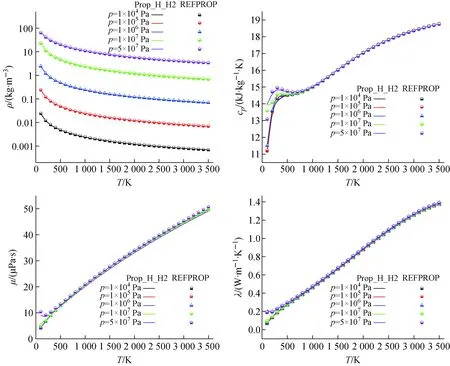
图4 H2热物性对比Fig.4 Comparison of H2 thermophysical property

(47)

式中，X代表相应的热物性参数。

图5示出H2热物性计算的相对偏差。结果表明：密度、比定压热容的最大相对偏差分别为6.80%、6.76%；黏度、导热系数的最大相对偏差分别为13.05%、13.21%。出现最大相对偏差的状态区域是在低温、高压区(100～200 K，1×107～5×107Pa)，此区域Prop_H_H2计算结果偏高。这是由于温度越低、压力越高，H2状态越靠近液相，本文中采用的ARK模型在该区域适用性相对较差，计算出的密度偏高，进而导致其他热物性在该区域处计算结果偏高。在200～3 500 K、1×104～2×107Pa范围内，Prop_H_H2与REFRPROP热物性参数计算结果的相对偏差在±1%以内。

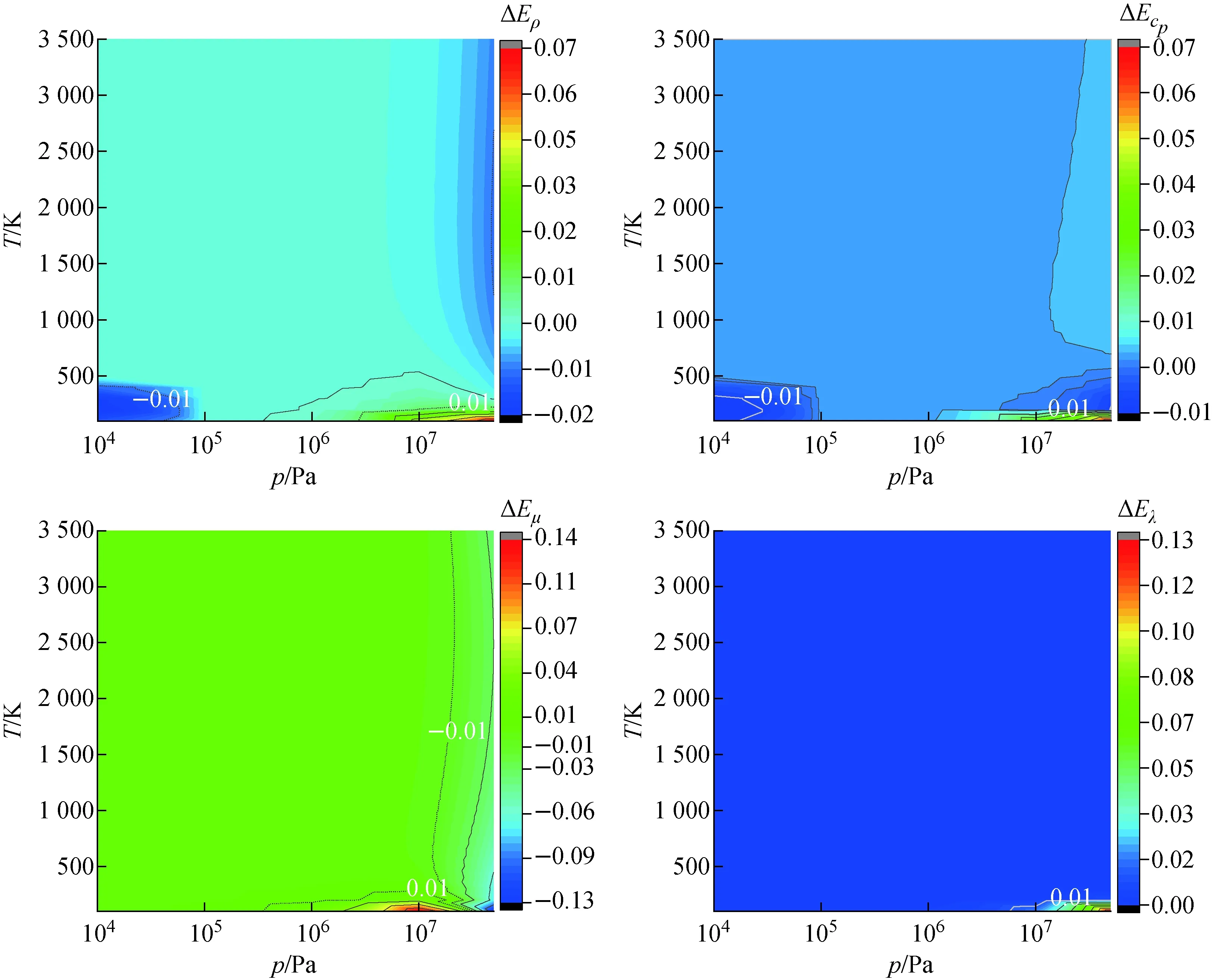
图5 H2热物性计算偏差Fig.5 Deviation of H2 thermophysical property

3.2 H-H2热物性验证

有关热解氢热物性的研究主要集中在21世纪之前，相关研究资料与数据相对有限。本文根据搜集到的文献数据[5-6，8-9，15，24]与Prop_H_H2计算结果进行验证对比。这些文献数据主要为20世纪90年代之前的数据，由美国国家标准与技术研究院、宇航局、洛斯阿拉莫斯国家实验室等机构提供，部分热物性参数与现有研究结果存在一定偏差。H-H2热物性参数对比结果如图6所示。由图6可见，Prop_H_H2计算的热解氢工质H-H2热物性参数偏高，偏差较大的区域主要集中在程序计算范围的边界区域，如高温、低压区和低温、高压区。

图6 H-H2热物性对比Fig.6 Comparison of H-H2 thermophysical property

在计算范围的大部分区域内，Prop_H_H2计算结果与文献值相差较小，相对偏差在±5%之内。Prop_H_H2在计算比热容、导热系数的过程中，考虑了分子氢热解过程中反应热的影响。因此，在热解反应程度较大，即原子氢摩尔份额占比较大时，比热容、导热系数随温度的变化有较大的波峰出现，图中发现其峰值出现位置在原子氢热解摩尔份额占比为50%附近。

综上，Prop_H_H2计算H2、H、H-H2的密度、比定压热容、黏度、导热系数等热物性参数在100～3 500 K、104～5×107Pa范围内是合理可靠的，计算值较其他程序、文献的结果偏高，最大相对偏差为±15%；在200～3 000 K、104～107Pa范围内，Prop_H_H2计算值会更加准确，相对偏差在±5%左右。

4 总结

本文开展了高温氢工质热力学与输运性质研究，建立了原子态氢、分子态氢、热解平衡态氢的热物性计算模型，并基于MATLAB语言开发了热物性计算程序Prop_H_H2。Prop_H_H2可适用于计算100～3 500 K、104～5×107Pa范围内的H、H2及H-H2混合氢工质的密度、比用性相对较差，计算出的密度偏高，进而导致其他热物性在该区域处计算结果偏高。在200～3 500 K、1×104～2×107Pa范围内，Prop_H_H2与REFRPROP热物性参数计算结果的相对偏差在±1%以内。

本程序可为氢工质相关的航天推进、物理学、能源动力等行业的科研和应用提供支持借鉴。