基于任意三角形网格的中子扩散变分节块法
尚 文,庄 坤,2,*,李 婷,汤晓斌,2,于东森
(1.南京航空航天大学 材料科学与技术学院,江苏 南京 211106;2.南京航空航天大学 空间核技术应用与辐射防护工业和信息化部重点实验室,江苏 南京 211106)
变分节块法(VNM)无需使用横向积分技术即可将节块的体积通量矩和偏中子流矩扩展为正交基函数之和,是核反应堆堆芯中子学计算最成功的节块法之一,由西北大学和阿贡国家实验室(ANL)首次提出,用于求解多群稳态中子扩散和输运方程。20世纪90年代中期,ANL开发的VARIANT是第一个基于VNM的程序[1],它被用于ANL(如REBUS代码)[2]和欧洲(如ERANOS代码)[3-5]的快堆设计。2007年,ANL又开发了名为NODAL的VARIANT程序新版本,作为UNC软件包中的求解器之一[6-7]。2011年,爱达荷州国家实验室(INL)的INSTANT程序也采用了变分节块法[8]。1995年,在DIF3D代码中增加了VARIANT用以提高快堆的通量解[9]。2014年,西安交通大学的李云召等开发了适用于三维矩形几何的反应堆堆芯计算程序VIOLET[10],后被用于压水堆堆芯计算的Bamboo-Core代码[11-13]的中子扩散模块。此外,VIOLET代码得到扩展以求解六角形几何的中子输运方程,被用作快堆计算代码系统NECP-SARAX的解算装置[14]。2018年,Zhang等[15]提出了基于矩形网格的改进变分节块法来求解三维稳态多群中子输运方程;2019年又将积分法应用于具有六角形组件的反应堆,提出了基于六角形网格的改进变分节块法[16]。
有限元法和基于任意三角形网格的变分节块法均采用Galerkin变分技术、泛函概念和非结构网格。其不同之处在于:1) 有限元法一般采用小尺寸网格划分和低阶试验函数,而变分节块法可使用高阶(>4)多项式函数来展开任意三角形网格内的空间变量;2) 有限元法计算有限元节块的展开系数,通过传递有限元节块值实现耦合,变分节点法则利用三维高阶(>4)多项式函数直接展开任意三角形网格内的空间变量,通过扫描并利用节块网格界面上净中子流和中子通量的连续条件实现耦合;3) 对于变分节块法,可直接由节块内中子通量的展开系数计算节块的精细功率分布,而有限元法则需根据有限元节块的展开系数进一步计算。
目前大多数变分节块法基于六角形或矩形结构几何网格,然而随着核能与核技术的发展,新概念堆型被不断提出,这些新型反应堆的一个重要特点是其组件设计和堆芯布置不再采用单一常规的几何形状和堆芯结构,因此基于矩形和六角形几何的变分节块方法不能准确计算新型反应堆堆芯中子学。考虑到三角形网格对曲线或多角形边界有很好的拟合性,理论上可用来逼近任意几何形状。另外,采用三角形网格进行计算时,可进行局部的网格加密,从而提高计算结果的准确性和可靠性。因此,本文拟研究基于任意三角形网格的多群中子扩散变分节块法。首先,对计算区域进行三角形网格剖分,将任意三角形变换为正三角形;其次,建立泛函并利用正三角形内正交基函数展开节块内参量;再次,利用变分原理获得中子通量密度与节块边界上分中子流的响应关系;最后,基于传统源迭代法对其进行求解。基于上述理论模型开发程序TriVNM,并采用基准题验证程序TriVNM的可靠性与精确性,以及对具有复杂几何组件堆芯的适用性。
1 理论模型
首先,从多群中子扩散方程出发,有:
Σs,gΦg(r)+Sg
(1)
其中:g为能群编号;Φg(r)为中子标通量密度,cm-2·s-1;Dg为中子扩散系数,cm;Σt,g为中子宏观总截面,cm-1;Σs,g为群内宏观散射截面,cm-1;Sg为中子源项,cm-3·s-1,包括散射源项和裂变源项。
(2)
其中,g′为能群编号。
其次,利用Galerkin变分技术,对中子扩散方程在整个求解域上建立一个包含三角形节块中子平衡方程的泛函F:
(3)
其中,节块v的贡献为:
(4)
χγ=J·nγ
(5)

(6)
其中:nγ为边界γ的外法线方向向量;χγ为节块边界上沿外法线方向的净中子流密度。
再次,采用坐标变换将ANSYS软件对计算区域剖分的任意三角形节块变换为成正三角形节块,如图1所示。

图1 任意三角形坐标变换示意图Fig.1 Arbitrary trianglar coordinate transformation
任意三角形和正三角形的坐标转换关系为:
(7)
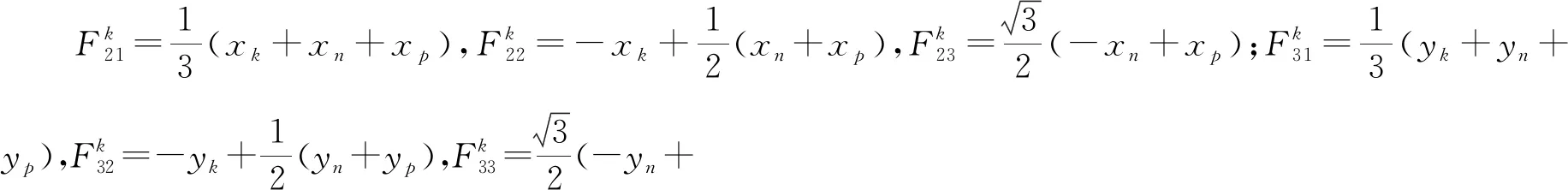
坐标变换后进行基函数的构造。线性无关的函数{1,x,y,z,x2,xy,xz,y2,…}构成函数向量g(r):
g(r)=[1,x,y,z,x2,…]T
(8)
显然,该函数系在积分区域内不是正交归一的。而正定对称矩阵G一定与单位矩阵相似,即存在满秩矩阵Q并满足下式:
(9)
QGQT=I
(10)
令f=Qg,满秩矩阵Q保证g(r)和G两组基函数所张成的函数空间相同,即:
span{f1,f2,…}=span{g1,g2,…}
(11)
(12)
矩阵Q可用Gram-Schmidt算法求解。通过上述坐标变换,即可构造出正交归一的基函数。
将式(4)中节块内中子标通量密度Φg(r)、中子源项Sg和节块边界上的净中子流密度χγ分别按照正三角形的基函数展开,其中,空间基函数fi和hkγ为完全的正交多项式。
(13)
(14)
于是,中子标通量密度和源项的展开式系数之间满足以下关系式:
(15)
将式(13)代入式(4),得到:
Fv[φ,χ]=φTAφ-2φTs+2φTMχ
(16)
其中:φ、s、χ为中子通量密度、中子源Sg和净中子流密度χγ的展开系数组成的向量。矩阵A和M的计算公式为:
Aij=(3Σtr)-1Pij+δijVvΣr
(17)
(18)
M=[M1M2…Mγ…]
(19)
(20)
分别令关于φT和χγ的一阶变分形式为0,可得:
φ=A-1s-A-1Mχ
(21)
(22)
Ψ=MTA-1s-MTA-1Mχ
(23)
为将响应矩阵表达成通用形式,定义边界上的分中子流密度为:
(24)
Ψ=2(j++j-)
(25)
χ=j+-j-
(26)
将式(25)、(26)代入式(24),得到离散后的中子扩散方程:
j+=Bs+Rj-
(27)
φ=Hs-C(j+-j-)
(28)
式中:j+和j-分别为节块边界上的出射流中子密度矩向量和入射流中子密度矩向量;B、C、H和R为响应矩阵。
最后,根据上述推导,得到变分节块法中的节块响应关系:
(29)
(Ij-RgП)jg=Bgsg
(30)
φg=Hgsg-Cg(Ij-Π)jg
(31)
式中:jg为节块的出射中子流密度向量(省去了上标“+”),cm-2·s-1;Bg、Cg、Hg和Rg为由几何与材料共同决定的响应矩阵;Ij为大小与分中子流密度向量相对应的单位矩阵;Π为节块分中子流密度之间的联系矩阵,包含了内部边界上相邻节块间的互为出入射关系和外边界上的边界条件。
将式(29)代入式(30)、(31),可得:
(32)
(33)
将所有能群合并,可得到算子形式的变分节块法:
(34)
(35)
Fgg′=χgνΣf,g′
(36)
所有三角形节块通过中子流相互耦合,然后利用传统的源迭代法对其进行求解。含特征值的裂变源问题采用幂法迭代求解,称为裂变源迭代。在每次裂变源迭代中,需在已知裂变源f的情况下,进行多群迭代。
2 数值结果
通过以上理论模型,本文基于FORTRAN90语言开发了基于任意三角形网格的变分节块法中子扩散计算程序TriVNM。分别采用2D/3D-IAEA、2D/3D-LRA、2D/3D-VVER440、2D/3D-VVER1000、不规则几何基准题验证程序TriVNM正确性。本文只选择矩形几何组件的2D-IAEA、六角形几何组件不带反射层的3D-VVER1000和非结构几何组件这3个具有代表性的基准题进行说明。以下所有计算均基于Intel(R) Core(TM) i7-7700 CPU@3.60 GHz。
2.1 2D-IAEA基准题
2D-IAEA基准问题[17]是一个简化的两群PWR基准问题,堆芯共有177盒燃料组件,组件的几何尺寸为20 cm×20 cm,堆芯1/8对称分布,堆芯布置和网格剖分如图2所示。堆芯按双区布料方案布置,径向有20 cm厚的水反射层,堆芯外边界条件为真空边界(即入射中子流密度为0),所有组件均采用等效均匀化的参数。由于此基准问题堆芯布置了控制棒,而且在堆芯和反射层交界面上,热中子通量梯度很大,因此广泛用于校核双群中子扩散方程的数值计算模型及其计算精度。

图2 2D-IAEA基准题1/4堆芯布置示意图(a)和网格剖分示意图(b)Fig.2 Configuration of 2D-IAEA benchmark (a) and its meshing by ANSYS code (b)
TriVNM计算的有效增殖因数keff为1.029 560 7,2D-IAEA基准题给出的keff参考值为1.029 585。可看出,与参考值相比,有效增殖因数的计算偏差仅为2.360 pcm。图3为用程序TriVNM计算的归一化功率分布及与参考值的比较,可看出,归一化功率的最大偏差出现在堆芯最内圈的组件上,约为0.20%。表1为TriVNM计算结果与其他程序计算结果的比较,可看出,TriVNM计算结果符合参考解且较其他程序的偏差小。

表1 2D-IAEA基准题在不同程序下的计算结果Table 1 Calculation results of 2D-IAEA benchmark problem with different programs

图3 归一化功率分布计算结果及与参考解的对比Fig.3 Calculation result of normalized power distribution and comparison with reference result
2.2 3D-VVER1000基准题
3D-VVER1000基准题是不带反射层的2D-VVER1000基准问题[17]的扩展,径向上有8圈燃料组件,全堆芯共有25根控制棒,堆芯布置呈1/6旋转对称,组件的对边距为23.6 cm。堆芯轴向高度为200 cm,25根控制棒中的6根提到堆芯中部。堆芯的径向外边界反照率为0.125,轴向反照率为0.15。TriVNM计算时,径向上将每个六角形节块划分为8个三角形,轴向上每10 cm划分为1层,参考解仍是由细网差分程序DIF3D-FD在径向上将每个六角形组件划分为384和486个三角形、轴向上每5.0 cm为1层的计算结果外推得到。
3D-VVER1000全堆芯计算耗时446.81 s,TriVNM计算的keff为1.011 240 9,3D-VVER1000基准题给出的keff参考值为1.011 350,与参考值相比,有效增殖因数的计算偏差仅为-10.788 pcm。图4为1/6堆芯示意图及TriVNM计算的归一化功率分布及与参考值的比较,归一化功率的最大相对偏差出现在最外圈组件上,约为0.344%。为验证程序的计算精度,对同类程序的计算结果进行对比,结果列于表2。可看出,与其他程序相比,程序TriVNM计算结果与参考解的偏差较小。
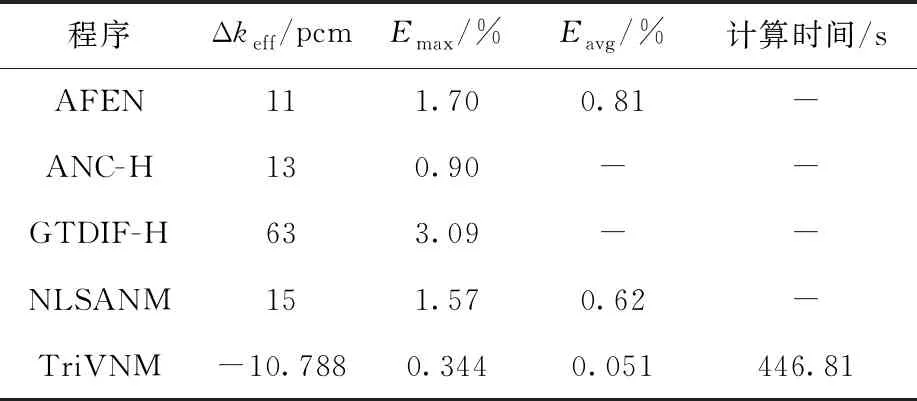
表2 3D-VVER1000基准题在不同程序下的计算结果Table 2 Calculation results of 3D-VVER-1000 benchmark problem with different programs

图4 归一化功率分布计算结果及与参考解的对比Fig.4 Calculation result of normalized power distribution and comparison with reference result
2.3 带无限大反射层的两区堆芯例题
为检验程序在不规则非结构几何下的计算准确性,选择文献[18]中的例题3进行计算。非结构几何组件堆芯布置如图5所示,两区堆芯位于无限大的水池中。堆芯分Ⅰ、Ⅱ两区排布,堆芯外围为反射层(即水池),取其半径为45 cm来代替无限大反射层。

图5 非结构几何组件堆芯布置Fig.5 Layout of irregular geometric assembly problem
基于三角形网格的程序TriVNM对复杂几何形状具有良好的适用性,因为三角形网格组合理论上可逼近任意几何形状。图6为网格剖分示意图,由TriVNM计算的归一化功率和keff以及其他程序的计算结果列于表3,其中FEM2D和ABFEM-T均基于有限元方法。相比之下,由TriVNM计算的keff偏差为20.1 pcm,且由TriVNM计算的keff和归一化功率均与其他程序较为吻合。验证了基于任意三角形网格的程序TriVNM适用于复杂几何堆芯。
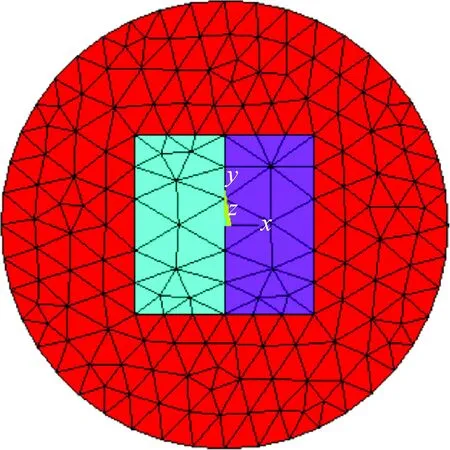
图6 非结构几何组件基准问题的网格剖分示意图Fig.6 Mesh used in irregular geometric assembly benchmark problem

表3 不规则几何组件基准题计算结果Table 3 Calculation result of irregular geometric assembly benchmark
3 结论
随着新概念堆型的不断提出,其组件设计和堆芯布置不再采用常规的几何形状,传统的基于常规几何的堆芯计算程序已不适用于具有复杂几何的新型反应堆堆芯计算,因此,本文开展了基于任意三角形网格的多群中子扩散数值计算方法研究。首先采用ANSYS软件对计算区域进行三角形网格剖分,利用坐标变换将任意三角形转换为正三角形;其次采用Galerkin变分技术建立包含节块中子平衡方程的泛函,将参量利用正三角形内正交基函数进行展开;最后利用变分原理,获得中子通量密度与节块边界上分中子流的相应关系,并基于源迭代法对其进行求解。基于上述理论模型开发了基于任意三角形网格的变分节块法中子扩散计算程序TriVNM,并采用基准题进行了验证。结果表明,TriVNM具有较高的计算精度,并对复杂几何的新型反应堆具有适用性。

