峰位微扰动修正在构建高斯响应矩阵中的应用研究

赵剑锟，李蔚成，邢义强，吴和喜，张怀强，刘义保

(1.东华理工大学 放射性地质与勘探技术国防重点学科实验室，江西 南昌 330013；2.东华理工大学 核科学与工程学院，江西 南昌 330013)

基于响应矩阵的能谱重建方法广泛应用于γ能谱解析研究，解谱流程为：响应矩阵构建、Gold迭代求解、获取入射谱信息[1-3]。响应矩阵的构建方法主要包括：实测谱法[4-5]、蒙特卡罗模拟法(简称蒙卡法)[6-7]及高斯函数法[7-8]。实测谱法使用过程中需多个标准源，且耗时较长[4-5]，当测量条件发生改变时，需重新测量；蒙卡法无需使用刻度源，但依然无法有效解决峰位漂移的影响[9]；相比以上两种方法，高斯函数法的响应矩阵构建速度更快，在解析低能量分辨率的能谱时表现良好[10]，然而，该方法过度依赖整数道的峰位信息，因此其对高分辨率仪器谱解析能力有待进一步优化[3,11-12]。

随着γ能谱仪能量分辨能力的不断提高(高纯锗能谱仪的道宽可达0.127 keV/道)[13]，特征峰峰形受峰位扰动的影响程度增加。本文拟针对高斯函数法未考虑实测谱峰位处于相邻两道之间而导致解谱中出现杂峰、错峰等问题[11]，通过引入重峰内峰位微扰动修正因子，对高斯响应矩阵进行修正。采用IAEA重峰分解测试谱(G1400)和土壤标准源(TRH1608023)、水样标准源(YMLH1608022)的高纯锗探测器(GMX40P)实测谱对该方法进行解谱能力测试，验证修正方法的有效性。

1 高斯函数法

1.1 高斯函数法解谱原理

根据谱线叠加原理[14]，实测谱形成过程为：

(1)

式中：y(i)为实测谱中第i道计数；x(j)为入射谱第j道计数；Ri,j为入射谱中第j道对第i道的贡献。若考虑本底因素，则有：

y=R·x+ε=

(2)

式中：R为探测器响应矩阵；ε为本底计数。采用直线法扣除本底ε后，R仍为高度病态矩阵，且式(2)中存在统计涨落影响[10,15]。因此，求解x时需使用Gold迭代算法[1]。

1.2 峰位微扰动修正方法

高斯响应矩阵的一般构建方法[11]为：

(3)

式中：σj为标准差；k为道宽，keV/道。

(4)

式中，FWHM为探测器第j道的半高宽，keV。

由半高宽刻度方程得到：

(5)

Ej=kj+d

(6)

式中：a、b均为常数；Ej为第j道所对应的能量；d为拟合直线的截距。

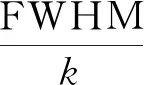
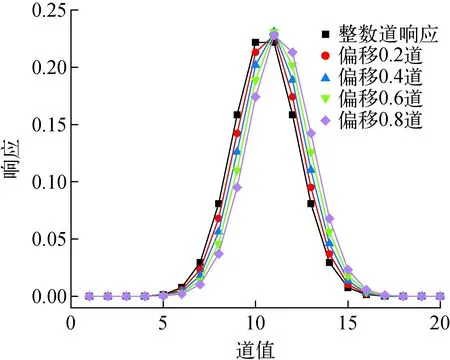
图1 高斯响应示意图Fig.1 Schematic of Gaussian response

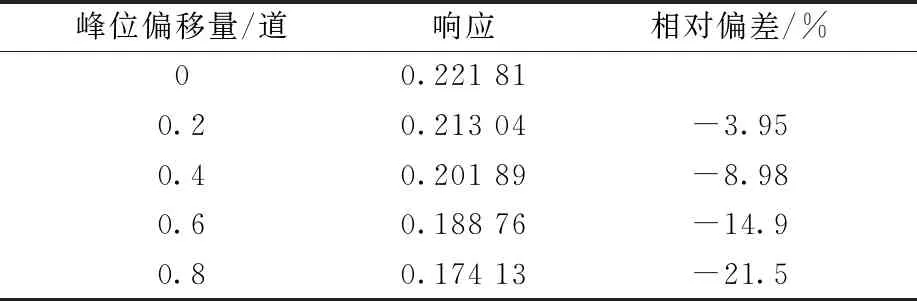
表1 峰位微扰动后高斯响应的相对偏差Table 1 Relative deviation of Gaussian responseby peak position weak variation

由表1可知，当峰位偏移量为0.8道时，峰形响应的相对偏差已达到-21.5%。因此，引入峰位微扰动修正因子cj对响应矩阵进行修正，修正后的高斯响应矩阵为：

(7)

式中，cj为对第j道响应的修正因子。相应地，引入峰位微扰动修正因子后的能量刻度方程为：

农民用水户协会是近年各级党委、政府为配合农村税费改革、减轻农民负担、规范农业水费的收取和管理而提倡成立的一种实行自我管理、民主决策、互助合作的公益性民间组织，是农村专业合作经济组织的组成部分。为进一步提高农民用水户协会管理人员的素质和业务技能,加强协会的队伍建设,提高支斗渠道用水管理水平,巩固和扩大农田水利基本建设成果,提升农业综合生产能力,根据水利部、国家发展改革委和民政部联合印发的《关于加强农民用水户协会建设的意见》，宁夏近年加大贯彻落实力度，按照中央和自治区的要求，对全区农民用水户协会人员和基层水利管理人员进行了培训，取得了较好效果。

Ej=k(j+cj)+d

(8)

1.3 微扰动修正因子的获取

在能量与道值呈线性关系的基础上，以重峰两侧相邻单峰为基准，对重峰区域重新进行能量、半高宽刻度，进而获得微扰动修正因子，具体过程如下。

1) 采用直线法扣除待重建区域的本底。

2) 在单峰处构建微扰动修正响应列矩阵元素为：

(9)

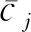
3) 将响应转化为全能峰计数：

(10)

式中：zi为通过响应矩阵计算获得的第i道计数；ymax为实测谱单峰中最大计数；Rmax为列响应矩阵中矩阵元素的最大值。

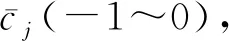
(11)

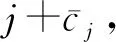
5) 对应重峰区域的微扰动修正因子cj为：

(12)

式中：Ej为重峰内各峰对应的能量；j为Ej对应的整数道值。

2 峰位微扰动修正效果测试

2.1 IAEA标准谱测试

IAEA重峰分解测试谱(G1400)由9个重峰构成，每个重峰包含两个单峰，以道值相差1、3、6，峰面积比1、3、10按顺序排列的G1400重峰分解测试谱示于图2，具体参数列于表2。

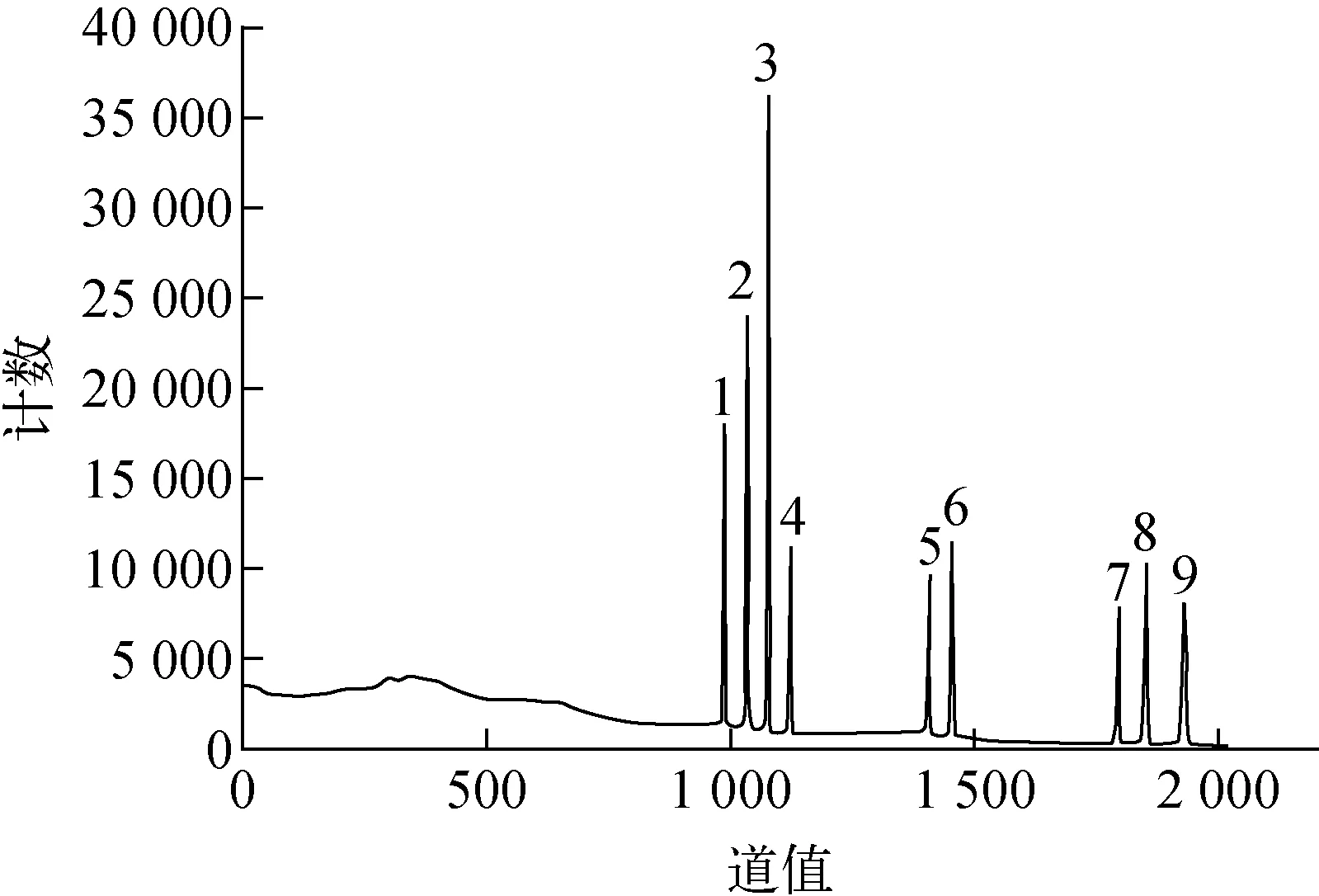
图2 G1400重峰分解测试谱Fig.2 G1400 deconvolution test spectrum

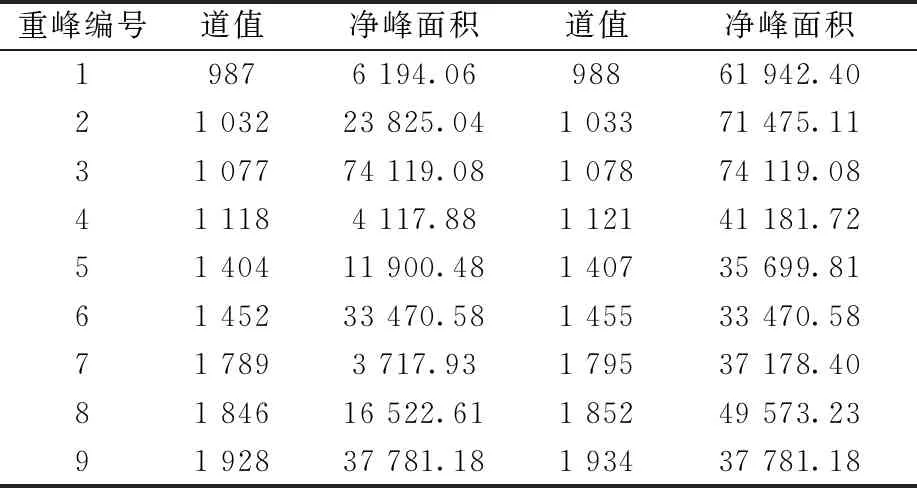
表2 G1400重峰参数Table 2 Overlapped peak parameter of G1400

分别使用高斯响应矩阵(式(3))与修正后的高斯响应矩阵(式(7))对上述9个重峰进行分解，结果示于图3。

由图3可看出，未修正矩阵在重建1～6、9号重峰时出现峰位漂移、无法分解及峰面积计算错误等问题，而引入微扰动修正因子cj后的响应矩阵可将重峰全部准确分解，修正前后各重峰净计数结果列于表3。由表3可知，未修正方法重建结果相对偏差较大，且部分重峰未能有效分解或产生道偏；而修正后结果的相对偏差均在10.25%以内，明显优于未经修正高斯响应矩阵的能谱重建结果。

图3 重建效果对比Fig.3 Comparison of reconstruction result by two response matrices

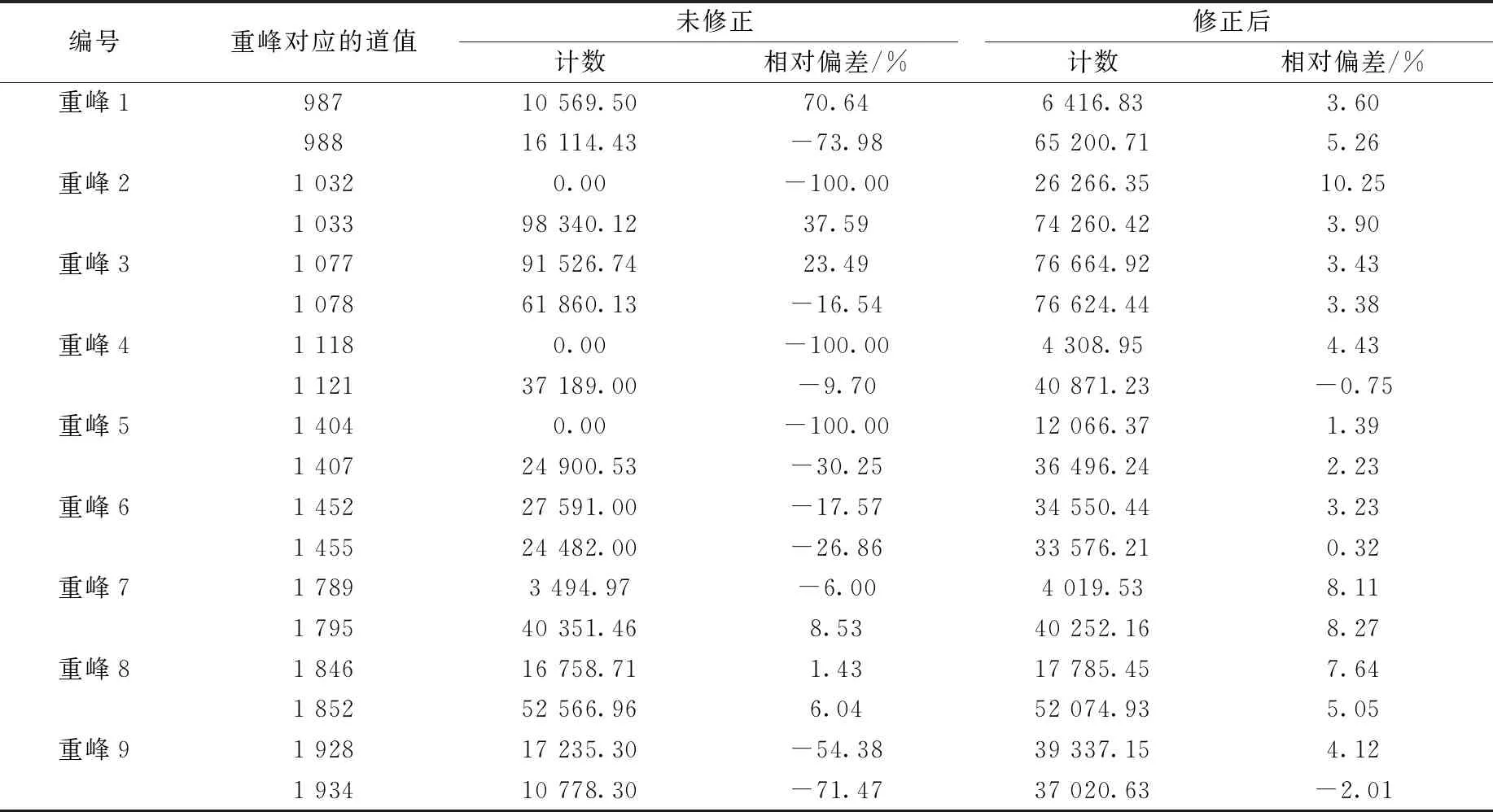
表3 修正前后各重峰净计数对比Table 3 Comparison of net count between revised and original method

2.2 高纯锗实测谱测试

实测谱测试选用高纯锗探测器(GMX40P，能量范围0～2 MeV，8 192道，能量分辨率0.14%@1.332 MeV)对土壤标准源(TRH1608023)、水样标准源(YMLH1608022)进行测量，标准源测量参数列于表4。

表4 标准源测量参数Table 4 Measurement parameter of standard source

选取能谱中235U(185.715 keV)及226Ra(186.211 keV)的重峰进行分解测试，其中，185.715 keV和186.211 keV的衰变分支比分别为57%和3.64%。两射线能量相差0.496 keV，探测效率近似相等。经计算，重峰内两射线峰面积比应分别为5.15∶1和2.67∶1，标准源实测能谱示于图4。

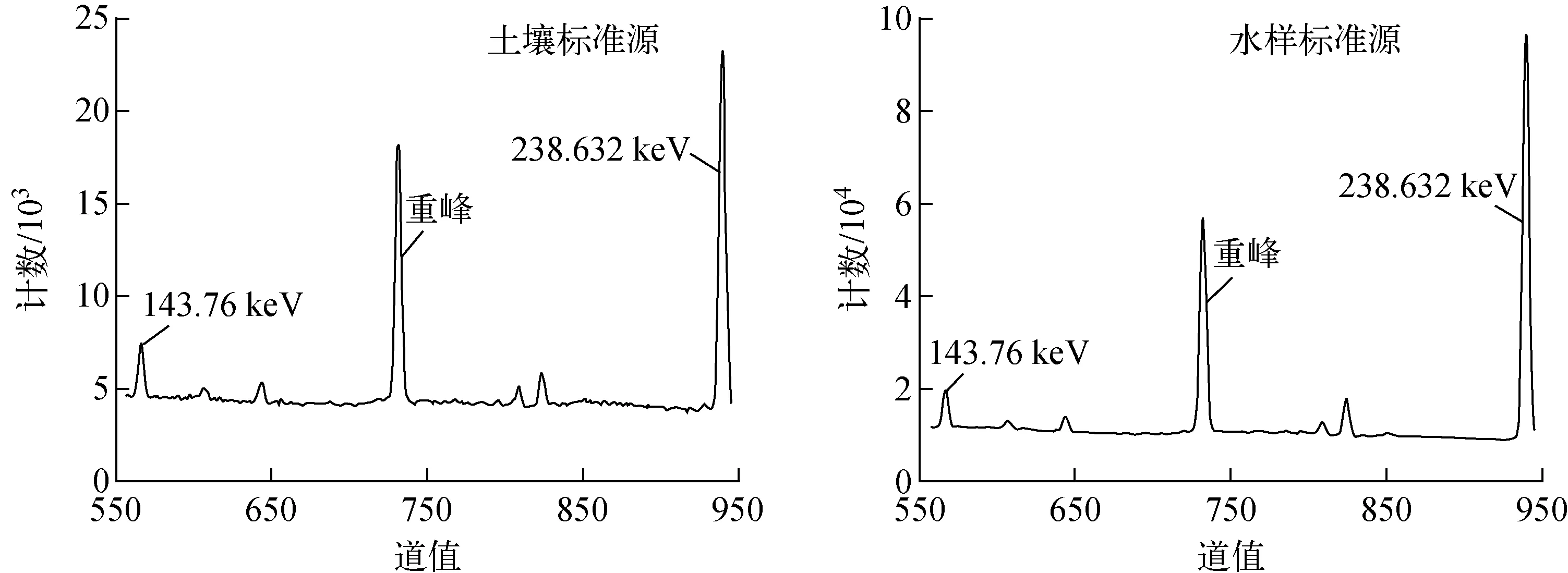
图4 标准源实测能谱Fig.4 Measured spectrum of standard source

使用上述方法求解143.76 keV及238.632 keV全能峰处的标准差及道值，结果列于表5。

表5 全能峰对应道值及标准差Table 5 Channel and standard deviation of full energy peak

将表5中数据代入式(5)、(6)拟合半高宽、能量刻度曲线，结果分别示于图5、6。重峰内各单峰对应半高宽及修正后的道值列于表6，实测谱重建结果示于图7。

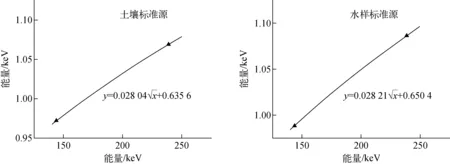
图5 半高宽刻度曲线Fig.5 FWHM calibration curve

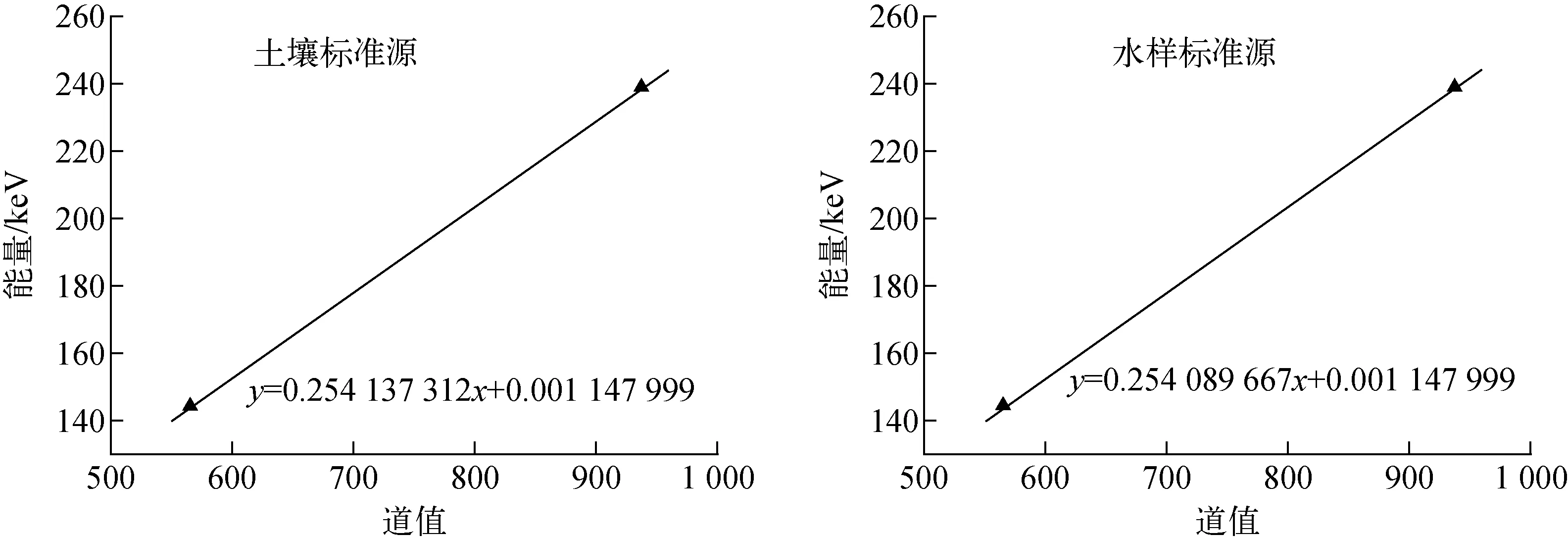
图6 能量刻度曲线Fig.6 Energy calibration curve

图7 实测谱重建结果对比Fig.7 Comparison of measured spectrum reconstruction result

表6 重峰内各单峰对应半高宽及道值Table 6 FWHM and channel of overlapped peak

由图7可见，未修正的高斯响应矩阵未能将土壤标准源中重峰分解；水样标准源重峰经分解后，185.715 keV峰偏1道，186.211 keV峰偏2道，且峰面积的相对偏差分别为17.3%及-34.8%，修正后峰面积计算结果列于表7。由表7可知，修正后的响应矩阵能很好地将重峰分解至对应道值，且净峰面积相对偏差在-5.50%～-0.12%之间。

表7 实测能谱重峰的重建结果Table 7 Reconstruction result of overlapped peak in measured spectrum

3 结论

微扰动修正因子能有效解决现阶段的高斯响应矩阵能谱重建过程中峰位偏移、假峰和峰面积偏差等问题。经IAEA重峰分解测试谱(G1400)和高纯锗实测谱检验，重建能谱的峰位与实际峰位保持一致，峰面积相对偏差分别控制在±10.25%和±5.50%以内。