半漂浮体系钢管混凝土拱桥黏滞阻尼器减震研究

彭益华，何旭辉，敬海泉，严磊

(1.中南大学 土木工程学院，湖南 长沙410075；2.高速铁路建造技术国家工程实验室，湖南 长沙410075；3.广西财经学院，广西 南宁530007)

钢管混凝土拱桥因充分发挥钢材与混凝土2种材料的优势，得到了广泛应用，钢管混凝土拱桥的主梁近年来向连续化和轻型化方向发展[1]。这种新型的拱桥主梁形式恒载小，整体性好[2]，能有效防止单根吊杆断裂导致的桥面坠落，但这种长连续化的轻型主梁结构为释放温差变形引起的结构内力，宜采用半漂浮体系，即主梁的支座只约束主梁横桥向位移，而不约束主梁纵桥向位移。这种半漂浮体系钢管混凝土拱桥在地震作用下的响应不同于传统钢管混凝土拱桥，孙大斌等[3]研究表明半漂浮体系主梁可以显著减小桥墩的地震响应，但拱桥竖直吊杆对主梁纵向位移限制作用有限，半漂浮体系主梁的水平位移较大。因此，需设置阻尼器来控制主梁在地震作用下的位移[4]。在各种耗能阻尼器装置中，黏滞阻尼器因对环境温度和激励频率的变化不敏感，性质比较稳定而得到广泛应用[5−6]，但目前黏滞阻尼器在桥梁中的应用主要集中在漂浮或半漂浮体系斜拉桥[7−10]以及大跨径悬索桥[11]等柔性桥梁中，其研究结果表明：选择适当的黏滞阻尼器参数与设置位置能有效降低地震作用下关键部位的位移与地震力，减隔震效果良好。黏滞阻尼器在拱桥减隔震中的应用相对较晚，广西南宁大桥[12](主跨300 m钢箱拱)在钢箱梁与肋间平台连接的伸缩缝处设置了黏滞阻尼器，以防止地震作用下的碰撞破坏。童申家等[13]研究了拱脚与桥墩间设置黏滞阻尼器对下承式钢管混凝土拱桥的减震效果，结果表明黏滞阻尼器显著降低拱肋轴力响应。周锐等[14]对益阳茅草街大桥(主跨368 m飞鸟式钢管混凝土拱桥)的减震控制研究表明设置黏滞阻尼器对大跨度中承式钢管混凝土拱桥地震响应的总体控制效果要优于设置弹性连接。然而到目前为止，对采用半漂浮式主梁的中承式钢管混凝土拱桥减震研究还较少，有待进一步探讨。本文以某计算跨径252 m的半漂浮体系中承式钢管混凝土拱桥为工程背景，采用非线性动力时程分析法[15]研究了黏滞阻尼器在该类桥中的参数选取方法与减震效果。

1 工程实例

1.1 工程概况与黏滞阻尼器位置选择

如图1所示，高速公路上某特大桥采用中承式钢管混凝土拱桥，计算跨径L=252 m，标准桥面宽33.0 m，矢跨比为1/4，拱肋采用变高度桁式结构，桥面系以上单根拱肋内横向采用缀管连接，桥面系以下单根拱肋内横向采用缀板连接成横哑铃型。主梁为格构式钢-混组合结构，主梁支座布置如图2所示，除主引桥交界墩处的中间支座采用纵桥向单向活动支座外，其余均为双向活动支座，主梁为半漂浮体系。

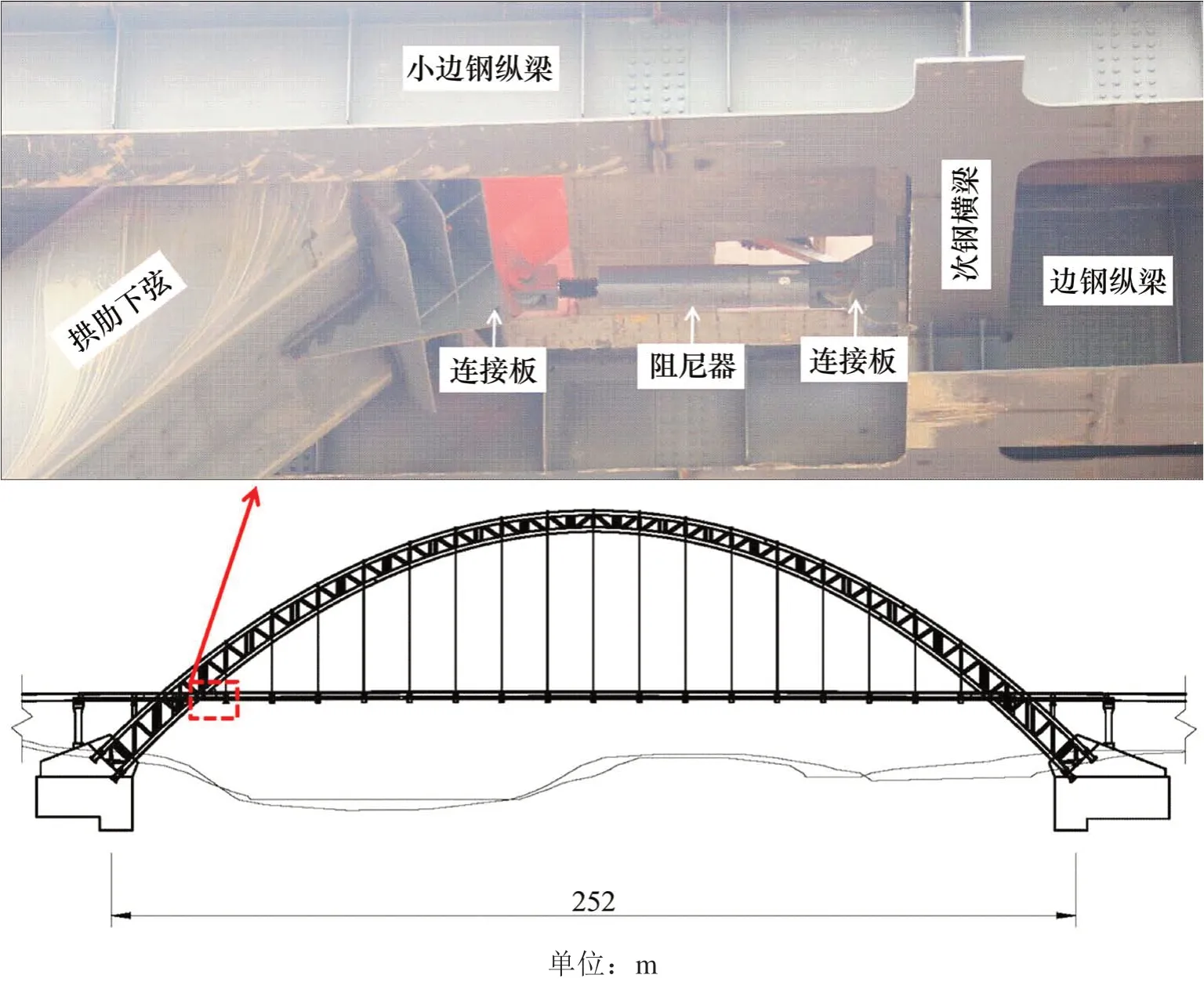
图1 某大跨中承式钢管混凝土拱桥立面布置与黏滞阻尼器位置图Fig.1 Elevation layout and damper location of a large-span half through CFST arch bridge

为控制地震作用下主梁的位移，拟设置黏滞阻尼器进行减震。由于黏滞阻尼器的阻尼力是关于阻尼器活塞运动速度的函数，故黏滞阻尼器最好安装在相对位移较大的位置处[16]，既对减震反应敏感，又具有足够大的滞回耗能所需位移，充分发挥黏滞阻尼器的作用。对中承式钢管混凝土拱桥而言，有2个地方可供选择，一是在交界墩与主梁梁端之间，二是拱肋与主梁之间。本工程由于交界墩较高(约20 m)，纵桥向刚度不够大，在地震作用下可能与桥面主梁一起沿纵桥向振动，不能达到减震的目的，而拱肋刚度大，在地震作用下纵桥向位移小，故最终选择在拱肋与主梁之间设置纵桥向黏滞阻尼器来减震。桥面主梁在拱肋位置处开孔，以确保在地震作用下主梁不能与拱肋碰撞，并在开孔处设置纵向黏滞阻尼器连接主梁与拱肋下弦以控制主梁地震位移，全桥共设置4个，如图2所示。黏滞阻尼器内部构造在文献[7]中已做了详细介绍。

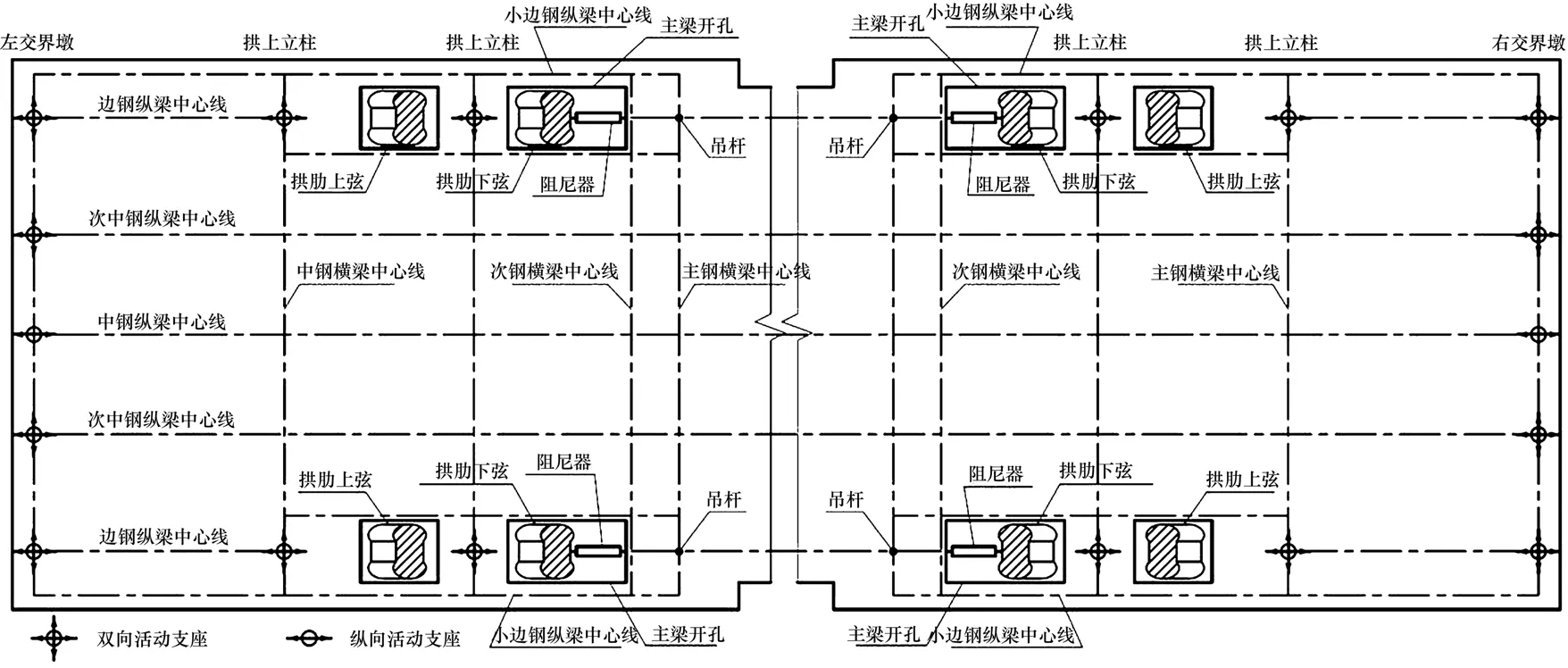
图2 桥梁支座与黏滞阻尼器布置示意图Fig.2 Layout of bridge bearings and dampers

1.2 有限元模型

桥梁空间有限元模型采用大型通用有限元计算软件Midas/Civil建立，如图3所示，拱肋与横撑用梁单元模拟，其中钢管混凝土拱肋采用软件自带的施工阶段联合截面模拟施工过程中的联合刚度与初始应力影响，吊杆用只受拉桁架单元模拟，主梁采用等效主梁模拟，二期恒载通过质量单元施加，所有支座按实际刚度模拟。钢管混凝土拱肋是以受压为主的主要受力构件，不宜依赖于延性设计，故抗震分析不考虑钢管混凝土拱肋材料进入屈服阶段，即不考虑材料非线性，而仅考虑几何非线性与黏滞阻尼器的非线性影响。

图3 桥梁空间有限元模型Fig.3 Spatial finite element model of the bridge

对黏滞阻尼器的模拟常采用简化Maxwell模型[17]，黏滞阻尼器的阻尼力和活塞运动速度之间的关系可表达为：

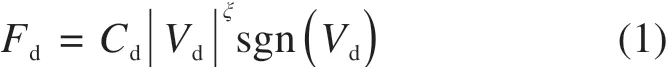
式中：Fd为阻尼力；Cd为阻尼常数；sgn为符号函数；Vd为阻尼器活塞相对阻尼器外壳的运动速度；ξ为阻尼指数，为了抗震需要在实际工程中已经安装的黏滞阻尼器的阻尼指数一般取值集中在0.2～0.4范围[7]，Cd取值较为离散。

1.3 自振特性分析

为了确认桥梁结构减震方案是否合理，采用多重Ritz向量法求解设置黏滞阻尼器前的桥梁结构动力特性，桥梁结构前十阶结构自振频率和振型主要特性如表1所示。前3阶振型均为拱桥主梁的振动，这是由于采用半漂浮体式主梁的钢管混凝土拱桥对主梁的约束较小，因而在自振特性分析中阶次出现的较早，其中第2阶振型为主梁纵飘，振型参与质量达到49%，对纵向振动贡献较大，起主导作用，这与文献[14]的结论一致，可以预见其在地震中的响应对桥梁整体结构的影响也较大，因此本工程拟定的采用黏滞阻尼器来控制桥面主梁纵向位移的减震措施是正确的。

表1 桥梁结构动力特性Table 1 Dynamic characteristics of the bridge

1.4 地震动输入

根据《中国地震动参数区划图》，桥址处工程场地抗震设防烈度为7度，场地类别属Ⅱ类，地震动反应谱特征周期0.35 s，水平向设计基本地震动加速度峰值为0.1g，E2地震加速度峰值为0.17g。根据《公路桥梁抗震设计规范》(JTG/T 2231−01−2020)，设计地震动时程选取与桥址处工程场地特性相近的3条实际地震加速度记录，即El-Centro波、San-fernando波与Tar-Tarzana波，通过调整使其反应谱与设计加速度反应谱匹配，图4给出了调整之后的地震加速度时程，采用纵向+竖向地震组合输入，竖向地震动取水平地震动的2/3[15]，本研究仅考察一致激励地震作用下的结构响应，桥梁的阻尼采用瑞利阻尼，结构阻尼比取为0.05[19]。采用Newmark直接积分算法，时间步长为0.02 s，从图4可以看出加速度较大的地震动主要集中在前30 s，因此计算总时间取为30 s。时程分析的最终结果，取3组地震波计算结果的最大值。

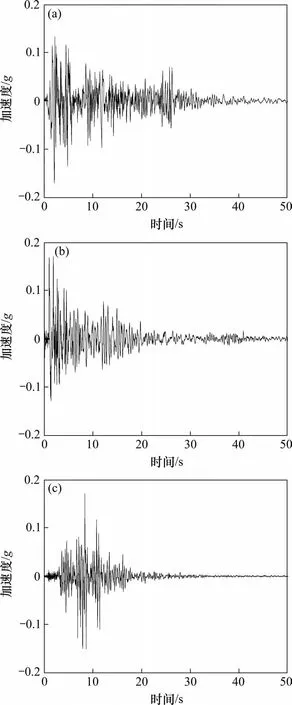
图4 地震波加速度时程Fig.4 Acceleration time history of seismic wave

1.5 黏滞阻尼器参数选取研究

黏滞阻尼器参数主要是指阻尼系数Cd与阻尼指数ξ，一般通过关键控制因素的参数分析择优选取[18]。对半漂浮式主梁钢管混凝土拱桥而言，黏滞阻尼器的主要目的是控制主梁地震位移，同时需关注阻尼力对相关连接构件的影响，使其在容许承受的荷载范围内。同时满足各类控制因素要求的阻尼器参数范围为最终选择黏滞阻尼器参数的可选范围，经分析比较后发现纵向位移控制值是梁端纵向位移容许值，为35 mm；而内力控制值为黏滞阻尼器连接件所能承受的阻尼力，为1 000 kN。

为了研究得到满足控制因素要求的黏滞阻尼器参数，需要进行一系列的参数分析，参考已经在工程中实际使用的黏滞阻尼器参数[7,12−14]，将黏滞阻尼器阻尼系数试算范围取为500～4 000，阻尼指数ξ试算范围取为0.2，0.25，0.3以及0.35。经有限元计算分析，可以得到在地震波历时范围内的桥梁结构内力与位移响应时程，而控制结构设计的往往是最大值或最小值，因此需要重点关注内力与位移响应时程的绝对值最大值。将各试算工况的计算结果汇总如图5和图6所示。

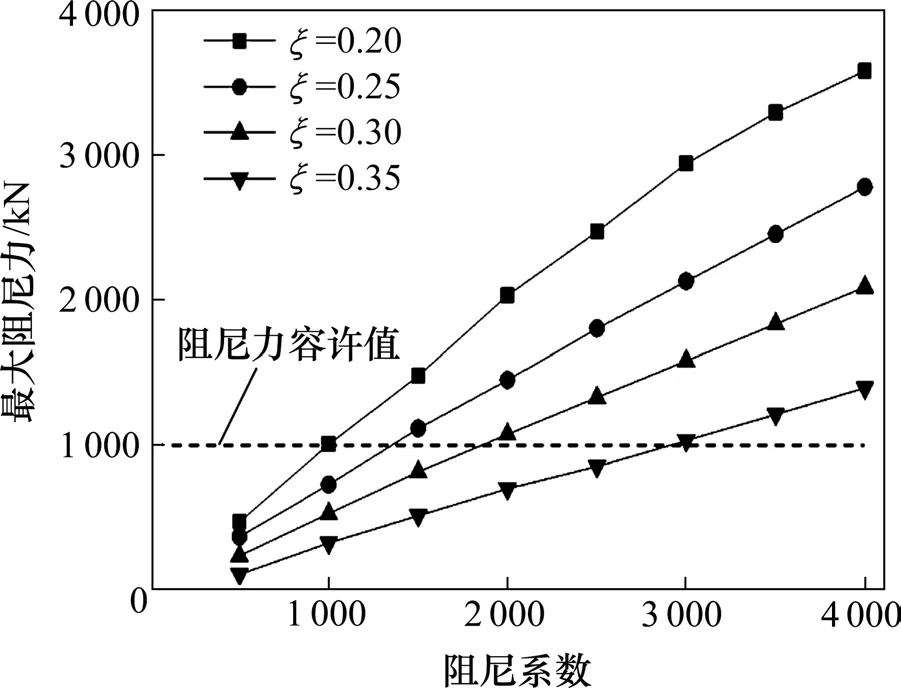
图6 阻尼系数与阻尼指数对阻尼力的影响Fig.6 Influence of damping coefficient and damping index on damping force

从图5可以看出，梁端最大纵向位移响应随着阻尼系数与阻尼指数的变化而变化，对相同的阻尼指数，梁端最大纵向位移响应随着阻尼系数的增大呈非线性减小，并收敛于约11.7 mm，这是由于阻尼系数很大时，接近主梁与拱肋固结的情形，故梁端最大纵向位移响应不再随阻尼系数而变化。对相同的阻尼系数，梁端最大纵向位移响应随着阻尼指数的增大而增大。图中虚线所示为梁端纵向位移容许值，虚线下方各曲线取值为满足纵向位移要求的阻尼系数与阻尼指数。

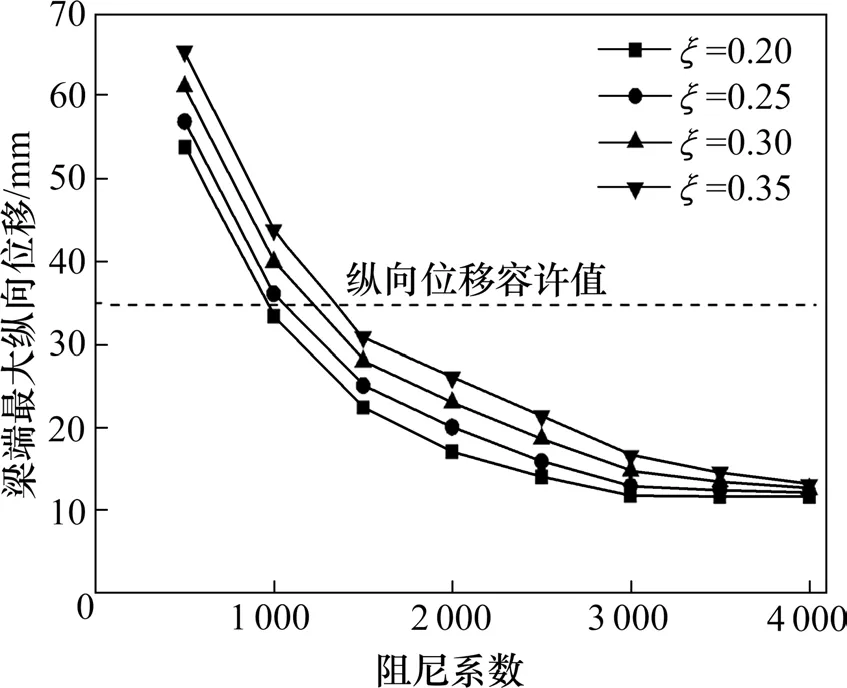
图5 阻尼系数与阻尼指数对梁端纵向位移响应的影响Fig.5 Influence of damping coefficient and damping index on longitudinal displacement of the beam end

从图6可以看出，最大阻尼力响应也随着阻尼系数与阻尼指数的变化而变化，对相同的阻尼指数，最大阻尼力响应随着阻尼系数的增大基本呈线性增大，对相同的阻尼系数，最大阻尼力响应随着阻尼指数的增大而减小。图中虚线所示为阻尼力容许值，虚线下方各曲线取值为满足阻尼力要求的阻尼系数与阻尼指数。

显然，同时满足梁端纵向位移要求与最大阻尼力要求的阻尼系数与阻尼指数为两图中虚线下方各参数的交集，综合图5与图6可得到与阻尼指数对应的阻尼系数选取范围，如表2所示。此外，黏滞阻尼器滞回曲线面积越大耗能能力越强，应选择滞回曲线尽量饱满的黏滞阻尼器，同时结合黏滞阻尼器生产商的产品规格序列，最终选定用于该桥梁的黏滞阻尼器指数ξ=0.3，阻尼系数Cd=1 400，即阻尼器阻尼力Fd=1400⋅V0.3d。

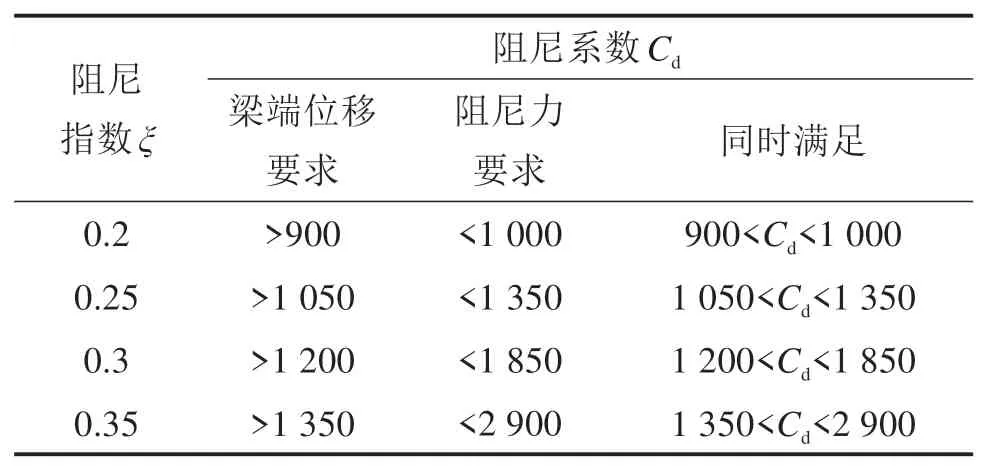
表2 阻尼系数与阻尼指数选取Table 2 Damping coefficient and damping index selection

1.6 黏滞阻尼器减震效果分析

1.6.1 地震位移响应对比分析

通过计算分析，可以得到在地震作用下阻尼器设置前后关键部位(本文选取梁端纵向位移、拱顶纵向与竖向位移)的位移时程，图7和图8示出了设置阻尼器前后，地震作用下梁端纵向位移响应时程对比，同理也可以得到其他位移响应时程对比，由于绝对值最大值往往是控制设计的因素，提取位移响应时程中的绝对值最大值，汇总如表3所示。为简化表述，下文中各位移值均指位移响应时程最大值。

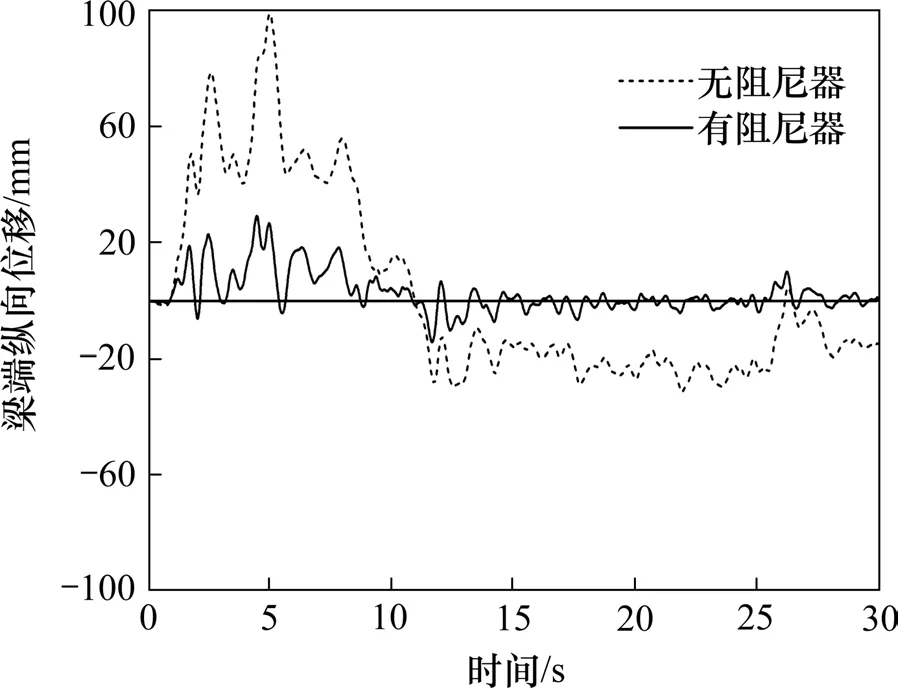
图7 设置阻尼器前后梁端纵向位移时程比较Fig.7 Time history comparison of longitudinal displacement of beam end before and after installing dampers

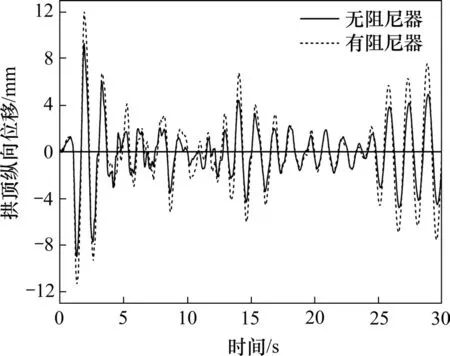
图8 设置阻尼器前后拱顶纵向位移时程比较Fig.8 Time history comparison of longitudinal displacement of arch crown before and after installing dampers

表3 关键位置的最大位移响应比较Table 3 Comparison of maximum displacement responses at key locations

由图7和图8以及表3可见，设置黏滞阻尼器前，梁端最大纵向位移响应约99.2 mm，远超过梁端纵向位移容许值35 mm，设置阻尼器以后，梁端纵向位移响应最大值为29.3 mm，小于梁端容许位移限值，梁端纵向位移响应减少了约70%，这非常有利于避免地震作用下伸缩缝破坏与梁端碰撞。拱顶纵向位移增大了29%，这是由于拱肋承受了阻尼器传递过来的主梁地震力所致，拱顶竖向位移减少了7.5%，由于拱肋刚度较大，拱顶位移响应的绝对值变化并不大。

1.6.2 地震内力响应对比分析

同理，通过动力时程分析可以得到阻尼器阻尼力以及阻尼器设置前后的拱肋关键部位(本文选取拱脚、阻尼器位置处、L/4处与拱顶)的内力响应时程曲线。计算得到地震过程中的最大阻尼力为745 kN，小于容许值1 000 kN，满足阻尼器选取要求。图9示出了设置黏滞阻尼器前后，地震作用下阻尼器位置处拱肋下弦弯矩响应时程对比，同理也可以得到其他内力响应时程对比，由于控制设计的往往是地震内力响应最大值，因此提取地震内力响应时程中的最大值(轴力以拉为正，以压为负，地震内力与恒载内力组合时，地震轴压力更为不利，故仅比较轴压力)，汇总如表4所示。为简化表述，下文中各内力值均指地震内力响应时程最大值。

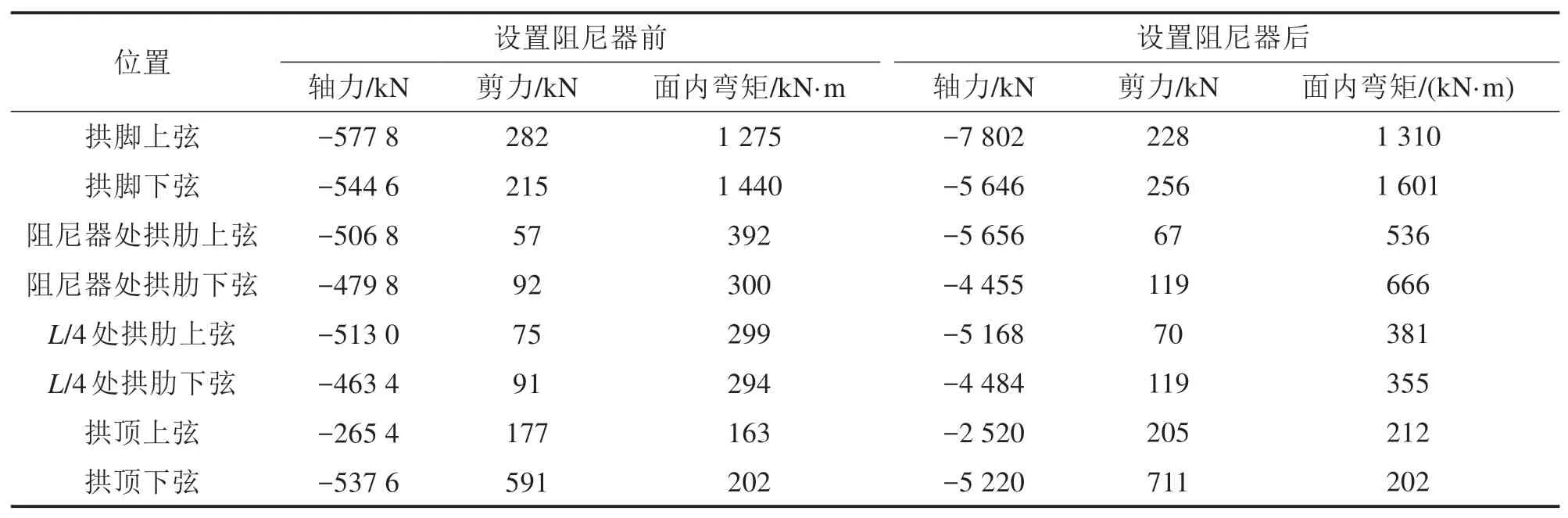
表4 关键截面内力最大响应比较Table 4 Comparison of maximum response of internal forces at key sections

图9 设置阻尼器前后阻尼器位置处拱肋下弦弯矩时程Fig.9 Time history comparison of moment of arch bottom chord at damper position before and after installing dampers

可见，设置黏滞阻尼器以后，地震作用下，在阻尼器位置以下拱肋轴压力有所增加(约4%～35%)，而阻尼器位置以上拱肋轴压力有所减少(约3%～7%)，其中，拱脚上弦轴力增加约35%，拱顶上弦轴力减少约5%。除拱脚与L/4(L为跨径)处上弦外，其他各处剪力响应增大了15%～30%。各处弯矩响应均有所增大，设置阻尼器处拱肋下弦弯矩增大了122%，其他各处弯矩响应增大了0%～37%，这说明设置黏滞阻尼器对阻尼器处拱肋弯矩响应的影响大于其他各处拱肋，但由于拱肋刚度较大，经计算，在设置阻尼器情况下，地震引起的阻尼器处拱肋下弦弯曲应力仅为4.88 MPa，应力绝对值仍较小。

1.6.3 不同地震波计算结果离散性分析

表5 示出了不同地震波的动力时程分析结果，3组地震波时程分析结果所得规律基本一致，各组地震波计算所得内力或位移最小值与最大值相差均在15%以内。

表5 不同地震波计算结果离散性分析Table 5 Dispersion analysis of calculation results under different seismic waves

2 结论

1)以梁端容许位移与阻尼器连接件所能承受的最大阻尼力作为控制因素，通过参数分析得到满足减震需求的黏滞阻尼器参数的方法是可取的。

2)设置合适的阻尼器以后，能显著减小梁端位移(工程实例减少约70%)，同时也导致拱顶纵向位移有所增加，但由于拱肋整体刚度较大，拱顶纵向位移响应绝对值依然较小，仅12.0 mm。

3)设置阻尼器以后，对拱肋各关键位置处的轴力、剪力、弯矩响应的影响规律不尽相同，在设置阻尼器位置以下拱肋轴力有所增加(约4%～35%)，而阻尼器位置以上拱肋轴力有所减少(约3%～7%)，除拱脚与L/4(L为跨径)处上弦外，其他各处剪力响应增大了15%～30%，对阻尼器位置处的拱肋下弦弯矩响应影响(增大约122%)大于其他各处拱肋。